Термин «корреляция» активно используется в гуманитарных науках, медицине; часто мелькает в СМИ. Ключевую роль корреляции играют в психологии. В частности, расчет корреляций выступает важным этапом реализации эмпирического исследования при написании ВКР по психологии.
Материалы по корреляциям в сети слишком научны. Неспециалисту трудно разобраться в формулах. В то же время понимание смысла корреляций необходимо маркетологу, социологу, медику, психологу – всем, кто проводит исследования на людях.
В этой статье мы простым языком объясним суть корреляционной связи, виды корреляций, способы расчета, особенности использования корреляции в психологических исследованиях, а также при написании дипломных работ по психологии.
- Прямая и обратная корреляция
- Сильная и слабая корреляция
- Расчет корреляций с помощью электронных таблиц Microsoft Excel
- Как вычислить значение корреляции с помощью статистической программы STATISTICA
Что такое корреляция
Корреляция – это связь. Но не любая. В чем же ее особенность? Рассмотрим на примере.
КОРРЕЛЯЦИЯ Спирмена Пирсона STATISTICA #08
Представьте, что вы едете на автомобиле. Вы нажимаете педаль газа – машина едет быстрее. Вы сбавляете газ – авто замедляет ход. Даже не знакомый с устройством автомобиля человек скажет: «Между педалью газа и скоростью машины есть прямая связь: чем сильнее нажата педаль, тем скорость выше».
Это зависимость функциональная – скорость выступает прямой функцией педали газа. Специалист объяснит, что педаль управляет подачей топлива в цилиндры, где происходит сжигание смеси, что ведет к повышению мощности на вал и т.д. Это связь жесткая, детерминированная, не допускающая исключений (при условии, что машина исправна).
Теперь представьте, что вы директор фирмы, сотрудники которой продают товары. Вы решаете повысить продажи за счет повышения окладов работников. Вы повышаете зарплату на 10%, и продажи в среднем по фирме растут. Через время повышаете еще на 10%, и опять рост. Затем еще на 5%, и опять есть эффект.
Напрашивается вывод – между продажами фирмы и окладом сотрудников есть прямая зависимость – чем выше оклады, тем выше продажи организации. Такая же это связь, как между педалью газа и скоростью авто? В чем ключевое отличие?
Правильно, между окладом и продажами заисимость не жесткая. Это значит, что у кого-то из сотрудников продажи могли даже снизиться, невзирая на рост оклада. У кого-то остаться неизменными. Но в среднем по фирме продажи выросли, и мы говорим – связь продаж и оклада сотрудников есть, и она корреляционная.
В основе функциональной связи (педаль газа – скорость) лежит физический закон. В основе корреляционной связи (продажи – оклад) находится простая согласованность изменения двух показателей. Никакого закона (в физическом понимании этого слова) за корреляцией нет. Есть лишь вероятностная (стохастическая) закономерность.
Численное выражение корреляционной зависимости
Итак, корреляционная связь отражает зависимость между явлениями. Если эти явления можно измерить, то она получает численное выражение.
КОРРЕЛЯЦИЯ Спирмена Пирсона Кенделла | АНАЛИЗ ДАННЫХ #12
Например, изучается роль чтения в жизни людей. Исследователи взяли группу из 40 человек и измерили у каждого испытуемого два показателя: 1) сколько времени он читает в неделю; 2) в какой мере он считает себя благополучным (по шкале от 1 до 10). Ученые занесли эти данные в два столбика и с помощью статистической программы рассчитали корреляцию между чтением и благополучием.
Предположим, они получили следующий результат -0,76. Но что значит это число? Как его проинтерпретировать? Давайте разбираться.
Полученное число называется коэффициентом корреляции. Для его правильной интерпретации важно учитывать следующее:
- Знак «+» или «-» отражает направление зависимости.
- Величина коэффициента отражает силу зависимости.
Прямая и обратная
Знак плюс перед коэффициентом указывает на то, что связь между явлениями или показателями прямая. То есть, чем больше один показатель, тем больше и другой. Выше оклад — выше продажи. Такая корреляция называется прямой, или положительной.
Если коэффициент имеет знак минус, значит, корреляция обратная, или отрицательная. В этом случае чем выше один показатель, тем ниже другой. В примере с чтением и благополучием мы получили -0,76, и это значит, что, чем больше люди читают, тем ниже уровень их благополучия.
Сильная и слабая
Корреляционная связь в численном выражении – это число в диапазоне от -1 до +1. Обозначается буквой «r». Чем выше число (без учета знака), тем корреляционная связь сильнее.
Чем ниже численное значение коэффициента, тем взаимосвязь между явлениями и показателями меньше.
Максимально возможная сила зависимости – это 1 или -1. Как это понять и представить?
Рассмотрим пример. Взяли 10 студентов и измерили у них уровень интеллекта (IQ) и успеваемость за семестр. Расположили эти данные в виде двух столбцов.
Испытуемый
IQ
Успеваемость (баллы)
Посмотрите внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. Но также растет и уровень успеваемости. Из любых двух студентов успеваемость будет выше у того, у кого выше IQ. И никаких исключений из этого правила не будет.
Перед нами пример полного, 100%-но согласованного изменения двух показателей в группе. И это пример максимально возможной положительной взаимосвязи. То есть, корреляционная зависимость между интеллектом и успеваемостью равна 1.
Рассмотрим другой пример. У этих же 10-ти студентов с помощью опроса оценили, в какой мере они ощущают себя успешными в общении с противоположным полом (по шкале от 1 до 10).
Испытуемый
IQ
Успех в общении с противоположным полом (баллы)
Смотрим внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. При этом в последнем столбце последовательно снижается уровень успешности общения с противоположным полом. Из любых двух студентов успех общения с противоположным полом будет выше у того, у кого IQ ниже. И никаких исключений из этого правила не будет.
Это пример полной согласованности изменения двух показателей в группе — максимально возможная отрицательная взаимосвязь. Корреляционная связь между IQ и успешностью общения с противоположным полом равна -1.
А как понять смысл корреляции равной нулю (0)? Это значит, связи между показателями нет. Еще раз вернемся к нашим студентам и рассмотрим еще один измеренный у них показатель – длину прыжка с места.
Испытуемый
IQ
Длина прыжка с места (м)
Не наблюдается никакой согласованности между изменением IQ от человека к человеку и длинной прыжка. Это и свидетельствует об отсутствии корреляции. Коэффициент корреляции IQ и длины прыжка с места у студентов равен 0.
Корреляционный анализ в системе Statistica

Значимость частных коэффициентов корреляции проверяется по тем же критериям, что и парных. То есть находят наблюдаемое значение t-критерия:
, где r – оценка частного коэффициента корреляции;
l – число фиксируемых факторов.
Проверяемый коэффициент корреляции считается значимым если tнабл. по модулю будет больше чем tкр, определяемое по таблице t-распределения для заданного α и v=n-l-2.
Множественный коэффициент корреляции характеризует тесноту связи между результативной переменной и независимыми. Он изменяется в пределах от 0 до 1 и рассчитывается по формуле:
, где │R│ — определитель корреляционной матрицы;
Rjj — алгебраическое дополнение jj-го элемента.
В случае двух объясняющих переменных формула для вычисления множественного коэффициента детерминации имеет вид:
Квадрат множественного коэффициента корреляции называется множественным коэффициентом детерминации. Он показывает, какая доля дисперсии результативного признака объясняется влиянием независимых переменных.
Значимость множественного коэффициента корреляции проверяется по F-критерию.
Наблюдаемое значение находится по формуле:
Множественный коэффициент корреляции считается значимым, т.е. имеет место статистическая зависимость между Y и остальными факторами X, если Fнабл. > Fкр. (α, k-1, n-k), где Fкр. определяется по таблице F-распределения.
Показателям тесноты связи можно дать качественную оценку на основе шкалы Чеддока:
Количественная мера
тесноты связи (по модулю)
Качественная характеристика
слабая
умеренная
заметная
высокая
весьма высокая
Заметим, что функциональная связь возникает при значении равном 1, а отсутствие связи — 0. При значениях показателей тесноты связи меньше 0,7 величина коэффициента детерминации всегда будет ниже 50%. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение.
Основные этапы проведения корреляционного анализа в системе рассмотрим на данных Примера 1. Исходные данные представляют собой результаты наблюдений за деятельностью 23 предприятий одной из отраслей промышленности.
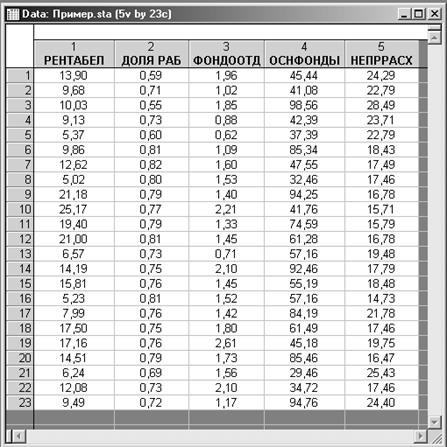
Графы таблицы содержат следующие показатели:
ДОЛЯ РАБ – удельный вес рабочих в составе ППП, ед.;
ФОНДООТД – фондоотдача, ед.;
ОСНФОНДЫ – среднегодовая стоимость основных производственных фондов, млн. руб.;
НЕПРРАСХ – непроизводственные расходы, тыс. руб.
Требуется исследовать зависимость рентабельности от других показателей.
Предположим, что рассматриваемые признаки в генеральной совокупности подчиняются нормальному закону распределения, а данные наблюдений представляют собой выборку из этой совокупности.
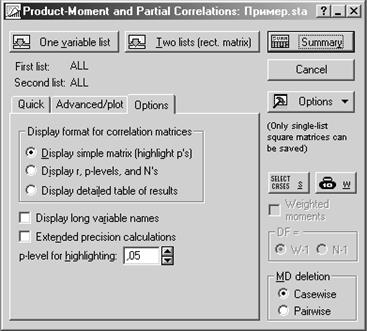
Шаг 1. Вычислим парные коэффициенты корреляции между всеми переменными (Basic Statistics and Tables / Correlation matrices). Обратите внимание на закладку Options (Опции) в появившемся диалоговом окне.
один список (квадратная) / два списка (прямоугольная)
отображать простую матрицу
отображать уровень значимости, количество и r
отображать подробную таблицу результатов
отображать длинные имена переменных
вычисления с повышенной точностью
уровень значимости (p-level)
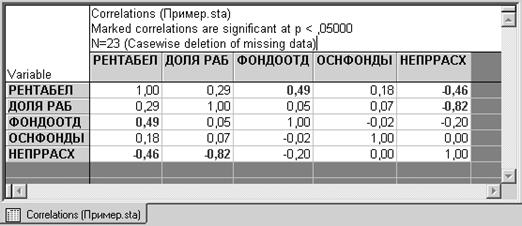
Шаг 2. В нашем примере показатель рентабельности оказался наиболее связан с показателями (выделены красным цветом):
фондоотдача (связь прямая)
и непроизводственные расходы (обратная связь).
При дальнейшем построении уравнения регрессии следует ограничиться именно этими показателями как наиболее информативными.
Однако в нашем примере наблюдается явление мультиколлениарности, когда существует связь между самими независимыми переменными (парный коэффициент корреляции по модулю больше, чем 0,8). В нашем примере между непроизводственными расходами и показателем доли рабочих в составе ППП парный коэффициент равен –0,82. Чаще всего устранение мультиколлениарности решается путем исключения из дальнейшего анализа одной из таких переменных. Очевидно, в нашем случае следует удалить показатель доли рабочих
Источник: vunivere.ru
Расчет коэффициента корреляции в SPSS
Для того, чтобы рассчитать коэффициент корреляции используя статистический пакет SPSS необходимо сделать следующие шаги:
1.Вносим значения для двух переменных в таблицу Data Editor. (Например var1 и var2)
2. Выбираем Analyze -> Correlate -> Bivariate…
3. В открывшемся окне выделяем две переменные (например var1 и var2).
4. Нажимаем на кнопку >. Выделенные переменные перенесутся вправо, в окно Paired Variables (они будут выглядеть как var1-var2).
- корреляцию Пирсона (Pearson) — стоит по-умолчанию
- корреляцию r-Спирмена (Spearman)
- корреляцию t-Кендала (Kendal)
5.1.Если необходимо учесть пропуски значений путем их построчного удаления, то нажимаем Options -> Exclude cases listwise -> Continue. По-умолчанию программа использует учет пропусков значений путем их попарного удаления (Exclude cases pairwise).
6. Нажимаем Ок
7. Смотрим полученный результат
Источник: statpsy.ru