т.е. как отношение времени решения задач на скалярной ЭВМ к времени выполнения параллельного алгоритма (величина n применяется для параметризации вычислительной сложности решаемой задачи и может пониматься, например, как количество входных данных задачи).
Эффективность ( efficiency ) использования параллельным алгоритмом процессоров при решении задачи определяется соотношением
Ep(n)=T1(n)/(pTp(n))=Sp(n)/p
(величина эффективности определяет среднюю долю времени выполнения алгоритма, в течение которой процессоры реально задействованы для решения задачи).
Из приведенных соотношений можно показать, что в наилучшем случае Sp(n)=p и Ep(n)=1 . При практическом применении данных показателей для оценки эффективности параллельных вычислений следует учитывать два важных момента:
- При определенных обстоятельствах ускорение может оказаться больше числа используемых процессоров Sp(n)>p — в этом случае говорят о существовании сверхлинейного (superlinear) ускорения. Несмотря на парадоксальность таких ситуаций ( ускорение превышает число процессоров), на практике сверхлинейное ускорение может иметь место. Одной из причин такого явления может быть неодинаковость условий выполнения последовательной и параллельной программ. Например, при решении задачи на одном процессоре оказывается недостаточно оперативной памяти для хранения всех обрабатываемых данных и тогда становится необходимым использование более медленной внешней памяти (в случае же использования нескольких процессоров оперативной памяти может оказаться достаточно за счет разделения данных между процессорами). Еще одной причиной сверхлинейного ускорения может быть нелинейный характер зависимости сложности решения задачи от объема обрабатываемых данных. Так, например, известный алгоритм пузырьковой сортировки характеризуется квадратичной зависимостью количества необходимых операций от числа упорядочиваемых данных. Как результат, при распределении сортируемого массива между процессорами может быть получено ускорение , превышающее число процессоров (более подробно данный пример рассматривается в «Параллельные методы сортировки» ). Источником сверхлинейного ускорения может быть и различие вычислительных схем последовательного и параллельного методов,
- При внимательном рассмотрении можно обратить внимание, что попытки повышения качества параллельных вычислений по одному из показателей (ускорению или эффективности) могут привести к ухудшению ситуации по другому показателю, ибо показатели качества параллельных вычислений являются часто противоречивыми. Так, например, повышение ускорения обычно может быть обеспечено за счет увеличения числа процессоров, что приводит, как правило, к падению эффективности. И наоборот, повышение эффективности достигается во многих случаях при уменьшении числа процессоров (в предельном случае идеальная эффективность Ep(n)=1 легко обеспечивается при использовании одного процессора). Как результат, разработка методов параллельных вычислений часто предполагает выбор некоторого компромиссного варианта с учетом желаемых показателей ускорения и эффективности.
При выборе надлежащего параллельного способа решения задачи может оказаться полезной оценка стоимости (cost) вычислений, определяемой как произведение времени параллельного решения задачи и числа используемых процессоров
Отладка параллельных программ на Go. Андрей Солдатенко
Воеводин В. В. — Суперкомпьютеры — Характеристики параллельных программ
Cp=pTp.
В связи с этим можно определить понятие стоимостно-оптимального (cost-optimal) параллельного алгоритма как метода, стоимость которого является пропорциональной времени выполнения наилучшего последовательного алгоритма.
Далее для иллюстрации введенных понятий в следующем пункте будет рассмотрен учебный пример решения задачи вычисления частных сумм для последовательности числовых значений. Кроме того, данные показатели будут использоваться для характеристики эффективности всех рассматриваемых в лекциях 6 – 11 параллельных алгоритмов при решении ряда типовых задач вычислительной математики.
2.5. Учебный пример. Вычисление частных сумм последовательности числовых значений
Рассмотрим для демонстрации ряда проблем, возникающих при разработке параллельных методов вычислений, сравнительно простую задачу нахождения частных сумм последовательности числовых значений
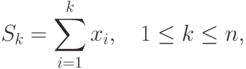
где n есть количество суммируемых значений (данная задача известна также под названием prefix sum problem ).
Изучение возможных параллельных методов решения данной задачи начнем с еще более простого варианта ее постановки – с задачи вычисления общей суммы имеющегося набора значений (в таком виде задача суммирования является частным случаем общей задачи редукции )
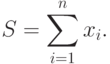
2.5.1. Последовательный алгоритм суммирования
Традиционный алгоритм для решения этой задачи состоит в последовательном суммировании элементов числового набора
S=0, S=S+x1.
Вычислительная схема данного алгоритма может быть представлена следующим образом (см. рис. 2.2):
G1=(V1,R1),
Источник: intuit.ru
Характеристики параллельности (ускорение, эффективность, стоимость и ценность параллельного решения).

Характеристики параллельности Ускорение параллельного вычисления ξ = T 1 (n) /T р (n) Чем менее связная задача, тем больше число подсистем на которые целесообразно разбивать исходные подзадачи. Чем более связная задача, тем меньше число подсистем р на которые следует разбивать исходные подзадачи. Чем ближе значение ускорения к р ( ξ→ р) , тем лучше параллельный алгоритм и соответствующая параллельная программа Эффективность параллельного вычисления ξ * = ξ /р=T 1 (n) /(T р (n)*р) Чем ближе значение ускорения к р, тем более эффективен ( ξ * → 1) параллельный алгоритм и соответствующая параллельная программа Цена параллельного решения C p = p*T p (n) Ценность параллельного решения F p = ξ /C p = T 1 (n)/p*T p 2 (n). Иллюстрация приведенных характеристик на примере решения СЛАУ большой размерности путем декомпозиции на подзадачи меньших размеров ξ
Р/lnP -теория сложности
log 2 P -гипотеза Минского р Эффективность параллельных вычислений ξ * = ξ /р → 1, т.к. ξ → р.
(Реально 0.5-0.7)
Пример:
р – число вычислителей и число
Чем менее связная задача, тем больше число подсистем, на которые целесообразно разбивать исходные подзадачи. Чем более связная задача, тем меньше число подсистем р на которые следует разбивать исходные подзадачи.
ξ * 1  α ~10 -4 α ~ 10 -3 0.5 α ~10 -2
α ~10 -4 α ~ 10 -3 0.5 α ~10 -2  p
p
| 2 | 10 | 100 | 1000 |
ξ * = T 1 (n) /(T р (n)*р)
Закон Амдаля и его следствия
Используется для оценки параллельных алгоритмов, структура которых предполагает выполнение всех операций либо с максимальной, либо с минимальной степенью параллелизма, время на подготовку передачи данных отсутствует. Например, для структуры изображенной ниже, где минимальная степень =1, максимальная =3, можно использовать оценку ускорения по закону Амдаля.
Определим ускорение параллельного алгоритма исходя из анализа частей алгоритма, выполняемых последовательно и параллельно: Предположим, что программе доля операций, которые нужно выполнять последовательно, равна β, где 0 <= β <=1 (при этом доля понимается не по статическому числу строк кода, а по числу операций в процессе выполнения). Крайние случаи в значениях β соответствуют полностью параллельным (β =0) и полностью последовательным (β =1) программам. Чтобы оценить, какое ускорение S может быть получено на компьютере из p процессоров при данном значении β, можно воспользоваться законом Амдала:
| S = | T 1 ( n ) | , где t доп – время на накладные расходы | ||
| ( β + | 1 − β | ) T | ( n ) + t | |
| доп | ||||
| p | 1 | |||
β — доля операций, выполнение которых невозможно одновременно с другими операциями. Проанализируем полученное соотношение: 1. Если β =0, t доп =0, тогда S=p (т.е. алгоритм полностью параллелен, отсутствует последовательная часть)
| 2. | Если β <>0, t доп =0, тогда S = | 1 | — Закон Амдаля | |||||
| ( β + | 1 | − β | ) | |||||
| p | ||||||||
| 3. | Если β – любое, t доп >>0, тогда S = | T 1 ( n ) | < 1 , | |||||
| t доп | ||||||||
Имеем большие затраты на обмен данными и синхронизацию, что может привести к неэффективности параллельного алгоритма. Если 9/10 программы исполняется параллельно, а 1/10 по-прежнему последовательно, то ускорения более, чем в 10 раз получить в принципе невозможно вне зависимости от качества реализации параллельной части кода и числа используемых процессоров (ясно, что 10 получается только в том случае, когда время исполнения параллельной части равно 0). Посмотрим на проблему с другой стороны: а какую же часть кода надо ускорить (а значит и предварительно исследовать), чтобы получить заданное ускорение? Ответ можно найти в следствии из закона Амдала: для того чтобы ускорить выполнение программы в q раз необходимо ускорить не менее, чем
в (1-1/ q )-ю часть программы. Следовательно, если есть желание ускорить программу в 100 раз по сравнению с ее последовательным вариантом, то необходимо получить ускорение не менее, чем на 99.99% кода, что почти всегда составляет значительную часть программы!
Отсюда первый вывод — прежде, чем основательно переделывать код для перехода на параллельный компьютер или суперкомпьютер надо основательно подумать. Если, оценив заложенный в программе алгоритм, ясно, что доля последовательных операций велика, то на значительное ускорение рассчитывать явно не приходится и нужно думать о замене отдельных компонент алгоритма.
В ряде случаев последовательный характер алгоритма изменить не так сложно. Допустим, что в программе есть следующий фрагмент для вычисления суммы n чисел: s = 0 Do i = 1, n s = s + a(i) EndDo По своей природе он строго последователен, так как на i-й итерации цикла требуется результат с (i-1)-й и все итерации выполняются одна за одной.
Имеем 100% последовательных операций, а значит и никакого эффекта от использования параллельных компьютеров. Вместе с тем, выход очевиден. Поскольку в большинстве реальных программ нет существенной разницы, в каком порядке складывать числа, выберем иную схему сложения. Сначала найдем сумму пар соседних элементов: a(1)+a(2), a(3)+a(4), a(5)+a(6) и т.д.
Заметим, что при такой схеме все пары можно складывать одновременно! На следующих шагах будем действовать абсолютно аналогично, получив вариант параллельного алгоритма. Казалось бы в данном случае все проблемы удалось разрешить. Но представьте, что доступные вам процессоры разнородны по своей производительности.
Значит будет такой момент, когда кто-то из них еще трудится, а кто-то уже все сделал и бесполезно простаивает в ожидании. Если разброс в производительности компьютеров большой, то и эффективность всей системы при равномерной загрузке процессоров будет крайне низкой. Но пойдем дальше и предположим, что все процессоры одинаковы. Проблемы кончились? Опять нет!
Процессоры выполнили свою работу, но результат-то надо передать другому для продолжения процесса суммирования, а на передачу уходит время и в это время процессоры опять простаивают. Словом, заставить параллельную вычислительную систему или суперЭВМ работать с максимальной эффективность на конкретной программе это,
задача не из простых, поскольку необходимо тщательное согласование структуры программ и алгоритмов с особенностями архитектуры параллельных вычислительных систем . Замечание: Верно ли утверждение: чем мощнее компьютер, тем быстрее на нем можно решить данную задачу? Нет, это не верно. Можно пояснить простым бытовым примером.
Если один землекоп выкопает яму 1м*1м*1м за 1 час, то два таких же землекопа это сделают за 30 мин — в это можно поверить. А за сколько времени эту работу сделают 60 землекопов? За 1 минуту? Конечно же нет! Начиная с некоторого момента они будут просто мешаться друг другу, не ускоряя, а замедляя процесс.
Так же и в компьютерах: если задача слишком мала, то мы будем дольше заниматься распределением работы, синхронизацией процессов, сборкой результатов и т.п., чем непосредственно полезной работой.
Источник: studfile.net
Ускорения параллельных вычислений
Главной целью создания и разработки многочисленных типов параллельных машин, о которых мы говорили в прошлой статье, это скорость. Суперкомпьютеры и многопроцессорные системы могут и должны делать все быстрее! Давайте постараемся расчитать, насколько быстрее.
Логично подумать, что если один процессор выполняет работу за n секунд, то четыре процессора потратят n/4 секунд. Понятие “фактор ускорения” (“speedup factor”) это отношение времени, которое тратит на выполнение работы один процессор к времени, которое тратит на эту же работу многопроцессорная система.
Для расчета важно использовать самый оптимальный Ts, то есть лучший из возможных не-параллельных алгоритмов.
Теперь плохие новости: у этого ускорения есть лимит. Называется он Amdahl’s Law (Закон Амдала) и вот его суть: так выглядит какая-либо задача на обычной однопроцессорной системе:

Все время выполнения — знакомое уже нам Ts, состоит из той части, которую можно распределить на несколько процессоров (распараллелить) — (1-f)Ts, и той части, что распараллелить нельзя (серийная) — fTs.
Как будет выглядеть схема той же задачи для нескольких процессоров?

Теперь общее время выполнения Tp состоит из серийного времени и максимального из тех, что мы распределили на несколько процессоров (выполняются они все одновременно, но ждать нужно самого медленного). Для простоты допустим, что все они занимают одинаковое время.
Фактор ускорения расчитывается по формуле:

То есть все зависит от того, какой кусок программы мы сможем распараллелить (f в процентах означает количество серийного кода). Если f=0%, то есть абсолютно весь код распараллелен (чего практически не может быть), то чем больше процессоров мы задействуем, тем быстрее будет выполнена задача, и соотношение будет линейное: хотим в 10 раз быстрее — используем десять процессоров, хотим в миллион раз быстрее — закупаем миллион процессоров. Но вот стоит оставить 5% серийного кода, а 95% распараллелить, то фактор ускорения будет равен 20 и выше никак не прыгнуть. Даже если закупим к тому миллиону еще миллион процессоров, то программа все равно будет выполняться в 20 раз быстрее. Вот как этот грустный факт выглядит на графике с примерами разных процентов f:

Получается, что самое важное в вопросе эффективности параллельного кода — это хороший дизайн самого алгоритма. Каждая деталь может сильно повлиять на расширяемость: если сейчас алгоритм нормально использует ресурсы четырехядерного процессора, то возможно больше 8 ядер он нормально использовать не сможет, и тогда через год программу нужно будет писать заново — ведь вместо количества транзисторов теперь каждые полгода увеличивается количество ядер!
Чтобы написать хороший параллельный алгоритм, нужно вникнуть в суть проблемы и подумать, как его можно разделить на отдельные независимые (в идеале) части, чтобы все они выполнялись параллельно на разных процессорах. Посмотрим на примере довольно ёмкой задачи умножения матрицы А на вектор b. Результат будет записан в вектор y, который по размеру идентичен вектору b. Чтобы получить первое значение вектора y, нужно умножить первую строку матрицы на вектор b, чтобы получить второе значение y — вторую строку на b, и так далее. Получается, каждый элемент вектора y можно считать независимо от других, то есть параллельно.

Размер каждой такой задачи один и тот же — все строки A имеют одинаковый размер (пока не касаемся таких деталей, как плотность матрицы — возможно, в ней много нулей, но предположим, что это не сильно влияет на время выполнения). Нет никаких зависимостей между задачами, и все задачи используют один и тот же b.
Вот другой пример — запрос в базу данных:
MODEL = “CIVIC” AND YEAR=2001 AND (COLOR=”GREEN” OR COLOR=”WHITE”);
Запрос пытается получить все зеленые или белые Цивики 2001 года из такой базы:

Такую задачу можно разложить на три части: один процессор будет формировать таблицу все Цивиков 2001 года, другой процессор будет формировать таблицу всех белых и зеленых машин (эти два запроса могут идти параллельно), после чего результат join’а этих двух таблиц и будет ответом.

Можно изменить структуру запроса, что может повлиять на параллелизацию

Разделение задачи на части для последующего распределения этих частей на разные процессоры называется декомпозицией. Умножение матрицы на вектор это пример декомпозиции результата задачи: результат (вектор y) был разделен на несколько независимых частей и каждая расчитывалась отдельно от другой. То же самое можно сделать и с перемножением матриц:

Наша первая параллельная программа
Для написания нашей первой параллельной программы мы будем использовать Cilk. Это язык программирования, который по сути является С с удобными инструментами для параллелизации и синхронизации задач.
Cilk был разработан в MIT в 1994 году, был бесплатным и свободным, но к 2006 году стал коммерциализироваться, стал поддерживать С++, а год назад был куплен с потрохами компанией Intel, которой, конечно же, выгодно иметь хороший язык программирования для многоядерных систем: они ведь саим такие системы и производят. Я не уверен, как можно получить компилятор бесплатно, в нашем университете есть академическая версия для студентов (разработчик Cilk хороший друг профессора), поэтому прошу меня извинить, если вы не сможете найти его. Но поискать, я считаю, стоит, потому что Cilk жутко прост и удобен! Не сравнить с Pthreads. Все, что нам нужно знать, чтобы начать программировать, это три ключевых слова: cilk, spawn и sync.
Лучше всего начать с примера, поэтому вот вам любимая всеми рекурсивная задача — числа Фибоначи — на Си:
int fib (int n) < if (n<2) return n; else < int x, y; x = fib (n-1); y = fib (n-2); return (x+y); >>
А вот та же программа на Cilk:
cilk int fib (int n) < if (n<2) return n; else < int x, y; x = spawn fib (n-1); y = spawn fib (n-2); sync; return (x+y); >>
Ключевое слово cilk используется для указания функции. Самыми главными являются слова spawn и sync. Spawn ставится перед вызовом функции, которую мы хотим запустить на другом ядре, а sync ждет окончания выполнения всех вызванных ранее spawn’ами функций. То есть строчка
x=spawn fib(n-1);
запускается на другом ядре, и сразу выполняется строчка y=spawn fib(n-2). Перед тем, как вернуть результат (return (x+y)) нужно дождаться окончания выполнения, иначе в переменных x и y не будет правильных значений. Это делает команда sync — как и понятно из названия.
Такая программа хоршенько загрузит множество ядер! Вот как выглядит схема работы этого алгоритма для n=4:

Цвета подсветки кода соответствуют цветам узлов графа. Каждый уровень графа выполняется одновременно, то есть первый вызов для n=4 вызывает две функции — для 3 и 2, они в свою очередь — для 2 и 1 и для 1 и 0 соответственно.

Вот исходный код этой программы:
В следующей статье мы поговорим о том, как расчитывается масштабируемость параллельных алгоритмов, какие виды шедулинга бывают и какой используется в cilk, а также коснемся сортировки и параллельного динамического программирования.
- параллельные вычисления
- cilk
Источник: habr.com