В данном разделе размещены примеры с подробным решением задач по темам:
- Графическое решение задач линейного программирования (7 задач)
- Симплекс-метод решения задач линейного программирования (8 задач)
- Двойственные задачи линейного программирования (3 задачи)
- Задачи линейного программирования в Excel (8 задач)
- Транспортная задача (8 задач)
- Транспортные задачи в Excel (5 задач)
- Задача о назначениях (3 задачи)
- Целочисленные задачи линейного программирования (5 задач)
- Дробно-линейное программирование (1 задача)
- Задачи нелинейного программирования (10 задач)
- Многокритериальная оптимизация (5 задач)
Может быть интересно:
- Решенные контрольные по ЛП
- Примеры по теории игр
- Примеры решений по ЭММ
- Динамическое программирование: примеры решений
Консультируем по задачам по линейного программирования
Python. Линейный алгоритм
- Отправить заявку
- Услуги и предметы
- Онлайн-помощь
- Сдача тестов
- Отзывы клиентов
- Цены и оплата
- О заказе и гарантиях
- Оформление работ
- Вопросы и ответы
- Примеры решений задач
- Онлайн решение задач
- Программы-решатели
- Учебники и видеоуроки
- Статьи о математике
- Полезные сайты
- Формулы и справочники
- Онлайн учебник
- Примеры решений
- Онлайн калькуляторы
- Формулы и таблицы
- Статьи по ТВ
- Учебники и ссылки
МатБюро поможет
Вы также можете:
Оптимальный выбор
МатБюро помогает студентам с 2006 года. Всё это время мы поддерживаем прекрасную репутацию и наилучшие условия «цена-качество».
Мы предлагаем:
Грамотную и подробную консультацию и решение за разумную стоимость.
- Количество Более 96000
выполненных
заказов - Цены Разумные и
обоснованные
цены - Опыт Помогаем студентам
в решении задач
уже 16 лет - Кредо Качество,
ответственность
и уважение - И еще Мы рады
выполнить
ваш заказ
Источник: www.matburo.ru
Лекция 3: Математическое программирование. Линейное программирование. Виды задач линейного программирования. Постановка задач линейного программирования и исследование их структуры. Решение задач линейного программирования симплекс-методом
Аннотация: Данная лекция раскрывает ряд вопросов, посвященных линейному программированию как одному из разделов математического программирования; в частности, формулирует основные виды задач линейного программирования, раскрывает отличия данных задач от классических задач математического анализа; знакомит с различными формами записи данных задач, осуществляет их постановку и исследование структуры. Наиболее полно раскрыт вопрос о решении задач линейного программирования симплекс-методом.
Линейные программы. Решение задач. Ч.1.
1. Понятие математического программирования
Математическое программирование – это математическая дисциплина, в которой разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями.
Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах математического программирования оказываются непригодными.
Для решения задач математического программирования разработаны и разрабатываются специальные методы и теории. Так как при решении этих задач приходится выполнять значительный объем вычислений, то при сравнительной оценке методов большое значение придается эффективности и удобству их реализации на ЭВМ.
Математическое программирование можно рассматривать как совокупность самостоятельных разделов, занимающихся изучением и разработкой методов решения определенных классов задач.
В зависимости от свойств целевой функции и функции ограничений все задачи математического программирования делятся на два основных класса:
- задачи линейного программирования,
- задачи нелинейного программирования .
Если целевая функция и функции ограничений – линейные функции, то соответствующая задача поиска экстремума является задачей линейного программирования. Если хотя бы одна из указанных функций нелинейна, то соответствующая задача поиска экстремума является задачей нелинейного программирования .
2. Понятие линейного программирования. Виды задач линейного программирования
Линейное программирование (ЛП) – один из первых и наиболее подробно изученных разделов математического программирования . Именно линейное программирование явилось тем разделом, с которого и начала развиваться сама дисциплина » математическое программирование «. Термин «программирование» в названии дисциплины ничего общего с термином «программирование (т.е. составление программы) для ЭВМ» не имеет, т.к. дисциплина » линейное программирование » возникла еще до того времени, когда ЭВМ стали широко применяться для решения математических, инженерных, экономических и др. задач.
Итак, линейное программирование возникло после второй мировой войны и стало быстро развиваться, привлекая внимание математиков, экономистов и инженеров благодаря возможности широкого практического применения, а также математической стройности.
Можно сказать, что линейное программирование применимо для решения математических моделей тех процессов и систем, в основу которых может быть положена гипотеза линейного представления реального мира.
Линейное программирование применяется при решении экономических задач, в таких задачах как управление и планирование производства; в задачах определения оптимального размещения оборудования на морских судах, в цехах; в задачах определения оптимального плана перевозок груза (транспортная задача); в задачах оптимального распределения кадров и т.д.
Задача линейного программирования (ЛП), как уже ясно из сказанного выше, состоит в нахождении минимума (или максимума) линейной функции при линейных ограничениях.

Общая форма задачи имеет вид: найти при условиях
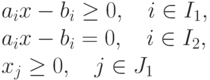
Здесь и далее нам удобнее считать с и аі вектор — строками, а x и b=(b1. bm) T — вектор столбцами.
Наряду с общей формой широко используются также каноническая и стандартная формы. Как в канонической, так и в стандартной форме
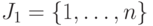
т.е. все переменные в любом допустимом решении задачи должны принимать неотрицательные значения (такие переменные принято называть неотрицательные в отличие от так называемых свободных переменных, на область значений которых подобное ограничение не накладывается). Отличие же между этими формами состоит в том, что в одном случае I2 = 0 , а в другом — I1 = 0 .
Задача ЛП в канонической форме:
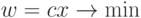 |
( 2.1) |
 |
( 2.2) |
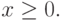 |
( 2.3) |
Задача ЛП в стандартной форме:
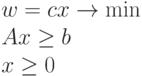
Источник: intuit.ru
Как решать линейные уравнения

АЛГЕБРА
Автор Ольга Викторовна Опубликовано 22.08.2019
Уравнение представляет собой математическое утверждение , что два выражения равны, например, . Решением уравнения является любой набор значений, который может заменить переменные для создания истинного оператора. Рассмотрим какие уравнения являются линейными, как решать линейные уравнения, какие правила для решения линейных уравнений надо знать и применять.
Линейное уравнение и его решение
Линейным называется уравнение, в котором x – переменная входит в первой степени. Почему линейное уравнение называется линейным? Потому что им описывается прямая (линия). Решать такое уравнение легко и просто – вам нужно просто разделить по разным сторонам от знака = неизвестные и известные в уравнении. А далее применить необходимые преобразования, если они нужны, или сразу же найти корень уравнения.
Простое решение
Переменная в уравнении это и решение будет . Чтобы убедиться в этом, замените значение в уравнении и получите истинное утверждение:
Особенно полезны уравнения, связывающие две переменные. Если мы знаем значение одной из переменных, мы можем найти соответствующее значение другой переменной, решая уравнение.
Пример: Уравнение определяет заработную плату Эмили , где – количество часов, которые необходимо работать в неделю. Сколько часов нужно будет работать Эмили на следующей неделе, если она хочет заработать 3600 рублей?
Решение: Понятно, что в этом случае , подставляем это значение в уравнение и находим :
Итак, получается, что Эмили нужно проработать 60 часов.
Чтобы решить уравнение, мы можем получить более простые уравнения, которые имеют одинаковые решения.

Уравнения, имеющие одинаковые решения, называются эквивалентными уравнениями. Например,
имеют одинаковые решения, то есть являются эквивалентными. Это, конечно, написано математически строгим языком, но сложно для понимания школьника.
Объясню проще: пусть нам дано уравнение . Итак, отделим известные от неизвестных. Обычно, неизвестные отправляют в левую часть от знака “=”, а известные – отправляют в правую часть, при этом мы при переносе всегда меняем знак на противоположный:
. Это – эквивалентное линейное уравнение самому первому уравнению.
Теперь находим неизвестный множитель:
Итак, корень уравнения .
Желательно, если вы только начинаете решать линейные уравнения, сначала всегда проводите проверку – подставим полученный корень в исходное (самое первое) уравнение:
![]()
. Мы получили верное равенство, значит, уравнение решено верно.
Еще примеры решения линейных уравнений
1.Решите уравнение В данном уравнении x-неизвестный множитель. Вспомним правило:
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Правила записи: чтобы писать математически грамотно решение линейного уравнение – каждое вычисление или преобразование надо делать с новой строки. Недопустимым считается следующее написание: . По правилам математической грамотности, на одной строчке мы пишем , и только на следующей . Будьте грамотны.
2. Решите уравнение . В данном уравнении x – неизвестное слагаемое. Правило:
Для того, чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое.
3. Решите уравнение . В данном уравнении x- неизвестное вычитаемое. Правило:
Чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность.
Решение: уменьшаемое у нас 3, а разность 9: .
4. Решите уравнение . В данном уравнении x- неизвестное уменьшаемое. Правило:
Для того, чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
5. Решите линейное уравнение . Здесь x – неизвестное делимое. Правило:
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
6. Решите уравнение . Здесь x-неизвестный делитель. Правило:
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Это самые простые линейные уравнения. Что же делать если у нас уравнение линейное, но сложное, уровень которого не 3-4 класс, а 7-9? Как решить его?
Универсальный метод
Универсальный метод того, как решать линейные уравнения, заключается в сведении сложного уравнения к простому, правила для которого известны. Понятнее будет на примере:
Вроде есть все – и сложение, и вычитание и деление и умножение. Какое правило применять? Непонятно. Давайте упростим это уравнение. Начнем с его левой части: , тогда в левой части будет:
Теперь приведем две дроби и к общему знаменателю:
. Запишем под одним знаменателем:
. Умножим левую и правую части уравнения на 2. По правилам мы можем умножать левую и правую части уравнения (как и делить) на одно и то же число, отличное от нуля, и это не повлияет на его ответ. Тогда, знаменатель в левой части сократится, и мы получим:
А теперь мы просто находим неизвестный множитель:
![]() .
.
![]()
Метод понятен – постепенными преобразованиями мы привели исходное уравнение к простому, эквивалентному исходному. А затем, просто применили известные правила из начальной школы. Теперь вы знаете, как решать линейные уравнения простые и сложные. Это поможет вам в подготовке к ЕГЭ по математике.
Источник: repetitor-mathematics.ru