Как реализовать графы в программе

Что такое граф, классификация графов, реализация на C++

Граф – совокупность точек, соединенных линиями. Точки называются вершинами , или узлами , а линии – ребрами , или дугами .

Степень входа вершины – количество входящих в нее ребер, степень выхода – количество исходящих ребер.

Граф, содержащий ребра между всеми парами вершин, является полным .

Встречаются такие графы, ребрам которых поставлено в соответствие конкретное числовое значение, они называются взвешенными графами , а это значение – весом ребра .

Когда у ребра оба конца совпадают, т.е. оно выходит из вершины и входит в нее, то такое ребро называется петлей .

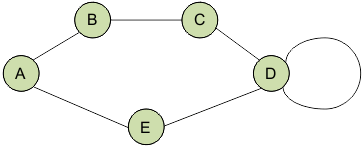
Классификация графов

Графы делятся на

В связном графе между любой парой вершин существует как минимум один путь.

В несвязном графе существует хотя бы одна вершина, не связанная с другими.

BP2-3-1-07 Простейшая реализация графа

Графы также подразделяются на

• ориентированные

• неориентированные

• смешанные

В ориентированном графе ребра являются направленными, т.е. существует только одно доступное направление между двумя связными вершинами.

В неориентированном графе по каждому из ребер можно осуществлять переход в обоих направлениях.

Частный случай двух этих видов – смешанный граф. Он характерен наличием как ориентированных, так и неориентированных ребер.

Способы представления графа

Граф может быть представлен (сохранен) несколькими способами:

• матрица смежности;
• матрица инцидентности;
• список смежности (инцидентности);
• список ребер.

Использование двух первых методов предполагает хранение графа в виде двумерного массива (матрицы). Размер массива зависит от количества вершин и/или ребер в конкретном графе.

Матрица смежности графа — это квадратная матрица, в которой каждый элемент принимает одно из двух значений: 0 или 1.

Число строк матрицы смежности равно числу столбцов и соответствует количеству вершин графа.

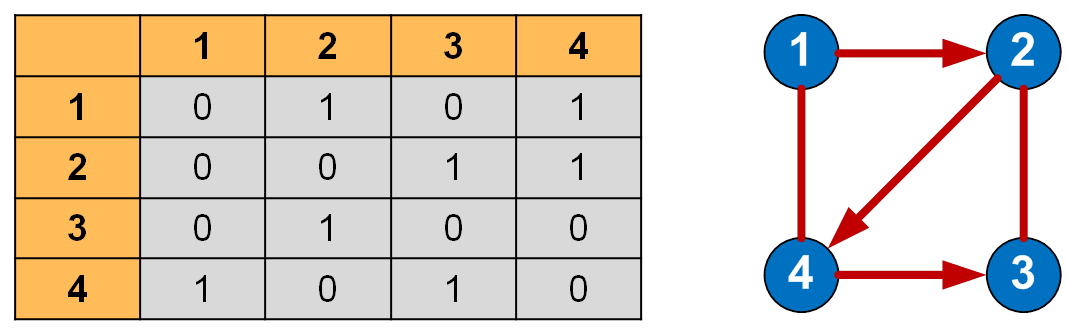
• 0 – соответствует отсутствию ребра,
• 1 – соответствует наличию ребра.

Когда из одной вершины в другую проход свободен (имеется ребро), в ячейку заносится 1, иначе – 0. Все элементы на главной диагонали равны 0 если граф не имеет петель.

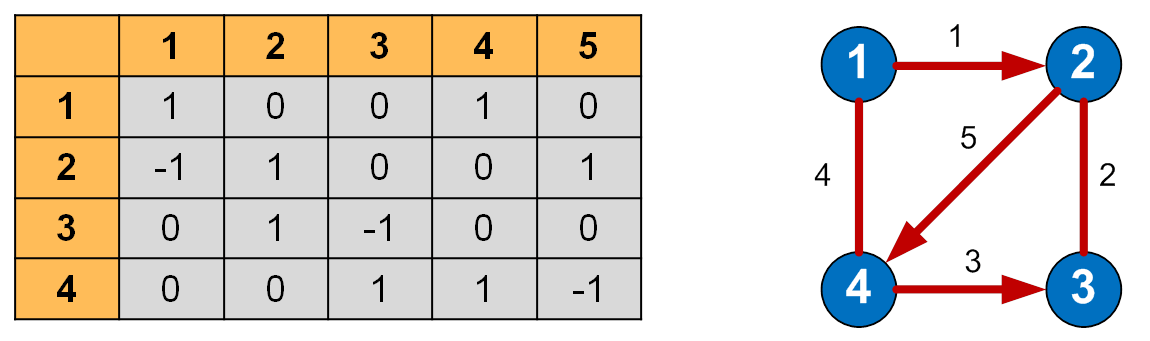
Матрица инцидентности (инциденции) графа — это матрица, количество строк в которой соответствует числу вершин, а количество столбцов – числу рёбер. В ней указываются связи между инцидентными элементами графа (ребро(дуга) и вершина).

В неориентированном графе если вершина инцидентна ребру то соответствующий элемент равен 1, в противном случае элемент равен 0.

#3. Алгоритм Дейкстры (Dijkstra’s algorithm) | Алгоритмы на Python

В ориентированном графе если ребро выходит из вершины, то соответствующий элемент равен 1, если ребро входит в вершину, то соответствующий элемент равен -1, если ребро отсутствует, то элемент равен 0.

Матрица инцидентности для своего представления требует нумерации рёбер, что не всегда удобно.

Список смежности (инцидентности)
Если количество ребер графа по сравнению с количеством вершин невелико, то значения большинства элементов матрицы смежности будут равны 0. При этом использование данного метода нецелесообразно. Для подобных графов имеются более оптимальные способы их представления.

По отношению к памяти списки смежности менее требовательны, чем матрицы смежности. Такой список можно представить в виде таблицы, столбцов в которой – 2, а строк — не больше, чем вершин в графе.
В каждой строке в первом столбце указана вершина выхода, а во втором столбце – список вершин, в которые входят ребра из текущей вершины.

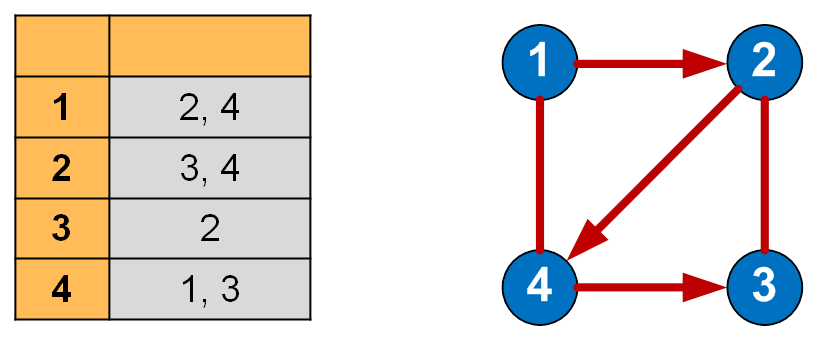
Преимущества списка смежности:

• Рациональное использование памяти.
• Позволяет быстро перебирать соседей вершины.
• Позволяет проверять наличие ребра и удалять его.

Недостатки списка смежности:

• При работе с насыщенными графами (с большим количеством рёбер) скорости может не хватать.
• Нет быстрого способа проверить, существует ли ребро между двумя вершинами.
• Количество вершин графа должно быть известно заранее.
• Для взвешенных графов приходится хранить список, элементы которого должны содержать два значащих поля, что усложняет код:

• номер вершины, с которой соединяется текущая;
• вес ребра.

Список рёбер
В списке рёбер в каждой строке записываются две смежные вершины и вес соединяющего их ребра (для взвешенного графа).
Количество строк в списке ребер всегда должно быть равно величине, получающейся в результате сложения ориентированных рёбер с удвоенным количеством неориентированных рёбер.

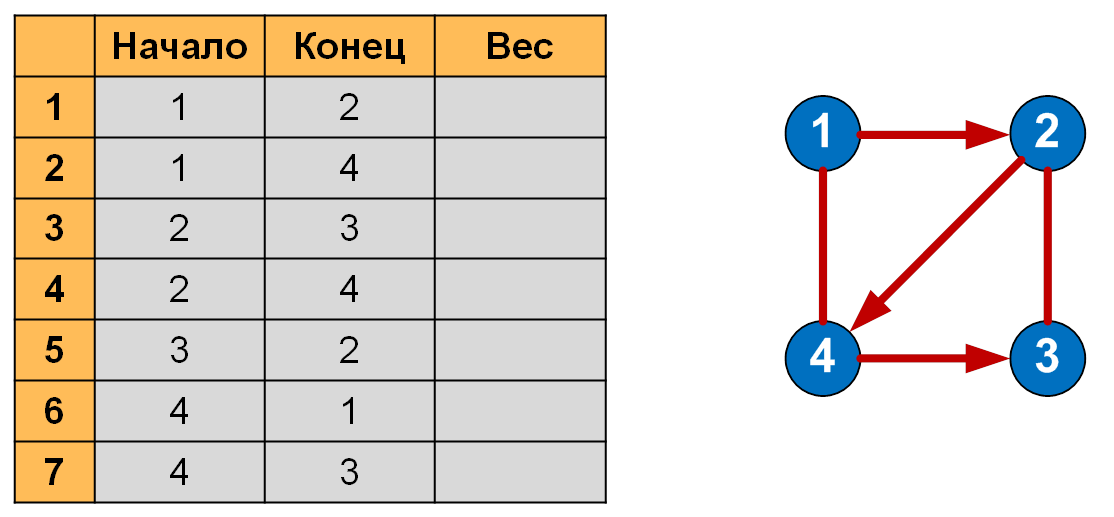
Какой способ представления графа лучше? Ответ зависит от отношения между числом вершин и числом рёбер. Число ребер может быть довольно малым (такого же порядка, как и количество вершин) или довольно большим (если граф является полным). Графы с большим числом рёбер называют плотными , с малым — разреженными . Плотные графы удобнее хранить в виде матрицы смежности, разреженные — в виде списка смежности.

Алгоритмы обхода графов

Основными алгоритмами обхода графов являются

• Поиск в ширину
• Поиск в глубину

Поиск в ширину подразумевает поуровневое исследование графа:

• вначале посещается корень – произвольно выбранный узел,
• затем – все потомки данного узла,
• после этого посещаются потомки потомков и т.д.

Вершины просматриваются в порядке возрастания их расстояния от корня.
Алгоритм прекращает свою работу после обхода всех вершин графа, либо в случае выполнения требуемого условия (например, найти кратчайший путь из вершины 1 в вершину 6).
Каждая вершина может находиться в одном из 3 состояний:

• 0 — оранжевый – необнаруженная вершина;
• 1 — зеленый – обнаруженная, но не посещенная вершина;
• 2 — серый – обработанная вершина.

Фиолетовый – рассматриваемая вершина.

Применения алгоритма поиска в ширину

• Поиск кратчайшего пути в невзвешенном графе (ориентированном или неориентированном).
• Поиск компонент связности.
• Нахождения решения какой-либо задачи (игры) с наименьшим числом ходов.
• Найти все рёбра, лежащие на каком-либо кратчайшем пути между заданной парой вершин.
• Найти все вершины, лежащие на каком-либо кратчайшем пути между заданной парой вершин.

Алгоритм поиска в ширину работает как на ориентированных, так и на неориентированных графах.
Для реализации алгоритма удобно использовать очередь.

Реализация на C++ (с использованием очереди STL)

#include #include // очередь using namespace std; int main() < queueQueue; int mas[7][7] = < < 0, 1, 1, 0, 0, 0, 1 >, // матрица смежности < 1, 0, 1, 1, 0, 0, 0 >, < 1, 1, 0, 0, 0, 0, 0 >, < 0, 1, 0, 0, 1, 0, 0 >, < 0, 0, 0, 1, 0, 1, 0 >, < 0, 0, 0, 0, 1, 0, 1 >, < 1, 0, 0, 0, 0, 1, 0 >>; int nodes[7]; // вершины графа for (int i = 0; i < 7; i++) nodes[i] = 0; // исходно все вершины равны 0 Queue.push(0); // помещаем в очередь первую вершину while (!Queue.empty()) < // пока очередь не пуста int node = Queue.front(); // извлекаем вершину Queue.pop(); nodes[node] = 2; // отмечаем ее как посещенную for (int j = 0; j < 7; j++) < // проверяем для нее все смежные вершины if (mas[node][j] == 1 nodes[j] == 0) < // если вершина смежная и не обнаружена Queue.push(j); // добавляем ее в очередь nodes[j] = 1; // отмечаем вершину как обнаруженную >> cout cin.get(); return 0; >

Результат выполнения

1 2 3 7 4 6 5

Задача поиска кратчайшего пути
Реализация на С++

#include #include // очередь #include // стек using namespace std; struct Edge < int begin; int end; >; int main() < system(«chcp 1251»); system(«cls»); queueQueue; stack Edges; int req; Edge e; int mas[7][7] = < < 0, 1, 1, 0, 0, 0, 1 >, < 1, 0, 1, 1, 0, 0, 0 >, < 1, 1, 0, 0, 0, 0, 0 >, < 0, 1, 0, 0, 1, 0, 0 >, < 0, 0, 0, 1, 0, 1, 0 >, < 0, 0, 0, 0, 1, 0, 1 >, < 1, 0, 0, 0, 0, 1, 0 >>; int nodes[7]; // вершины графа for (int i = 0; i < 7; i++) // исходно все вершины равны 0 nodes[i] = 0; cout > req; req—; Queue.push(0); // помещаем в очередь первую вершину while (!Queue.empty()) < int node = Queue.front(); // извлекаем вершину Queue.pop(); nodes[node] = 2; // отмечаем ее как посещенную for (int j = 0; j < 7; j++) < if (mas[node][j] == 1 nodes[j] == 0) < // если вершина смежная и не обнаружена Queue.push(j); // добавляем ее в очередь nodes[j] = 1; // отмечаем вершину как обнаруженную e.begin = node; e.end = j; Edges.push(e); if (node == req) break; >> cout cout > cin.get(); cin.get(); return 0; >

Результат выполнения

N = 6 1 2 3 7 4 6 5 Путь до вершины 6 6
N = 4 1 2 3 7 4 6 5 Путь до вершины 4 4

Поиск в глубину – это алгоритм обхода вершин графа.

Поиск в ширину производится симметрично (вершины графа просматривались по уровням). Поиск в глубину предполагает продвижение вглубь до тех пор, пока это возможно. Невозможность продвижения означает, что следующим шагом будет переход на последний, имеющий несколько вариантов движения (один из которых исследован полностью), ранее посещенный узел (вершина).

Отсутствие последнего свидетельствует об одной из двух возможных ситуаций:

• все вершины графа уже просмотрены,
• просмотрены вершины доступные из вершины, взятой в качестве начальной, но не все (несвязные и ориентированные графы допускают последний вариант).

Каждая вершина может находиться в одном из 3 состояний:

• 0 — оранжевый – необнаруженная вершина;
• 1 — зеленый – обнаруженная, но не посещенная вершина;
• 2 — серый – обработанная вершина;

Фиолетовый – рассматриваемая вершина.

Применения алгоритма поиска в глубину

• Поиск любого пути в графе.
• Поиск лексикографически первого пути в графе.
• Проверка, является ли одна вершина дерева предком другой.
• Поиск наименьшего общего предка.
• Топологическая сортировка.
• Поиск компонент связности.

Алгоритм поиска в глубину работает как на ориентированных, так и на неориентированных графах. Применимость алгоритма зависит от конкретной задачи.
Для реализации алгоритма удобно использовать стек или рекурсию.

Реализация на C++ (с использованием стека STL)

#include #include // стек using namespace std; int main() < stackStack; int mas[7][7] = < < 0, 1, 1, 0, 0, 0, 1 >, // матрица смежности < 1, 0, 1, 1, 0, 0, 0 >, < 1, 1, 0, 0, 0, 0, 0 >, < 0, 1, 0, 0, 1, 0, 0 >, < 0, 0, 0, 1, 0, 1, 0 >, < 0, 0, 0, 0, 1, 0, 1 >, < 1, 0, 0, 0, 0, 1, 0 >>; int nodes[7]; // вершины графа for (int i = 0; i < 7; i++) // исходно все вершины равны 0 nodes[i] = 0; Stack.push(0); // помещаем в очередь первую вершину while (!Stack.empty()) < // пока стек не пуст int node = Stack.top(); // извлекаем вершину Stack.pop(); if (nodes[node] == 2) continue; nodes[node] = 2; // отмечаем ее как посещенную for (int j = 6; j >= 0; j—) < // проверяем для нее все смежные вершины if (mas[node][j] == 1 nodes[j] != 2) < // если вершина смежная и не обнаружена Stack.push(j); // добавляем ее в cтек nodes[j] = 1; // отмечаем вершину как обнаруженную >> cout cin.get(); return 0; >

Результат выполнения

1 2 3 4 5 6 7

Задача поиска лексикографически первого пути на графе.
Реализация на C++

#include //#include // очередь #include // стек using namespace std; struct Edge < int begin; int end; >; int main() < system(«chcp 1251»); system(«cls»); stackStack; stack Edges; int req; Edge e; int mas[7][7] = < < 0, 1, 1, 0, 0, 0, 1 >, // матрица смежности < 1, 0, 1, 1, 0, 0, 0 >, < 1, 1, 0, 0, 0, 0, 0 >, < 0, 1, 0, 0, 1, 0, 0 >, < 0, 0, 0, 1, 0, 1, 0 >, < 0, 0, 0, 0, 1, 0, 1 >, < 1, 0, 0, 0, 0, 1, 0 >>; int nodes[7]; // вершины графа for (int i = 0; i < 7; i++) // исходно все вершины равны 0 nodes[i] = 0; cout > req; req—; Stack.push(0); // помещаем в очередь первую вершину while (!Stack.empty()) < // пока стек не пуст int node = Stack.top(); // извлекаем вершину Stack.pop(); if (nodes[node] == 2) continue; nodes[node] = 2; // отмечаем ее как посещенную for (int j = 6; j >= 0; j—) < // проверяем для нее все смежные вершины if (mas[node][j] == 1 nodes[j] != 2) < // если вершина смежная и не обнаружена Stack.push(j); // добавляем ее в cтек nodes[j] = 1; // отмечаем вершину как обнаруженную e.begin = node; e.end = j; Edges.push(e); if (node == req) break; >> cout cout > cin.get(); cin.get(); return 0; >
N = 6 1 2 3 4 5 6 7 Путь до вершины 6 6
N = 4 1 2 3 4 5 6 7 Путь до вершины 4 4

Поиск в глубину также может быть реализован с использованием рекурсивного алгоритма.

Реализация обхода графа в глубину на C++ (с использованием рекурсии)

#include using namespace std; int mas[7][7] = < < 0, 1, 1, 0, 0, 0, 1 >, // матрица смежности < 1, 0, 1, 1, 0, 0, 0 >, < 1, 1, 0, 0, 0, 0, 0 >, < 0, 1, 0, 0, 1, 0, 0 >, < 0, 0, 0, 1, 0, 1, 0 >, < 0, 0, 0, 0, 1, 0, 1 >, < 1, 0, 0, 0, 0, 1, 0 >>; int nodes[7]; // вершины графа void search(int st, int n) < int r; cout int main() < for (int i = 0; i < 7; i++) // исходно все вершины равны 0 nodes[i] = 0; search(0, 7); cin.get(); return 0; >

Результат выполнения

Источник: bookflow.ru

Как реализовать графы в программе

2. Поиск в глубину (Depth First Searching)

Поиск в глубину или обход в глубину — это рекурсивный алгоритм поиска всех вершин графа или древовидной структуры данных.

Алгоритм поиска в глубину (DFS) осуществляет поиск вглубь графа, а также использует стек, чтобы не забыть «получить» следующую вершину для начала поиска, когда на любой итерации возникает тупик.

Простой алгоритм, который нужно запомнить, для DFS:

1. Посетите соседнюю непосещенную вершину. Отметьте как посещенную. Отобразите это. Добавьте в стек.
2. Если смежная вершина не найдена, то вершина берется из стека. Стек выведет все вершины, у которых нет смежных вершин.
3. Повторяйте шаги 1 и 2, пока стек не станет пустым.

Схематическое представление обхода DFS:

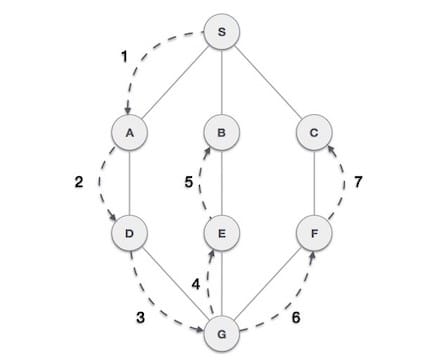
Если хочешь подтянуть свои знания по алгоритмам, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:

• углубишься в теорию структур данных;
• научишься решать сложные алгоритмические задачи;
• научишься применять алгоритмы и структуры данных при разработке программ.

3. Топологическая сортировка (Topological Sorting)

Топологическая сортировка для ориентированного ациклического графа (DAG) — это линейное упорядочивание вершин, при котором вершина u предшествует v для каждого направленного ребра uv (в порядке очереди). Топологическая сортировка для графа невозможна, если граф не является DAG.

Для одного графа может применяться более одной топологической сортировки.

Простой алгоритм, который следует запомнить, для топологической сортировки:

1. Отметьте u как посещенную

2. Для всех вершин v , смежных с u , выполните:

2.1. Если v не посещенная, то:

2.2. Выполняем TopoSort (не забывая про стек)

2.3. Цикл выполнен

3. Запишите u в стек

Схематическое представление топологической сортировки:

Пример топологической сортировки для этого графа:

5 → 4 → 2 → 3 → 1 → 0

4. Обнаружение цикла с помощью алгоритма Кана (Kahn’s Algorithm)

Алгоритм топологической сортировки Кана — это алгоритм обнаружения циклов на базе эффективной топологической сортировки.

Работа алгоритма осуществляется путем нахождения вершины без входящих в нее ребер и удаления всех исходящих ребер из этой вершины.

5. Алгоритм Дейкстры (Dijkstra’s Algorithm)

Алгоритм Дейкстры позволяет найти кратчайший путь между любыми двумя вершинами графа. Он отличается от минимального остовного дерева тем, что кратчайшее расстояние между двумя вершинами может не включать все вершины графа.

Ниже проиллюстрирован алгоритм кратчайшего пути с одним источником. Здесь наличие одного источника означает, что мы должны найти кратчайший путь от источника ко всем узлам.

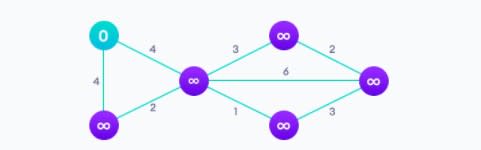
После применения алгоритма Дейкстры:

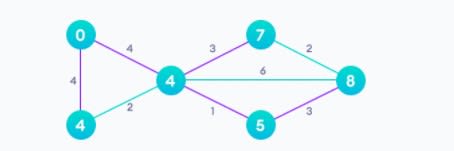
6. Алгоритм Беллмана-Форда (Bellman Ford’s Algorithm)

Алгоритм Беллмана-Форда помогает нам найти кратчайший путь от вершины ко всем другим вершинам взвешенного графа. Он похож на алгоритм Дейкстры, но может обнаруживать графы, в которых ребра могут иметь циклы с отрицательным весом.

Алгоритм Дейкстры (не обнаруживает цикл с отрицательным весом) может дать неверный результат, потому что проход через цикл с отрицательным весом приведет к уменьшению длины пути. Дейкстра не применим для графиков с отрицательными весами, а Беллман-Форд, наоборот, применим для таких графиков. Беллман-Форд также проще, чем Дейкстра и хорошо подходит для систем с распределенными параметрами.

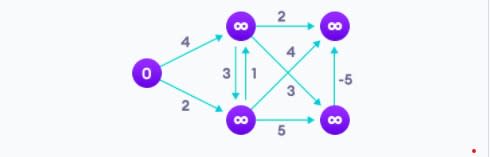
Результат алгоритма Беллмана-Форда:

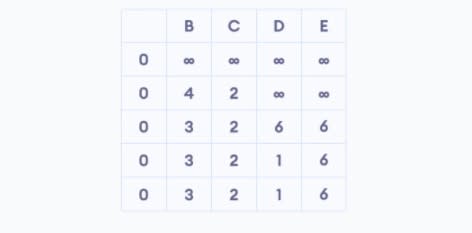
7. Алгоритм Флойда-Уоршалла (Floyd-Warshall Algorithm)

Алгоритм Флойда-Уоршалла — это алгоритм поиска кратчайшего пути между всеми парами вершин во взвешенном графе. Этот алгоритм работает как для ориентированных, так и для неориентированных взвешенных графов. Но это не работает для графов с отрицательными циклами (где сумма ребер в цикле отрицательна). Здесь будет использоваться концепция динамического программирования.

Алгоритм, лежащий в основе алгоритма Флойда-Уоршалла:

8. Алгоритм Прима (Prim’s Algorithm)

Алгоритм Прима — это жадный алгоритм, который используется для поиска минимального остовного дерева из графа. Алгоритм Прима находит подмножество ребер, которое включает каждую вершину графа, так что сумма весов ребер может быть минимизирована.

Простой алгоритм для алгоритма Прима, который следует запомнить:

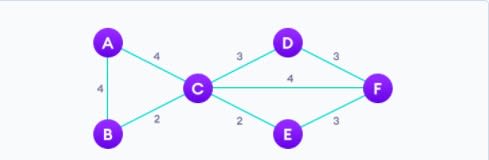
1. Выберите минимальное остовное дерево со случайно выбранной вершиной.
2. Найдите все ребра, соединяющие дерево с новыми вершинами, найдите минимум и добавьте его в дерево.
3. Продолжайте повторять шаг 2, пока мы не получим минимальное остовное дерево.

9. Алгоритм Краскала (Kruskal’s Algorithm)

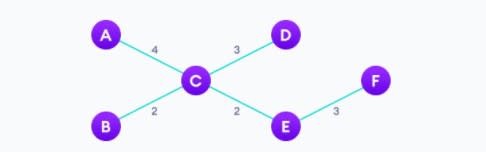
Алгоритм Краскала используется для нахождения минимального остовного дерева для связного взвешенного графа. Основная цель алгоритма — найти подмножество ребер, с помощью которых мы можем обойти каждую вершину графа. Он является жадным алгоритмом, т. к. находит оптимальное решение на каждом этапе вместо поиска глобального оптимума.

Простой алгоритм Краскала, который следует запомнить:

1. Сначала отсортируйте все ребра по весу (от наименьшего к наибольшему).
2. Теперь возьмите ребро с наименьшим весом и добавьте его в остовное дерево. Если добавляемое ребро создает цикл, не берите такое ребро.
3. Продолжайте добавлять ребра, пока не достигнете всех вершин и не будет создано минимальное остовное дерево.

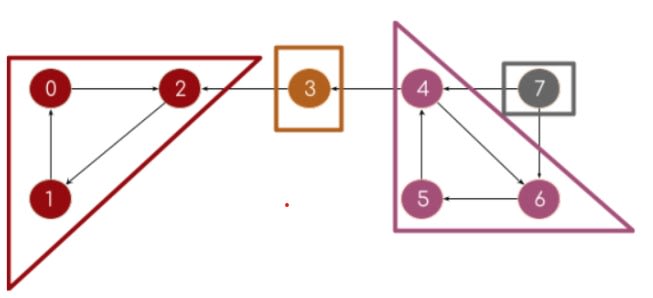
10. Алгоритм Косараджу (Kosaraju’s Algorithm)

Если мы можем достичь каждой вершины компонента из любой другой вершины этого компонента, то он называется сильно связанным компонентом (SCC). Одиночный узел всегда является SCC. Алгоритм Флойда-Уоршалла относится к методам полного перебора. Но для получения наилучшей временной сложности мы можем использовать алгоритм Косараджу.

Простой алгоритм Косараджу, который следует запомнить:

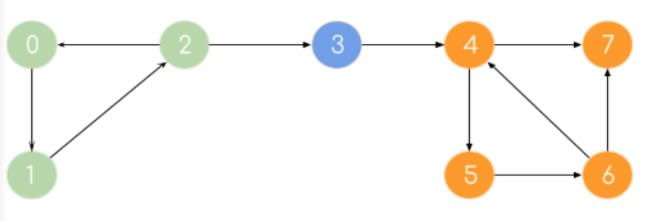
1. Выполните обход графа DFS. Поместите узел в стек перед возвратом.
2. Найдите граф транспонирования, поменяв местами ребра.
3. Извлекайте узлы один за другим из стека и снова в DFS на модифицированном графе.

В этой статье мы познакомились с самыми важными алгоритмами, которые должен знать каждый программист, работающий с графами. Если хотите подтянуть или освежить знания по алгоритмам и структурам данных, загляни на наш курс «Алгоритмы и структуры данных», который включает в себя:

• живые вебинары 2 раза в неделю;
• 47 видеолекций и 150 практических заданий;
• консультации с преподавателями курса.

Материалы по теме

• Деревья и графы: что это такое и почему их обязательно нужно знать каждому программисту
• ❓ Зачем разработчику знать алгоритмы и структуры данных?
• ❓ Пройди тест на знание алгоритмов и структур данных

Источники

Источник: proglib.io

Алгоритмы 101: как использовать алгоритмы на графах

Программирование и разработка

На чтение 17 мин Просмотров 984 Опубликовано 20.04.2021

Алгоритмы — одна из самых распространенных тем на собеседованиях по кодированию. Чтобы получить преимущество на собеседовании, важно хорошо знать основные алгоритмы и их реализации.

В сегодняшнем руководстве мы будем изучать алгоритмы графа. Мы начнем с введения в теорию графов и алгоритмы графов. Далее мы узнаем, как реализовать граф. Наконец, мы рассмотрим типичные проблемы с графами, которые вы можете ожидать увидеть на собеседовании по кодированию.

Что такое графовые алгоритмы?

Алгоритм — это математический процесс для решения проблемы с использованием четко определенного или оптимального количества шагов. Это просто базовая техника, используемая для выполнения конкретной работы.

Граф — это абстрактное обозначение, используемое для представления связи между всеми парами объектов. Графы — это широко используемые математические структуры, визуализируемые двумя основными компонентами: узлами и ребрами.

Алгоритмы графов используются для решения проблем представления графов в виде сетей, таких как рейсы авиакомпаний, подключение к Интернету или подключение к социальным сетям на Facebook. Они также популярны в НЛП и машинном обучении для формирования сетей.

Некоторые из лучших алгоритмов графа включают в себя:

• Реализовать обход в ширину
• Реализовать обход в глубину
• Вычислить количество узлов на уровне графа
• Найдите все пути между двумя узлами
• Найдите все компоненты связности графа
• Алгоритм Дейкстры для поиска кратчайшего пути в данных графа
• Удалить край

Хотя графики являются неотъемлемой частью дискретной математики, они также имеют практическое применение в информатике и программировании, включая следующее:

• Отношения вызывающий-вызываемый в компьютерной программе, представленной в виде графика
• Ссылочная структура веб-сайта может быть представлена ​​ориентированным графом.
• Нейронные сети реализованы с использованием

Свойства графа

Граф, обозначенный G, представлен набором вершин (V) или узлов, соединенных ребрами (E). Количество ребер зависит от вершин. Края могут быть направленными или ненаправленными.

В ориентированном графе узлы связаны в одном направлении. Края здесь показывают одностороннюю связь.

В неориентированном графе ребра двунаправлены, показывая двустороннюю связь.

Пример. Хорошим вариантом использования неориентированного графа является алгоритм предложения друзей в Facebook. Пользователь (узел) имеет ребро, ведущее к другу A (другому узлу), который, в свою очередь, соединен (или имеет ребро) с другом B. Затем пользователю предлагается друг B.

Есть много других сложных типов графов, которые попадают в разные подмножества. Например, ориентированный граф имеет компоненты сильной связности, когда каждая вершина достижима из любой другой вершины.

Vertex

Вершина — это точка пересечения нескольких прямых. Его еще называют узлом.

Edge

Ребро — это математический термин, используемый для линии, соединяющей две вершины. Из одной вершины можно образовать множество ребер. Однако без вершины не может быть образовано ребро. T здесь должна быть начальной и конечной вершинами для каждого ребра.

Path

Путь в графе G = (V, E)G = ( V, E ) последовательность вершин v1, v2,…, vk, обладающая тем свойством, что между viv я а также vi + 1v я + 1. Мы говорим, что путь идет отv1v 1 к vkv k.

Последовательность 6,4,5,1,26,4,5,1,2 определяет путь от узла 6 к узлу 2.

Точно так же можно создать другие пути, пересекая края графа. Путь считается простым, если все его вершины разные.

Walk

Прогулки — это пути, но они не требуют последовательности отдельных вершин.

Connected graph

Граф связен, если для каждой пары вершин тыты а также vv, есть путь от тыты к vv.

Cycle

Цикл — это путь v1, v2,…, vk, для которого справедливо следующее:

• к> 2к> 2к > 2 к > 2
• Первые k − 1 вершина все разные
• v1 = vkv 1 = v k

Tree

Дерево — это связный граф, не содержащий цикла.

Loop

В графе, если ребро проведено от вершины к самому себе, это называется петлей. На иллюстрации V — вершина, ребро которой (V, V) образует петлю.

Как представлять графики в коде

Прежде чем мы перейдем к решению проблем с использованием алгоритмов графов, важно сначала узнать, как представлять графы в коде. Графы могут быть представлены в виде матрицы смежности или списка смежности.

Adjacency Matrix

Матрица смежности — это квадратная матрица, помеченная вершинами графа, и используется для представления конечного графа. Элементы матрицы указывают, является ли пара вершин смежной или нет в графе.

В представлении матрицы смежности вам нужно будет перебрать все узлы, чтобы идентифицировать их соседей.

a b c d e a 1 1 — — — b — — 1 — — c — — — 1 — d — 1 1 — —

Adjacency List

Список смежности используется для представления конечного графа. Представление списка смежности позволяет легко перебирать соседей узла. Каждый индекс в списке представляет вершину, а каждый узел, связанный с этим индексом, представляет свои соседние вершины.

1 a -> a b > 2 b -> c > 3 c -> d > 4 d -> b c >

Для базового класса графа, приведенного ниже, мы будем использовать реализацию списка смежности, поскольку она работает быстрее для решений алгоритмов, представленных далее в этой статье.

The Graph Class

Требования к реализации нашего графа довольно просты. Нам понадобятся два элемента данных: общее количество вершин в графе и список для хранения смежных вершин. Нам также нужен метод добавления ребер или набор ребер.

Источник: bestprogrammer.ru