Как рассчитать критерий манна уитни в программе статистика

Всем привет! Меня зовут Дима Лунин, я аналитик в компании Авито. В этой статье я расскажу про критерий Манна-Уитни и проблемы при его использовании.

Этот критерий очень популярен. Во многих компаниях и на обучающих курсах рассказывают про два его важных преимущества:

1. Манн-Уитни — непараметрический собрат T-test. Если данные в A/B-тесте не из нормального распределения, то T-test использовать нельзя. На помощь приходит Манн-Уитни.
2. Манн-Уитни — робастный критерий. В данных часто бывает много шумов и выбросов, поэтому T-test неприменим по соображениям мощности, чувствительности или ненормальности данных. А Манн-Уитни в этот момент отлично срабатывает и более вероятно находит статистически значимый эффект.

Если вы анализировали A/B-тест, где вас интересовал прирост или падение какой-то метрики, то наверняка использовали критерий Манна-Уитни. Я хочу рассказать про подводные камни этого критерия, и почему мы в компании его не используем. А в конце вы поймёте, откуда взялся такой холиварный заголовок 🙂

Результаты расчета критерия U Манна Уитни

План статьи такой:

1. Я теоретически покажу, что проверяет Манн-Уитни и почему это не имеет ничего общего с ростом медиан и среднего значения. А ещё развею миф, что Манн-Уитни проверяет эту гипотезу:

1. На примере искусственных и реальных данных продемонстрирую, что Манн-Уитни работает не так, как вы ожидаете. Его «преимущество» в большем числе прокрасов относительно T-test, и это — главный минус этого критерия, поскольку прокрасы ложные.
2. Расскажу про логарифмирование метрики и продемонстрирую, почему это плохая идея.
3. Покажу теоретические случаи, когда Манн-Уитни применим и его можно использовать для сравнения средних.

Отвечу на вопрос: как тогда жить и какой критерий использовать для анализа A/B-тестов.

Что проверяет критерий Манна-Уитни?

Предлагаю ответить на вопрос: можем ли мы проверять равенство средних или медиан в тесте и в контроле с помощью критерия Манна-Уитни? Или проверять, что одна выборка «не сдвинута» относительно другой выборки? Или, если на языке математики:

Например, у нас в A/B-тесте две выборки:

• U[−1, 1] — равномерное распределение от −1 до 1
• U[−100, 100] — равномерное распределение от −100 до 100

Про эти два распределения мы знаем, что у них равны средние и медианы, и что они симметричны относительно 0. Кроме того, вероятность, что сгенерированное значение в первой выборке будет больше значения во второй выборке, равна 1/2. Или, если сформулировать математически, P(T > C) = 1/2, где T и C — выборки теста и контроля.

Я хочу проверить, работает ли здесь корректно Манн-Уитни. Для этого запустим эксперимент 1000 раз и посмотрим на количество отвержений нулевой гипотезы у критерия. Подробнее про этот метод можно прочесть в моей статье про улучшение A/B тестов. Если бы критерий Манна-Уитни работал как надо и проверял одну из гипотез, то по определению уровня значимости он бы ошибался на этих тестах в 5% случаев, с некоторым разбросом из-за шума.

U-критерий МАННА-УИТНИ | АНАЛИЗ ДАННЫХ #8

Проверим корректность примера на уровне значимости для T-test критерия:

# Подключим библиотеки import scipy.stats as sps from tqdm.notebook import tqdm # tqdm – библиотека для визуализации прогресса в цикле from statsmodels.stats.proportion import proportion_confint import numpy as np # Заводим счетчики количества отвергнутых гипотез для Манна-Уитни и для t-test mann_bad_cnt = 0 ttest_bad_cnt = 0 # Прогоняем критерии 1000 раз sz = 1000 for i in tqdm(range(sz)): # Генерируем распределение test = sps.uniform(loc=-1, scale=2).rvs(1000) # U[-1, 1] control = sps.uniform(loc=-100, scale=200).rvs(1000) # U[-100, 100] # Считаем pvalue mann_pvalue = sps.mannwhitneyu(control, test, alternative=’two-sided’).pvalue ttest_pvalue = sps.ttest_ind(control, test, alternative=’two-sided’).pvalue # отвергаем критерий на уровне 5% if mann_pvalue < 0.05: mann_bad_cnt += 1 if ttest_pvalue < 0.05: ttest_bad_cnt += 1 # Строим доверительный интервал для уровня значимости критерия (или для FPR критерия) left_mann_level, right_mann_level = proportion_confint(count = mann_bad_cnt, nobs = sz, alpha=0.05, method=’wilson’) left_ttest_level, right_ttest_level = proportion_confint(count = ttest_bad_cnt, nobs = sz, alpha=0.05, method=’wilson’) # Выводим результаты print(f»Mann-whitneyu significance level: , [, ]») print(f»T-test significance level: , [, ]»)
Mann-whitneyu significance level: 0.114, [0.0958, 0.1352] T-test significance level: 0.041, [0.0304, 0.0551]

T-test здесь корректно работает: он ошибается в 5% случаев, как и заявлено. А значит, пример валиден.

Манн-Уитни ошибается в 11% случаев. Если бы он проверял равенство средних, медиан или P(T > C) = 1/2, то должен был ошибиться только в 5%, как T-test. Но процент ошибок оказался в два раза больше. А значит, что эти гипотезы неверны для Манна-Уитни:

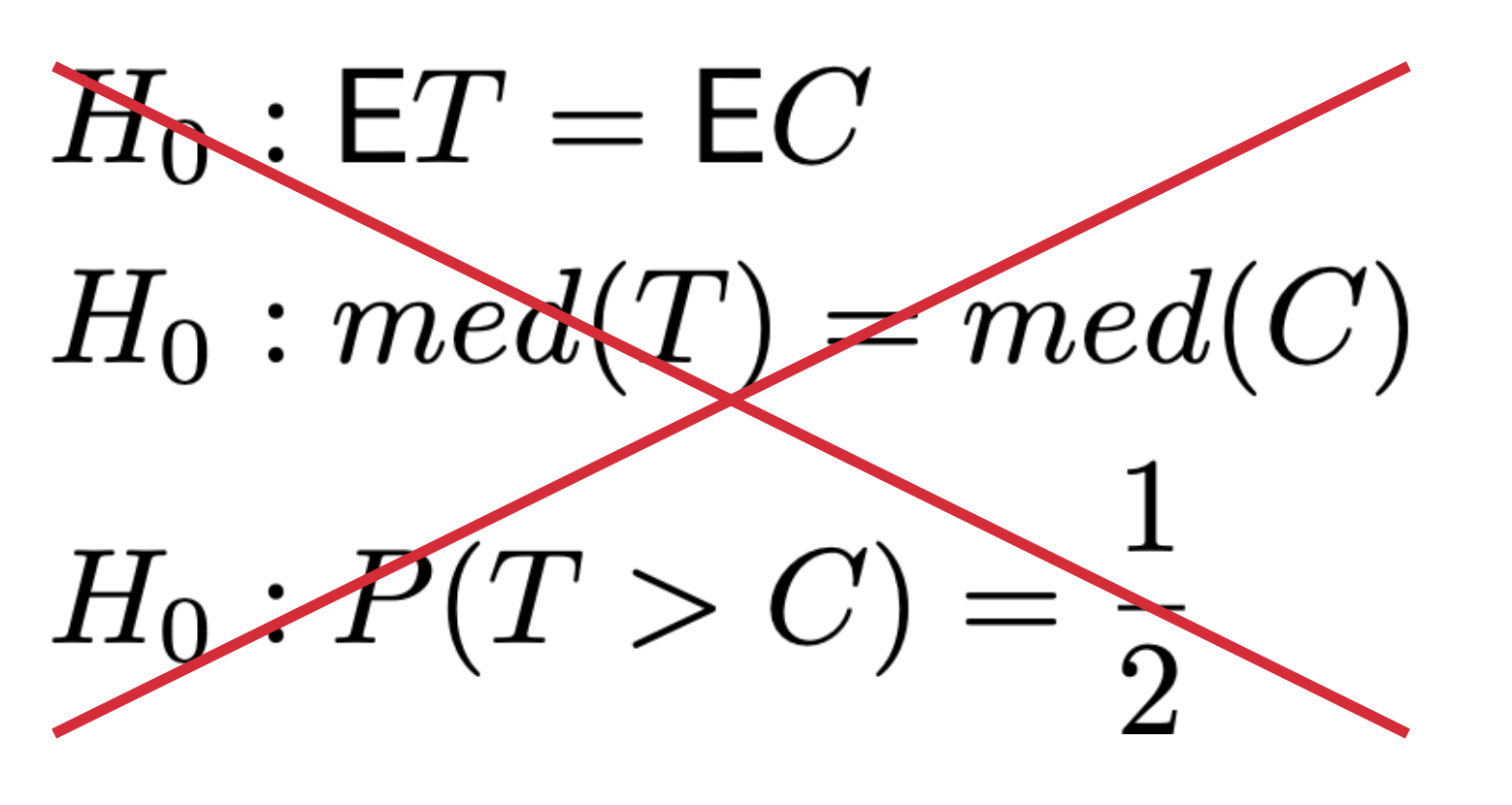
Этот метод можно использовать для проверки только такой гипотезы:

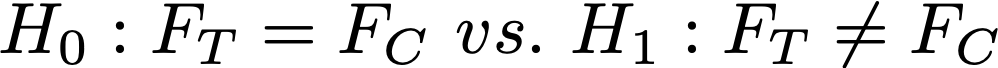
Этот критерий проверяет, что выборки теста и контроля взяты из одного распределения. Если он считает, что выборки из разных распределений — отвергает гипотезу. Это обычный критерий однородности.

Для демонстрации корректности я предлагаю снова запустить 1000 раз тесты, но выборки теста и контроля в этот раз взяты из одного распределения: U[-100, 100] (равномерное распределение от -100 до 100).

# Подключим библиотеки import scipy.stats as sps from tqdm.notebook import tqdm # tqdm – библиотека для визуализации прогресса в цикле from statsmodels.stats.proportion import proportion_confint import numpy as np # Заводим счетчики количества отвергнутых гипотез для Манна-Уитни и для t-test mann_bad_cnt = 0 ttest_bad_cnt = 0 # Прогоняем критерии 1000 раз sz = 1000 for i in tqdm(range(sz)): # Генерируем распределение test = sps.uniform(loc=-100, scale=200).rvs(1000) # U[-100, 100] control = sps.uniform(loc=-100, scale=200).rvs(1000) # U[-100, 100] # Считаем pvalue mann_pvalue = sps.mannwhitneyu(control, test, alternative=’two-sided’).pvalue ttest_pvalue = sps.ttest_ind(control, test, alternative=’two-sided’).pvalue # отвергаем критерий на уровне 5% if mann_pvalue < 0.05: mann_bad_cnt += 1 if ttest_pvalue < 0.05: ttest_bad_cnt += 1 # Строим доверительный интервал для уровня значимости критерия (или для FPR критерия) left_mann_level, right_mann_level = proportion_confint(count = mann_bad_cnt, nobs = sz, alpha=0.05, method=’wilson’) left_ttest_level, right_ttest_level = proportion_confint(count = ttest_bad_cnt, nobs = sz, alpha=0.05, method=’wilson’) # Выводим результаты print(f»Mann-whitneyu significance level: , [, ]») print(f»T-test significance level: , [, ]»)
Mann-whitneyu significance level: 0.045, [0.0338, 0.0597] T-test significance level: 0.043, [0.0321, 0.0574]

Манн-Уитни не может проверить ничего, кроме равенства распределений. Этот критерий не подходит для сравнения средних или медиан.

Разберёмся, почему Манна-Уитни нельзя применять для сравнения средних, медиан и P(T > C) = 1/2. Для начала посмотрим на статистику, которая считается внутри критерия:

Для неё считаются те критические области, при попадании в которые статистики U критерий отвергнется.

Отсюда видно, что:

1. Манн-Уитни учитывает расположение элементов выборок относительно друг друга, а не значения элементов. Поэтому он не может сравнивать математические ожидания, если он даже не знает абсолютные значения элементов выборки.
2. Гипотеза H_0: P(T > C) = 1/2 неверна для данного критерия. Если P(T > C) = 1/2, то мат. ожидание EU = (произведение размера выборок) / 2. Но при равенстве распределений мат ожидание статистики U будет точно таким же. Почему критерий не сработал на примере с 2 разными равномерными распределениями U[-1, 1] VS U[-100, 100], но сработал при сравнении распределений U[-100, 100] VS U[-100, 100]? Суть в том, что мы не знаем распределение статистики U. Когда тест и контроль из одного распределения, мы знаем, что статистика U распределена нормально. Но если это не так, то теорема перестаёт работать. Тогда мы не знаем, как распределена статистика U, и не можем посчитать p-value.
3. По этой же причине критерий не может проверять равенство медиан.

U-критерий Манна-Уитни в дипломной, курсовой и магистерской работе по психологии

Подавляющее большинство психологических исследований направлены на достижение двух главных целей:

1. Выявить взаимосвязь между показателя. Для этого используется корреляционный анализ.
2. Установить различия выраженности психологических показателей в двух или более группах. В этом случае используются либо U-критерий Манна-Уитни, либо t-критерий Стъюдента.

В данной статье мы рассмотрим основные аспекты использования критерия Манна-Уитни при обработке результатов эмпирического исследования в курсовых и дипломных работах, а также магистерских диссертациях по психологии.

Зачем нужен критерий Манна-Уитни

В психологическом исследовании изучаются не результаты отдельных испытуемых, а обобщенные данные. Например, при изучении особенностей психологических параметров в двух группах изучаются средние значения в этих группах.

Напомним, что среднее (среднее арифметическое) отражает усредненный по группе показатель. Рассчитывается среднее значение следующим образом:

• Суммируются показатели у всех испытуемых в группе.
• Сумма делиться на число испытуемых.

Таким образом, когда мы сравниваем психологические показатели у двух испытуемых, то никакие статистические критерии не нужны. Действительно, пусть в ходе тестирования уровень личностной тревожности Иванова оказался 40 баллов, а Петрова – 50 баллов. В этом случае мы смело говорим, что Петров более тревожен, чем Иванов. Однако, если речь идет о сравнении двух групп, то ситуация усложняется.

Например, мы рассчитали средний уровень личностной тревожности в группе женщин – 58 баллов, и мужчин – 49 баллов. Так как средние значения – это статистические показатели, а не просто числа, то просто так сравнивать их нельзя. То есть, мы не можем сказать, что тревожность женщин выше, чем у мужчин. Но как же быть? Как сравнить показатели тревожности в группах мужчин и женщин?

Для этого и существуют статистические критерии анализа различий. Их расчет позволяет с определённой точностью заключить, существуют различия выраженности показателей в двух группах или нет.

Для анализа различий средних значений в двух группах используется t-критерий Стъюдента. U-критерий Манна-Уитни позволяет сравнивать не средние значения, а выраженность показателей, но в этом случае и средние значения параметров в группах будут различаться соответствующим образом.

Расчет критерия Манна-Уитни: объяснение простыми словами

В подавляющем большинство психологических исследований расчет статистических критериев в том числе и критерия Манна-Уитни производится с помощью статистических программ. Наиболее известные – это SPSS и STATISTICA. Однако несмотря на это важно в общих чертах представлять себе сущность расчета – это придаст студенту-психологу на защите диплома.

Вернёмся к нашему пример с тревожностью мужчин и женщин. Предположим у нас две группы по 10 человек. У каждого испытуемого есть определенное значение личностной тревожности. Нам нужно выяснить, различаются ли уровни тревожности в группах мужчин и женщин. Расчет критерия Манна-Уитни примерно будет проходить по следующим шагам:

1. Показатели тревожности в группах заносятся в таблицу ранжируются, то есть располагаются в порядке возрастания.
2. Далее данные по мужчинам женщинам объединяются в общий столбец (при этом они помечаются, например, разными цветом) и опять ранжируются.
3. А далее проводится анализ. Если данные мужчин и женщин (синие и красные числа) в основном чередуются, то различий скорее всего нет.
4. А вот если данные по мужчинам сгруппированы в основном вверху, где низкие показатели, а у женщин внизу, где высокие, то скорее всего различия есть.

критерий манна уитни. U критерий Манна-Уитни. Теоретическая часть Зачем нужен критерий МаннаУитни

Единственный в мире Музей Смайликов

Самая яркая достопримечательность Крыма

Скачать 48.15 Kb.

Теоретическая часть

Зачем нужен критерий Манна-Уитни

• Суммируются показатели у всех испытуемых в группе.
• Сумма делиться на число испытуемых.

Например, мы рассчитали средний уровень личностной тревожности в группе женщин – 58 баллов, и мужчин – 49 баллов. Так как средние значения – это статистические показатели, а не просто числа, то просто так сравнивать их нельзя. То есть, мы не можем сказать, что тревожность женщин выше, чем у мужчин. И как же быть? Как сравнить показатели тревожности в группах мужчин и женщин?

Для этого и существуют статистические критерии анализа различий. Их расчет позволяет с определённой точностью заключить, существуют различия выраженности показателей в двух группах или нет.

Расчет критерия Манна-Уитни: объяснение простыми словами

1. Показатели тревожности в группах заносятся в таблицу и ранжируются, то есть располагаются в порядке возрастания.
2. Далее данные по мужчинам и женщинам объединяются в общий столбец (при этом они помечаются, например, разными цветом) и опять ранжируются.
3. А далее проводится анализ. Если данные мужчин и женщин (синие и красные числа) в основном чередуются, то различий скорее всего нет.
4. А вот если данные по мужчинам сгруппированы в основном вверху, где низкие показатели, а у женщин внизу, где высокие, то скорее всего различия есть.

Что нужно знать про критерий Манна-Уитни, если вы им воспользуетесь на защите диплома

Что такое непараметрический? Я напомню, что здесь нужно понимать следующее: Параметрические статистические критерии более точные, но они предъявляют более строгие требования к данным. То есть, перед расчетом нужно все данные в группах проверять, например, на нормальность распределения. Это значит, что на графике распределения такие данные должны располагаться в виде колокола – больше всего испытуемых со средними значениями, а меньшинство имеют низкие и высокие показатели. t-критерий Стъюдента, с которым вы уже знакомы, является параметрическим критерием.

Непараметрические критерии менее точные, но зато у них нет жестких требований к данным. Эти данные могут быть почти любыми.

Ограничения критерия Манна-Уитни

1. Число испытуемых в группах при использовании критерия Манна-Уитни не должно быть больше 60 человек.
2. Минимальное число испытуемых – 3 человека в каждой группе.
3. Объем групп не должен быть строго одинаковым, но не должен сильно различаться.
4. Сравниваемые показатели могут быть как психологическими (тревожность, агрессивность, самооценка и пр.), так и не психологическими (успешность обучения, эффективность профессиональной деятельности и пр.)

Если вам зададут вопрос: «Почему вы выбрали для расчета критерий Манна-Уитни, а не критерий Стьюдента?»

«В данной работе не проверялись данные на нормальность распределения, поэтому использовался непараметрический статистический критерий Манна-Уитни, предназначенный для выявления различий показателей в двух несвязных выборках».

Уровень статистической значимости

1. U – это, собственно, численное значение критерия. Для определения достоверности различий выраженности показателей в группах нужно сравнить полученное значение Uэмп с критическим значением из специальной таблицы – Uкр. Если Uэмп ≤ Uкр, то различия выраженности показателей в группах статистически значимы.
2. р – уровень статистической значимости. Этот показатель присутствует при расчете всех статистических критериев и отражает степень точности вывода о наличие различий. Напоминаю, что в психологических исследованиях приняты два уровня точности:

• р≤0,01 – вероятность ошибки 1%;
• р≤0,05 – вероятность ошибки 5%.

Пример анализа данных с помощью критерия Манна-Уитни

Анализ данных, приведенных в таблице по среднему показателю и по U-критерию, позволяет сделать следующие выводы:

Показатели по шкале «вовлеченность» в группе представителей старшего поколения статистически значимо выше, чем в группе представителей молодежи. Люди зрелого возраста характеризуются более высокой вовлеченностью в происходящее, они в большей степени получают удовольствие от собственной деятельности. В то же время молодежь в большей степени переживает чувство отвергнутости, ощущение себя «вне» жизни. Такой результат связан с психологическими особенностями возрастов: молодые люди еще не нашли своего места в жизни, это обуславливает их недостаточную вовлеченность в происходящее. Зрелые же люди в значительной степени укоренились в жизни, что позволяет им быть на более высоком уровне вовлеченности.

Показатели по шкале «принятие риска» в группе молодежи статистически значимо выше, чем в группе представителей зрелого возраста. Это означает, что молодые люди характеризуются более высокой убежденностью в том, что все то, что с ним случается, способствует его развитию за счет знаний, извлекаемых из опыта. Молодые в больше степени, чем зрелые люди, рассматривают жизнь как способ приобретения опыта, готовы действовать в отсутствие надежных гарантий успеха, на свой страх и риск, считая стремление к простому комфорту и безопасности обедняющим жизнь личности.

Как показывают полученные данные, различия показателей жизнестойкости в группах представителей молодежи и людей зрелого возраста не являются статистически значимыми, что в итоге предопределяет отсутствие различий в общем показателей жизнестойкости в группах испытуемых.

Различия показателей жизнестойкости в группах представителей молодого поколения и людей зрелого возраста носят разнонаправленный характер, так как зона пересечения показателей, что оценивает U-критерий, у этих групп незначительная, и это говорит о том, что у молодежи в большей степени выражено принятие риска, а у людей зрелого возраста – вовлеченность в происходящее.
Практическая часть

Назначение критерия. Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. Он позволяет выявлять различия между малыми выборками, когда n₁,n₂ ≥3 или n₁= 2, n₂ ≥ 5, и является более мощным, чем критерий Q Розенбаума.

Описание критерия. Этот метод определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами. Мы помним, что 1ым рядом (выборкой, группой) мы называем тот ряд значений, в котором значения, по предварительной оценке, выше, а 2ым рядом — тот, где они предположительно ниже.

Гипотезы.

Н1: Уровень признака в группе 2 ниже уровня признака в группе 1.

Некоторые возможные представление критерия U.

Рассмотрим три из множества возможных вариантов соотношения двух рядов значений.

а). 2й ряд ниже первого, но ряды почти не перекрещиваются. Область наложения слишком мала (они практически различны и количество совпадений очень мало), чтобы скрадывать различия между рядами. Есть шанс, что различия между ними достоверны. Точно определить это мы сможем с помощью критерия U.

б). 2ой ряд тоже ниже первого, но область перекрещивающихся значений у двух рядов достаточно обширна. Она может еще не достигать критической величины, когда различия придется признать несущественными. Но так ли это, можно определить только путем точного подсчета критерия U.

в). 2ой ряд ниже первого, но область наложения настолько обширна, что различия между рядами скрадываются.

1. В каждой выборке должно быть не менее 3 наблюдений: n1,п2≥ 3; допускается, чтобы в одной выборке было 2 наблюдения, но тогда во 2ой их должно быть не менее 5.
2. В каждой выборке должно быть не более 60 наблюдений; п1, п2≤ 60. Однако уже при

Рассмотрим результатам обследования студентов физического и психологического факультетов Ленинградского университета с помощью методики Д. Векслера для измерения невербального интеллекта.

Данные приведены в таблице 1.

Индивидуальные значения невербального интеллекта

в выборках студентов физического (n1=14)

Правила ранжирования

1. Меньшему значению начисляется меньший ранг. Наименьшему значению начисляется ранг 1.

Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений. Например, если n=7, то наибольшее значение получит ранг 7, за возможным исключением для тех случаев, которые предусмотрены правилом 2.

2. В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны.

Например, 3 наименьших значения равны 10 секундам. Если бы мы измеряли время более точно, то эти значения могли бы различаться и составляли бы, скажем, 10,2 сек; 10,5 сек; 10,7 сек. В этом случае они получили бы ранги, соответственно, 1, 2 и 3. Но поскольку полученные нами значения равны, каждое из них получает средний ранг: (1+2+3)/3 = 6/3 = 2

Допустим, следующие 2 значения равны 12 сек. Они должны были бы получить ранги 4 и 5, но, поскольку они равны, то получают средний ранг: (4+5)/2 = 9/2 = 4,5 и т.д.

3. Общая сумма рангов должна совпадать с расчетной, которая определяется по формуле:

где N — общее количество ранжируемых наблюдений (значений). Несовпадение реальной и расчетной сумм рангов будет свидетельствовать об ошибке, допущенной при начислении рангов или их суммировании. Прежде чем продолжить работу, необходимо найти ошибку и устранить ее.

При подсчете критерия U легче всего сразу приучить себя действовать по строгому алгоритму.

Подсчет критерия U Манна-Уитни.