
– это критерий, который используется для сравнения двух и более относительных показателей, характеризующих частоту определенного признака, имеющего два значения. Исходные данные для расчета точного критерия Фишера обычно группируются в виде четырехпольной таблицы, но могут быть представлены и многопольной таблицей.
1. История разработки критерия
Впервые критерий был предложен Рональдом Фишером в его книге «Проектирование экспериментов». Это произошло в 1935 году. Сам Фишер утверждал, что на эту мысль его натолкнула Муриэль Бристоль. В начале 1920-х годов Рональд, Муриэль и Уильям Роуч находились в Англии на опытной сельскохозяйственной станции.
Муриэль утверждала, что может определить, в какой последовательности наливали в ее чашку чай и молоко. На тот момент проверить правильность ее высказывания не представлялось возможным.
Это дало толчок идее Фишера о «нуль гипотезе». Целью стала не попытка доказать, что Муриэль может определить разницу между по-разному приготовленными чашками чая. Решено было опровергнуть гипотезу, что выбор женщина делает наугад. Было определено, что нуль-гипотезу нельзя ни доказать, ни обосновать. Зато ее можно опровергнуть во время экспериментов.
Критерий Фишера для проверки адекватности построенной регрессии
Было приготовлено 8 чашек. В первые четыре налито молоко сначала, в другие четыре – чай. Чашки были помешаны. Бристоль предложили опробовать чай на вкус и разделить чашки по методу приготовления чая. В результате должно было получиться две группы.
История говорит, что эксперимент прошел удачно.
Благодаря тесту Фишера вероятность того, что Бристоль действует интуитивно, была уменьшена до 0.01428. То есть, верно определить чашку можно было в одном случае из 70. Но все же нет возможности свести к нулю шансы того, что мадам определяет случайно. Даже если увеличивать число чашек.
Эта история дала толчок развитию «нуль гипотезы». Тогда же был предложен точный критерий Фишера, суть которого в переборе всех возможных комбинаций зависимой и независимой переменных.
2. Для чего используется точный критерий Фишера?
Точный критерий Фишера в основном применяется для сравнения малых выборок. Этому есть две весомые причины. Во-первых, вычисления критерия довольно громоздки и могут занимать много времени или требовать мощных вычислительных ресурсов. Во-вторых, критерий довольно точен (что нашло отражение даже в его названии), что позволяет его использовать в исследованиях с небольшим числом наблюдений.
Особое место отводится точному критерию Фишера в медицине. Это важный метод обработки медицинских данных, нашедший свое применение во многих научных исследованиях. Благодаря ему можно исследовать взаимосвязь определенных фактора и исхода, сравнивать частоту патологических состояний между разными группами пациентов и т.д.
3. В каких случаях можно использовать точный критерий Фишера?
- Сравниваемые переменные должны быть измерены в номинальной шкале и иметь только два значения, например, артериальное давление в норме или повышено, исход благоприятный или неблагоприятный, послеоперационные осложнения есть или нет.
- Критерий подходит для сравнения очень малых выборок: точный критерий Фишера может применяться для анализа четырехпольных таблиц в случае значений ожидаемого явления менее 10, что является ограничением для применения критерия хи-квадрат Пирсона.
- Точный критерий Фишера бывает односторонним и двусторонним. При одностороннем варианте точно известно, куда отклонится один из показателей. Например, во время исследования сравнивают, сколько пациентов выздоровело по сравнению с группой контроля. Предполагают, что терапия не может ухудшить состояние пациентов, а только либо вылечить, либо нет.
Двусторонний тест является предпочтительным, так как оценивает различия частот по двум направлениям. То есть оценивается верятность как большей, так и меньшей частоты явления в экспериментальной группе по сравнению с контрольной группой.
Расчет точного теста Фишера в excel
Аналогом точного критерия Фишера является Критерий хи-квадрат Пирсона, при этом точный критерий Фишера обладает более высокой мощностью, особенно при сравнении малых выборок, в связи с чем в этом случае обладает преимуществом.
4. Как рассчитать точный критерий Фишера?
Допустим, изучается зависимость частоты рождения детей с врожденными пороками развития (ВПР) от курения матери во время беременности. Для этого выбраны две группы беременных женщин, одна из которых — экспериментальная, состоящая из 80 женщин, куривших в первом триместре беременности, а вторая — группа сравнения, включающая 90 женщин, ведущих здоровый образ жизни на протяжении всей беременности. Число случаев ВПР плода в экспериментальной группе составило 10, в группе сравнения — 2.
Вначале составляем четырехпольную таблицу сопряженности:
| Исход есть (Наличие ВПР) | Исхода нет (Отсутствие ВПР) | Всего | |
| Фактор риска есть (Курящие) | A = 10 | B = 70 | (A + B) = 80 |
| Фактор риска отсутствует (Некурящие) | C = 2 | D = 88 | (C + D) = 90 |
| Всего | (A + C) = 12 | (B + D) = 158 | (A + B + C + D) = 170 |
Точный критерий Фишера рассчитывается по следующей формуле:
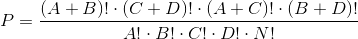
где N — общее число исследуемых в двух группах; ! — факториал, представляющий собой произведение числа на последовательность чисел, каждое из которых меньше предыдущего на 1 (например, 4! = 4 · 3 · 2 · 1)
В результате вычислений находим, что P = 0,0137.
5. Как интерпретировать значение точного критерия Фишера?
Достоинством метода является соответствие полученного критерия точному значению уровня значимости p. То есть, полученное в нашем примере значение 0,0137 и есть уровень значимости различий сравниваемых групп по частоте развития ВПР плода. Необходимо лишь сопоставить данное число с критическим уровнем значимости, обычно принимаемым в медицинских исследованиях за 0,05.
- Если значение точного критерия Фишера больше критического, принимается нулевая гипотеза и делается вывод об отсутствии статистически значимых различий частоты исхода в зависимости от наличия фактора риска.
- Если значение точного критерия Фишера меньше критического, принимается альтернативная гипотеза и делается вывод о наличии статистически значимых различий частоты исхода в зависимости от воздействия фактора риска.
Источник: medstatistic.ru
F-критерий Фишера для таблиц сопряжённости
Нередко на практике встречаются задачи, когда нужно обнаружить или опровергнуть связи между нечисловыми данными. Например, выяснить, влияет ли наличие работы в выходные дни на вероятность развития выгорания.
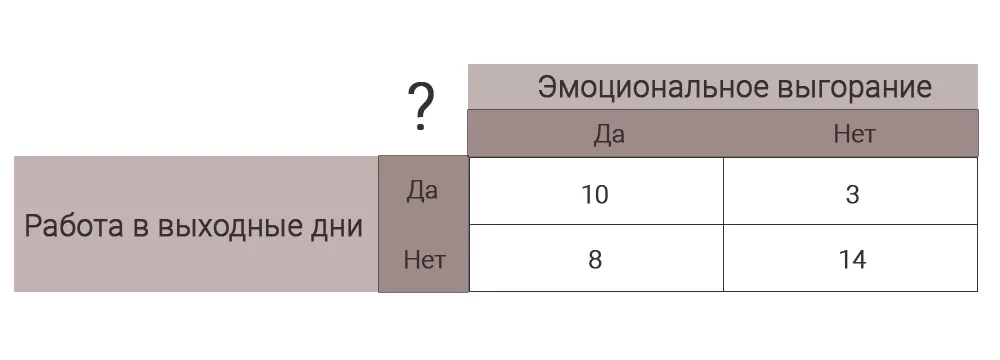
Для решения подобных задач применяют критерий Фишера. Рассмотрим, кто впервые заговорил об этом критерии, где в современном мире он нашёл применение и каковы условия его применения.
Точный критерий Фишера – это критерий, используемый для сравнения 2-х независимых выборок по качественному (номинальному) признаку.
Критерий был предложен в 1935 году английским статистиком, биологом-эволюционистом и генетиком Рональдом Фишером. Об этом он упомянул в своей книге «Проектирование экспериментов» после того, как совместно с коллегами, провёл эксперимент с чашками молока и чая, находясь на английской станции сельского хозяйства. Именно это событие стало ключевым в развитии «нуль гипотезы».
Применение критерия
Точный критерий Фишера нашёл своё место преимущественно в медицине и психологии. Благодаря ему исследуются взаимосвязи определенных фактора и исхода:
- Связан ли пол с развитием заболевания X?
- Существует ли статистически значимая связь между курением и профессиональным спортом?
- Приводят ли определенные методы лечения рака к хорошим результатам?
- Существенно ли отличаются две лечебные группы по скорости выздоровления от болезни?
Условия применения критерия Фишера:
- Две переменные являются категориальными (номинальными)
- Выборки независимы (две группы никак не связаны между собой)
Точный критерий Фишера в основном используют в исследованиях с небольшим числом наблюдений, ввиду его высокой точности и громоздкости вычислений.
Как вычислить точный критерий Фишера
Для начала необходимо составить четырехпольную таблицу сопряженности, после – рассчитать критерий Фишера по формуле, вручную или через статистические программы.
Как выполнить точный тест Фишера в Stata
Точный критерий Фишера используется для определения того, существует ли значительная связь между двумя категориальными переменными. Обычно он используется в качестве альтернативы критерию независимости хи-квадрат, когда количество одной или нескольких ячеек в таблице 2 × 2 меньше 5.
В этом руководстве объясняется, как выполнить точный тест Фишера в Stata.
Пример: точный критерий Фишера в Stata
Предположим, мы хотим знать, связан ли пол с предпочтениями политической партии в конкретном колледже. Чтобы изучить это, мы случайным образом опрашиваем 25 студентов в кампусе. Количество студентов, которые являются демократами или республиканцами, в зависимости от пола, показано в таблице ниже:
| | демократ | республиканец | | — | — | — | | Мужской | 4 | 9 | | женский | 8 | 4 |
Чтобы определить, существует ли статистически значимая связь между полом и предпочтениями политической партии, мы можем выполнить точный тест Фишера.
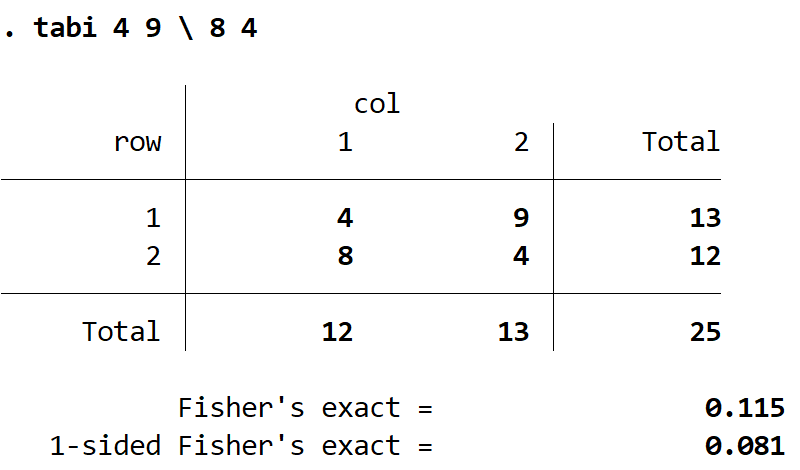
В Stata мы можем использовать команду tabi для выполнения точного теста Фишера. Мы вводим подсчеты в таблицу 2×2 слева направо с помощью ** , чтобы разделить верхнюю и нижнюю строки.
таби 4 9 8 4
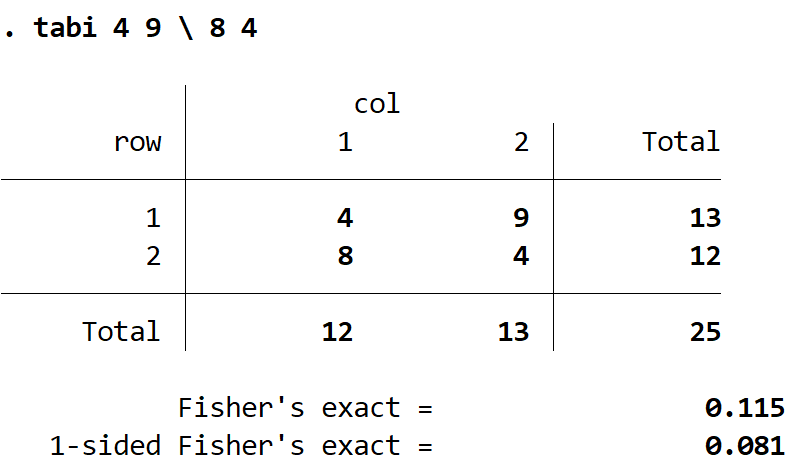
Вот как интерпретировать вывод:
Выходная таблица: эта таблица показывает количество для каждой ячейки, как мы их ввели.
Точность Фишера: это значение p, связанное с двусторонним точным критерием Фишера. В данном случае это 0,115.
Односторонний точный критерий Фишера: это значение p, связанное с односторонним точным критерием Фишера. В данном случае это 0,081.
Нулевая гипотеза для точного теста Фишера состоит в том, что две переменные независимы. В этом случае наша нулевая гипотеза состоит в том, что пол и предпочтение политической партии независимы, что является двусторонним тестом, поэтому мы будем использовать первое значение p, равное 0,115.
Поскольку это значение p не менее 0,05, мы не отвергаем нулевую гипотезу. Таким образом, у нас нет достаточных доказательств, чтобы сказать, что существует значительная связь между полом и предпочтениями политических партий.
Источник: www.codecamp.ru