Как работать в программе статистика 13

В версии Statistica 13 был обновлен интерфейс системы. Иконки получили цветовой код в зависимости от их функционала.

Компоненты для доступа к входным данным; настройки Таблиц

Аналитические процедуры обучения/использования моделей

Компоненты, не относящиеся к другим группам

Компоненты, связанные с созданием Отчетов и Сохранением данных

Компоненты, связанные с продуктами Enterprise Server и MAS

Часть I. Знакомство с SPSS

Управление данными; преобразование данных

Workspace

Управление аналитическим процессом с помощью интерфейса Workspace стало доступно всем пользователям Statistica.

Статистика. Lab1. Ввод и предварительный анализ данных в Statistic

Была создана дополнительная таблица с помощью команды «Замер подмножества/Случайный замер». Затем выполнен переход к переменной ln(РОСТ) и обратно:

Нормировка количественных признаков используется для приведения их к стандартному виду, удобному для обработки. Обычно при расчёте расстояния между объектами нормируют признаки, измеренные в разнородных физический единицах.

В Statistica значения переменных изменяются по формуле:

Новое значение = (Старое значение — Среднее)/Стандартное отклонение

1. Сортировка данных. Команда «Сортировка».

Данные, отсортированные по полу и внутри пола по убыванию роста:

Работа с данными в системе Statistica

NТаблица с переменной СРБАЛЛ:

Предварительный анализ данных. Визуализация данных.

1. Проекция данных на один признак

Как установить Statistica 12 на Windows 10 | 7

Средний рост человека между 176 и 178.

Средний вес человека между 60 и 65.

3. Проекция на плоскость двух признаков – двумерная диаграмма рассеяния.

Сомнительные точки 178,62 и 179, 93.

Сомнительная тачка: 75,71.

1. проекция на плоскость трех признаков – объемная диаграмма рассеяния.

Генерация случайных чисел в Statistica

Исследование зависимости стандартной ошибки выборочного среднего и выборочной дисперсии от объёма выборки:

Как видно стандартное ошибка среднего в √N=10 раз меньше стандартного отклонения

Гистограммы выборочного среднего и выборочного стандартного отклонения:

Исследование влияния объёма выборки на достоверность результатов статистического анализа:

Как видно из графиков при увеличении объёма выборки значение ошибки уменьшается, а при увеличении числа признаков увеличивается.

Источник: urvanov.ru

0. 1-13 Статистика. Программа статистического исследования Статистика

Единственный в мире Музей Смайликов

Самая яркая достопримечательность Крыма

Скачать 3.77 Mb.

1. Методика статистического исследования
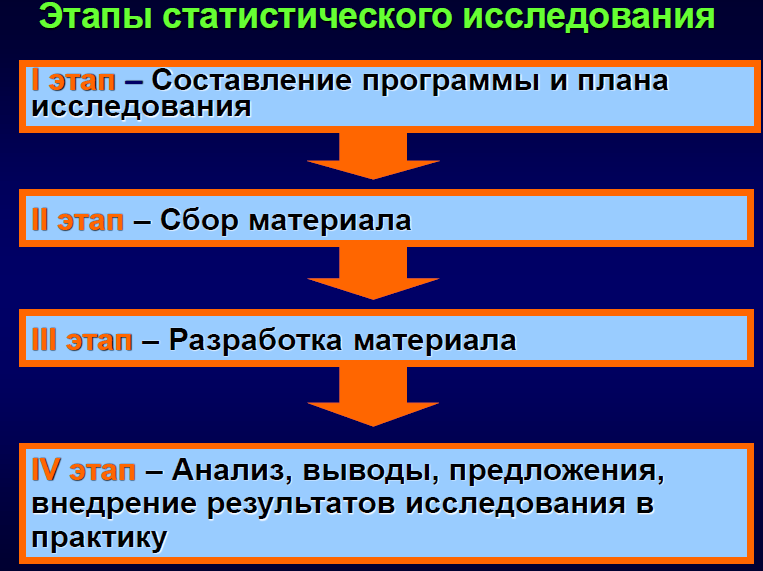
2. Этапы статистического исследования
3. План и программа статистического исследования

4. Абсолютные и относительные величины

1. абсолютными,
2. относительными,
3. средними.

Абсолютные величины – это показатели, выражающие размеры общественных явлений и процессов. По способу выражения этих размеров они подразделяются на индивидуальные и суммарные (итоговые).

Индивидуальные абсолютные величины – это показатели, выражающие размеры количественных признаков у отдельных единиц исследуемых объектов, например, температура тела у конкретного больного, количество больных, принятых врачом за смену.

Суммарные абсолютные показатели дают ответ на поставленный вопрос о сумме единиц наблюдения среды или изучаемого по программе исследования явления. Получаются они в результате непосредственного подсчета единиц наблюдения или суммирования значений количественных признаков, которыми обладают эти единицы. Так, подсчет больниц по данным годовых отчетов дает их численность, а суммирование их коечного фонда – показатель абсолютного его размера (количество больничных коек в крае).

Абсолютные величины служат основой для вычисления относительных и средних величин (например, количество обслуженных вызовов за день, число зарегистрированных заболеваний за год на территории обслуживания поликлиники и др.). Абсолютные величины представлены в учетных (Листок учета врача-стоматолога, Дневник работы врача поликлиники) и отчетных статистических формах.

Хотя абсолютные величины при анализе чаще имеют ограниченное познавательное значение, т.к. по ним трудно судить о частоте, динамике какого-либо явления или дать оценку работы врачей или подразделения.

Для определения структуры и уровня изучаемого явления, сравнения его в динамике или у различных групп населения, или по отдельным административным территориям пользуются относительными величинами.

Относительные величины (коэффициенты) – выражают количественные соотношения, присущие общественным явлениям и процессам. Получаются они как результат сравнения (отношения, деления) двух абсолютных величин. С относительными величинами мы сталкиваемся в основном при анализе состояния здоровья населения и при анализе деятельности учреждений здравоохранения по данным годового отчета.

Средние величины – характеризуют средний уровень изучаемого признака.

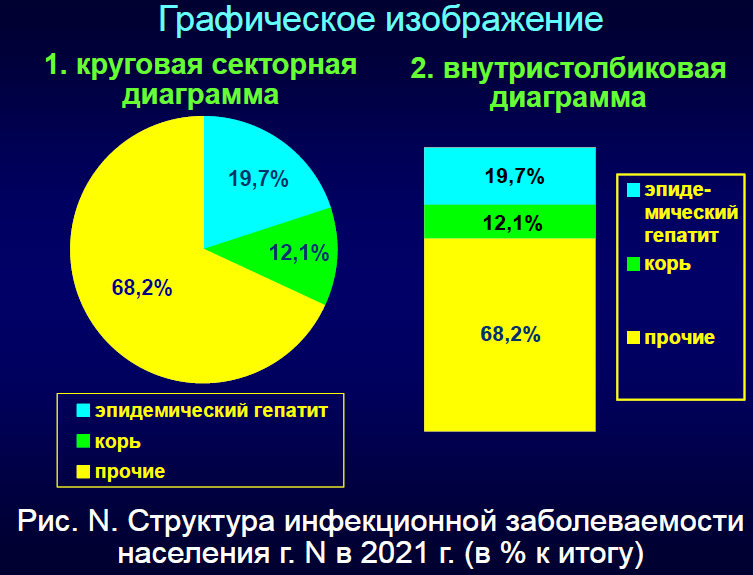
При расчете этого показателя следует помнить о следующих требованиях:

1. желательно, чтобы показатель получился целым числом (это облегчает логическое осмысление показателя), отсюда и величина цифры, на которую умножают, т.е. стандарта – 100, 1000, 10 000 и 100 000;
2. сопоставлять можно только те показатели, которые рассчитаны на один и тот же стандарт. Вместе с тем, общепринято, что на 100 вычисляются показатели летальности, заболеваемости с временной утратой трудоспособности, патологической пораженности; на 1000 – показатели общей заболеваемости, выявляемости, некоторые демографические показатели; на 10 000 – показатели соотношения (обеспеченности); на 100 000 – показатель смертности по отдельным причинам. Чем реже встречается явление, тем большее число берется в качестве стандарта.

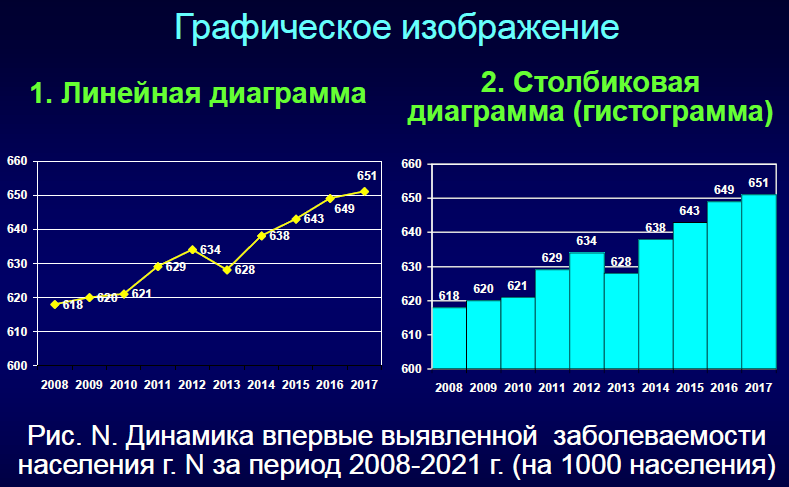
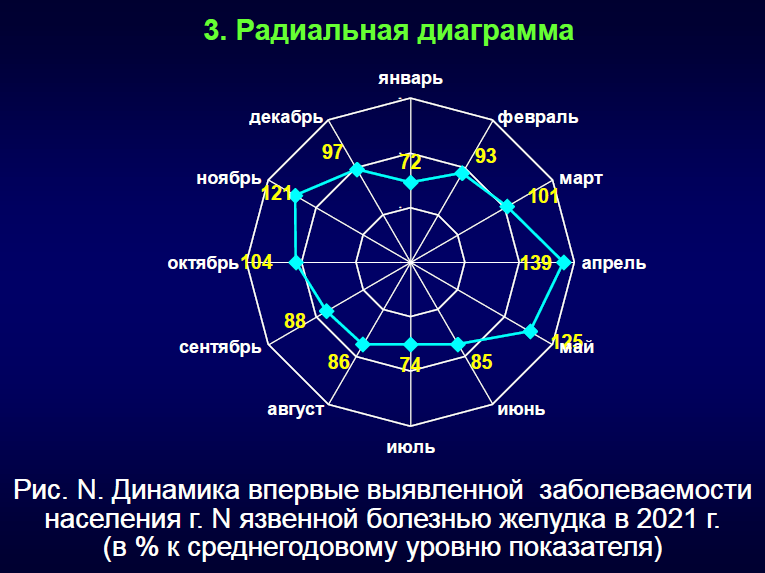
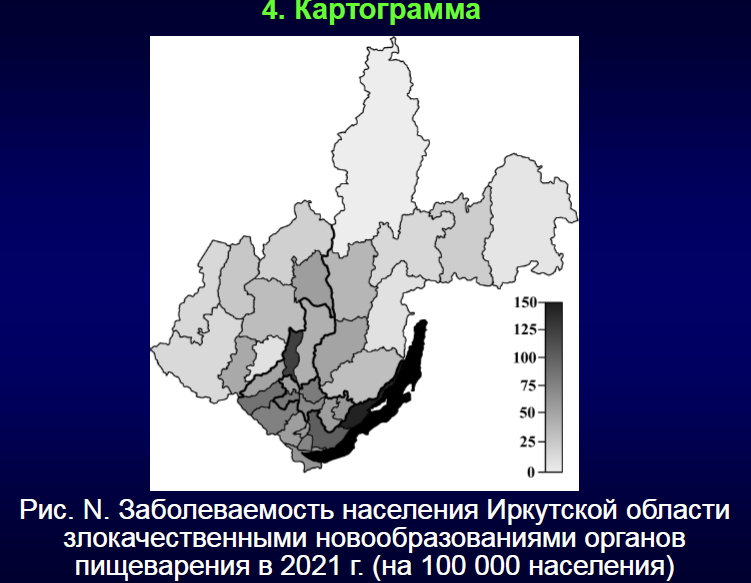
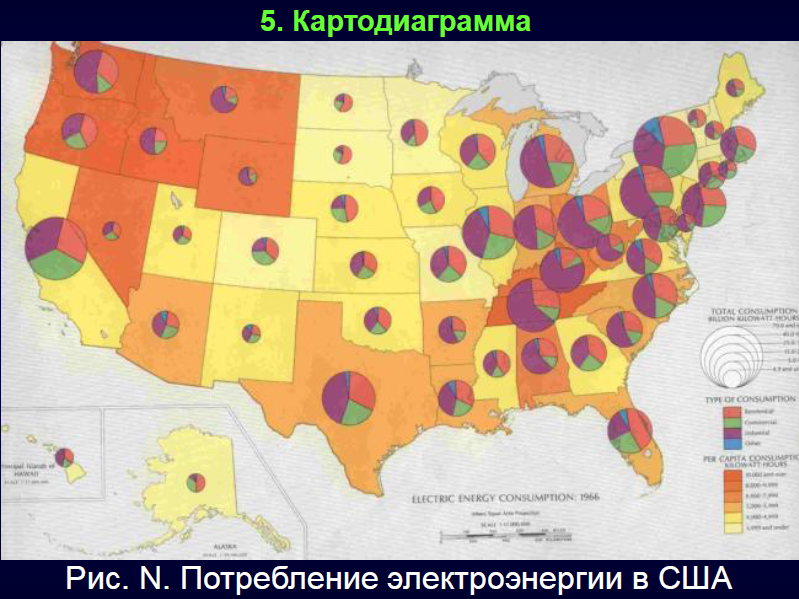
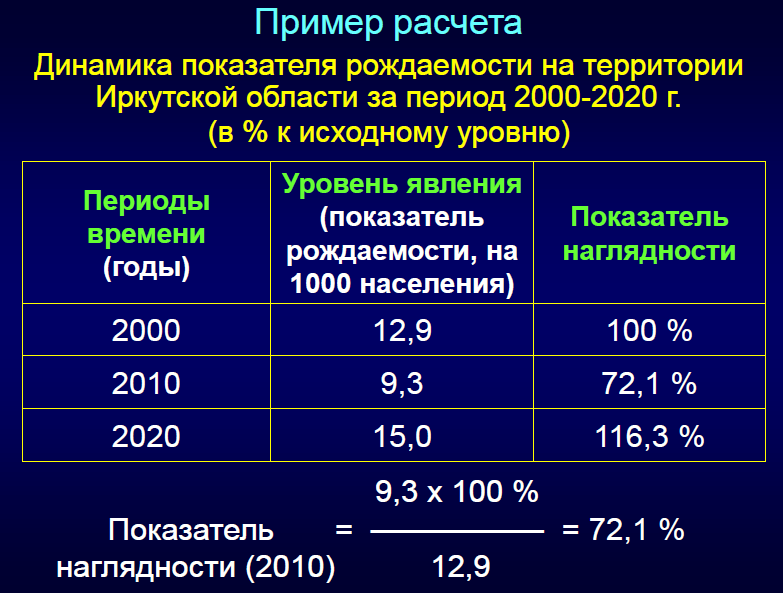
7. Динамический ряд , его анализ, применение в деятельности врача вашей специальности.

Для анализа динамики применяются динамические ряды.

Динамический ряд – это ряд, состоящий из однородных сопоставимых величин, характеризующих изменение какого-либо явления за определенный промежуток времени.

Числа, составляющие динамический ряд, принято называть уровнями (U). Уровни могут быть представлены абсолютными, относительными и средними величинами. Следует помнить, что динамический ряд должен состоять из чисел, характеризующих одно и то же явление и в одинаковых единицах измерения.

Динамический ряд не только дает возможность проанализировать динамику развития какого-либо явления, но и выявить рост и снижение его, отдельные «всплески», «пики» с анализом их причин, что важно для планирования работы врача, подразделения, службы.

1. простыми, состоящими из абсолютных величин;
2. сложными, состоящими из относительных или средних величин;
3. моментными, состоящими из величин, характеризующих размер явления на определенные даты, моменты (например, число случаев заболеваний дифтерией по годам), уровни моментного ряда не подлежат дроблению;
4. интервальными, состоящими из величин, характеризующих какие-либо итоги за определенный интервал времени (например, заболеваемость по годам, можно разделить поквартально, помесячно и т.д.), то есть данный ряд в отличие от моментного логически можно разделить на более дробные периоды.

1. укрупнение интервала путем суммирования уровней ряда за смежные периоды;
2. вычисление групповой средней (суммируются смежные уровни соседних периодов, а затем полученную сумму делят на число слагаемых);
3. вычисление скользящей средней (позволяет каждый уровень заменить на среднюю величину данного уровня и двух соседних с ними);
4. метод наименьших квадратов.

Метод наименьших квадратов

Динамика развития лучше всего может быть выражена линией, которая наиболее близко подходит к фактическим данным. Это достигается методом наименьших квадратов, который наиболее объективно выявляет тенденцию развития изучаемого явления.

Сначала определяется характер изменения изучаемого явления. В зависимости от характера кривой определяют характер уравнения зависимости между явлением и временем.

Имеется много различных уравнений, выражающих зависимость между двумя изучаемыми явлениями. Например, если тенденция прямолинейная, то она представляется в виде прямой линии, уравнение которой y = a + bx (парабола I порядка). Если тенденция криволинейная, то она может быть представлена в виде параболы II порядка (уравнение y = a + bx +cx 2 ), параболой III порядка (y = a + bx +cx 2 + dx 3 ) или параболой n-го порядка.

Чаще всего в практике здравоохранения используется выравнивание по параболе I и II порядка.

Проведем выравнивание показателей младенческой смертности, имеющих прямолинейную тенденцию развития, по способу наименьших квадратов, используя параболу I порядка (табл. 2).

Для определения точности выравнивания (аппроксимации) используют формулу: 5%

Источник: topuch.com