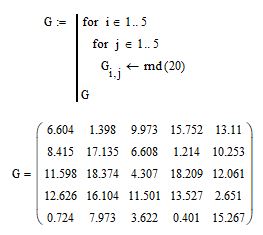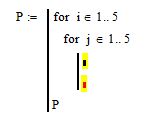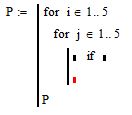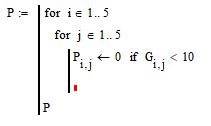Как работать в программе mathcad

Большинству студентов и преподавателей необходимы численные или аналитические расчеты, например, для численного решения уравнения или вычисления производной. Чтобы произвести подобного рода расчеты, обойтись калькулятором вам не удастся. Нужные расчеты можно выполнить, разработав специальную программу, но для этого требуются существенные знания и время.

Данные программы могут быть полезны и в дальнейшей профессиональной деятельно­сти студентов, например, для инженерных задач на производстве или планирования бизнеса.

Программы MATLAB и Mathcad будут описываться в разных частях главы, хотя примеры, как правило, будут совпадать, чтобы подчеркнуть различия этих программ. Основные математические понятия, например, неопределенный интеграл, будем предполагать из­вестными.

Основные принципы работы и возможности программ MATLAB и Mathcad

Программы MATLAB и Mathcad предназначены, в первую очередь, для проведения мате­матических и технических расчетов. Как уже упоминалось, расчеты бывают численными и аналитическими. Численные расчеты обеспечивают получение конкретных числовых результатов при решении задачи, например, уравнения. Аналитические вычисления по­зволяют решить задачу в символьном виде, т.е. представить результат в виде математи­ческих формул, например, найти неопределенный интеграл. Следует отметить, что большинство задач не имеют аналитических или символьных решений, а требуют чис­ленных расчетов.

Как работать с программой mathCad

Как правило, работа с программами MATLAB и Mathcad заключается во вводе данных, проведении необходимых вычислений и получении результатов. При выполнении чис­ленных расчетов можно решить систему линейных уравнений (см. опыты «Решение сис­темы линейных уравнений»), найти минимум функции (см. опыты «Поиск минимума функции»), решить нелинейное уравнение (см. опыты «Поиск корня нелинейного урав­нения»), вычислить определенный интеграл (см. опыты «Численное интегрирование»), решить дифференциальное уравнение (см. опыты «Решение дифференциальных уравне­ний»). Аналитические вычисления позволяют находить производную и неопределенный интеграл (см. опыты «Аналитическое вычисление производной и интеграла»), выпол­нять символьные операции с математическими выражениями (см. опыты «Символьные операции с математическими выражениями и матрицами»), аналитически решать ряд алгебраических и дифференциальных уравнений (см. опыты «Аналитическое решение уравнений»).

Особое место в программах MATLAB и Mathcad занимают средства визуализации, кото­рые существенно упрощают решение задачи и интерпретацию результатов вычислений. Вы можете представить исходные данные или решение задачи в виде графиков и диа­грамм (см. опыты «Построение графиков и диаграмм»), трехмерных поверхностей (см. опыты «Трехмерные поверхности»), использовать анимационную или, другими сло­вами, динамическую графику (см. опыты «Анимационная графика»).

Может оказаться, что для решения вашей задачи, например, требующей вычислений разных типов, программы MATLAB и Mathcad не содержат необходимые средства. Дан­ные программы обладают встроенными языками программирования, которые позволяют создавать новые функции, используя существующие инструменты для расчетов. Кроме того, вы можете разработать нужную функцию на других языках программирования, например, на языке С [Си], и подключить ее к нашим программам.

1. MathCad. Вычисление значений числовых выражений

В программе Mathcad входной язык приближен к естественному математическому язы­ку, например, для записи интеграла следует воспользоваться значком .Кроме того, данная программа содержит средства для красивого оформления текста, например, мож­но изменить размер символов или выровнять текст.

Входной язык программы MATLAB является полностью текстовым, например, для вы­числения интеграла нужно ввести текстовую функцию. Данная программа основана на работе с матрицами, о чем свидетельствует происхождение ее названия — MATrix LABo- ratory (Матричная лаборатория). Числа рассматриваются в программе как матрицы еди­ничного размера для единообразного выполнения операций и функций. Более подробно работа с матрицами будет рассмотрена в опыте «Операции с матрицами» части «Работа­ем с программой MATLAB».

Источник: mydocx.ru

Элементы программирования в MathCad 15

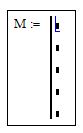
Для примера рассмотрим пример заполнения матрицы-вектора в автоматическом режиме. Предположим, что нам нужно заполнить матрицу случайными числами. Размер матрицы 10 элементов. Заполнение в ручную такой матрицы безусловно отнимет массу времени

В свободном поле mathcad введите имя вашей будущей матрицы M. Поставте знак присвоить «: ]». В место привычного маркера возникнет вертикальная черная черта с двумя маркерами. Удерживая клавишу Alt введите еще несколько раз символ «]» так, чтобы увеличить число свободных маркеров. Можно также воспользоваться кнопкой «Add Line» на панели Programming. В этих маркерах записываются строки кода

Рис. 1. Подготовка к написанию кода

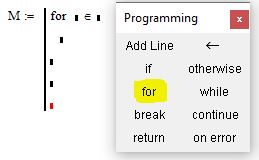
Поместите курсор в первый маркер и на панели Programming нажмите кнопку с надписью «for». Вы увидите заготовку для формирования цикла FOR с маркером для ввода «тела цикла», который несколько отстоит от основных маркеров

Рис. 2. Запись безусловного цикла FOR

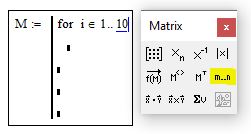
Теперь нужно ввести переменную-счетчик (пусть это будет «i»), которая будет менять свое значение от 1 до 10. Диапазон от 1 до 10 задается с помощью ранжированной переменной, которую можно найти на панели Matrix

Рис. 3. Настройка параметров цикла for в mathcad 15

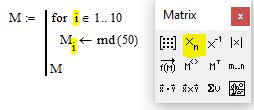
Цикл for в этом примере будет перебирать значения счетчика i от 1 до 10 c шагом 1. При каждом значении i элементу матрицы с соответсвующим индексом будет присваиваться случайное число с помощью стандартной функции rnd(m). Функция rnd присваивает переменной значение в диапазоне от 0 до «m»

Операция присваивания осуществляется при помощи операции Local difinition с панели Programming. Опрерация присваивания отображена в виде стрелочки «. Чтобы присвоить какое либо значение элементу матрицы нужно указать соответсвующий индекс матрицы. Это делается с помощью кнопки Subscript на панели Matrix.

Операция присваиваивания должна осуществляться в «теле цикла». То есть, все действия, которые должны повторяться по мере работы счетчика циклы, должны находиться в соответсвующих маркерах. После завершения работы цикла в последний маркер тела программы нужно ввести имя матрицы, над заполнением которой мы работали. В нашем случае это M. См. рисунок 4

Рис. 4. Синтаксис программы по заполнению матрицы-вектора случайными числами в mathcad 15

Теперь можно посмотреть на результат. Введем имя матрицы M и поставим знак равно » /static/images/mathcad/coding_5.JPG»>

Рис. 5. Результат работы программы в mathcad 15

Можно изменить программу таким образом, чтобы заполнить квадратную матрицу. Для этого нам нужно ввести еще один счетчик и еще один цикл for с индексом j. Таким образом один цикл будет выполняться внутри другого, формируя столбцы и строки матрицы

Рис. 6. Программа для заполнения квадратной матрицы в mathcad 15

Программы в mathcad могут использовать значения переменных, находящихся вне тела программы. Например, на рисунке ниже видно, как можно конечные значения счетчиков цикла связать со значениями переменных из вне

Рис. 7. Программа для заполнения квадратной матрицы в mathcad 15

Условные операторы «IF» в mathcad 15

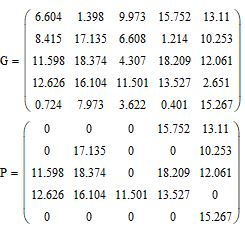
Чтобы посмотреть, как работает условный оператор «if» в mathcad 15 рассмотрим простой пример. Заполним квадратную матрицу G размером 5 х 5 элементов случайными числами и затем обнулим все элементы, которые меньше 10

На рисунке 8 приведен уже знакомый код заполнения матрицы случайными числами

Рис. 8. Программа для заполнения квадратной матрицы случайными числами

Для обнуления элементов, значение которых меньше 10, запишем второй участок кода с использованием условного оператора «If». Для проверки каждого элемента на выполнение этого условия нам опять потребуется два вложенных цикла «for» с счетчиками i и j. См. рис. 9. Обратите внимание, в теле второго цикла оставлено два свободных маркера

Рис. 9. Заготовка для применения условного оператора

Результат работы программы для удобства будет записываться в матрицу P. Поместите курсор в первый свободный маркер и нажмите на кнопку с надписью «if» на панели Programming. Вы увидите заготовку для записи условного оператора

Рис. 10. Заготовка для условного оператора

В этой заготовке выполним обнуление элемента матрицы G если значение этого элемента менее 10. Присвоение элементу матрицы значение нуля осуществляется символом » . Буквально логика данной операции следующая: «присвоить элементу матрицы P с текущим индексом i и j значение 0 если елемент матрицы G с тем же индексом меньше 10»

Рис. 11. Ввод условного оператора в mathcad 15

Теперь запишем второе условие, по которому все элементы матрицы G, которые больше либо равны 10 попадают в матрицу P без изменеий на те же «мееста». Буквально логика данной операции следующая: «присвоить элементу матрицы P с текущим индексом i и j значение елемента матрицы G с тем же индексом если значение элемента больше либо равно 10». Сразу же после текста программы можно вывести результат. См. рис. 12.

Рис. 12. Ввод условного оператора в mathcad 15

Теперь можно наглядно увидеть, как изменилась матрица после ее обработки условными операторами

Рис. 13. Результат работы условного оператора

Цикл «WHILE» в mathcad 15

Цикл While является условным циклом. То есть повторение его тела осуществляется до тех пор пока верно условие.

Рис. 14. Цикл WHILE в mathcad

В теле цикла могут находиться абсолютно любые команды и операторы: арифметические вычисления, открытие, анализ, обработка и запись данных в файл, запуск скриптов и приложений и т.д. Одним словом программирование это очень полезный и весьма универсальный инструмент, который позволяет реализовать любую идею в инженерной деятельности

Обратите внимание на то, что если в процессе выполнения программы условие запуска цикла «while» всегда оказывается верным, то цикл не завершится. Произойдет так называемое «зацикливание» программы и придется прерывать процесс счета вручную и искать ошибку

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit.

Pellentesque enim turpis, hendrerit tristique.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas.

In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.

Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.

Форма обратной связи

Поделиться

Статистика

Источник: student-engineer.pro

Приемы работы с системой MathCad

Документ программы MathCad называется рабочим листом. Он содержит объекты:

формулы и текстовые блоки. Ввод информации осуществляется в месте расположения курсора.

Программа MathCad использует три вида курсоров. Если ни один объект не выбран, используется крестообразный курсор, определяющий место создания следующего объекта. При вводе формул используется уголковый курсор, указывающий текущий элемент выражения. При вводе данных в текстовый блок применяется текстовый курсор в виде вертикальной черты (см.рис. 3.1)

Рисунок 3.1 — Курсор и местозаполнители, относящиеся к редактированию формул

Формулы — основные объекты рабочего листа. Новый объект по умолчанию является формулой. Чтобы начать ввод формулы, надо установить крестообразный курсор в нужное место и начать ввод букв, цифр, знаков операций. При этом создается область формулы, в которой появляется уголковый курсор, охватывающий текущий элемент формулы, например имя переменной (функции) или число.

При вводе бинарного оператора по другую сторону знака операции автоматически появляется заполнитель в виде черного прямоугольника. В это место вводят очередной операнд. Для управления порядком операций используют скобки, которые можно вводить вручную. Уголковый курсор позволяет автоматизировать такие действия.

Чтобы выделить элементы формулы, которые в рамках операции должны рассматриваться как единое целое, используют клавишу ПРОБЕЛ. При каждом ее нажатии уголковый курсор «расширяется», охватывая элементы формулы, примыкающие к данному. После ввода знака операции элементы в пределах уголкового курсора автоматически заключаются в скобки (см.рис.3.2). Элементы формул можно вводить с клавиатуры или с помощью специальных панелей управления. Панели управления открывают с помощью меню View (Вид) или кнопками панели управления Math (Математика). Для ввода элементов формул предназначены следующие панели:

. панель управления Arithmetic (Счет) для ввода чисел, знаков типичных математических операций и наиболее часто употребляемых стандартных функций;

. панель управления Evaluation (Вычисление) для ввода операторов вычисления и знаков логических операций;

. панель управления Graph (График) для построения графиков;

. панель управления Matrix (Матрица) для ввода векторов и матриц и задания матричных операций;

. панель управления Calculus (Исчисление) для задания операций, относящихся к математическому анализу;

. панель управления Greek (Греческий алфавит) для ввода греческих букв (их можно также вводить с клавиатуры, если сразу после ввода соответствующего латинского символа нажимать сочетание клавиш CTRL+G, например [a][CTRL+G] — (, [W][CTRL+G]-();

. панель управления Symbolic (Аналитические вычисления) для управления аналитическими преобразованиями.

Рисунок 3.2 — Пример ввода формулы

Введенное выражение обычно вычисляют или присваивают переменной. Для вывода результата выражения используют знак вычисления, который выглядит как знак равенства и вводится при помощи кнопки Evaluate Expression (Вычислить выражение) на панели инструментов Evaluation (Вычисление).

Знак присваивания изображается как «:=», а вводится при помощи кнопки Assign Value (Присвоить значение) на панели инструментов Evaluation (Вычисление). Слева от знака присваивания указывают имя переменной. Переменную, которой присвоено значение, можно использовать далее в документе в вычисляемых выражениях. Чтобы узнать значение переменной, следует использовать оператор вычисления (см.рис. 3.3).

Рисунок 3.3 — Вставка оператора вывода

Текст, помещенный в рабочий лист, содержит комментарии и описания и предназначен для ознакомления, а не для использования в расчетах. Программа MathCad определяет назначение текущего блока автоматически при первом нажатии клавиши ПРОБЕЛ. Если введенный текст не может быть интерпретирован как формула, блок преобразуется в текстовый и последующие данные рассматриваются как текст (см.рис.3.4). Создать текстовый блок без использования автоматических средств позволяет команда Insert > Text Region (Вставка >Текстовый блок).

Рисунок 3.4 — Текстовые области (нижняя — в процессе редактирования)

Для форматирования формул и текста в программе MathCad используется панель инструментов Formatting (Форматирование). С ее помощью можно индивидуально отформатировать любую формулу или текстовый блок, задав гарнитуру и размер шрифта, а также полужирное, курсивное или подчеркнутое начертание символов.

В текстовых блоках можно также задавать тип выравнивания и применять маркированные и нумерованные списки.

Векторы и матрицы рассматриваются в программе MathCad как одномерные и двумерные массивы данных. Число строк и столбцов матрицы задается в диалоговом окне Insert Matrix (Вставка матрицы), которое открывают командой Insert > Matrix (Вставка > Матрица). Вектор задается как матрица, имеющая один столбец.

Для матриц определены следующие операции: сложение, умножение на число, перемножение и прочие (см.рис.3.5).

Рисунок 3.5 — Сложение и вычитание матриц

Допустимо использование матриц вместо скалярных выражений: в этом случае предполагается, что указанные действия должны быть применены к каждому элементу матрицы, и результат также представляется в виде матрицы.

Для работы с элементами матрицы используют индексы элементов. Нумерация строк и столбцов матрицы начинается с нуля. Индекс элемента задается числом, переменной или выражением и отображается как нижний индекс. Он вводится после щелчка на кнопке Subscript (Индекс) на панели инструментов Matrix (Матрица). Пара индексов, определяющих элемент матрицы, разделяется запятой.

Чтобы задать общую формулу элементов матрицы, типа МI,J:= i +j, используют диапазоны. Диапазон фактически представляет собой вектор, содержащий арифметическую прогрессию, определенную первым, вторым и последним элементами. Чтобы задать диапазон, следует указать значение первого элемента, через запятую значение второго и через точку с запятой значение последнего элемента. Точка с запятой при задании диапазона отображается как две точки (..). Диапазон можно использовать как значение переменной, например x:= 0,0.01.. 1.

Произвольные зависимости между входными и выходными параметрами задаются при помощи функций. Функции принимают набор параметров и возвращают значение, скалярное или векторное (матричное). В формулах можно использовать стандартные встроенные функции, а также функции, определенные пользователем (см.рис.3.6).

Рисунок 3.6 — Определение функции пользователем

Чтобы использовать функцию в выражении, надо определить значения входных параметров в скобках после имени функции. Имена простейших математических функций можно ввести с панели инструментов Arithmetic (Счет). Информацию о других функциях можно почерпнуть в справочной системе. Вставить в выражение стандартную функцию можно при помощи команды Insert > Function (Вставка >Функция).

В диалоговом окне Insert Function (Вставка функции) слева выбирается категория, к которой относится функция, а справа — конкретная функция. В нижней части окна выдается информация о выбранной функции. При вводе функции через это диалоговое окно автоматически добавляются скобки и заполнители для значений параметров. Пользовательские функции должны быть сначала определены.

Определение задается при помощи оператора присваивания. В левой части указывается имя пользовательской функции и, в скобках, формальные параметры — переменные, от которых она зависит. Справа от знака присваивания эти переменные должны использоваться в выражении. При использовании пользовательской функции в последующих формулах ее имя вводят вручную. В диалоговом окне Insert Function (Вставка функции) оно не отображается.

Для численного поиска корней уравнения в программе MathCad используется функция root. Она служит для решения уравнений вида f(x) = 0, где f (х) — выражение, корни которого нужно найти, a x — неизвестное. Для поиска корней с помощью функции root, надо присвоить искомой переменной начальное значение, а затем вычислить корень при помощи вызова функции: root(f(x),x) (см.рис.3.7). Здесь f(x) — функция переменной х, используемой в качестве второго параметра. Функция root возвращает значение независимой переменной, обращающее функцию f(x) в 0.

Рисунок 3.7 — Поиск корня нелинейного алгебраического уравнения

Если уравнение имеет несколько корней, то результат, выдаваемый функцией root, зависит от выбранного начального приближения.

Если функция f (х) является полиномом, то все его корни можно определить, используя встроенную функцию polyroots(v), где v — вектор, составленный из коэффициентов полинома (см.рис.3.8).

Рисунок 3.8 — Поиск корня полинома

Если надо решить систему уравнений (неравенств), используют так называемый блок решения, который начинается с ключевого слова given (дано) и заканчивается вызовом функции find (найти). Между ними располагают «логические утверждения», задающие ограничения на значения искомых величин, иными словами, уравнения и неравенства. Всем переменным, используемым для обозначения неизвестных величин, должны быть заранее присвоены начальные значения (см.рис.3.9).

Рисунок 3.9 — Решение системы уравнений

Чтобы записать уравнение, в котором утверждается, что левая и правая части равны, используется знак логического равенства — кнопка Boolean Equals (Логически равно) на панели инструментов Evaluation (Вычисление). Другие знаки логических условий также можно найти на этой панели. Заканчивается блок решения вызовом функции find, у которой в качестве аргументов должны быть перечислены искомые величины. Эта функция возвращает вектор, содержащий вычисленные значения неизвестных (см.рис.3.10).

Рисунок 3.10 — Решение системы уравнений и неравенств

Чтобы построить двумерный график в координатных осях Х-У, надо дать команду Insert> Graph > X-Y Plot (Вставка > График > Декартовы координаты). В области размещения графика находятся заполнители для указания отображаемых выражений и диапазона изменения величин. В одной графической области можно построить несколько графиков.

Для этого надо у соответствующей оси перечислить несколько выражений через запятую. Разные кривые изображаются разным цветом, а для форматирования графика надо дважды щелкнуть на области графика. Для построения простейшего трехмерного графика, необходимо задать матрицу значений. Отобразить эту матрицу можно в виде поверхности — Insert > Graph > Surface Plot (Вставка > График > Поверхность), столбчатой диаграммы — Insert > Graph > 3D Bar Plot (Вставка > График > Столбчатая диаграмма) или линий уровня — Insert > Graph > Contour Plot (Вставка > График > Линии уровня).

С помощью аналитических вычислений находят аналитические или полные решения уравнений и систем, а также проводят преобразования сложных выражений (например, упрощение). Иначе говоря, при таком подходе можно получить нечисловой результат.

В программе MathCad конкретные значения, присвоенные переменным, при этом игнорируются — переменные рассматриваются как неопределенные параметры. Команды для выполнения аналитических вычислений в основном сосредоточены в меню Symbolics (Аналитические вычисления). Чтобы упростить выражение (или часть выражения), надо выбрать его при помощи уголкового курсора и дать команду Symbolics > Simplify (Аналитические вычисления > Упростить). При этом выполняются арифметические действия, сокращаются общие множители и приводятся подобные члены, применяются тригонометрические тождества, упрощаются выражения с радикалами, а также выражения, содержащие прямую и обратную функции (типа eInx). Некоторые действия по раскрытию скобок и упрощению сложных тригонометрических выражений требуют применения команды Symbolics > Expand (Аналитические вычисления > Раскрыть). Команду Symbolics > Simplify (Аналитические вычисления > Упростить) применяют и в более сложных случаях (см.рис.3.11)Например, с ее помощью можно:

. вычислить предел числовой последовательности, заданной общим членом;

. найти общую формулу для суммы членов числовой последовательности,

заданной общим членом;

. вычислить производную данной функции;

. найти первообразную данной функции или значение определенного

Рисунок 3.11 — Панель Symbolic

Наиболее заметная «изюминка» MathCAD, которую сразу оценили пользователи, — это встроенный язык программирования. В MathCAD, по сути, не встроен язык программирования, а просто снято ограничение на использование составных операторов в теле алгоритмических управляющих конструкций выбор и повторение. Кроме того, добавлены цикл с параметром и оператор досрочного выхода break. Алгоритмические конструкции и составные операторы в среде MathCAD вводятся нажимом одной из семи кнопок панели управления:

Add line — добавить строку программы, тела цикла, плеча альтернативы и т.д. ( — знак присвоения.

While — при нажатии на эту кнопку на экране появляется заготовка цикла с предпроверкой: слово while с двумя пустыми квадратиками. В квадратик правее while нужно записать булево выражение (переменную), управляющее циклом, а во второй квадратик (ниже while ) — тело цикла.

If — позволяет вводить в программу альтернативу с одним плечом.

Otherwise — позволяет превратить неполную альтернативу в полную:

for — кнопка для ввода в программы цикла с параметром.

Break — кнопка досрочного выхода из программы или цикла (см.рис.3.12)

Рисунок 3.12 — Панель инструментов Programming

Ещё одна важная возможность MathCAD — построение графиков. Чтобы построить двумерный график в координатных осях Х-У, надо дать команду Insert> Graph > X-Y Plot (Вставка > График > Декартовы координаты). В области размещения графика находятся заполнители для указания отображаемых выражений и диапазона изменения величин.

Заполнитель у середины оси координат предназначен для переменной или выражения, отображаемого по этой оси. Обычно используют диапазон или вектор значений. Граничные значения по осям выбираются автоматически в соответствии с диапазоном изменении величины, но их можно задать и вручную (см.рис.3.13). В одной графической области можно построить несколько графиков.

Для этого надо у соответствующей оси перечислить несколько выражений через запятую. Разные кривые изображаются разным цветом, а для форматирования графика надо дважды щелкнуть на области графика. Для управления отображением построенных линий служит вкладка Traces (Линии) в открывшемся диалоговом окне.

Текущий формат каждой линии приведен в списке, а под списком расположены элементы управления, позволяющие изменять формат. Поле Legend Label (Описание) задает описание линии, которое отображается только при сбросе флажка HideLegend (Скрыть описание). Список Symbol (Символ) позволяет выбрать маркеры для отдельных точек, список Line (Тип линии) задает тип линии, список Color (Цвет) — цвет.

Список Type (Тип) определяет способ связи отдельных точек, а список Width (Толщина) — толщину линии. Точно так же можно построить и отформатировать график в полярных координатах (см.нрис.3.14). Для его построения надо дать команду Insert > Graph > Polar Plot (Вставка > График> Полярные координаты).

Для построения простейшего трехмерного графика, необходимо задать матрицу значений. Отобразить эту матрицу можно в виде поверхности — Insert > Graph > Surface Plot (Вставка > График > Поверхность), столбчатой диаграммы — Insert > Graph > 3D Bar Plot (Вставка > График > Столбчатая диаграмма) или линий уровня — Insert > Graph >Contour Plot (Вставка > График > Линии уровня). Для отображения векторного поля при помощи команды Insert > Graph >Vector Field Plot (Вставка > График > Поле векторов) значения матрицы должны быть комплексными. В этом случае в каждой точке графика отображается вектор с координатами, равными действительной и мнимой частям элемента матрицы. Во всех этих случаях после создания области графика необходимо указать вместо заполнителя имя матрицы, содержащей необходимые значения.

программа формула матрица

Рисунок 3.13 — XY-график двух векторов

Рисунок 3.14 — Полярные графики

Для построения параметрического точечного графика командой Insert > Graph > 3D Scatter Plot (Вставка > График > Точки в пространстве) необходимо задать три вектора с одинаковым числом элементов, которые соответствуют х-, у- и z-координатам точек, отображаемых на графике(см.рис.3.15). В области графика эти три вектора указываются внутри скобок через запятую.

Аналогичным образом можно построить поверхность, заданную параметрически (см.рис.3.16). Для этого надо задать три матрицы, содержащие, соответственно, х-, у- и z-координаты точек поверхности. Теперь надо дать команду построения поверхности Insert > Graph >Surface Rot (Вставка > График > Поверхность) и указать в области графика эти три матрицы в скобках и через запятую. Таким образом можно построить практически любую криволинейную поверхность, в том числе с самопересечениями.

Рисунок 3.15 — 3D Scatter Plot — график множества точек

Рисунок 3.16 — График поверхности функции

Источник: vuzlit.com