Как работать в программе geogebra

Презентация на тему: » Краткое руководство для начинающих изучать программу GeoGebra M E T S.» — Транскрипт:

1 Краткое руководство для начинающих изучать программу GeoGebra M E T S

2 Company Logo GeoGebra свободно-распространяемая динамическая геометрическая среда, которая даёт возможность создавать «живые чертежи» в планиметрии, в частности, для построений с помощью циркуля и линейки. Кроме того, у программы богатые возможности работы с функциями (построение графиков, вычисление корней, экстремумов,интегралов и т.д.) за счёт команд встроенного языка (который, кстати, позволяет управлять и геометрическими построениями) Программа написана Маркусом Хохенвартером на языке Java (соответственно работает медленно, но на большом числе операционных систем). Переведена на 39 (по новым данным 45) языков. Полностью поддерживает русский язык. В настоящее время активно разрабатывается. Источник:

5 после установки программы изменяем язык на русский

6 Company Logo строка меню панель инструментов графическое окно кнопка сброса чертежа панель объектов или алгебраическое окно строка ввода

Геогебра. Урок первый. Как начать работать в Геогебре

7 Company Logo панель анимации кнопка отмены подсказка на панели инструментов кнопка повтора

8 Company Logo активная клавиша на панели инструментов красный треугольник в нижнем правом углу клавиши активизирует всплывающее окно

9 Company Logo всплывающее окно графического поля со свойствами выбранного объекта

10 Company Logo всплывающее окно панели объектов со свойствами выбранного объекта

11 Company Logo свойства выбранного объекта объект

12 Company Logo экспорт статичного чертежа в буфер обмена экспорт изображения В результате этих действий экспортируется только графическое поле

13 Company Logo чертёж скопирован в документ программы Word

14 Company Logo результат экспорта изображения

15 Company Logo пример: графики функций построены с использованием строки ввода

16 Company Logo чертёж экспортирован в документ программы Word, добавлены комментарии

17 Company Logo чертёж экспортирован в программу Notebook 10

18 Company Logo создание ползунка для динамического апплета активное окно подсказка всплывающее окно

19 Company Logo после создания ползунка, обязательно проверьте его в действии

20 Company Logo такой апплет требует коррекции

21 Company Logo привязка текста к объекту

22 Company Logo повторная проверка

23 Company Logo введение динамического текста

24 Company Logo статическая часть текста +динамическая часть текста+

25 Company Logo экспорт интерактивного чертежа при создании интеракивного чертежа экспортируются все панели и строки

26 Company Logo прежде, чем экспортировать интерактивный чертёж, уберите ненужные панели и строки

27 Company Logo затем сохраните файл с расширением *.ggb

28 Company Logo затем сохраните файл с расширением *.html самостоятельно определите, какую роль играет каждая из дополнительных функций

29 Company Logo совет: перед загрузкой интерактивного чертежа создайте отдельную папку для апплетов программы GeoGebra при экспорте интерактивного чертежа создаются файлы *.ggb, *.html и *.jar, которые должны быть всегда вместе

30 Company Logo о загрузке апплетов в Интернет читайте в справке

31 Company Logo Полезные ссылки Introduction to GeoGebra EUROPEAN VIRTUAL LABORATORY OF MATHEMATICS teacherbook.htm teacherbook.htm LFS’s Library ra%20Lessons ra%20Lessons Dave Matthews’ GeoGebra Pages

32 Company Logo Полезные ссылки Matemaatika on mõnus GeoGebrast ja dünaamilistest slaididest Dünaamilised slaidid matemaatika visualiseerimiseks _slaidid/CD/Tiitelleht.htm _slaidid/CD/Tiitelleht.htm Signum. Cообщения с ярлыком GeoGebra. Копилка. Загрузка апплетов в Интернет.

33 Company Logo Удачи в изучении программы! Автор презентации учитель математики Таллиннской Ляэнемере Гимназии Метс М.А.

Источник: www.myshared.ru

Использование СПО GeoGebra
статья по математике (5, 6, 7, 8, 9, 10, 11 класс)

GeoGebra – свободно распространяемая (GPL) динамическая геометрическая среда, которая даёт возможность создавать чертежи в планиметрии, в частности, для построений с помощью циркуля и линейки.

Кроме того, у программы богатые возможности работы с функциями (построение графиков, вычисление корней, экстремумов, интегралов и т.д.) за счёт команд встроенного языка (который, кстати, позволяет управлять и геометрическими построениями). Надо сказать, что она не просто известна в Интернете, а набирает популярность с каждым днем, в том числе, среди учителей математики средней школы.

Скачать:

Предварительный просмотр:

«ИСПОЛЬЗОВАНИЕ СПО GEOGEBRA»

GeoGebra – свободно распространяемая (GPL) динамическая геометрическая среда, которая даёт возможность создавать чертежи в планиметрии, в частности, для построений с помощью циркуля и линейки.

Кроме того, у программы богатые возможности работы с функциями (построение графиков, вычисление корней, экстремумов, интегралов и т.д.) за счёт команд встроенного языка (который, кстати, позволяет управлять и геометрическими построениями). Надо сказать, что она не просто известна в Интернете, а набирает популярность с каждым днем, в том числе, среди учителей математики средней школы.

GeoGebra поможет учителям для объяснения, а школьникам в ознакомлении с учебными материалами не только курса геометрии, но и алгебры, и математического анализа, будет незаменима в практиковании навыков и наглядном представлении. Очень просто с помощью этой программы построить точки, векторы, сегменты, линии и т.п., так же как функции, которые могут быть изменены динамически мышью впоследствии. С другой стороны возможен также прямой ввод в шкале-обозначений: g: 3x + 4y = 7 или c: (x – 2), 2 + (y – 3) 2 = 25 и целый ряд команд, включая дифференцирование и интеграцию. Самая замечательная особенность из GeoGebra – двойное представление объектов: каждое выражение в окне алгебры соответствует объекту в окне геометрии и наоборот.

• Построение кривых:
• Построение графиков функций y = f (x).
• Построение кривых, заданных параметрически в декартовой системе координат: x = f(t); y = g(t).
• Построение конических сечений.
• Построение геометрического места точек, зависящих от положения некоторой другой точки, принадлежащей какой-либо кривой или многоугольнику (инструмент Локус).

• Действия с матрицами.
• Вычисления с комплексными числами.
• Нахождение точек пересечения кривых.

Графика, алгебра и таблицы связаны между собой и полностью динамичны.

Легкий в использовании интерфейс, вдобавок обладает очень мощными возможностями. Можно сами создать интерактивный обучающий материал, такие как веб-страницы.

Доступна на многих языках есть русский вариант.

Одним из эффективных приёмов поиска решения уравнений, неравенств и их систем является приём геометрических интерпретаций. Однако в практике обучения алгебре и началам математического анализа он имеет ограниченное применение, связанное с большими затратами учебного времени и технической сложностью построения геометрических интерпретаций алгебраических объектов. Решение этой проблемы в использовании возможностей интерактивной геометрической среды GeoGebra, так как идейную основу ее создания составляет визуализация связей алгебры и геометрии (geometry +algebra).

К возможностям этой программы относится создание различных типов геометрических интерпретаций, которые позволяют использовать в процессе решения алгебраических задач такие методы, как функционально-графический, геометрический и метод геометрического места точек.

2. Применение GeoGebra на уроках математики

Для реализации функционально-графического метода необходимо, как известно, перевести условие алгебраической задачи в термины взаимного расположения графиков элементарных функций. При построении «вручную» желательно выбирать функции так, чтобы общий вид их графиков и свойств были хорошо известными. Использование GeoGebra позволяет не тратить время на подбор функций и исследование их свойств, так как для построения графика функции достаточно вести формулу, её задающую, в строку ввода.

Проиллюстрирую эти возможности GeoGebra конкретными примерами.

Решение. Введем в рассмотрение функции

Используя строку ввода, построим графики функций в GeoGebra. Отмечаем с помощью инструмента «Пересечение двух объектов» точку пересечения графиков. Выведем на экран имя и значение точки, используя вкладку «Свойства». Абсцисса является приближенным значением корня уравнения с выбранной точностью (рис. 1).

Рис. 1. Геометрическая интерпретация для решения задачи примера 1 функционально-графическим методом, выполненная в GeoGebra.

К помощи метода геометрических мест точек прибегают при решении алгебраических задач, сводящихся к системам (совокупностям) уравнений и неравенств с параметрами или двумя переменными. Применение этого метода вручную требует наличия у учащихся обширных знаний об уравнениях и неравенствах, задающих опорные геометрические места точек, хорошей логической и теоретико-множественной подготовки учащихся, включающей умения находить пересечение или объединения множеств, построенных на координатной плоскости, в соответствии со смыслом логических операций. Использование GeoGebra не требует владения этими знаниями и умениями. Данная среда позволяет получать геометрическую интерпретацию после записи в строке ввода совокупностей (систем) уравнений и неравенств с помощью логических связок.

Решение задачи примера 1 геометрическим методом. Подкоренные выражения слагаемых в левой части уравнения сходны по структуре с теоремой косинусов для треугольников: 1) со сторонами 5, x и углом между ними 45°; 2) со сторонами 12, x и углом 45°. Тогда, интерпретируя уравнение на языке этих геометрических фигур, получаем, что сумма сторон, лежащих против углов в 45°, равна 13.

С помощью инструмента «Ползунок» в GeoGebra введем параметр x, это позволит получить динамический чертеж, состоящий из описанных выше треугольников (рис. 3а, б). Для получения ответа достаточно, меняя положение ползунка, подобрать такое значение x, при котором сумма длин интересующих нас сторон равна 13. Заметим, что при несвязном построении треугольников (рис. 3б) компьютерное решение не помогает обнаружить аналитическое.

Рис. 3. Геометрическая интерпретация для решения задачи примера 1 геометрическим методом, выполненная в GeoGebra.

Введя в строку ввода ((x^2+y^2≤4) ∧ (y>abs(x))) ∨ ((x^2+y^2≥4) ∧ (y

Рис. 2. Геометрическая интерпретация для решения задачи примера 2 методом геометрических мест точек, выполненная в GeoGebra.

Для применения геометрического метода к решению алгебраических задач необходимо придать переменным и выражениям, зависящим от них, смысл геометрических величин. Затем построить фигуру, обладающую соответствующими метрическими свойствами. Полученная геометрическая интерпретация позволяет найти значение переменной с использованием знаний о позиционных и метрических свойствах фигуры и её элементов. Очевидным ограничением данного метода является нахождение лишь неотрицательных значений переменной. Построение геометрических фигур в GeoGebra позволяет «считывать» искомое значение с чертежа или находить его экспериментально, используя динамичность изображения.

Решения примеров 1 и 2 показывают, что возможности интерактивной геометрической среды хоть и велики, но не безграничны. Так, если результат решения задачи не может быть выражен целым числом или конечной десятичной дробью, то компьютерное решение не позволит нам получить точное значение результата. Кроме того, компьютерное решение задачи далеко не всегда согласуется и помогает обнаружить аналитическое решение. Заметим также, что большинство интерактивных геометрических сред имеют ограничения в использовании, связанные с непродуманностью во всех деталях алгоритмов их разработки. Так, GeoGebra 4.2 позволяет задавать через строку ввода не любые зависимости, распознает не все точки пересечения графических объектов, разделяет смысловые значения графических объектов при использовании инструмента «Исследователь функций», например не работает с графиками линейных и квадратичных функций, считая их геометрическими объектами (коническими сечениями).

ПРИМЕР 3 Фрагмент урока о доказательстве суммы углов треугольника.

Ребята, в каком треугольнике, по вашему мнению, сумма внутренних углов будет больше? (В тупоугольном)

Почему? (Градусная мера тупого угла больше острого или прямого, значит, и сумма будет больше.)

Практика показывает, что почти в каждом классе найдутся несколько человек, которые, зная, что тупой угол всегда больше острого, по аналогии скажут, что сумма внутренних углов тупоугольного треугольника больше.

Кто-то может возразить. В результате чего мнения разделятся.

Мнения разделились. Давайте проверим кто же прав. Древние греки на основе наблюдений и из практического опыта делали выводы, выдвигали предположения (гипотезы) о свойствах различных фигур, а затем эти гипотезы пытались обосновать и доказать. В то время и сложилось утверждение: «В споре рождается истина».

Давайте и мы проведем небольшое исследование с помощью интерактивной модели треугольника.

У вас на партах лежит таблица для исследования, в которую мы будем заносить результаты наших наблюдений. Точно такая же таблица на доске.

Источник: nsportal.ru

Знакомство с программой Geogebra

Данное методическое пособие (фрагмент тетради-коспекта) предназначено помочь учащимся при изучении курса математики и информатики. Предложенные задания позволяют эффективно построить работу по повторению пройденного материала, по введению новых понятий и определений, по закреплению материала, воплотить систему контроля знаний и навыков. Задания имеют практическую направленность, что соответствует требованиям ФГОС на подготовку учащихся к жизни в информационном обществе.

В тетради-конспекте кратко представлен теоретический материал по трем темам. Тема №1 «Основы использования программы GeoGebra», тема №2 «Прямоугольник. Построение прямоугольника», тема №3 «Треугольник. Построение равностороннего треугольника», что соответствует календарному планированию учебного материала по математике в 5-7-х классах. Предложено 6 заданий для выполнения в ходе рассмотрения теоретического материала, приведено несколько примеров решения поставленных задач с пошаговым выполнением алгоритма, 10 практических заданий для самостоятельного выполнения дома и 11 вопросов для самоконтроля, а также 3 практические работы на построения чертежа в динамической геометрической среде GeoGebra.

Тема №1 «Основы использования программы GeoGebra». В ходе изучения теоретического материала по данной теме, учитель предлагает учащимся выполнить 2 задания. 3 практических задания для самостоятельного выполнения, предназначенных для закрепления навыков работы в программе GeoGebra. Также эти задания можно предложить некоторым учащимся на уроке.

Вопросы для самопроверки предназначены для усвоения основных понятий по теме. Выполнив все эти задания, учащиеся смогут подготовиться к самостоятельной работе по данной теме и применить свои знания на уроках математики.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

Просмотр содержимого документа
«Знакомство с программой Geogebra »

Знакомство с программой GeoGebra.

Тетрадь-конспект включает не только материал по изучению интерактивной геометрической среды GeoGebra, но и теоретические сведения, задания по теоретической части, вопросы для самопроверки, упражнения для домашней работы, основные практические приемы построения. Содержательный аспект тетради-конспекта отличается связностью и систематичностью. В приложении №1 тетеради-конспекта приведен пример урока по теме: «Основы использования программы GeoGebra» (Приложение 1).

Тетрадь-конспект может быть рекомендована и учащимся 6-х, 7-х классов, т.к. позволит получить дополнительные знания, необходимые при выполнении самостоятельных или практических работ по математике, а так же учащимся 5-х классов в рамках занятий на уроках математики и информатики.

Тетрадь-конспект (фрагмент).

Тема №1. Основы использования программы GeoGebra.

Цель: познакомиться с интерфейсом и панелью инструментов программы.

Знакомство с динамической средой GeoGebra.

GeoGebra — бесплатная программа предоставляющая возможность создания динамических («живых») чертежей для использования на разных уровнях обучения геометрии, алгебры, планиметрии и других смежных дисциплин. Программа обладает богатыми возможностями работы с функциями.

В отличии от других программ для динамического манипулирования геометрическими объектами, идея GeoGebra заключается в интерактивном сочетании геометрического, алгебраического и числового представления. В данной программе можно создавать конструкции с точками, векторами, линиями, коническими сечениями, а также математическими функциями, а затем динамически изменять их. Кроме того, GeoGebra позволяет напрямую вводить уравнения и манипулировать координатами. Таким образом, можно легко составлять графики функций, работать со слайдерами для подбора необходимых параметров, искать символические производные, и использовать мощные команды вроде корня и последовательности.

Окно программы GeoGebra.

После запуска программы появляется окно (рис.1).

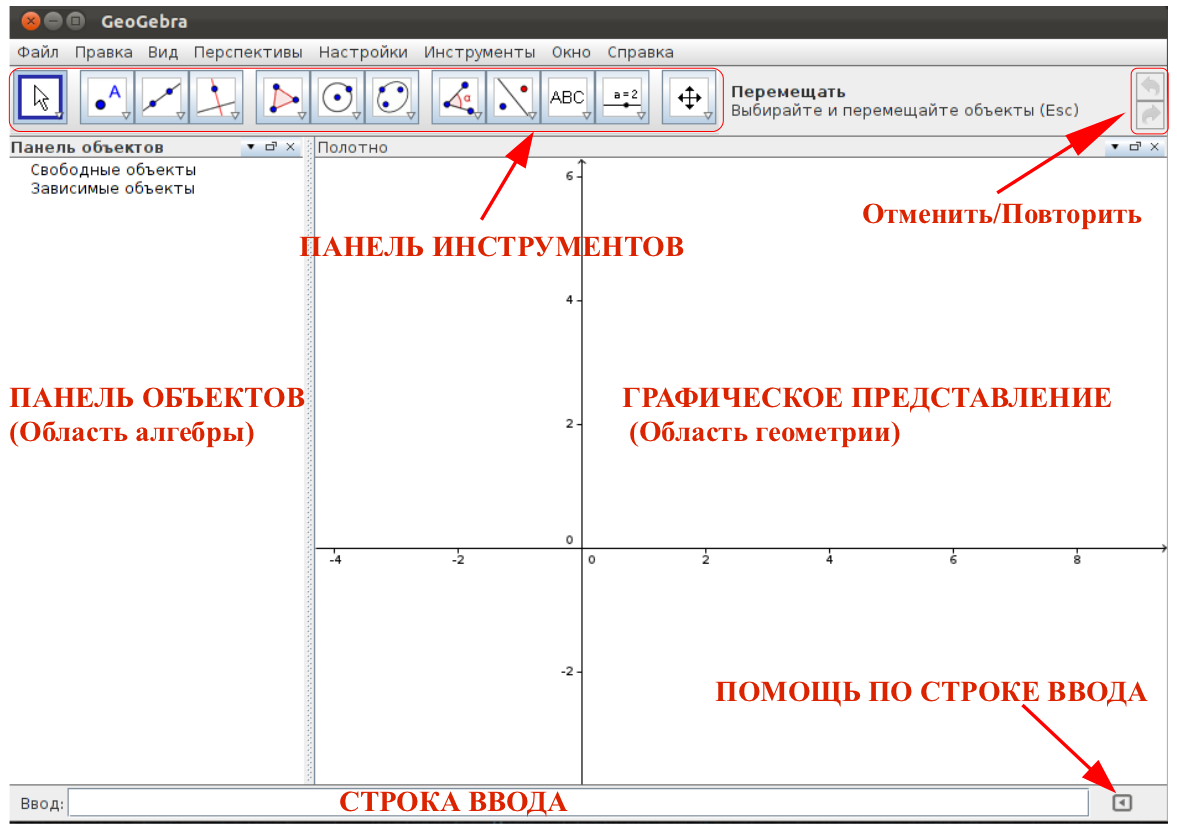
Рис.1. Окно программы GeoGebra.

С помощью инструментов на Панели инструментов можно строить различные чертежи, используя мышь. Одновременно с добавлением чертежа в Графическое представление соответствующие координаты появятся и на Панели объектов. Строка ввода служит для непосредственного ввода построений за счёт координат, уравнений, команд и функций. После нажатия на клавишу Enter, они сразу появятся в области графического представления и панели объектов.

1. Главное меню: основное меню окна, как и во многих приложениях выполняет все основные функции программы.

2. Панель инструментов: на этой панели расположены все основные инструменты, которые позволяют выполнять построения при помощи мыши. Достаточно выбрать интересующий объект и нажать на графическое представление.

3. Отменить/Повторить: две кнопки, верхняя позволяет отменить последние действия, нижняя повторить отменённое действие.

4. Графическое представление (Область геометрии): основная область, в которой будут выполняться все построения.

5. Панель объектов (Область алгебры): область в которой будут записаны все математические формулы построения.

6. Строка ввода: данная область позволяет вводить различные формулы, функции, уравнения, которые сразу отобразятся в панели объектов и на графическом представлении.

7. Помощь по строке ввода: позволяет просмотреть весь список команд для строки ввода.

За счёт инструментов в панели инструментов можно выполнять построения в графическом представлении (области геометрии) с помощью мыши. В то же самое время соответствующие координаты и уравнения будут показаны на панели объектов (области алгебры). Строка ввода используется для ввода координат, уравнений, команд и функций с клавиатуры; все эти объекты будут показаны в графическое представление и на панели объектов сразу после нажатия клавиши ENTER. В GeoGebra, геометрия и алгебра всегда вместе.

В начале средней школы, начать работать лучше с чистого листа на графическом виде полотна и с инструментами геометрии. В дальнейшем, можно будет ввести систему координат с использованием сетки для более удобной работы с целыми координатами. В средней школе, можно уже будет использовать алгебраический ввод данных.

Для быстрого доступа к некоторым возможностям заданной конфигурации пользовательского интерфейса, можно использовать возможности Боковой панели, нажав на панели справа от Графического Вида.

Задание 1. Установите соответствие между элементами окна (рис.2) и номерами, которыми они обозначены, в таблице 1.

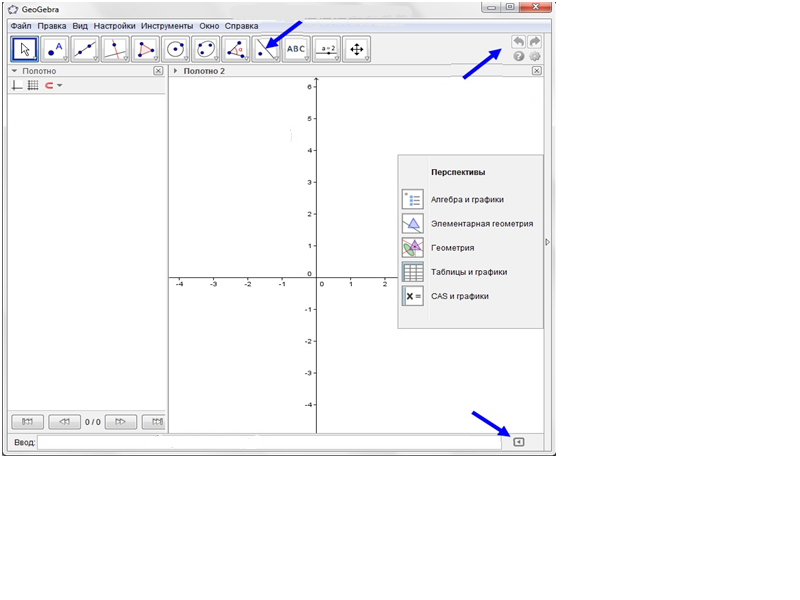
Рис. 2. Элементы окна GeoGebra.

Таблица1. Элементы окна GeoGebra.

Помощь по строке ввода

Элементы главного меню.

Главное меню – это специальная панель инструментов, расположенная в верхней части экрана, которая содержит такие групповые меню, как Файл, Правка, Вид и т. д.

При выборе меню отображается список команд, включенный в группу. Рядом с некоторыми командами отображаются соответствующие им значки и/или функциональные клавиши. Команды, недоступные для Текущего выбора, не высвечиваются.

Файл – содержит команды основных операций;

Правка – позволяет редактировать изображение;

Вид – содержит различные настройки рабочего окна, помогающие пользователю в работе;

Настройки – данное меню позволяет форматировать объекты;

Инструменты – позволяет создать новый инструмент или управлять существующим;

Окно – с помощью этого меню можно создать новое окно;

Справка – содержит команды справочной системы.

Панель инструментов.

Панель инструментов дублирует раздел «Инструменты» из главного меню. Эта панель необходима для более быстрого доступа к основным построениям в программе.

При помощи панели инструментов, большую часть вычислений и построений, можно провести при помощи мыши, что делает возможным использование программы GeoGebra вместе с интерактивной доской.

Далее рассмотрим каждый из элементов панели инструментов (рис.3) по группам, на которые они разделены (таблица 2).

Рис.3. Элементы панели инструментов.

Таблица 2. Элементы панели инструментов.

Описание элемента панели инструментов

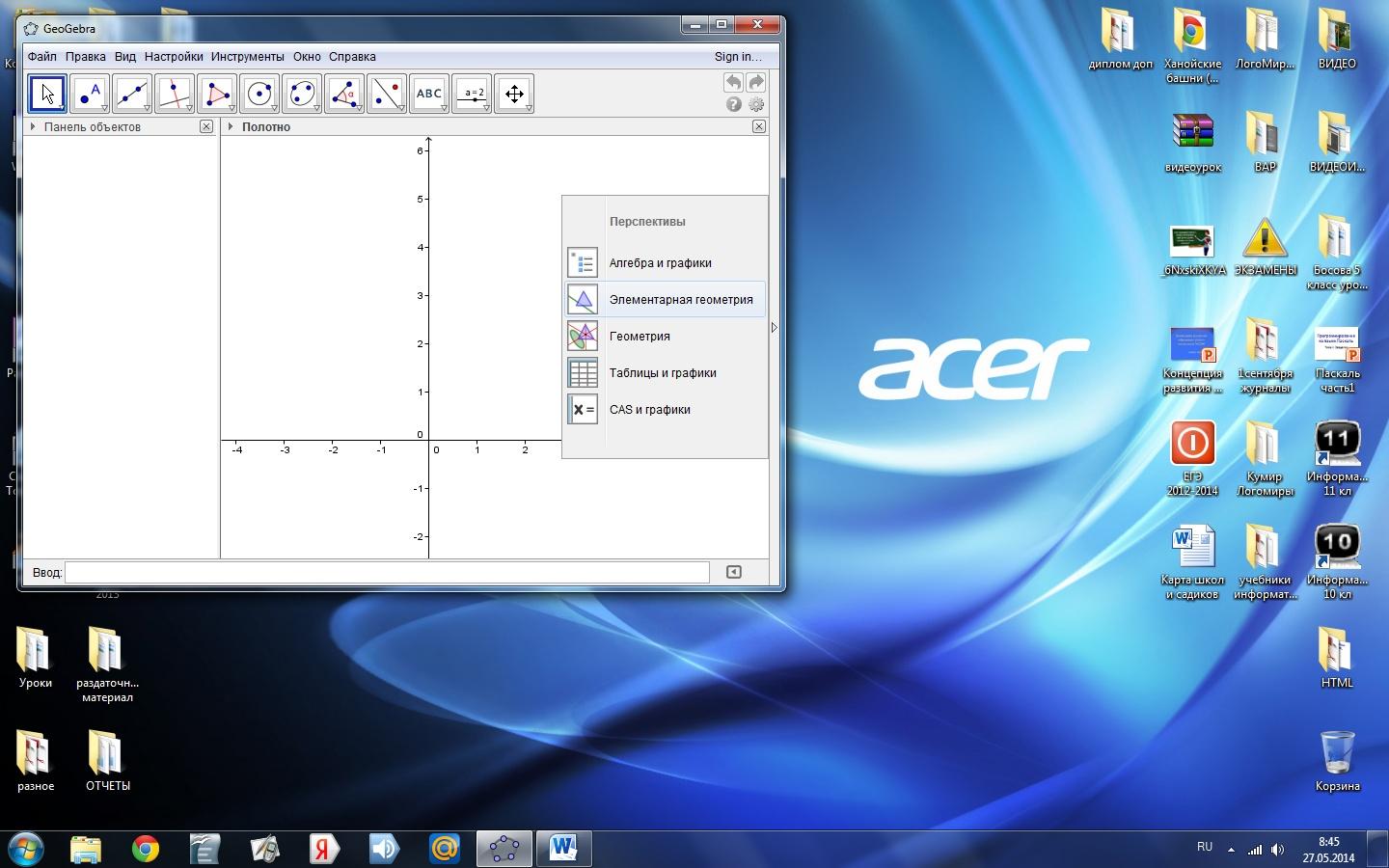
Перемещать (выбирайте и перемещайте объекты)

Точка (щелкните на полотне или линии)

Прямая (укажите две точки прямой)

Перпендикулярная прямая (укажите точку и перпендикулярную прямую)

Многоугольник (укажите по очереди все вершины многоугольника, а затем снова укажите первую из них)

Окружность по центру и точке (укажите центр окружности и точку на ней)

Эллипс (укажите фокусы эллипса и точку на нем)

Угол (выберите три точки или две прямые)

Отражение относительно прямой (укажите исходный объект и прямую отражения)

Текст (щелкните на полотне или в точке, чтобы создать надпись)

Ползунок (щелкните на чертеже, чтобы создать ползунок)

Переметить чертеж (перетащите чертеж или ось, с нажатой клавишей Shift)

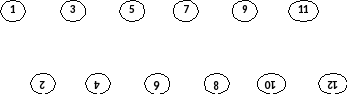
Задание 2. Определить кнопки панели инструментов (рис.4.) и написать их названия по образцу (Подсказка: если навести курсор мыши на инструмент, под ним появится его название).

Рис. 4. Кнопки панели инструментов

Практическая работа № 1. Тема: Создание чертежей. Цель: приобрести практические навыки работы с окном программы GeoGebra; создание изображения с помощью панели инструментов; сохранение файла. Инструктивная карта практического задания. Задание. Создайте свой первый рисунок в программе GeoGebra используя панель инструментов. В таблице 5 представлены основные элементы панели инструментов необходимые для выполнения данного задания. Таблица 5. Основные элементы панели инструментов для практической работы.

Изображение	Обозначение	Подсказка
	Перемещать (курсор)	Перетащите свободный объект с помощью мыши.
	Точка (новая точка)	Щелкните на Графический вид или на уже существующий объект, чтобы создать новую точку.
	Прямая (по двум точкам)	Щелкните на Графический вид два раза или на уже существующие две точки.
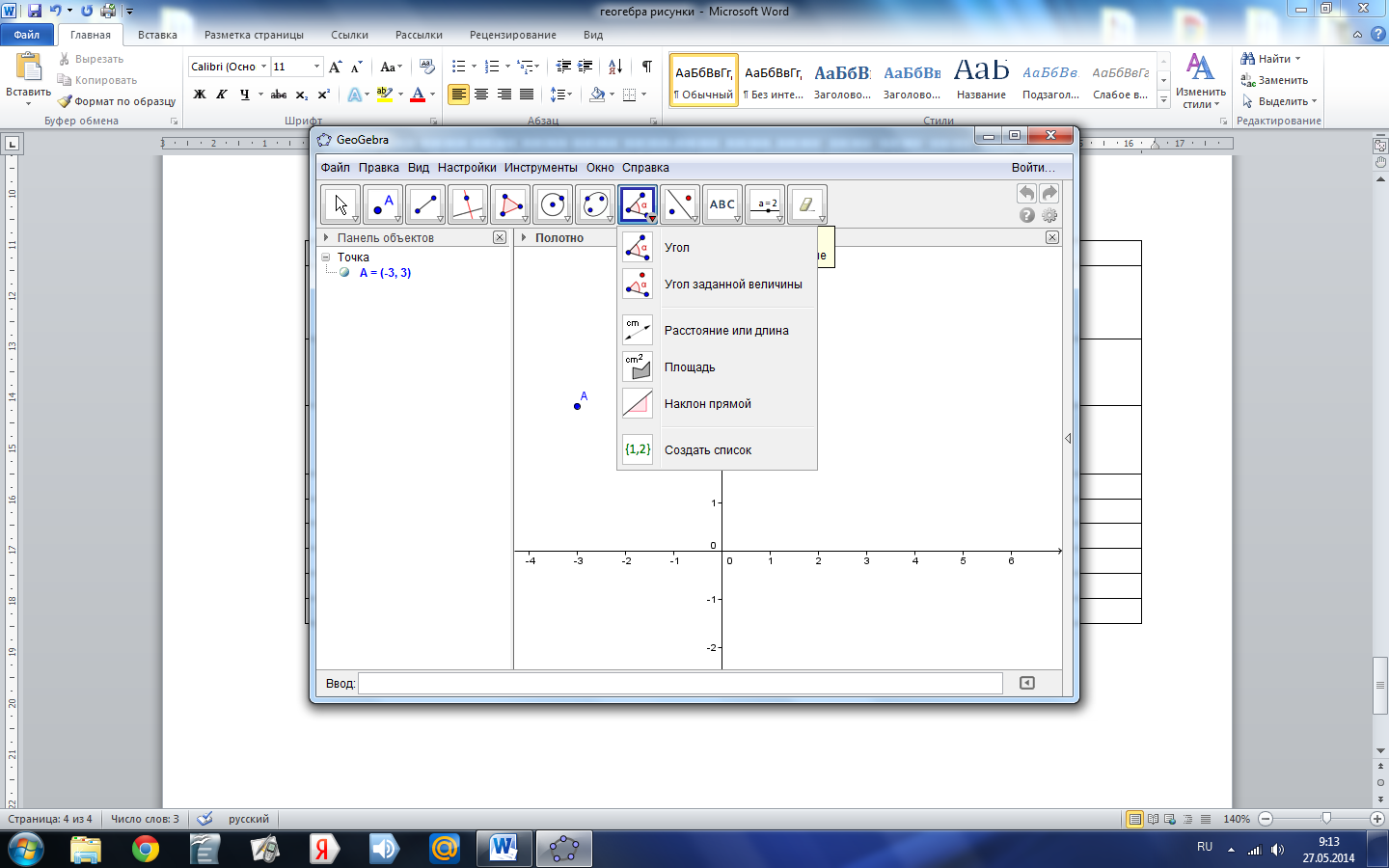	Отрезок	Нажмите на Графический вид два раза или по двум уже существующим точкам.
	Удалить	Нажмите на объект для его удаления.
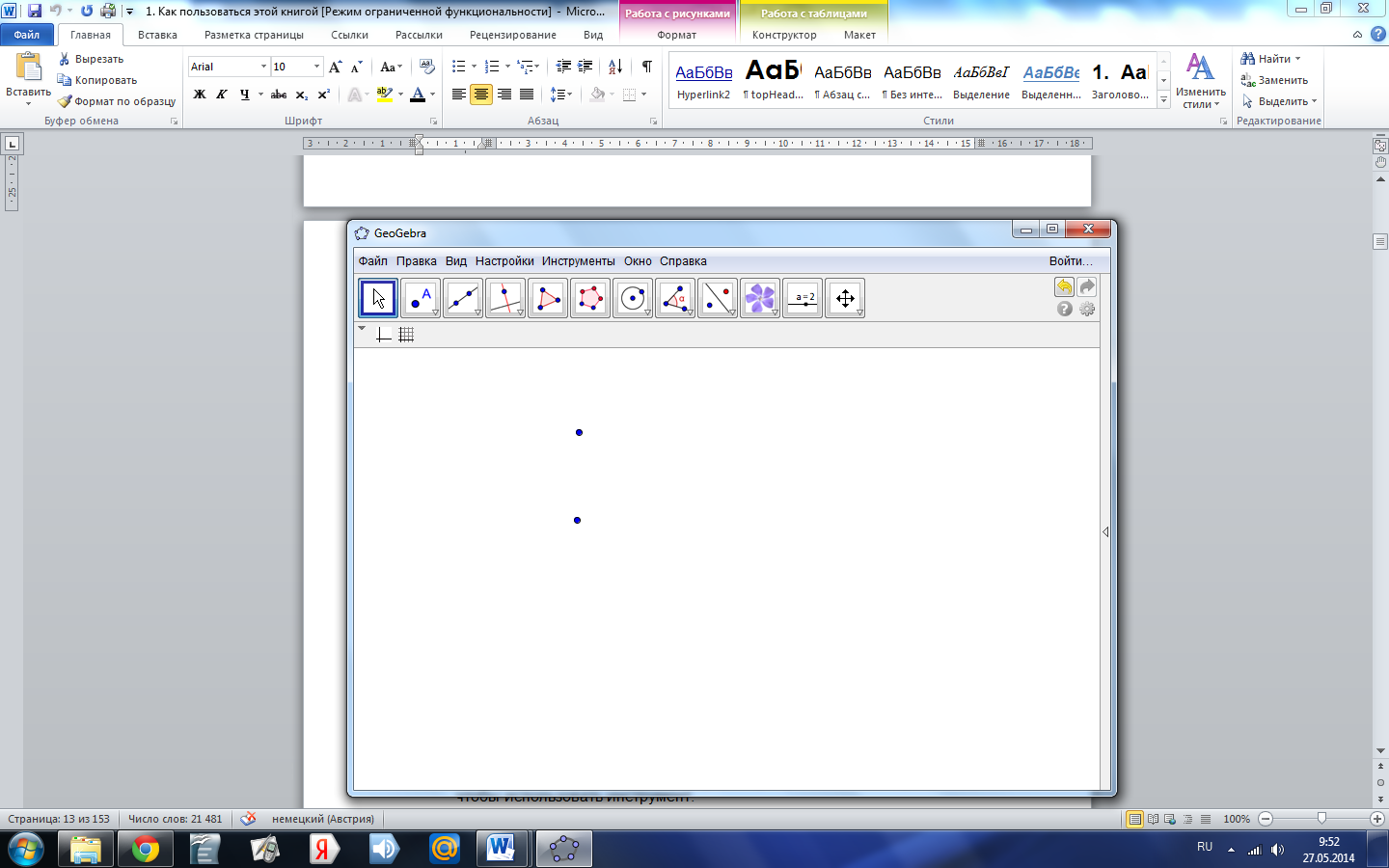	Отмена/Повтор	Отмена / Повтор построения шаг за шагом.
	Переместить чертеж	Щелкните и перетащите чертеж или ось с нажатой клавишей Shift.
	Увеличить/Уменьшить	Щелкните по графику, чтобы увеличить или уменьшить масштаб.

Ход работы

1. Загрузить программу GeoGebra.
2. Открыть файл «мой первый рисунок.ggb» (рис.7).
3. Откройте пустой интерфейс GeoGebra в том же окне.
4. Щелкните по стрелке в правой части Графического Вида и выберите Элементарная геометрия с боковой панели .
5. Создайте свой первый чертеж идентичный файлу «мой первый рисунок.ggb». Дополнительные рисунки представлены в приложении 2 (Приложение 2).

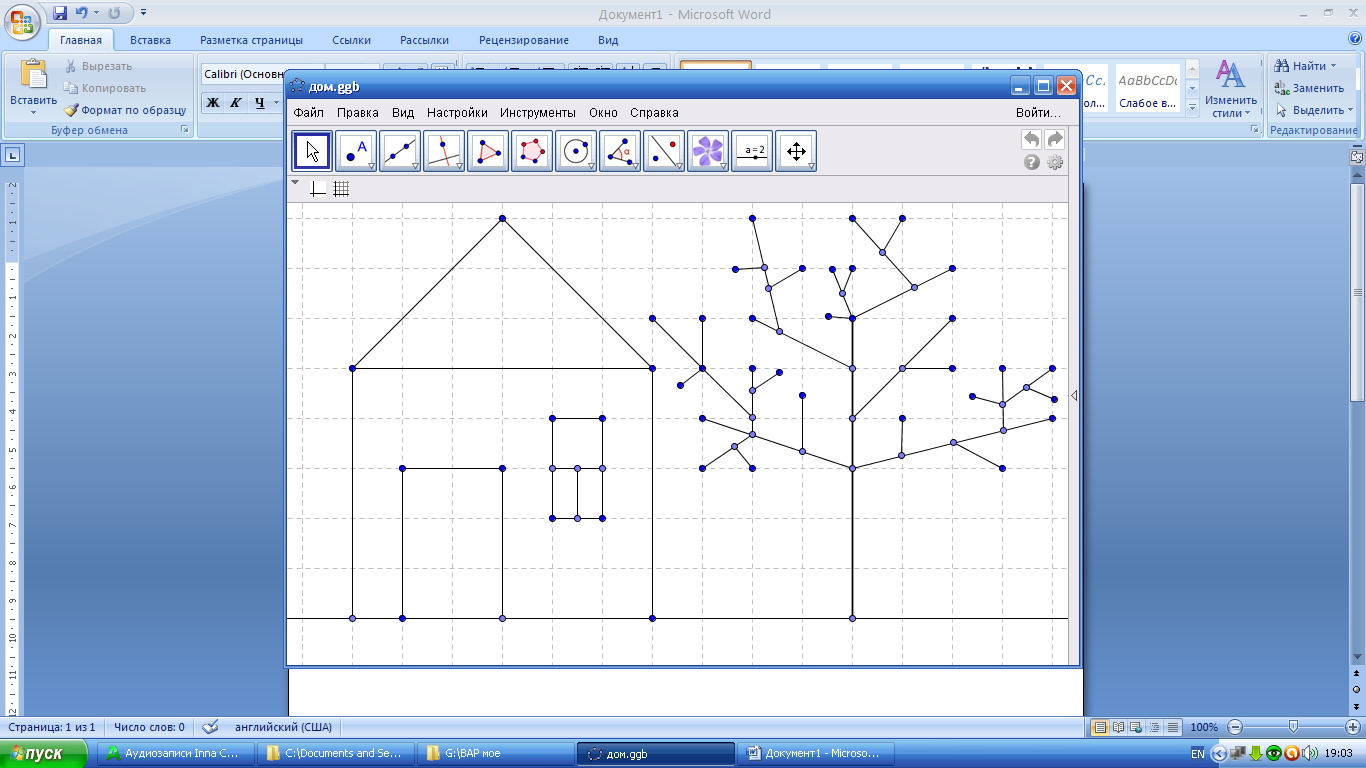Рис.7. Пример первого чертежа в программе GeoGebra.

1. Используйте мышь и следующий выбор инструментов для того, чтобы преобразовать числа в Графический Вид (например, квадрат, прямоугольник, дом, дерево и т.д.).
2. Сохранить файл на рабочем столе под своей Фамилией в папке «5-А».

Источник: kopilkaurokov.ru