Глава 1, «Приступая к работе» описывает первые шаги до начала использования ELCUT. В этой главе Вы узнаете, как установить программу на Ваш компьютер, как её при необходимости можно удалить, системные требования.
Глава 2, «Первое знакомство» кратко описывает организацию пакета ELCUT и содержит обзор основных типов решаемых задач.

- Скачать электронную версию:
Печатный формат
Дата: 27 ноября 2021
Глава 3, «Описание задачи» объясняет, как указать тип задачи и её основные свойства.
Глава 4, «Описание геометрии задачи» рассказывает, как описать геометрию задачи, построить сетку конечных элементов, задать свойства материалов и граничные условия.
Глава 5, «Ввод параметров задачи» описывает организацию файлов физических свойств и то, как эти файлы связаны с объектами геометрической модели.
Электрическая бытовая розетка. Пример работы в ELCUT.
Глава 6, «Схемы электрических цепей» описывает работу с редактором цепей.
Глава 7, «Решение задач» рассказывает, как запустить процесс решения задачи и получить результаты решения.
Глава 8, «Анализ результатов решения» содержит описание всестороннего анализа результатов решения задачи в ELCUT.
Глава 9, «Работа с трехмерными задачами» знакомит с особенностями постановки, описания, решения и просмотра результатов трехмерных задач.
Глава 10, «Надстройки» описывает возможности расширения функциональности ELCUT с помощью дополнительных модулей.
Глава 11, «Теоретическое описание» содержит математическое описание всех типов задач, решаемых с помощью ELCUT. Прочтите эту главу, чтобы узнать, может ли ELCUT решить Вашу задачу.
Профессиональная версия программы имеет такой же интерфейс и общую организацию, что и Студенческая версия. Следует только помнить об ограничении в 255 узлов для сетки конечных элементов в Студенческой версии.
Источник: elcut.ru
Решение двухмерных полевых задач в программе ELCUT
Программа ELCUT позволяет производить решение двухмерных полевых задач методом конечных элементов.
В качестве примера, достаточно наглядного и простого для усвоения студентами, рассмотрим расчёт электрического поля электротехнического устройства.
Пусть необходимо средствами программы ELCUT рассчитать электростатические характеристики конденсатора с параллельными обкладками (рис. 1.1). Разность потенциалов между обкладками 200 V.

Рис. 1.1. Исследуемая модель
Первоначально необходимо оценить конструкцию. В нашем случае, конденсатор имеет две обкладки и находится в воздухе.
Внешней оболочкой или экраном необходимо охватить всю конструкцию устройства. Данное условие связано с методом расчета, который применяется в данной программе. Это метод конечных элементов, который требует наличия области, в которой локализовано электрическое поле.
Моделирование теплопередачи в ELCUT Студенческий
Запускаем программу ELCUT. В меню Файл выбираем пункт Создать. В появившемся окне Создание нового документа выбрать пункт ЗадачаELCUTи нажать кнопку OK> (рис. 1.2).

Рис. 1.2. Создание нового документа
В окне Создание задачи ввести имя файла задачи в соответствующей строке (рис. 1.3).

Рис. 1.3. Создание задачи
Нажать кнопку Next>. В следующем окне выбрать тип задачи Электростатика, класс модели плоская и параметр расчета обычный(рис. 1.4).

Нажать кнопку Next>. В следующем окне выбрать единицы длины миллиметры, систему координат декартовы координаты (рис. 1.5).

Рис. 1.5. Выбор системы координат
Нажать кнопку Finish>. Интерфейс программы будет выглядеть следующим образом (рис. 1.6).

Рис. 1.6. Интерфейс программы
Раскрыть при помощи левой кнопки мыши все пункты списка в левом окне (рис. 1.7).

Рис. 1.7. Пункты списка левого окна
Произвести двойной щелчок на пункте Геометрия: расчет конденсатора.mod. При этом появится консоль с предложением (рис. 1.8).

Рис. 1.8. Диалоговое окно
Нажать на кнопку OK>.
В правой части окна появится файл геометрии, который рекомендуется сохранить с расширением .modв той же папке, где создана задача.
Приступить к рисованию плоской модели конденсатора. Для этого достаточно изобразить две обкладки без выводов. На панели модели нажатьВставить вершины/ребра(рис. 1.9).

Рис. 1.9, Панель рисования модели
Протягивая при помощи левой кнопки мыши линию, изобразить две обкладки конденсатора. Геометрические размеры легко определить, зная текущие координаты курсора, которые указываются в нижней части файла модели. Для изменения масштаба надо использоватьУвеличить или Уменьшить на панели модели.
Охватываем всю конструкцию устройства экраном, в которой локализовано электрическое поле (рис. 1.10).

Рис. 1.10. Геометрическая модель
В нашей конструкции один блок (воздух), в котором находятся две обкладки конденсатора и экран, таким образом, конструкция включает в себя три ребра.
После создания геометрии необходимо ввести свойства всех ребер, блоков и, если это необходимо, вершин.
Для создания метки блока необходимо нажать на панели модели кнопку Выделение объектов. После этого сделать двойной щелчок левой кнопкой мыши внутри области расчета (рис. 1.11).

Рис. 1.11. Создание блоков модели
В разделе Метка написать «воздух» (рис. 1.12).

Рис. 1.12. Создание метки блока
При этом в правой части окна программы появится метка воздух в разделе Метки блоков(рис. 1.13).

Рис. 1.13. Метка блока
Делаем двойной щелчок левой кнопкой мыши по метке воздух в браузере и вводим параметр Относительная диэлектрическая проницаемость, равный 1. Диэлектрик изотропный, т.е. его свойства не зависят от координаты(рис. 1.14).

Рис. 1.14. Свойства метки блока
Как видно, рассматриваемая геометрия системы состоит из шести ребер. Для корректного расчета полей необходимо обозначить все блоки и ребра. Для связи меток ребер и блоков с файлом геометрии на каждом элементе конденсатора произвести щелчок правой кнопкой мыши и выбрать пункт Свойства либо сделать двойной щелчок левой кнопкой мыши (рис. 1.15).

Рис. 1.15. Ввод свойств метки ребер
В разделе Метка выставить необходимую метку блока, ребра или вершины. Выпадающее меню, необходимое для настройки свойств выделенных объектов, выглядит следующим образом(рис. 1.16).

Рис.1.16. Выпадающее меню
Свойства остальных объектов настраиваются аналогично.
Для построения сетки в области расчета необходимо нажать на предпоследнюю кнопку панели инструментов (рис. 1.17).

Рис. 1.17. Сетка в области расчета
Далее можно приступить к расчету. Для этого в меню Правка выбратьРешить задачу (рис. 1.18).

Рис. 1.18. Решение задачи
Далее приведём результаты моделирования.Изолинии потенциала представлены на рис. 1.19.

Рис. 1.19. Изолинии потенциала
Векторное поле напряженности электрического поляпредставлено на рис. 1.20.

Рис. 1.20. Векторное поле напряженности электрического поля
Векторное поле электрического смещения представлено на рис. 1.21.

Рис. 1.21. Векторное поле электрического смещения
Векторное поле плотности энергии представлено на рис. 1.22.

Рис. 1.22. Векторное поле плотности энергии
Для построения картины полей необходимо произвести щелчок правой кнопкой мыши на полученном рисунке и выбрать необходимую физическую величину, распределение которой требуется получить (рис. 1.23).

Рис. 1.23. Распределение физических величин
Используя инструмент Локальные значения, можно получить информацию о значениях физических величин в любой точке (рис. 1.24).

Рис. 1.24. Результат расчета
При анализе результатов моделирования можно сравнить такие параметры электрического поля исследуемого электротехнического устройства, как напряжённость, электрическое смещение, плотность энергии и др. (рис. 1.25).
На основании моделирования электрических полей можно делать выводы и рекомендации по конструктивной оптимизации электротехнических устройств.
Рекомендуем самостоятельно ознакомиться с расчётом двухмерных магнитных полей по методике, подобно рассмотренной выше.
электрический поле геометрический elcut

Рис. 1.25. Результаты моделирования
Источник: studwood.net
Как работать в программе elcut
Настоящая статья посвящена рассмотрению возможности применения программного продукта ELCUT для разработки магнитного компенсатора жесткости на неодимовых магнитах. Данный продукт представляет собой достаточно точный программный аппарат для решения задач магнитостатики. Решение этих задач является важнейшим этапом на стадии проектирования и расчета магнитного компенсатора жесткости, так как первоначально необходимо найти тяговую силу взаимодействия между магнитом и магнитными материалами для обеспечения нужной падающей силовой характеристики компенсатора. В статье приведены построенные модели неодимовых магнитов, спроектирована картина поля, представлены картины распределения и направления векторов напряженности и индукции магнитных полей. Полученные в ходе моделирования результаты в дальнейшем будут использоваться для проектирования и создания магнитного компенсатора жесткости на супермагнитах.

неодимовые магниты
магнитное поле
компенсатор жесткости
1. Гурова Е.Г. Виброизолирующие подвески транспортных энергетических установок с нелинейными электромагнитными компенсаторами жесткости. – Новосибирск: Издательство НГТУ, 2012. – 156 c.
2. Гурова Е.Г., Резниченкина А.Д. Тяговая характеристика супермагнитного компенсатора жесткости // Фундаментальные исследования. – 2015. – № 8–3. – С. 506–508.
3. Долженко В.Н. Шум и вибрация: учеб. пособие / В.Н. Долженко, А.А. Фортыгин, В.С. Фокин и др. – М.: РГОТУПС, 2003. – 50 с.
4. Дубицкий С.Д., Поднос В.Г. ELCUT – инженерная система моделирования двумерных физических полей // CADmaster. – 2001. – № 1. – С. 17–21.
5. Сливинская А.Г. Электромагниты и постоянные магниты: учеб. пособие / А.Г. Сливинская; отв. ред. М.Г. Бородина. – М.: Энергия, 1972. – 248 с.
6. Gurova E.G., Gurov M.G. Vibro isolator with neodymium magnets compensator of the stiffness // Applied Mechanics and Materials. – 2014. – Vol. 682: Innovative Technologies and Economics in Engineering. – P. 118–121.
По теории виброизоляции устройства, направленные на снижение механических колебаний, должны работать согласно эффекту нулевой жесткости, согласно которой идеальная виброизоляция абсолютно твердого тела от произвольных пространственных колебаний будет обеспечена, если в любой момент времени суммы проекций всех приложенных к нему сил на произвольные оси координат и суммы моментов относительно этих осей координат равны нулю [1]:
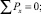
(1)
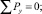
(2)
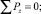
(3)
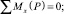
(4)
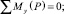
(5)
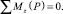
(6)
Для обеспечения участка нулевой жесткости в пределах размаха колебаний, виброизоляторы должны состоять из упругого элемента и параллельно включенного компенсатора жесткости, обладающего падающей силовой характеристикой той же жесткости, что и упругий элемент, но с обратным знаком. Таким образом, линейно нарастающая характеристика компенсируется убывающей под тем же углом относительно оси абсцисс. Это приведет к тому, что при любых пространственных перемещениях вибрирующего объекта относительно защищаемого будут соблюдаться условия (1)–(6).
В настоящее время существует много различных конструкций корректоров жесткости, представленных в разных исполнениях, основанных на принципах механики, гидравлики, пневматики [3]. Однако наиболее эффективным следует считать электромагнитный компенсатор жесткости, т.к. он обладает множеством преимуществ над предлагаемыми ранее: автоматическая подстройка на изменяющуюся нагрузку, отсутствие сил трения и дополнительной инерции.
При всех своих достоинствах применение такого компенсатора жесткости затруднительно из-за значительных габаритов и дополнительного источника энергии. В [2, 6] предложено заменить основные составляющие в компенсаторе жесткости, а именно: электромагнитные катушки с сердечниками на неодимовые магниты, которые представляют собой редкоземельные постоянные магниты, состоящие из сплава неодим-железо-бор. Применение составляющих, обладающих магнитными свойствами, приводит к необходимости решения задач магнитостатики. Для решения подобных задач представляется возможным использовать программный продукт «ELCUT» компании ООО «TOR».
Для построения точной тяговой характеристики компенсатора жесткости на постоянных магнитах необходимо произвести моделирование в программной среде «ELCUT». Создание модели компенсатора позволит с допустимой погрешностью определить силу взаимодействия полей магнитов. Дальнейшее моделирование при различной величине воздушного зазора между телами позволит нам определить силу, действующую на якорь при различных его перемещениях относительно неодимовых магнитов. Эти данные станут основой для построения необходимой силовой падающей характеристики компенсатора жесткости относительно положений якоря на оси.
Данная программа позволяет проводить инженерный анализ и моделировать методом конечных элементов (МКЭ) как двухмерные, так и трехмерные модели различных магнитов, а также компенсаторов жесткости на их основе. Возможности «ELCUT» позволяют определить необходимые свойства и параметры магнитных полей как электромагнитов, так и постоянных магнитов [5]. Данная программа рассматривает неодимовый магнит как элемент, обладающий магнитной проницаемостью, коэрцитивной силой и остаточной индукцией. В системе можно найти напряженность магнитного поля в любой точке пространства около моделируемого объекта, его индукцию, силу и ее направление методом интегрирования по контуру элемента. Одновременно с вышеперечисленным имеется возможность построения графиков изменения индукции, напряженности, магнитной проницаемости и количества энергии вдоль пространственной оси [4].
Используем компьютерную программу «ELCUT» для моделирования цилиндрического неодимового магнита марки N42 и анализа его магнитных свойств.
При моделировании использованы исходные данные:
радиус магнита (стального цилиндра): 2,25 см;
высота магнита (стального цилиндра): 2 см;
остаточная магнитная индукция: 1,36 Т;
коэрцитивная сила магнита: 955 кА/м;
относительная магнитная проницаемость среды: 1;
относительная магнитная проницаемость стали: 1000;
расстояние между магнитом и магнитом (сталью): 1 см.
Первый шаг при моделировании магнитной системы элементов компенсатора жесткости – это построение магнитного поля элементов. На рис. 1, 3, 4 представлены форма и величина магнитных полей, создаваемых: неодимовым магнитом, взаимодействием магнита, стального цилиндра и двух магнитов. На рисунках приведены модели цилиндрических тел, представленных с помощью области с магнитной проводимостью, коэрцитивной силой и остаточной индукцией, причем нижняя граница представляет собой ось вращения этих тел, что позволяет моделировать участок магнитных тел, а полученный результат представляет собой параметр, справедливый для всего тела.
Из рис. 1, 3, 4 видно, что картина магнитного поля в зависимости от параметрических данных изменяется: один магнит, взаимодействие со стальным цилиндром или другим подобным магнитом. Это обусловлено разницей магнитных проводимостей, а также распределением векторов индукции и напряженности, создаваемыми составляющими устройств.
Рассмотрим подробнее эти задачи. Система моделирования «ELCUT» позволяет представить вектор магнитной индукции для одного магнита, а также представить график распределения магнитной индукции вдоль оси. Результаты представлены на рис. 1, 2.
График зависимости, представленный на рис. 2, позволяет заранее рассчитать величину индукции магнитного поля вдоль оси или по контуру. Также можно построить модель поля, создаваемого двумя одинаковыми магнитами со встречно направленными векторами индукции и напряженности магнитного поля, результаты представлены на рис. 3. На основе данной модели можно получить направление и величину векторов индукции и напряженности, а также силы, действующей на эти магниты. Для получения результатов выполнено моделирование двух магнитов по представленным ранее параметрам, с измененным направлением коэрцитивной силы одного из магнитов.
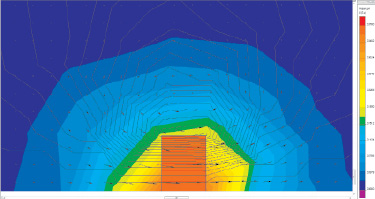
Рис. 1. Распределение и векторы магнитной индукции
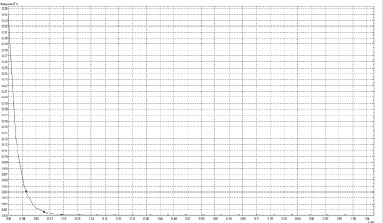
Рис. 2. График распределения магнитной индукции вдоль оси цилиндрического магнита
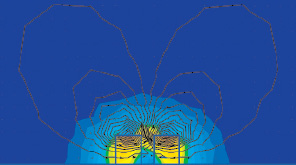
Рис. 3. Распределение и направление векторов индукции
Параметры, получаемые из программы, – точные данные взаимодействия двух магнитов, которые позволяют достаточно точно подобрать необходимое количество магнитов для создания нужной силы их взаимодействия (отталкивания/притяжения), что позволяет подобрать упругие элементы необходимой жесткости для создания компенсатора жесткости с необходимыми характеристиками.
При моделировании магнитов данная программная система позволяет исследовать ферромагнитные материалы, такие как железо и сталь. Результаты моделирования взаимодействия стального цилиндра и неодимового магнита представлены на рис. 4, 5. На этих рисунках показаны линии магнитного поля, создаваемого при взаимодействии магнита и стали, также изображены векторы индукции и напряженности магнитного поля. Данная модель, как и предыдущая, позволяет определить направление и величину вектора силы взаимодействия стали и магнита.
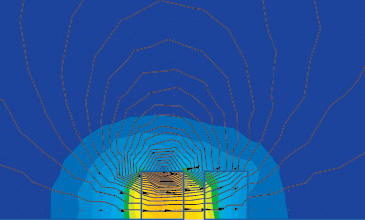
Рис. 4. Распределение и векторы магнитной индукции поля магнита и стального цилиндра
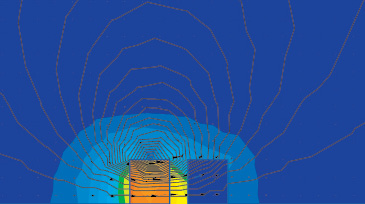
Рис. 5. Распределение и векторы напряженности поля магнита и стального цилиндра
На приведенных рисунках видны линии сетки элементов, построенные в программе. Данная сеть элементов строится автоматически и является основой для решения задач магнитостатики методом конечных элементов. Суть этого метода заключается в том, что область, для которой решаются дифференциальные уравнения, разбивается на конечное количество подобластей (элементов).
В каждом из элементов произвольно выбирается вид аппроксимирующей функции. В простейшем случае это полином первой степени. Вне своего элемента аппроксимирующая функция равна нулю. Значения функций на границах элементов (в узлах) являются решением задачи.
Исходя из результатов исследований, можно сделать вывод, что программный продукт «ELCUT» эффективен для использования решения задач магнитостатики, к которым и относится разработка компенсатора жесткости на неодимовых магнитах. Полученные данные при моделировании взаимодействия различных магнитных элементов станут одной из основ для проектирования компенсаторов жесткости на неодимовых магнитах.
Работа проводится при поддержке гранта РФФИ № 14-01-31386 мол_а.
Источник: fundamental-research.ru