Как построить математическую модель программы

— составить систему ограничений с учетом дисциплинирующих факторов задачи.

Рассмотрим пример построения простейшей математической модели: задачи о планировании производства.

Предприятие производит изделия трех видов: U1,U2,U3. По каждому виду изделий известен план: b1,b2,b3. План может быть перевыполнен, но в определенных границах: не более p1,p2,p3 единиц соответственно.

На изготовление изделий идет какое-то сырье. Всего имеется 4 вида сырья: S1,S2,S3,S4, причем, запасы сырья ограничены числами y1,y2,y3,y4 соответственно. Для изготовления единицы изделия i-го вида (i=1,3) требуется A[i,j] единиц сырья j-го вида (j=1,4). При реализации единицы изделия i-го вида получают прибыль Сi.

Требуется так спланировать производство, чтобы план был выполнен или перевыполнен, но при отсутствии затоваривания, а суммарная прибыль обращалась бы в максимум.

Для удобства условие задачи запишем в таблицу

Изделие	Сырьё	План выпуска	Условие спроса	Прибыль с реализацией
S1	S2	S3	S4
U1	A11	A12	A13	A14	B1	β1	C1
U2	A21	A22	A23	A24	B2	β2	C2
U3	A31	A32	A33	A34	B3	β3	C3
Запасы сырья	γ1	γ2	γ3	γ4

Как построить математическую модель оптимизационной задачи

I. Определим, что будет являться элементами решения.

В нашем примере это будет количество выпускаемых изделий каждого типа

Обозначим их через х1, х2, х3 соответственно.

II. Целевой функцией будет максимальная прибыль от реализации. Запишем ее в виде уравнения:

III. Составим ограничения (дисциплинирующие условия)

а) с учетом выполнения плана

б) с учетом условия спроса

в) с учетом запасов сырья и нормы расходов.

Целевая функция (1) с ограничениями (2)- (4) и представляют математическую модель задачи.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник: studopedia.ru

Построение математических моделей в прикладных задачах

Крымская, Ю. А. Построение математических моделей в прикладных задачах / Ю. А. Крымская, Е. И. Титова, С. Н. Ячинова. — Текст : непосредственный // Молодой ученый. — 2013. — № 12 (59). — С. 3-6. — URL: https://moluch.ru/archive/59/8532/ (дата обращения: 10.07.2023).

К основным целям обучения математике относится формирование умений строить математические модели простейших реальных явлений, исследовать явления по заданным моделям, конструировать приложения моделей. Одним из средств реализации этой цели является метод математического моделирования.

Математическая модель задачи. Как составить. Математическая постановка. Исследование операций.

Под математическим моделированием, в узком смысле слова, понимают описание в виде уравнений и неравенств реальных физических, химических, технологических, биологических, экономических и других процессов. Для того чтобы использовать математические методы для анализа и синтеза различных процессов, необходимо уметь описать эти процессы на языке математики, то есть описать в виде системы уравнений и неравенств. При построении модели используются такие операции мышления, как анализ через синтез, сравнение, классификация, обобщение, которые способствуют его развитию. Составление математической модели, перевод задачи на язык математики готовит студентов к моделированию реальных процессов и явлений в их будущей профессиональной деятельности. Особую роль математическое моделирование играет в экономической и научной сфере деятельности.

Рассмотрим применение математического моделирования при решении транспортных задач в экономике, а также математическую модель в задачах по теории цепей Маркова, в теории вероятностей. Чем и покажем значение математического моделирования в разных областях.

1. Математическое моделирование в экономике. Математическая модель транспортной задачи является математической моделью задачи линейного программирования. Среди множества решений системы ограничений необходимо найти такое неотрицательное решение, при котором целевая функция принимала бы минимальное значение.

Как и любая другая задача линейного программирования, транспортная задача может быть решена при помощи симплекс-метода. Благодаря особому устройству системы ограничений общая процедура симплекс-метода в применении к транспортной задаче сильно упрощается. Хотя для транспортной задачи существуют несколько весьма простых и удобных методов отыскания начального допустимого решения (опорного плана). Транспортные задачи закрытого типа, когда запас груза на базах совпадает с объемом потребности предприятий, решаются двумя методами: северо-западного угла и минимальной стоимости. Транспортные задачи открытого типа, когда запасы превышают потребности или наоборот, сводятся к задачам закрытого типа путем введения фиктивного пункта назначения (в случае превышения груза на базах над общими потребностями предприятий) или фиктивного поставщика (в случае превышения спроса над запасами на базах).

Отметим, что процесс моделирования состоит из следующих этапов: 1) перевод предложенной задачи на язык математических терминов, то есть построение математической модели задачи (формализация); 2) решение задачи (решение внутри модели); 3) перевод полученного результата (математического решения) на язык, на котором была сформулирована исходная задача (интерпретация полученного решения).

Наиболее ответственным и сложным является первый этап — построение математической модели. Оно осуществляется логическим путем на основе анализа изучаемого явления (процесса) и требует умения описать явление (процесс) на языке математики.

Второй этап — этап решения задачи в рамках математической теории можно еще назвать этапом математической обработки формальной модели. Он является решающим в математическом моделировании. Именно на этом этапе применяются все математические методы (логические, алгебраические, геометрические и т. д.) для формального вывода следствий из исходных допущений модели.

На стадии математической обработки рассматриваются абстракции. Этот этап представляет собой дедуктивное ядро моделирования. На последнем этапе моделирования полученные выводы проходят через еще один процесс перевода — с языка математики обратно на естественный язык. Всё выше сказанное проиллюстрируем примером.

Пример. На базах имеется запас сырья необходимого для производства четырех предприятий. На первой базе — 60 т., на второй — 90 т., на третьей — 140 т. Первому предприятию для производства требуется 40 т. сырья, второму — 30 т., третьему — 100 т., четвертому — 120 т. Найти оптимальный план задачи методом северо-западного угла, зная, что стоимость перевозок с первой базы на первое предприятие равна 4 ед., на второе — 2 ед., на третье — 3 ед., на четвертое — 4 ед., со второй базы на первое предприятие равна 2 ед., на второе — 4 ед., на третье — 3 ед., на четвертое — 5 ед., с третьей базы на первое предприятие равна 6 ед., на второе — 5 ед., на третье — 4 ед., на четвертое — 6 ед.

I этап. Формализация. Построим математическую модель задачи в виде таблицы:

Источник: moluch.ru

Особенности построения математических моделей

Аннотация: В лекции описан процесс построения математической модели. Приведен словесный алгоритм процесса.

Для использования ЭВМ при решении прикладных задач прежде всего прикладная задача должна быть «переведена» на формальный математический язык, т.е. для реального объекта, процесса или системы должна быть построена его математическая модель .

Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи .

Для построения математической модели необходимо:

1. тщательно проанализировать реальный объект или процесс;
2. выделить его наиболее существенные черты и свойства;
3. определить переменные, т.е. параметры, значения которых влияют на основные черты и свойства объекта;
4. описать зависимость основных свойств объекта, процесса или системы от значения переменных с помощью логико-математических соотношений (уравнения, равенства, неравенства, логико-математические конструкций);
5. выделить внутренние связи объекта, процесса или системы с помощью ограничений, уравнений, равенств, неравенств, логико-математических конструкций;
6. определить внешние связи и описать их с помощью ограничений, уравнений, равенств, неравенств, логико-математических конструкций.

Математическое моделирование , кроме исследования объекта, процесса или системы и составления их математического описания, также включает:

1. построение алгоритма, моделирующего поведение объекта, процесса или системы;
2. проверка адекватности модели и объекта, процесса или системы на основе вычислительного и натурного эксперимента;
3. корректировка модели;
4. использование модели.

Математическое описание исследуемых процессов и систем зависит от:

1. природы реального процесса или системы и составляется на основе законов физики, химии, механики, термодинамики, гидродинамики, электротехники, теории пластичности , теории упругости и т.д.
2. требуемой достоверности и точности изучения и исследования реальных процессов и систем.

На этапе выбора математической модели устанавливаются: линейность и нелинейность объекта, процесса или системы, динамичность или статичность, стационарность или нестационарность, а также степень детерминированности исследуемого объекта или процесса. При математическом моделировании сознательно отвлекаются от конкретной физической природы объектов, процессов или систем и, в основном, сосредотачиваются на изучении количественных зависимостей между величинами, описывающими эти процессы.

Математическая модель никогда не бывает полностью тождественна рассматриваемому объекту, процессу или системе. Основанная на упрощении, идеализации , она является приближенным описанием объекта. Поэтому результаты, полученные при анализе модели, носят приближенный характер. Их точность определяется степенью адекватности (соответствия) модели и объекта.

Построение математической модели обычно начинается с построения и анализа простейшей, наиболее грубой математической модели рассматриваемого объекта, процесса или системы. В дальнейшем, в случае необходимости, модель уточняется, делается ее соответствие объекту более полным.

Возьмем простой пример. Нужно определить площадь поверхности письменного стола. Обычно для этого измеряют его длину и ширину, а затем перемножают полученные числа. Такая элементарная процедура фактически обозначает следующее: реальный объект (поверхность стола) заменяется абстрактной математической моделью – прямоугольником. Прямоугольнику приписываются размеры, полученные в результате измерения длины и ширины поверхности стола, и площадь такого прямоугольника приближенно принимается за искомую площадь стола.

Однако модель прямоугольника для письменного стола – это простейшая, наиболее грубая модель. При более серьезном подходе к задаче прежде, чем воспользоваться для определения площади стола моделью прямоугольника, эту модель нужно проверить. Проверки можно осуществить следующим образом: измерить длины противоположных сторон стола, а также длины его диагоналей и сравнить их между собой. Если, с требуемой степенью точности, длины противоположных сторон и длины диагоналей попарно равны между собой, то поверхность стола действительно можно рассматривать как прямоугольник . В противном случае модель прямоугольника придется отвергнуть и заменить моделью четырехугольника общего вида. При более высоком требовании к точности может возникнуть необходимость пойти в уточнении модели еще дальше, например, учесть закругления углов стола.

С помощью этого простого примера было показано, что математическая модель не определяется однозначно исследуемым объектом, процессом или системой. Для одного и того же стола мы можем принять либо модель прямоугольника, либо более сложную модель четырехугольника общего вида, либо четырехугольника с закругленными углами. Выбор той или иной модели определяется требованием точности. С повышением точности модель приходится усложнять, учитывая новые и новые особенности изучаемого объекта, процесса или системы.

Рассмотрим другой пример: исследование движения кривошипно-шатунного механизма (Рис. 2.1).

Рис. 2.1.

Для кинематического анализа этого механизма, прежде всего, необходимо построить его кинематическую модель. Для этого:

1. Заменяем механизм его кинематической схемой, где все звенья заменены жесткими связями ;
2. Пользуясь этой схемой, мы выводим уравнение движения механизма;
3. Дифференцируя последнее, получаем уравнения скоростей и ускорения, которые представляют собой дифференциальные уравнения 1-го и 2-го порядка.

Запишем эти уравнения:

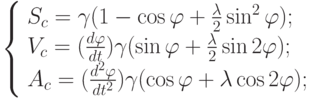
где С0 – крайнее правое положение ползуна С:

r – радиус кривошипа AB;

l – длина шатуна BC;

– угол поворота кривошипа;

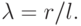
Полученные трансцендентные уравнения представляют математическую модель движения плоского аксиального кривошипно-шатунного механизма, основанную на следующих упрощающих предположениях:

1. нас не интересовали конструктивные формы и расположение масс, входящих в механизм тел, и все тела механизма мы заменили отрезками прямых. На самом деле, все звенья механизма имеют массу и довольно сложную форму. Например, шатун – это сложное сборное соединение, форма и размеры которого, конечно, будут влиять на движение механизма;
2. при построении математической модели движения рассматриваемого механизма мы также не учитывали упругость входящих в механизм тел, т.е. все звенья рассматривали как абстрактные абсолютно жесткие тела. В действительности же, все входящие в механизм тела – упругие тела. Они при движении механизма будут как-то деформироваться, в них могут даже возникнуть упругие колебания. Это все, конечно, также будет влиять на движение механизма;
3. мы не учитывали погрешность изготовления звеньев, зазоры в кинематических парах A, B, C и т.д.

Таким образом, важно еще раз подчеркнуть, что, чем выше требования к точности результатов решения задачи, тем больше необходимость учитывать при построении математической модели особенности изучаемого объекта, процесса или системы. Однако, здесь важно во время остановиться, так как сложная математическая модель может превратиться в трудно разрешимую задачу.

Наиболее просто строится модель, когда хорошо известны законы, определяющие поведение и свойства объекта, процесса или системы, и имеется большой практический опыт их применения.

Более сложная ситуация возникает тогда, когда наши знания об изучаемом объекте, процессе или системе недостаточны. В этом случае при построении математической модели приходится делать дополнительные предположения, которые носят характер гипотез, такая модель называется гипотетической. Выводы, полученные в результате исследования такой гипотетической модели, носят условный характер. Для проверки выводов необходимо сопоставить результаты исследования модели на ЭВМ с результатами натурного эксперимента. Таким образом, вопрос применимости некоторой математической модели к изучению рассматриваемого объекта, процесса или системы не является математическим вопросом и не может быть решен математическими методами.

Основным критерием истинности является эксперимент, практика в самом широком смысле этого слова.

Построение математической модели в прикладных задачах – один из наиболее сложных и ответственных этапов работы. Опыт показывает, что во многих случаях правильно выбрать модель – значит решить проблему более, чем наполовину. Трудность данного этапа состоит в том, что он требует соединения математических и специальных знаний. Поэтому очень важно, чтобы при решении прикладных задач математики обладали специальными знаниями об объекте, а их партнеры, специалисты, – определенной математической культурой, опытом исследования в своей области, знанием ЭВМ и программирования.

Источник: intuit.ru