С помощью данной программы можно онлайн нарисовать любой граф (ориентированный, неориентированный, с петлями), сетевой график, дерево, граф состояний или блок-схему. Во вкладке Примеры графов можно ознакомиться с возможностями онлайн сервиса.
Граф можно нарисовать или задать в виде матрицы или схемы (меню Действия ).
- Поиск кратчайшего пути с помощью алгоритма Дейкстры, задача о кратчайшем пути (см. вкладку Параметры графа ).
- Построить дерево.
- Построить дерево по коду Прюфера (затем можно будет найти его инверсию).
- Редактор графа
- Параметры графа
- Решение
- Примеры реализаций
- Оформление Word
Нумерация вершин с №1 ?
Дуги с одинаковыми весами: ?
Видеоинструкция
Соединить Свойства Удалить
- Сохранить
- Загрузить
- Добавить в виде матрицы
- Добавить в виде схемы
- Очистить полотно
- Фильтр для всех
- Сохранить как docx
- Сохранить как png
- Обратный граф
- Разрез сети
- Преобразовать в дерево
- ✍ Помощь в решении задач
Размеры графического полотна
Ширина Высота
Как построить матрицу смежности?
Созданный граф можно сохранить в форматах docx и png (меню Действия ). Далее можно найти характеристики графа (матрица смежности, матрица инциденций, матрица расстояний).
Для сформированного графа можно выполнить следующие действия:
Здесь будет показано решение
В этом разделе собраны примеры, иллюстрирующие возможности редактора графов.
Граф состояний кредитной карты
Здесь объектом анализа выступает такой банковский продукт как кредитная карта K . На графе состояний операций по кредитной карте отмечены следующие события: начисления процентов на остаток счета ( P — петля), покупка П на сумму S , возврат CashBack в виде бонусных баллов на счет карты.
Сетевой график получения кредитной истории
1 — устройство на работу с трудовой книжкой; 2 , 3 — получение кредитной карты с минимальным кредитным лимитом. Некоторые банки выдают кредиты уже после 3 -х месячного трудового стажа, другие банки устанавливают этот срок от 1 года; 4 , 5 — продвинутый уровень , получение кредитных карт с большим cashback-ом; 6 — хорошая кредитная история, полученная с выгодой от использования кредитных карт.
Схема транспортной сети
На схеме показаны взаимное расположение пунктов, длинны звеньев, потребность грузов в развозочной системе.
Задача календарного планирования с заданной технологией
Здесь показан пример ориентированного графа
Схема канала распределения
Товар после изготовления поступает в оптовую продажу, далее доходит либо до потребителя, либо следует в розничную продажу, а затем уже к потребителю. По данной схеме работают и продуктовые рынки.
Еще один пример построения схемы классификации аннуитетных платежей можно посмотреть здесь.
Видеоинструкция
Инструкция к сервису по рисованию графа
Для добавления вершины на графическое полотно необходимо использовать соответствующую фигуре кнопку Добавить . Если название вершины не задано, будет показан ее номер. По умолчанию, нумерация начинается с номера 1 . Чтобы нумерация начиналась с 0 , необходимо снять отметку с пункта Нумерация вершин с №1 . Название вершины может содержать символьную строку (перенос строк осуществляется через символ | ).
Gephi создание графа
Чтобы соединить вершины, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить . Если выбрана одна вершина, то будет создана петля. У выбранных элементов (вершин или дуг) можно изменить свойства или удалить их.
Построенный граф можно сохранить в формате docx или png .
Основные определения
В математической теории графов и информатике граф представляет собой совокупность объектов со связями между ними. Граф G задается множеством точек (вершин) X=1,…,xn> и множеством линий (ребер) A=1,…,am> , соединяющих между собой все или часть этих точек. На данный момент в сервисе для графического отображения вершин используются следующие фигуры: круг, квадрат и треугольник. Каждая вершина может иметь собственный вид: цвет и толщина линии, фон и размеры . Для изменения характеристик вершины необходимо выделить ее левой кнопки мыши и нажать на кнопку Свойства .
Ребра графа – линии, соединяющие вершины. Чтобы соединить вершины, необходимо выбрать одну или две из них. Каждое ребро графа имеет собственные свойства: цвет и толщина линии, значение (отображается поверх ребра).
Ребро графа называется неориентированным, если порядок расположения его концов (направление стрелок) в графе не принимается во внимание. Ребро графа называется ориентированным, если этот порядок существенен. Ориентированное ребро называют также дугой графа. Две вершины, соединённые дугой или ребром называются смежными. Для задания дуги необходимо при соединении вершин отметить пункт концевой маркер → . Для изменения типа дуги необходимо выделить ее левой кнопки мыши и нажать на кнопку Свойства .
С каждым ребром можно связать число или символ — вес ребра. Для задачи коммивояжера это может быть расстояние между городами, а для транспортной сети — стоимость проезда. Такой граф называется взвешенным.
Для каждого графа G(Х) существует обратный граф G -1 (Х) , полученный изменением ориентации каждого из ребер графа G(Х) на противоположную.
Петлей называется ребро g(xi,xi) , у которого начальная и конечная вершины совпадают. Петля обычно считается неориентированной. Для создания петли необходимо выделить только одну вершину и нажать на кнопку Соединить .
Ребра ориентированного графа с одинаковыми весами могут быть представлены в разном виде. Для настройки отображения используйте пункт Дуги с одинаковыми весами .
В неизменном виде: отображается каждая дуга с весом.
Источник: www.semestr.online
Программирование на C, C# и Java
Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
Программа для построения графов C#
Представляем вашему вниманию программу для построения графов, написанную на языке C#. Внизу страницы вы можете скачать исходник этой программы, а в этой статье будут описаны функции программы и основные приемы, использовавшиеся при их кодировании.
Структура пользовательского интерфейса
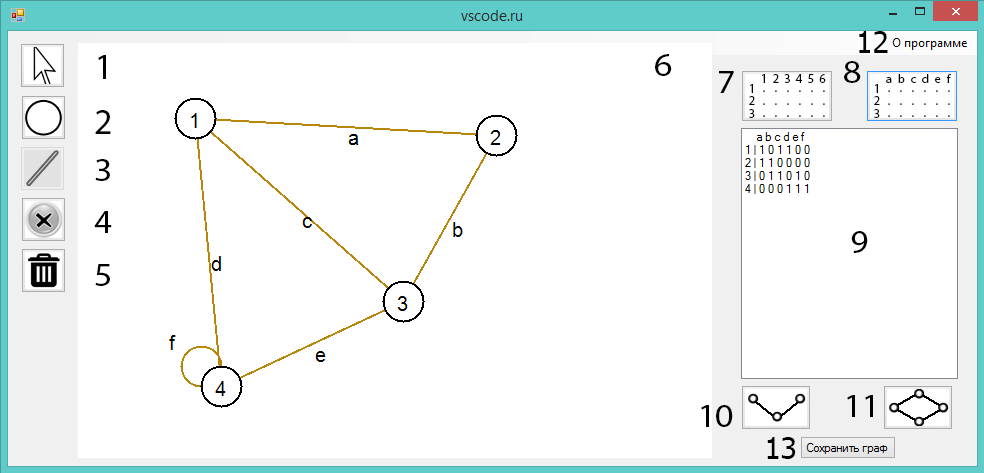
Рисунок 1. Пользовательский интерфейс программы
Пользовательский интерфейс программы изображен на рисунке 1. На нем цифрами обозначены элементы управления:
- Выбор вершины (при выборе какой-либо вершины, отображается ее степень).
- Создание вершины.
- Создание ребра.
- Удаление элемента.
- Удаление всего графа.
- Рабочее поле для построения графа.
- Построение матрицы смежности.
- Построение матрицы инцидентности.
- Поле для вывода информации о графе: степень выбранной вершины, матриц смежности и инцидентности, элементарных цепей и циклов.
- Вывод всех элементарных цепей.
- Вывод всех элементарных циклов.
- Информация о программе (окно представлено на рисунке 2).
- Сохранение изображения графа.
Если при построении ребра вы выбрали не ту вершину, то отменить выбор можно, нажав правой кнопкой мыши на выбранной вершине.

Рисунок 2. Окно «О программе»
Описание структуры программы
Опишем ключевые моменты в программном коде.
При кодировании граф был представлен в виде списка (List<>) экземпляров класса Vertex (вершина):
class Vertex
public int x , y ;
public Vertex ( int x , int y )
this . x = x ;
this . y = y ;
где x и y — координаты центра вершины.
И списка (List<>) экземпляров класса Edge (ребро):
class Edge
public int v1 , v2 ;
public Edge ( int v1 , int v2 )
this . v1 = v1 ;
this . v2 = v2 ;
v1 и v2 — номера вершин, которые соединяет ребро.
Когда происходит выбор вершины мышью, поиск нужной вершины из списка осуществляется посредством перебора всех вершин и проверки условия принадлежности точки, в месте щелчка мыши, окружности вершины с помощью уравнения окружности: (x — x0) 2 + (y — y0) 2 = R 2 .
for ( int i = 0 ; i < V . Count ; i ++ )
if ( Math . Pow ( ( V [ i ] . x — e . X ) , 2 ) + Math . Pow ( ( V [ i ] . y — e . Y ) , 2 ) < = G . R * G . R )
где e.X, e.Y — координаты точки в месте щелчка мыши, а G.R — радиус окружности вершины.
Заполнение матрицы смежности:
public void fillAdjacencyMatrix ( int numberV , List < Edge >E , int [ , ] matrix )
for ( int i = 0 ; i < numberV ; i ++ )
for ( int j = 0 ; j < numberV ; j ++ )
matrix [ i , j ] = 0 ;
for ( int i = 0 ; i < E . Count ; i ++ )
matrix [ E [ i ] . v1 , E [ i ] . v2 ] = 1 ;
matrix [ E [ i ] . v2 , E [ i ] . v1 ] = 1 ;
numberV — количество вершин в графе. matrix имеет размер [numberV, numberV].
Заполнение матрицы инцидентности:
public void fillIncidenceMatrix ( int numberV , List < Edge >E , int [ , ] matrix )
for ( int i = 0 ; i < numberV ; i ++ )
for ( int j = 0 ; j < E . Count ; j ++ )
matrix [ i , j ] = 0 ;
for ( int i = 0 ; i < E . Count ; i ++ )
matrix [ E [ i ] . v1 , i ] = 1 ;
matrix [ E [ i ] . v2 , i ] = 1 ;
где numberV — количество вершин в графе. matrix имеет размер [numberV, E.Count].
Определение степени вершины происходит в результате суммирования элементов строки матрицы смежности с номером, равным номеру выбранной вершины.
Если нажата кнопка «удаление элемента», то при щелчке мышью на рабочем поле происходит перебор всех элементов графа и поиск элемента, которому принадлежит координата в месте щелчка. При этом для ребер и петель поиск осуществляется с допуском в несколько пикселей, то есть, например, принадлежность точки, в месте щелка, конкретному ребру характеризуется принадлежностью точки области, границами которой выступают прямые, отстоящие вверх и вниз от исходной прямой на несколько пикселей.
Проиллюстрировать вышесказанное можно с помощью рисунка:
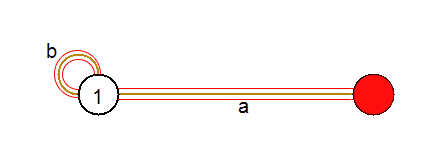
Рисунок 3. Области, рассматриваемые при поиске элемента графа для удаления
Красным цветом обозначен тот самый допуск в несколько пикселей при поиске элемента для удаления. Для вершины никакого допуска рассматривать не нужно.
Про поиск элементарных цепей и циклов мы уже рассказывали на vscode.ru. Почитать можно здесь:
Скачать исходник программы, написанной в Visual Studio, можно, нажав на кнопку ниже.
Источник: vscode.ru
Строим интерактивные графы с помощью NetworkX и Plolty

Думаю, каждый Data Scientist знаком с библиотекой matplotlib, однако это не единственная библиотека для визуализации в python. Бывают такие задачи, когда нужна более “живая” визуализация и нет времени на написание кода для идеального графика с ее помощью. Тогда на ум приходит Plotly (ссылка: https://plotly.com/python/).
Plotly — это открытая библиотека, с помощью которой можно быстро строить красивые, а главное интерактивные графики прямо в jupyter-notebook. Данная разработка основывается на JavaScript-библиотеке D3.js. К плюсам данной библиотеки можно отнести связь к одним из удобнейших веб-фреймворком Dash, который появился недавно с помощью создателей Plotly.
Графы, пожалуй, идут в числе первых изображений в matplotlib, которые нуждаются в интерактивности. В нашем случае с помощью интерактивных графов можно получить достаточно много инсайдов из данных. В связку к Plotly мы добавим одну из самых популярных библиотек для работы с графами — NetworkX (ссылка: https://networkx.org/). Данная библиотека создана на python и предназначена для работы с сетевыми структурами и также является бесплатной.
Сочетание Plotly и NetworkX открывает для нас огромные возможности для отличной визуализации графов. В данной статье мы построим визуализацию, на которой будет изображен граф, размеры узла которого будут зависеть от количества его связей, а при наведении курсора на узел будем показывать количеств этих самых связей.
Импортируем нужные библиотеки.
import plotly.graph_objects as go import networkx as nx
Создадим граф, который возвращает случайный граф, вершины которого будут располагаться в единичном кубе. Два узла соединяются ребром, если расстояние между узлами не превышает определенного радиуса.
G = nx.random_geometric_graph(100, 0.125)
Отрисуем самым обычным способом в NetworkX, чтобы сравнить с графом, который отрисуем чуть позже.
nx.draw(G, node_size = 10)

Соберем координаты для дальнейшего построения связей на графике с помощью Plotly. Добавим их на график.
edge_x = [] edge_y = [] for edge in G.edges(): x0, y0 = G.nodes[edge[0]][‘pos’] x1, y1 = G.nodes[edge[1]][‘pos’] edge_x.append(x0) edge_x.append(x1) edge_x.append(None) edge_y.append(y0) edge_y.append(y1) edge_y.append(None) edge_trace = go.Scatter( x = edge_x, y = edge_y, line = dict(width = 0.5, color = ‘#888’), hoverinfo = ‘none’, mode = ‘lines’)
Проделаем аналогичную операцию для узлов.
node_x = [] node_y = [] for node in G.nodes(): x, y = G.nodes[node][‘pos’] node_x.append(x) node_y.append(y) node_trace = go.Scatter( x = node_x, y = node_y, mode = ‘markers’, hoverinfo = ‘text’, marker = dict( color = [], size = 10 ), line_width = 2)
Добавим той самой интерактивности нашему графу. При наведении курсора на узел он будет показывать количество связей с другими узлами. Также размер маркера узла будет зависеть от количества связей.
Для некоторых задач это позволит найти наиболее “дружелюбные” элементы графа. В целом, можно добавить очень много полезной и ценной информации, допустим, номер узла или инициалы человека, если использовать графы в контексте задач, связанных с взаимодействием людей.

node_adjacencies = [] node_text = [] for node, adjacencies in enumerate(G.adjacency()): node_adjacencies.append(len(adjacencies[1])) node_text.append(‘Connections: ‘ + str(len(adjacencies[1]))) node_trace.marker.size = node_adjacencies node_trace.text = node_text
Далее нарисуем полученный граф и посмотрим на результат.
fig = go.Figure(data=[edge_trace, node_trace], layout=go.Layout( title=’
Тестовый граф для NTA’, titlefont_size = 16, showlegend = False, xaxis=dict(showgrid = False, zeroline = False, showticklabels = False), yaxis=dict(showgrid = False, zeroline = False, showticklabels = False)) ) fig.show()

Данную визуализацию можно сохранить в HTML и изучать уже без использования python, что является огромным плюсом в работе с Plotly, ведь не всегда люди, которым для анализа нужны данные графы, уверенно владеют python. Отдельно стоит отметить верхнюю панель для навигации по графу, она включает в себя все самое нужное: увеличение/уменьшение области просмотра, сохранение участка графика в png, а также выделение определенных областей для более точного исследования.

В конце хочется сказать, что тандем этих двух библиотек позволяет закрыть почти все потребности в повседневной работе с графами.
Источник: newtechaudit.ru