Как посчитать выживаемость в программе статистике

Переменная Hospital в файле данных Heart.sta есть (фиктивная) группирующая переменная, которая идентифицирует больницу, в которую пациент был принят для проведения трансплантации сердца. В этом исследовании представлены три больницы: Hillview (код 1 ), St_Andreas (код 2 ), and Biner (код 3 ). На основе сравнения функций выживания в этих трех больницах применением некоторых двувыборочных критериев из модуля Анализ выживаемости можно сделать выводы, как о выживаемости пациентов, так и о возможностях этих тестов. Спецификация анализа Откройте файл данных Heart.sta через меню Файл — Открыть; скорее всего, он будет располагаться в каталоге /Examples/Datasets системы STATISTICA . Затем выберите Анализ выживаемости из меню Анализ — Углубленные методы анализа для отображения стартовой панели модуля Анализ выживаемости . Дважды щелкните по строке Сравнение нескольких выборок , чтобы открыть диалоговое окно Сравнение выживаемости в нескольких группах . Нажмите кнопку Переменные , чтобы появилось стандартное окно Выберите переменные . Выберите первые 6 переменных в качестве Времен жизни (1, 2 или 6) . STATISTICA будет интерпретировать первую и четвертую переменные в этом списке как месяцы, вторую и пятую — как дни, а третью и шестую — как год. Далее необходимо определить переменную Censored как Цензурирующую переменную и переменную Hospital как Группирующую переменную. Нажмите кнопку OK для возвращения в диалоговое окно Сравнение выживаемости в нескольких группах . Дважды щелкните по полю ввода Код для полных наблюдений , чтобы появилось диалоговое окно Переменная 7 . Здесь выберите Complete и нажмите OK . Затем дважды щелкните по полю Код для цензурированных наблюдений и выберите Censored . Чтобы ввести коды для группирующей переменной, нажмите кнопку Коды (для групп) и потом в диалоговом окне сначала нажмите кнопку Все (чтобы отобрать все коды), а потом щелкните OK (чтобы ввести эти коды и завершить этот диалог). Диалоговое окно Сравнение выживаемости в нескольких группах теперь выглядит следующим образом:

Видеоурок: Построение кривой выживаемости

Теперь, чтобы продолжить, достаточно щелкнуть OK , и откроется диалоговое окно Результаты сравнения выживаемости в нескольких группах . Критерий хи — квадрат дает почти значимое отклонение в этом примере ( p <.06). Отсюда мы можем сделать предварительное заключение, что имеются определенные различия между больницами. Чтобы увидеть эти различия, мы можем построить графики функций выживания для различных групп, для чего достаточно нажать кнопку Кумулятивная доля выживших по группам .

Ясно видно, что функция выживания в больнице города Бинер медленнее уменьшается на начальном участке времени по сравнению с другими больницами. Отсюда мы можем заключить, что по какой — то причине пациенты с трансплантированным сердцем в больнице Бинера имеют больше шансов выживания, в частности в течение критических первых 100 дней после трансплантации.

Вернитесь к диалоговому окну Результаты сравнения выживаемости в нескольких группах и нажмите на вкладку Дополнительно . Чтобы просмотреть таблицы времен жизни для этих трех больниц, нажмите кнопку Процент выживших по группам . Появятся отдельные электронные таблицы для каждой больницы. Данные таблицы подтверждают приведенное выше заключение.

Анализ Выживаемости Таблицы выживаемости (life table) survival analysis

Сравнение выживаемости в двух группах Модуль Анализ выживаемости содержит различные методы для сравнения двух выборок. Нажмите кнопку Отмена в диалоговом окне Результаты сравнения выживаемости в нескольких группах и в диалоговом окне Сравнение выживаемости в нескольких группах для возвращения в стартовую панель. Выберите опцию Сравнение двух выборок на стартовой панели, чтобы появилось окно Сравнение выживаемости в двух группах . Нажмите кнопку Переменные для задания всех переменных, как и ранее (см. выше). Также укажите Код для полных наблюдений и Код для цензурированных наблюдений , как и ранее.

Чтобы сравнить группы, дважды щелкните по полю ввода Код для первой группы для отображения диалогового окна Переменная 11 . Выберите здесь первую группу для сравнения (в нашем примере выбрана Hillview ) и нажмите OK . Потом дважды щелкните по полю ввода Код для второй группы и выберите Biner . Диалоговое окно Сравнение выживаемости в двух группах теперь выглядит следующим образом: Теперь нажмите кнопку OK , чтобы перейти к диалоговому окну Двувыборочные критерии . В данном примере некоторые из критериев демонстрируют уровень значимости p около 0.05, в то время как другие — незначимы. Поэтому с некоторой долей уверенности мы можем заключить, что выживаемости пациентов с трансплантированным сердцем в этих двух больницах отличаются значимо, притом в больнице Бинера выживаемость выше. http://www.statsoft.ru/home/portal/applications/medicine/example5.htm

2. Модель Кокса с зависящими от времени ковариатами Знаменитая модель Кокса, предложенная в 1972 году, интенсивно используется в самых различных областях, особенно в медицине и страховании, для оценки условного риска заболевания при заданных значениях исходных признаков Модель Кокса основана на предположении, что функцию риска (или функцию интенсивностей отказов, выражаясь на техническом сленге), можно факторизовать, т.е. представить в виде произведения двух функций: h(t) = h 0 (t) y (z 1 ,…,z m ), где h 0 (t) — базовая функция интенсивности , зависящая, например, от возраста пациента или от времени, прошедшего после осмотра, y (z 1 ,…, z m ) — функция изучаемых признаков, например, пол пациента, семейное положение или время года, класс отеля, страна поездки, если речь идет о туроператорских рисках. В технических приложениях признаками могут быть, например, температура окружающей среды, сезон, уровень влажности.

В общем случае функция признаков, как и сами признаки, выбираются из соображений предметной области и целей исследования. Часто модель записывается в следующем виде: h[(t),(z 1 , z 2 , . z m )] = h 0 (t)*exp(b 1 *z 1 +. + b m *z m ). Базовая функция интенсивности h 0 (t) может рассматриваться теперь как функция интенсивности при равенстве нулю всех независимых переменных или ковариат.

Общая задача состоит в том, чтобы по наблюдениям за временами жизни оценить h 0 и неизвестные коэффициенты b 1 . b m . Модель можно линеаризовать последнюю модель, поделив обе части соотношения на h 0 (t) и взяв натуральный логарифм от обеих частей: log = b 1 *z 1 +. + b m *z m Факторизованная модель обладает тем замечательным свойством, что оценки ее параметров требуется не столько много наблюдений, как потребовалось бы для не факторизованной модели. Существенное в этой модели то, что зависимость является мультипликативной. Это предположение иногда называется гипотезой пропорциональности . Покажем, как проверить эту гипотезу. Пример основан на данных Pike (1966) времен жизни двух групп крыс, одна из которых контрольная, а другая подвергалась воздействию канцерогена.

Предположим, что у вас есть сомнение в гипотезе пропорциональности, то есть об отсутствии зависящих от времени ковариат. Идея проверки гипотезы очень проста. Рассмотрим еще одну модель, более общую, чем модель пропорциональных интенсивностей, и с помощью критерия хи — квадрат сравним их. Более общая модель функции интенсивности содержит как постоянную (не зависящую от времени) ковариату (в данном примере Группа — Group ), так и зависящую от времени ковариату (в данном примере ковариату, определяемую как: Group*Log (время) — 5.4 — Group*Log (Time) — 5.4) . Значение 5.4 использовано лишь из соображений нормировки, для того, чтобы среднее значение логарифма времени жизни было приближенно равно 5.4. Проверку проведем в модуле Анализ выживаемости. Задание анализа Откройте файл с данными Pike.sta . Выберите анализ Регрессионные модели . В предлагаемом списке моделей выберите Модель Кокса с зависящими от времени ковариатами .

В этом анализе зависимая переменная Времена жизни (переменная 1) — Survival (variable 1) , индикатор цензурирования Censored . Поскольку, по умолчанию, код для цензурированных наблюдений тот же самый, что используется в файле данных, то остается задать только ковариаты. Диалоговое окно имеет редактируемые поля.

Левая часть поля ( Ковариата ) может быть использована, чтобы ввести метку для ковариаты. Правая ( Выражение ) может быть использована для определения ковариаты с помощью арифметического выражения. В данном анализе мы, на самом деле, будем рассматривать 2 модели: первая модель с постоянными ковариатами, вторая модель с зависящими от времени ковариатами. Введите переменные этих моделей, сделав установки, как показано на рисунке: Нажмите OK , откройте диалоговое окно Оценивание регрессионной модели . Приняв в этом диалоге все условия по умолчанию, просто нажмите OK , чтобы перейти к оцениванию параметров моделей.

Нажмите OK и из диалогового окна Результаты регрессии выберите опцию Оценки параметров . В таблице показаны оценки параметров двух моделей. Обе модели значимы (см. уровни значимости в последнем столбце), но как показывает критерий хи — квадрат в заголовке таблицы между моделями значимого отличия нет (хи — квадрат = 2.89, число степеней свободы = 2, р = 0.23527). http://www.statsoft.ru/home/portal/applications/medicine/med2.htm 3. Множественный анализ выживаемости Данные по множественным отказам или многомерной выживаемости часто встречаются в биомедицинских и прочих исследованиях. Эти данные возникают в исследовании времени до появления нескольких событий для одного объекта, или времени до появления одинаковых событий для связанных объектов (например, для родственников или одноклассников). В таких исследованиях критические события коррелированны друг с другом, нарушая требование независимости классического анализа выживаемости. Различают два принципиальных случая: критические события рассматриваются для одного объекта в определенном порядке (например, регресс заболевания ) и критические события разных типов, которые нельзя считать независимыми: например, побочные эффекты в одной группе по лечению ( treatment ).

Простейший подход к анализу таких данных – исследовать время до первого события, игнорируя остальные эффекты. Обычно такой подход неадекватен и приводит к потере дополнительной информации, потому в последнее время становятся популярны два подхода: модели с уязвимостью ( frailty models ) и модели с поправкой на корреляции факторов.

В первой модели связь между событиями реализуется как случайный фактор с известным типом распределения, обычно гамма со средним 1 и неизвестной дисперсией, она не будет рассмотрена в этой главе. Во втором подходе зависимости между критическими событиями исключены из модели, вместо этого используется корреляция оценок.

Чаще всего используются оценки, полученные из модели пропорциональных рисков Кокса. Вычислительные методы Пусть 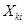, 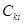– время события и цензурирования для k — го типа событий и i — го объекта (события и объекты понимаются в обоих смыслах).

Введем 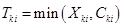и 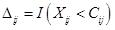, 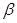— вектор регрессионных коэффициентов. Интенсивность будет равна 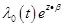в первом и 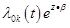во втором случае.

Целевые коэффициенты 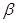оцениваются методом максимума правдоподобия. Модель для неупорядоченных событий. События одного типа. Пример В качестве примера смоделируем исследование эффективности фотокоагуляции при лечении диабетической ретинопатии. Подобные задачи возникают при изучении семейных заболеваний.

У каждого из испытуемых из группы риска один случайно выбранный глаз был подвержен фотокоагуляции (воздействию), второй глаз оставлен в контрольной группе. Цель исследования – показать, что профилактика значимо влияет на заболевание и увеличивает время до потери зрения.

Переменная ID указывает на семью испытуемого, TREAT – на тип глаза («контрольный» или «исследуемый»), N – номер пациента, CENS – индикатор цензурирования. На каждого пациента в таблице приходится по две строки: «контрольный» глаз (TREAT = 0) и «исследуемый» (TREAT = 1); в переменной CENS указано произошло ли поражение сетчатой оболочки глазного яблока к моменту завершения исследования, в переменной TIME указано время (в годах), которое пациент состоял на учете до наступления события, N – идентификатор пациента, ID – идентификатор семьи. Задача состоит в том, чтобы показать, что потеря зрения глазом, на который оказано воздействие, наступает позже, чем у глаза без терапевтического лечения. Воспользуемся регрессионной моделью Кокса со временами жизни, факторами и цензурированием:

Источник: studfile.net

Анализ выживаемости в системе Statistica (стр. 1 из 5)

Методы анализа выживаемости (Survival Analisis) первоначально были развиты в медицинских, биологических исследованиях и страховании, но затем стали шароко применяться в социальных и экономических науках, а также в промышленности в инженерных задачах (анализ надежности и время отказов)

Одной из важных характеристик, описывающих течение болезни, является продолжительность жизни пациентов с момента поступления в клинику или после проведения операции. В принципе, для описания средних времен жизни и сравнения новой методики со старой можно использовать стандартные статистические методы. Однако рассматриваемые данные имеют специфику, которую следует учитывать. Дело в том, что в медицинской практике мы часто имеем дело с неполными данными.

Это связано с тем, что трудно наблюдать все время жизни пациента после операции, так как пациент мог быть выписан или переведен в другую клинику и связь с ним была утеряна. При этом мы располагаем не полной информацией о времени жизни пациента, а лишь частичной.

Естественное желание исследователя использовать все данные, т. е. анализировать как полные времена жизни, так и неполные, и не терять с трудом собранную информацию. Для этого и предназначены методы анализа выживаемости, которые позволяют изучать неполные или цензурированные данные. Наблюдения, которые содержат неполную информацию, называются неполными или цензурированными (например, «пациент А был жив по крайней мере 4 месяца после того, как был переведен в другую клинику и контакт с ним был потерян»). Это пример цензурированного наблюдения: информация о том, что пациент был жив 4 месяца, важна и может быть использована для построения оценок. Наблюдения от момента операции до летального исхода называется полными.

Итак, в анализе выживаемости различают полные (по-английски complete) и неполные, или цензурированные, наблюдения (по-английски censored). Конечно, можно было использовать только полные времена жизни, но тогда мы имели бы в своем распоряжении очень мало наблюдений и соответственно неточные оценки. Использование, наряду с полными наблюдениями, неполных или цензурированных наблюдений является главной особенностью методов анализа выживаемости.

I.Таблицы времён жизни

1.1. Исходные данные

Данные о пациентах, перенесших операцию на сердце

Источник: smekni.com

Анализ выживаемости

Анализ выживаемости (Survival Analysis) — это статистический метод исследования времени, которое проходит до наступления события, такого как конец, разрушение или отказ. Он также называется анализом времени до события или анализом времени жизни.

Анализ выживаемости имеет широкое применение в медицине, биологии, экономике и других областях исследования. Например, в медицинских исследованиях анализ выживаемости используется для оценки эффективности нового лекарства, чтобы определить время, пока пациенты не умрут или не получат рецидив заболевания. В других областях, например, в экономике, анализ выживаемости может использоваться для оценки времени до наступления банкротства компании.

Основная идея анализа выживаемости заключается в том, что мы можем изучать время, которое проходит до наступления события, даже если не наблюдаем каждый случай. Например, мы можем изучать время, которое проходит до смерти человека, даже если не наблюдаем каждый случай смерти.

Анализ выживаемости использует специальные статистические методы, которые позволяют учитывать, что не все события происходят одновременно, и что наблюдения могут быть незавершенными. В результате, мы можем оценить вероятность происхождения события в конкретный момент времени и построить кривую выживаемости, которая показывает вероятность выживания с течением времени.

Основные термины

1. Функция выживаемости — это один из основных терминов, используемых в анализе выживаемости. Она представляет собой функцию, которая определяет вероятность выживания на протяжении определенного периода времени.

Функция выживаемости S(t) определяется как вероятность того, что событие не наступит до момента времени t :

где T — случайная величина, представляющая время до наступления события.

Например, если рассматривать функцию выживаемости в контексте заболевания, то S(t) показывает вероятность того, что пациент не умирает от заболевания до момента времени t . Если функция выживаемости имеет значение 0.8 для момента времени t=5 лет, это означает, что вероятность выживания пациента в течение пяти лет после диагностики равна 0.8.

Функция выживаемости является ключевым показателем в анализе выживаемости. Из нее можно получить другие показатели, такие как функция риска и функция кумулятивной доли выживших. Функция выживаемости также может быть использована для исследования влияния различных факторов на выживаемость, таких как возраст, пол, заболевание и т.д.

2. Функция риска — это вероятность наступления события в конкретный момент времени t , при условии, что оно не наступило до этого момента. Зачастую функция риска называется интенсивностью наступления событий. Она может быть представлена в виде линейной функции, экспоненциальной функции или более сложных моделей.

Функция риска может использоваться для прогнозирования риска наступления событий в будущем. В медицинской статистике, например, функция риска может быть использована для прогнозирования вероятности развития заболевания у пациента, основываясь на его медицинской истории и других факторах.

Функция также может быть использована для сравнения риска наступления событий между двумя или более группами. Например, в исследованиях лекарственных препаратов, функция риска может быть использована для сравнения эффективности лекарства с плацебо.

3. Функция кумулятивной доли выживших — это сумма вероятностей выживания до моментов времени t . Иначе говоря, это доля людей или объектов, которые еще не столкнулись со смертью или другим событием до определенного прошедшего момента времени t .

Функция кумулятивной доли выживших может быть использована для представления того, как изменяется количество выживших с течением времени, что может быть важно для медицинских исследований, анализа безопасности оборудования, оценки надежности и других задач.

Функция кумулятивной доли выживших может быть представлена в виде графика, где по оси x отложено время, а по оси y — доля выживших, показывающая, как изменяется количество выживших в зависимости от времени.

4. Цензурирование переменных в анализе выживаемости является важной техникой при работе с данными, связанными с выживаемостью. Оно используется, когда не все наблюдения из выборки имеют полные данные о продолжительности выживания. В таких случаях наблюдения могут быть цензурированные.

Цензурирование переменных в анализе выживаемости происходит в нескольких случаях. Например, когда время выживания больного неизвестно, но мы знаем, что он жив и на момент обработки данных. В этом случае, запись о пациенте может быть цензурированной. То есть, мы знаем, что данный пациент выжил до определенного момента времени, но не знаем точно, сколько времени он еще проживет. Кроме того, цензурирование могут применяться в случае, когда пациенты выбыли из выборки, но некоторые данные оставшихся пациентах все еще можно использовать в анализе.

Цензурирование переменных в анализе выживаемости может быть односторонним или двусторонним. В одностороннем случае мы можем предположить, что пациенты умирают только после какого-то определенного времени. В этом случае, цензурирование будет производиться, если продолжительность жизни больного превышает определенный порог. В двустороннем случае мы можем предположить, что пациенты умирают только при определенных условиях. В этом случае, цензурирование будет производиться, если продолжительность жизни больного находится в определенном диапазоне.

Методы анализа выживаемости

1. Метод Каплан-Мейера — это статистический метод для определения вероятности того, что событие не наступит до определенного момента времени. Он используется для анализа выживаемости, особенно в медицинских исследованиях, чтобы определить, сколько пациентов еще живет после определенного момента времени.

Для построения кривой выживаемости по методу Каплан-Мейера, сначала выборка разбивается на группы по какому-то признаку (например, лечение пациента). Затем для каждой группы определяется доля пациентов, которые еще не умерли на каждом промежутке времени.

Примером может служить исследование выживаемости пациентов с диагнозом рак легкого, которые прошли хирургическое лечение. Группы могут быть разбиты по таким факторам, как возраст, плохие привычки, наличие метастазов. Кривые выживаемости для каждой группы показывают, какая доля пациентов еще жива в течение определенного периода времени после лечения. По результатам исследования будет произведено сравнение кривых выживаемости для каждой группы и выявлены факторы, оказывающие влияние на выживаемость пациентов.

2. Метод Нельсона-Аалена (или процесс Нельсона-Аалена) — это статистический метод для анализа выживаемости, который позволяет оценивать функцию выживаемости и функцию риска смерти на основе наблюдений за выжившими и умершими пациентами.

Применяется он в случае переменного количества событий (например, количество поломок оборудования или количество рецидивов заболевания у пациентов). Метод основан на процессе Пуассона и использует рекурсивное уравнение для вычисления функции выживаемости и функции риска.

Функция выживаемости показывает вероятность того, что пациент не умрет до определенного момента времени. Функция риска смерти показывает вероятность того, что пациент умрет в определенный момент времени, при условии того, что он жив еще в этот момент времени.

Применение метода Нельсона-Аалена позволяет оценить и сравнивать степень риска, с которой пациенты подвержены определенным событиям. Например, исследования на основе метода Нельсона-Аалена могут показать, как соотносятся вероятности рецидива заболевания у пациентов с различными стадиями болезни или с различными лечебными методами.

3. Метод Кокса (Cox regression) основан на предположении о линейной зависимости между логарифмом отношения шансов (отношения вероятностей) и значением объясняющих переменных (факторов). Этот метод применяется для анализа данных выживаемости, когда нам необходимо исследовать влияние различных факторов на вероятность выживания.

Пропорциональность рисков – это основное предположение метода Кокса. Это означает, что отношение шансов для двух групп не зависит от времени наблюдения и остается неизменным во времени. Другими словами, в методе Кокса мы предполагаем, что эффекты факторов на вероятность выживания не меняются со временем.

Для того чтобы выполнить анализ методом Кокса, нужно провести следующие шаги:

1. Собрать данные о вероятности выживания, времени наблюдения и факторах, которые могут оказать влияние на вероятность выживания.
2. Проверить предположение о пропорциональности рисков с помощью графических методов (например, построить кривые Каплан-Майера для каждой группы и проверить, пересекаются ли они).
3. Провести анализ методом Кокса, оценив коэффициенты регрессии и их значимость.
4. Интерпретировать результаты, учитывая предположение о пропорциональности рисков.

Метод Кокса широко используется в медицинском и социальном исследовании для определения влияния факторов на вероятность выживания, например, при оценке эффективности лекарств или прогнозировании выживаемости пациентов.

Заключение

Анализ выживаемости является важным инструментом в медицине, оценке эффективности лечения и многих других областях. Он позволяет оценивать вероятность выживания и выявить факторы, которые могут повлиять на него. Недостатком является то, что анализ выживаемости требует большого количества данных и тщательного их анализа, что может быть очень трудоемким процессом. Однако, при правильном применении, анализ выживаемости может дать ценные результаты и помочь в принятии важных решений.

Напоследок хочу порекомендовать бесплатный вебинар, на котором вы узнаете, какие ключевые сервисы AWS существуют и как их использовать для построения сложной облачной инфраструктуры.

• анализ выживаемости
• анализ данных
• survival analysis

Источник: habr.com