Как посчитать сложность программы

В своей деятельности разработчикам практически ежедневно необходимо разрабатывать алгоритмы различного назначения, которые работают с разным набором данных, начиная от нескольких параметров командной строки, заканчивая таблицами размером в терабайты.

4391 просмотров

Для того чтобы обеспечить эффективную работу с такими данными далеко не всегда достаточно реализовать алгоритм, который первым пришел в голову. Зачастую необходимо провести тщательную оценку выбранного алгоритма и выбранной структуры данных, так как в большинстве случаев перед разработчиком ставится выбор между быстродействием алгоритма и объемом используемой памяти. Для этих целей используется специальный подход, о котором далее будет идти речь.

Говоря о сложности алгоритма принято иметь ввиду O-нотацию. Данная нотация имеет свои корни в мат. анализе. Говорят, что неотрицательная функция f(n) не превосходит по порядку функцию g(n) и пишут O(f(n)) = O(g(n)) , если существует такая натуральная константа C, что f (n)

#16 O(log n) Сложность алгоритма (it-ликбез из тачилы)

Для наглядности разберем простой пример. Допустим, нам на вход поступает массив строк. Наша задача заключается в том, чтобы вместо каждой строчки записать в этот массив длину этой строчки. Если наш массив будет состоять из 5 ячеек, то эта операция будет занимать 5 у. е. времени.

Если же их будет 10, то время будет составлять 10 у. е. Рассуждая таким же способом можно прийти к выводу, что время выполнения нашей задачи линейно зависит от числа элементов этого массива, т. е. от размера входных данных. В таком случае, говорится что время выполнения алгоритма не превосходит O(n), где n – число элементов на входе нашего алгоритма.

На практике далеко не всегда можно также легко и однозначно определить зависимость времени выполнения алгоритма от входных данных. Более того, не совсем удобно учитывать каждое малозначимое ответвление. Поэтому для удобной оценки алгоритмов делается несколько допущений, которые значительно упрощают эту задачу.

Первым таким упрощением является то, что мы можем отбросить константы, которые не являются значительными для сравнения. Например, если у нас есть оценка O(n+5), то она эквивалентна O(n). Однако, если нам требуется сравнить O(3n) и O(2n) мы не можем отбросить эти константы и сказать, что алгоритмы эквивалентны с точки зрения времени выполнения.

Следующим упрощением является тот факт, что мы в праве оставлять только самую большую по степени функцию для оценки времени. Например, при оценке O(n^3+n^2 +4n) мы можем упростить ее до оценки O(n^3). Следующее упрощение связно с асимптотикой. Чаще всего, когда нам важно оценить скорость работы алгоритма речь идет о больших объемах информации.

И здесь нам становится не так важно, поступит ли нам на вход миллион или миллион и одна строка. В таких случаях мы говорим о «худшей» или асимптотической оценке алгоритма. То есть в качестве оценки мы принимаем ту функцию, которая является асимптотой для временной составляющей нашего алгоритма.

Big O notation — всё о сложности алгоритмов

Когда мы говорим о ситуациях, в которых мы заранее уверены в некоторой структуре входных данных или в объемах этих данных, можно говорить об оценке снизу и средней оценке. Оценка снизу означает, что мы рассчитываем время, которое потребует наш алгоритм в случае наиболее удачной структуры данных и наиболее удачного порядка данных в этой структуре. Если же мы говорим о средней оценке, то нам достаточно просто сложить оценки сверху и снизу и разделить их пополам.

Наиболее распространёнными оценками являются линейная O(n), логарифмическая O(logn), степенная O(m^n) и экспоненциальная O(e^n), так как она удобна для перехода к операциям с логарифмами. Как показывает практика комбинаций этих сложностей достаточно чтобы оценить большинство алгоритмов.

Давайте рассмотрим данный подход на примере оценки алгоритмов сортировки. Ниже приведен код самой простой сортировки «пузырьком»

for i in range(N-1): for j in range(N-i-1): if a[j] > a[j+1]: a[j], a[j+1] = a[j+1], a[j]

Здесь мы видим 2 вложенных цикла. Первый цикл верхнего уровня проходится по элементам от 0 до N-1. Вложенный цикл выполняется N-i-1 раз. Итого оба цикла приблизительно займут N*(N-1)/2 операций. Если вспомнить о том, что мы отбрасываем константы и переменные более низкого порядка получим сложность O(N^2).

Теперь посмотрим на более быстрые алгоритмы сортировки, например, сортировку слиянием. Ниже представлен один из вариантов реализации этого алгоритма.

def merge_sort(nums): if len(nums) > 1: mid = len(nums)//2 left = nums[:mid] right = nums[mid:] merge_sort(left) merge_sort(right) i = j = k = 0 while i < len(left) and j < len(right): if left[i] < right[j]: nums[k] = left[i] i+=1 else: nums[k] = right[j] j+=1 k+=1 while i < len(left): nums[k] = left[i] i+=1 k+=1 while j < len(right): nums[k] = right[j] j+=1 k+=1

В данном алгоритме мы сначала получаем дерево разбиения нашего массива, глубина которого равна log(n). Далее для каждого уровня нашего дерева нам нужно пройтись по n элементам, сравнить их и записать промежуточные результаты. Таким образом сложность данного алгоритма n*log(n). Это в свою очередь быстрее чем рассмотренный ранее алгоритм.

Когда мы оценили несколько алгоритмов с точки зрения времени выполнения, мы можем выбрать алгоритм, который работает быстрее всего. Но в процессе реализации такого алгоритма может возникнуть ситуация, когда для корректной работы необходимо создавать специфические структуры данных, а также дублировать некоторые данные.

В этом случае важно оценить, что для нас является более критичным ресурсом — время или память. Чтобы грамотно это оценить необходимо уметь не только выявлять максимальное и минимальное время работы алгоритма, но и оценивать и оптимизировать структуры, в которые мы записываем данные. Приведем пример.

Если для какого-либо алгоритма нам необходимо дублировать целочисленный массив, этот алгоритм может показаться нам недостаточно эффективным, даже если он дает прирост в скорости в 1.2 раза. Однако, если мы проведем тщательный анализ данных, оценим возможные значения этих самых данных можно прийти к выводу, что вместо int64 здесь вполне применим int32 или даже int16, что нивелирует необходимость дупликации данных и позволяет использовать более быстрый алгоритм.

Но может произойти и более сложная ситуация. Допустим наш алгоритм занимается только операциями поиска вставки и удаления. В голову сразу приходит хэш-таблица, которая позволяет делать все эти операции за константное время.

Однако, если мы знаем, что у нас будет не больше 100 элементов нам стоит еще раз подумать о структуре данных, так как операции получения хэша тоже занимают время, а при использовании новых и сложных алгоритмов хэширования, заточенных на избежание коллизий в больших объемах данных это время может быть несоизмеримо больше того времени, которое мы потенциально экономим при использовании этой структуры. Если вернуться к алгоритмам сортировки, рассмотренным ранее, то можно заметить, что сортировка пузырьком работает с исходными данными и не нуждается в дополнительном выделении памяти, тогда как merge sort требует выделение массива такого же размера, как и исходный. Поэтому в данном случае важно понимать какой длины ожидается массив и хватит ли у нас вычислительных ресурсов для его дублирования.

Таким образом, важно помнить, что за двумя зайцами скорее всего угнаться не получится, поэтому важно четко понимать, что для вас обойдется дороже – память или время. А если удалось и ускорить работу алгоритма и использование памяти сократить, лучше на всякий случай перепроверить расчёты.

Источник: vc.ru

Как посчитать сложность программы

Сложность этого действия будет равна:

O ( N ) + O ( N log ⁡ N ) = O ( N + N log ⁡ N ) = O ( N log ⁡ N )

Если мы вызовем функцию f(. ) дважды:

f(. ) f(. )
O ( N ) + O ( N ) = O ( N + N ) = O ( 2 N ) = O ( N )

Константа 2 в вычислениях отбрасывается.

Условия

Отдельно разберем исполнение условий (if). Сначала выполняется само условие, а затем один из блоков (if или else).

if test: block 1 else: block 2

Предположим, что вычисление условия test имеет сложность O(T), блока block 1 – O(B1), а блока block 2 – O(B2).

Тогда сложность всего кода будет равна:

O ( T ) + max ( O ( B 1 ) , O ( B 2 ) )

test выполняется всегда, а один из блоков следом за ним – то есть последовательно. В худшем случае будет выполнен блок с наивысшей сложностью.

Подставим реальные значения:

и вычислим сложность кода:

O ( N ) + max ( O ( N 2 ) , O ( N ) ) =
O ( N ) + O ( N 2 ) = O ( N + N 2 ) = O ( N 2 )

Если бы операция test имела класс сложности O(N 3 ), то общая сложность кода составила бы O(N 3 ).

O ( N 3 ) + max ( O ( N 2 ) , O ( N ) ) =
O ( N 3 ) + O ( N 2 ) = O ( N 3 + N 2 ) = O ( N 3 )

Фактически, общий класс сложности для if-условий можно записать еще проще:

O ( T ) + O ( B 1 ) + O ( B 2 )

Для первого примера в этом случае получим:

O ( N ) + O ( N 2 ) + O ( N ) = O ( N 2 )

В O-нотации мы всегда отбрасываем менее значимые элементы – по сути это аналогично работе функции max . Запись с max лучше отражает суть вычисления, но вы можете выбрать любой удобный для вас вариант.

Закон умножения для O-нотации

O ( f ( n ) ) ∗ O ( g ( n ) ) = O ( f ( n ) ∗ g ( n ) )

Если мы повторяем O(N) раз некоторый процесс с классом сложности O(f(N)), то результирующий класс сложности будет равен:

O ( N ) × O ( f ( N ) ) = O ( N × f ( N ) )

Предположим, некоторая функция f(. ) имеет класс сложности O(N 2 ). Выполним ее в цикле N раз:

for i in range(N): f(. )

Сложность этого кода будет равна:

O ( N ) × O ( N 2 ) = O ( N × N 2 ) = O ( N 3 )

Это правило позволяет вычислять класс сложности для выполнения некоторого повторяющегося несколько раз выражения. Необходимо умножить класс сложности количества повторений на класс сложности самого выражения.

Статический анализ на практике

Возьмем три разные функции, которые решают одну и ту же задачу – определяют, состоит ли список из уникальных значений (не имеет дубликатов). Для каждой функции вычислим класс сложности.

Для всех трех примеров размер списка обозначим как N , а сложность операции сравнения элементов примем за O(1).

Алгоритм 1

Список уникален, если каждое его значение не встречается ни в одном последующем индексе. Для значения alist[i] последующим фрагментом списка будет срез alist[i+1:] .

def is_unique1 (alist : [int]) -> bool: for i in range(len(alist)): # 1 if alist[i] in alist[i+1:]: # 2 return False # 3 return True # 4

Определим сложность для каждой строки метода:

1. O(N) – для каждого индекса. Создание объекта range требует выполнения трех последовательных операций: вычисления аргументов, передачу их в __init__ и выполнение тела __init__ . Две последние имеют класс сложности O(1). Сложность len(alist) также O(1), поэтому общая сложность выражения range(len(alist)) – O(1) + O(1) + O(1) = O(1).
2. O(N) – получение индекса + сложение + создание среза + проверка in: O(1) + O(1) + O(N) + O(N) = O(N)
3. O(1) – в худшем случае никогда не выполняется, можно проигнорировать.
4. O(1) – в худшем случае всегда выполняется.

Таким образом, класс сложности целой функции is_unique1 равен:

O ( N ) × O ( N ) + O ( 1 ) = O ( N 2 )

Если размер списка увеличится вдвое, то выполнение функции займет в 4 раза больше времени.

Возможно, вы хотели написать так:

O ( N ) × ( O ( N ) + O ( 1 ) ) + O ( 1 )

ведь выражение if cостоит из вычисления самого условия (O(N)) и блока return False (O(1)). Но в худшем случае этот блок никогда не будет выполнен и цикл продолжится, поэтому мы не включаем его в формулу. Но даже если добавить его, то ничего не изменится, так как O(N) + O(1) – это по-прежнему O(N).

Кроме того, в худшем случае вычисляемый срез списка – это alist[1:] . Его сложность – O(N-1) = O(N). Однако, когда i == len(alist) этот срез будет пуст. Средний срез содержит N/2 значений, что по-прежнему даем нам сложность O(N).

Вместо срезов можно использовать вложенный цикл. Сложность функции при этом не изменится.

def is_unique1 (alist : [int]) ->bool: for i in range(len(alist)): # O(N) for j in range(i+1, len(alist)): # O(N) if alist[i] == alist[j] # O(1) return False # O(1) return True # O(1)

Класс сложности целой функции тот же:

O ( N ) × O ( N ) × O ( 1 ) + O ( 1 ) = O ( N 2 )

Алгоритм 2

Список уникален, если после его сортировки рядом не находятся одинаковые значения.

Сначала мы копируем список, чтобы не изменять исходную структуру сортировкой – функции обычно не должны влиять на входящие параметры.

def is_unique2 (alist : [int]) -> bool: copy = list(alist) # 1 copy.sort() # 2 for i in range(len(alist)-1): # 3 if copy[i] == copy[i+1]: # 4 return False # 5 return True # 6

Сложность по строчкам:

1. O(N).
2. O(N log N) – для быстрой сортировки.
3. O(N) – на самом деле N-1, но это то же самое. Операции получения размера списка и вычитания имеют сложность O(1).
4. O(1) – сложение, две операции получения элемента по индексу и сравнение – все со сложностью O(1).
5. O(1) – в худшем случае никогда не выполняется.
6. O(1) – в худшем случае всегда выполняется.

Общий класс сложности функции is_unique2 :

O ( N ) + O ( N × log ⁡ N ) + O ( N ) × O ( 1 ) + O ( 1 ) =
O ( N + N log ⁡ N + O ( N × 1 ) + 1 ) =
O ( N + N log ⁡ N + N + 1 ) = O ( N log ⁡ N + 2 N + 1 ) = O ( N log ⁡ N )

Сложность этой реализации меньше, чем is_unique1 . Для больших значений N is_unique2 будет выполняться значительно быстрее.

Наибольшую сложность имеет операция сортировки – она занимает больше всего времени. При удвоении размера списка именно сортировка займет больше половины добавившегося времени выполнения.

Класс сложности O(N log N) хуже, чем O(N), но уже значительно лучше, чем O(N 2 ).

Фактически, в код метода можно внести одно упрощение:

# было copy = list(alist) # O(N) copy.sort() # O(N log N) # стало copy = sorted(alist) # O(N log N)

Функция sorted создает список с теми же значениями и возвращает его отсортированную версию. Поэтому нам не требуется явно создавать копию.

Это изменение ускорит выполнение кода, но не повлияет на его сложность, так как O(N + N log N) = O(N log N). Ускорение – это всегда хорошо, но намного важнее найти алгоритм с минимальной сложностью.

Алгоритм 3

Список уникален, если при превращении в множество (set) его размер не изменяется.

def is_unique3 (alist : [int]) -> bool: aset = set(alist) # O(N) return len(aset) == len(alist) # O(1)

Рассчитать класс сложности для всей функции очень просто:

O ( N ) + O ( 1 ) = O ( N + 1 ) = O ( N )

Таким образом, третья реализация оказалась самой эффективной из всех с линейным временем выполнения. При увеличении размера списка в два раза, время выполнения функции is_unique3 увеличится всего в два раза.

Тело функции можно записать в одну строчку:

return len(set(alist)) == len(alist)

Сложность при этом не изменится.

В отличие от is_unique2 , эта реализация может работать и со смешанными списками (числа и строки). В то же время требуется, чтобы все значения были хешируемыми/неизменяемыми. Например, is_unique3 не будет работать для списка списков.

Одну проблему можно решить разными способами, из которых одни могут быть эффективнее других. Статический анализ (без запуска кода) позволяет оценить сложность выполнения алгоритмов и функций. Это имеет большое значение для работы с большими наборами данных – чем больше размер входных данных, тем больше выигрыш.

В то же время для небольших объемов данных классы сложности неэффективны. Чтобы найти лучший алгоритм в этом случае, необходимо учитывать константы и термины низшего порядка. Также хорошо работает эмпирический, или динамический, анализ.

Кроме того, при анализе важно учитывать дополнительные ограничения реализации (например, типы данных).

Приоритетные очереди

Рассмотрим еще один важный пример зависимости вычислительной сложности от реализации алгоритма – приоритетные очереди.

Этот тип данных поддерживает две операции:

• добавление значения;
• извлечение значения с самым высоким приоритетом из оставшихся.

Разные реализации приоритетных очередей имеют разные классы сложности этих операций:

add	remove
Реализация 1	O(1)	O(N)
Реализация 2	O(N)	O(1)
Реализация 3	O(log N)	O(log N)

Реализация 1

Новое значение добавляется в конец списка (list) или в начала связного списка (linked list) – O(1).

Чтобы найти приоритетное значение для удаления осуществляется поиск по списку – O(N).

Легко добавить, но трудно удалить.

Реализация 2

Для нового значения определяется правильное место – для этого перебираются элементы списка (или связного списка) – O(N).

Зато самое приоритетное значение всегда находится в конце списка (или в начале связного списка) – O(1).

Легко удалить, но трудно добавить.

Реализация 3

Используется двоичная куча, которая позволяет реализовать обе операции со «средней» сложностью O(log N), что для больших значений ближе к O(1), чем к O(N).

Теперь проведем анализ этих реализаций на реальных задачах.

Сортировка

Чтобы отсортировать N значений с помощью приоритетной очереди, нужно сначала добавить все значения в очередь, а затем удалить их все.

Реализация 1

N × O ( 1 ) + N × O ( N ) = O ( N ) + O ( N 2 ) = O ( N 2 )

Реализация 2

N × O ( N ) + N × O ( 1 ) = O ( N 2 ) + O ( N ) = O ( N 2 )

Реализация 3

N × O ( log ⁡ N ) + N × O ( log ⁡ N ) =
O ( N log ⁡ N ) + O ( N log ⁡ N ) = O ( N log ⁡ N )

Примечание: N * O(. ) – это то же самое, что и O(N) * O(. ).

Первая и вторая реализации выполняют одну операцию быстро, а другую медленно. В итоге общий класс сложности определяет самая медленная операция.

Третья реализация оказывается быстрее всех, так как ее среднее время O(N log N) ближе к O(1), чем к O(N).

10 максимальных значений

Теперь найдем с помощью приоритетной очереди 10 максимальных значений. Для этого в очередь помещаются N элементов, а извлекаются только 10.

Реализация 1

N × O ( 1 ) + 10 × O ( N ) = O ( N ) + O ( N ) = O ( N )

Реализация 2

N × O ( N ) + 10 × O ( 1 ) = O ( N 2 ) + O ( 1 ) = O ( N 2 )

Реализация 3

N × O ( log ⁡ N ) + 10 × O ( log ⁡ N ) =
O ( N log ⁡ N ) + O ( log ⁡ N ) = O ( N log ⁡ N )

Теперь первая реализация оказывается самой эффективной, так как операция добавления элемента у нее очень дешевая по времени.

Мораль этого примера заключается в том, что иногда не существует «самой лучшей реализации». В зависимости от задачи оптимальными могут быть разные варианты.

А чтобы найти лучшее решение, важно понимать, что такое вычислительная сложность и как ее определить 🙂

Мне сложно разобраться самостоятельно, что делать?

Алгоритмы и структуры данных действительно непростая тема для самостоятельного изучения: не у кого спросить и что-то уточнить. Поэтому мы запустили курс «Алгоритмы и структуры данных», на котором в формате еженедельных вебинаров вы:

• изучите сленг, на котором говорят все разработчики независимо от языка программирования: язык алгоритмов и структур данных;
• научитесь применять алгоритмы и структуры данных при разработке программ;
• подготовитесь к техническому собеседованию и продвинутой разработке.

Курс подходит как junior, так и middle-разработчикам.

Источники

Источник: proglib.io

Тема 2 Оценка структурной и временной сложности программ Алгоритмическая сложность

Информацию можно записывать разными способами. Иногда удобнее записать «повторить n раз» вместо того, чтобы писать повторяющуюся последовательность одинаковых знаков. Иногда последовательность бывает сложная и невозможно выделить повторяющуюся часть.

Если в качестве объектов будем рассматривать произвольные последовательности символов из некоторого алфавита, то наиболее экономичным способом их описания будет алгоритмический.

Пусть 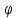— произвольная частично-рекурсивная функция. Тогдамерой сложности последовательности 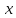назовём величину

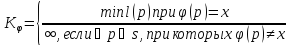
где – программа (код), по которой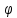восстанавливает последовательность;

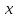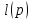
–длина такой программы (количество двоичных разрядов);

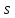
–множество всех допустимых программ;

За меру сложности произвольной последовательности символов из некоторого фиксированного алфавита принимается длина (количество двоичных разрядов) самой короткой программы, генерирующей эту последовательность.

Свойства алгоритмической сложности

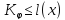
Свойство 1: Сложность последовательности не превосходит её длины.

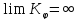
Свойство 2: Сложность последовательности неограниченно растет с увеличением её длины.

Свойство 3: Подавляющее число последовательностей (почти все) несжимаемы, т.е. случайны.

Свойство 4: Функция КY невычисляема, т.е. не существует алгоритма её определения для произвольной символьной последовательности, однако существует общий способ оценки этой величины сверху.

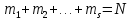
Пусть S – количество символов в алфавите, а N – общее их число в некоторой произвольной последовательности, причем символ с номером l(l = 1, 2, …, s) появляется в ней mi раз:

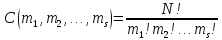
Число всевозможных последовательностей

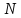
Из свойства 1: Алгоритмическая сложность любой из этих последовательностей не может превосходить количества двоичных разрядов, необходимых для записи их порядковых номеров, иными словами: сложность последовательности не превосходит энтропию произвольной последовательности длины :

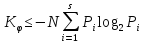
Алгоритмическая сложность любой последовательности не превосходит её энтропии, которую можно найти, определив частоты (вероятности) символов в последовательности

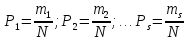
При какой величине алфавита s максимум энтропии H произвольной последовательности из N символов минимален?

Нас интересует минимаксное значение выражения

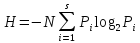
Энтропия 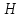имеетмаксимум, когда все символы в последовательности равновероятны.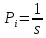

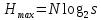
Тогда .

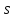не может быть меньше , так как каждый символ алфавита должен появиться в последовательности хотя бы раз. Значит, наименьшее значение энтропии будет.

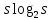Требуется определить значение , при котором приращение энтропии было бы минимально.

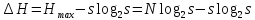
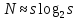
Максимум энтропии минимален при .

Подставляя значение n, получим .

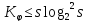
Верхняя оценка уровня алгоритмической сложности:

Метрики структурной сложности программ Понятие структурной сложности программы

Структурная сложность программ определяется:

• Числом взаимодействующих компонентов
• Числом связей между компонентами
• Сложностью взаимодействием компонентов (количество связей)

Разнообразие поведения программы и связей между её входными и результирующими данными определяется набором маршрутов (чередующихся последовательностей вершин и дуг графа управления), по которым выполняется программа. Сложность программного модуля связана не столько с размером (числом команд) программы, сколько с числом маршрутов её исполнения и сложностью. Маршруты возможной обработки данных определяют сложность разработки программы. Данную метрику сложности можно использовать для оценки трудоёмкости тестирования и сопровождения модуля, а также для оценки потенциальной надежности его функционирования. Маршруты исполнения программного модуля подразделяются на:

• Вычислительные маршруты
• Маршруты принятия логических решений

Сложность вычисления маршрутов оценивается формулой: 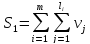m – количество маршрутов выполнения программы, 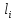–число данных, обрабатываемых в i-ом маршруте 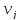–число значений, обрабатываемых данных j-ого типа (2 ≤ 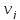≤ 5) Общее количество арифметических операций не выходит за пределы 5-10%, поэтому вычислительные маршруты определяют структурную сложность программы. Сложность маршрутов принятия логических решений оценивается формулой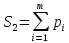 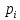–число ветвлений или число проверяемых условий в i-ом маршруте. Общая сложность программы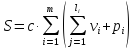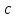–коэффициент пропорциональности.

Источник: studfile.net