Построение корреляционных таблиц, как отмечалось выше, один из методов выявления наличия корреляционной зависимости. Поскольку выполнение лабораторной работы предусматривает ее построение, рассмотрим пример построения корреляционной таблицы с использованием некоторых вспомогательных модулей ППП STATISTICA.
Корреляционная таблица – это результат группировки единиц изучаемой совокупности по двум признакам: в подлежащем таблицы выделяются группы по факторному признаку х, в сказуемом – по результативному у или наоборот. В клетках таблицы на пересечении x и у подсчитывается число случаев совпадения каждого значения х с соответствующим значением у (частоты). Общий вид такой таблицы показан на условном распределении 40 единиц (Таблица 7.1). Здесь в качестве х может рассматриваться, например, стаж работы (число лет), а в качестве у – производительность труда, n = 40 – число рабочих.
Пример корреляционной таблицы
| Значение признака xj | Значение признака yi | Итого (число единиц) fx = fj | Среднее значение по группам |
| — | — | 8,75 | |
| — | 12,08 | ||
| — | 15,31 | ||
| — | — | 16,87 | |
| Итого (число единиц) fy = fi | ∑f = 40 | 14,0 |
В первой строке значению факторного признака х =1 один раз соответствует значение у = 5 и три раза у = 10. Аналогично во второй строке, где х = 3, два раза этому значению соответствует у = 5, три раза у = 10 и семь раз у =15 и т.д.
Расчет коэффициента корреляции в Excel
В итоговой строке имеем распределение всех 40 единиц совокупности по результативному признаку у (частоты обозначены fy). В итоговом столбце — распределение тех же 40 единиц, но по признаку фактору х (обозначение частот fx). В последней графе рассчитывается среднее значение признака-результата, то есть :
Например, для первой строки:
Эти значения могут быть использованы для построения эмпирической линий регрессии для и .
Как видно их таблицы, по мере увеличения значений х групповые средние значений тоже увеличиваются от группы к группе, что позволяет сделать вывод о том, что между признаками существует прямая корреляционная зависимость.
О наличии и направлении связи можно судить и по «внешнему виду» таблицы, т.е. по расположению в ней частот.
Так, если частоты разбросаны в клетках таблицы беспорядочно, то это чаще всего свидетельствует либо об отсутствии связи между группировочными признаками, либо об их незначительной зависимости.
Если же частоты сконцентрированы ближе к одной из диагоналей таблицы, образуя своего рода эллипс, то это почти всегда свидетельствует о наличие зависимости, близкой к линейной. Расположение по диагонали из верхнего левого угла в нижний правый свидетельствует о прямой линейной зависимости между показателями, наоборот – об обратной.
Рассмотрим конкретный пример. Менеджер по маркетингу в компании, владеющей сетью супермаркетов, желает оценить влияет ли расстояние между полками на объем продаж корма для домашних животных. Для анализа сформирована случайная выборка из 12 магазинов.
КОРРЕЛЯЦИЯ Спирмена Пирсона STATISTICA #08
Соотношение расстояний между полками в сети супермаркетов и
еженедельным объемом продаж
| Магазин | Расстояние между полками, Х (метры) | Еженедельный объем продаж, Y (тыс.долл.) |
| 1,52 | 0,16 | |
| 1,52 | 0,22 | |
| 1,52 | 0,14 | |
| 3,05 | 0,19 | |
| 3,05 | 0,24 | |
| 3,05 | 0,26 | |
| 4,57 | 0,23 | |
| 4,57 | 0,27 | |
| 4,57 | 0,28 | |
| 6,10 | 0,26 | |
| 6,10 | 0,29 | |
| 6,10 | 0,31 |
Для определения числа интервалов и величины интервала для построения корреляционной таблицы можно воспользоваться меню Statistics/Basic Statistics/Tables (рис. 7.1.)
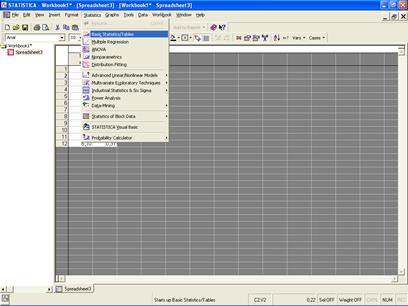
Рис. 7.1. Выбор меню Basic Statistics/Tables в ППП STATISTICA.
В появившемся окне выбираем пункт Frequency tables.
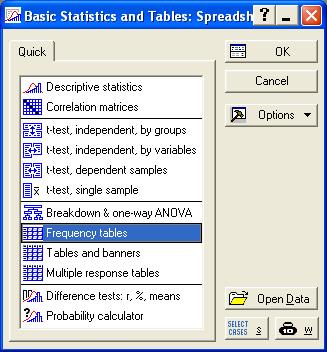
Рис. 7.2. Выбор меню Frequency tables.
С помощью кнопки Variables выбираем переменную, соответствующую зависимой (результативной) переменной, то есть у; переходим на закладку Advanced, на которой задаем необходимые опции построения таблицы частот. Напомним, что необходимо воспользоваться закладкой Options и убрать метку с поля Count and report missing data (MD), чтобы исключить подсчет незаполненных ячеек (рис. 7.3., 7.4.).
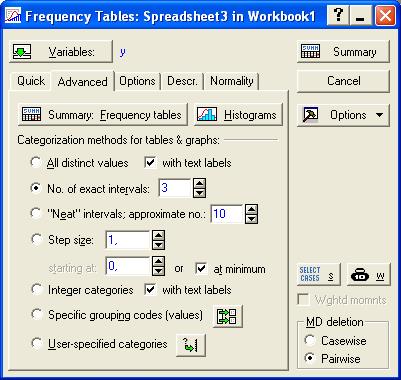
Рис. 7.3. Вид закладки Advanced функции Frequency tables.
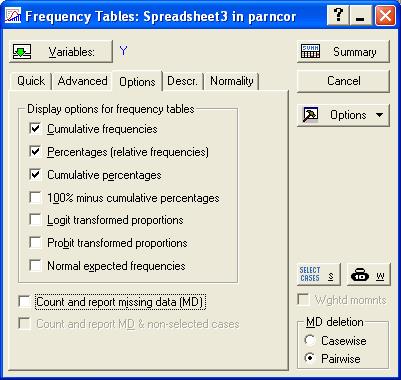
Рис. 7.4. Вид закладки Options функции Frequency tables.
Требования, предъявляемые к построению таблиц частот, а также подробное описание данного меню и описание содержания таблицы можно найти в первой части учебного пособия по статистике, посвященной анализу распределений.

Рис. 7.5. Распределение еженедельного объема продаж кормов для животных в супермаркетах с числом интервалов к = 3.
В данном примере подобрано число интервалов равное трем. При этом можно воспользоваться результатами, предложенными системой, как для определения числа интервалов, так и для определения величины интервала.
Возможен второй вариант – расчет величины интервала вручную:
, (7.2)
где R – размах вариации,
k – число интервалов.
В рамках данной работы строится корреляционная таблица с нанесенными на нее линиями регрессии х и у (рис. 7.6.). В первой строке представлены границы интервалов группировки результативного признака, в правом столбце – факторного. В левом столбце частоты факторного признака, в нижней строке — результативного.
Во второй строке и в столбце, предшествующем правому приведены середины интервалов, используемые для расчета точек линии регрессии. В самой таблице звездочками отмечены координаты точек по двум показателям (попарно).
Далее рассчитываются средние значения признака-результата и признака-фактора в каждой группе. Они же являются точками линий регрессии. Точки эмпирической линии регрессии наносятся в масштабе квадратов таблицы, соответственно оси признака. Ниже приведены примеры расчета координат нескольких точек:
Источник: studopedia.su
Корреляционный анализ
Вопросы описания порядка проведения корреляционного анализа в «STATGRAPHICS» представлены в учебном пособии [2].
Для обнаружения связи между переменными, исследования ее силы, направленности служит совокупность методов, называемая корреляционным анализом, в рамках которого оцениваются и анализируются различные показатели связи и их значимость. Цель показателя (меры) связи состоит в том, чтобы дать простой численный ответ на вопрос о степени корреляционной зависимости между двумя переменными. Для изучения связи между двумя признаками номинального типа применяются таблицы сопряженности, статистика Фишера-Пирсона χ 2 , различные меры связи признаков (коэффициенты Крамера, Юля, Чупрова и др.).
Для признаков, измеренных в порядковой шкале, при исследовании связи применяются коэффициенты корреляции рангов, например Спирмена или Кендола.
При исследовании связи двух количественных переменных применяются коэффициенты корреляции, корреляционное отклонение, коэффициенты корреляции рангов. Коэффициент корреляции нашел широкое применение в практике, но важно помнить, что он характеризует линейную форму связи (в отличие от корреляционного отклонения). Для качественных признаков и количественных данных, которые не показывают «нормального» распределения, корректным является использовать коэффициент корреляции рангов.
В «STATGRAPHICS» расчет коэффициентов корреляции реализован в пункте главного меню DiscribleNumeric DatаMulti-Variable Analysis, при выборе которого появляется стандартный диалог для определения анализируемых данных. В строке «Data» можно задать две и более переменных, между которыми необходимо оценить показатели связи. В окне результата первоначально выводится список анализируемых переменных и объем многомерной выборки. Для расчета коэффициентов корреляции необходимо активировать опцию — «Tаbular Options», а в появившемся окне (рисунок 17) выбрать пункты «Correlations» иили «Rank Correlations».
При этом нужно помнить о типе анализируемых данных и корректно выбрать оцениваемые показатели связи, а также интерпретировать получаемые результаты.
Результаты оценки коэффициентов корреляции будут представлены в виде корреляционных матриц (рисунок 18).
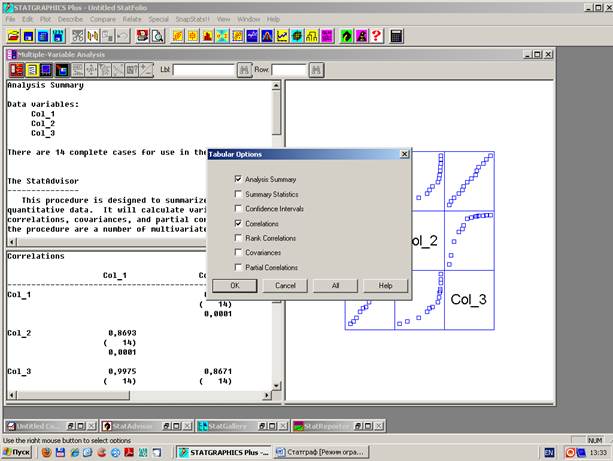
Рисунок 17 – Окно выбора параметров корреляционного анализа
Для каждой пары переменных выводятся три значения. Первое – это оценка коэффициента корреляции. Второе значение – объем выборки. Третье значение – это достигаемый уровень значимости (p-value) полученной оценки коэффициента корреляции. Если p-value меньше 0,05, то это говорит о наличии статистически значимой ненулевой корреляции между этими двумя переменными с 95 %-й надежностью.

Рисунок 18 – Окно оценки корреляционной матрицы
Контрольные вопросы
1 Какие есть возможности программы для статистического анализа?
2 Как выбрать переменную для статистического анализа?
3 Как происходит отбор данных?
4 Правила выбора опций статистического анализа.
5 Как происходит группировка данных?
Регрессионный анализ
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник: studopedia.ru
2 способа корреляционного анализа в Microsoft Excel

Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.
Суть корреляционного анализа
Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.
Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго.
При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.
Расчет коэффициента корреляции
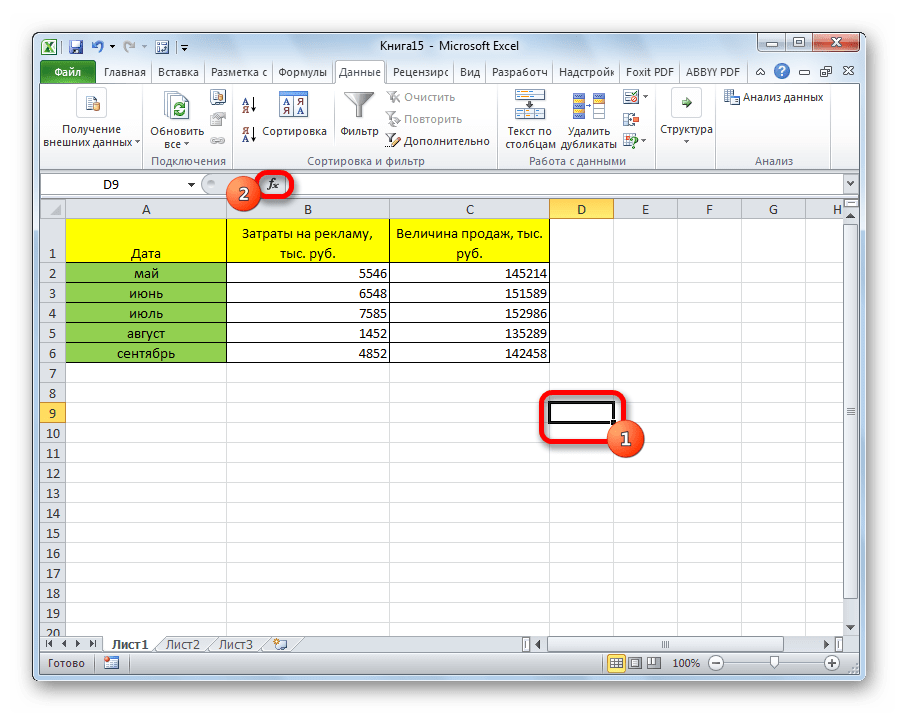
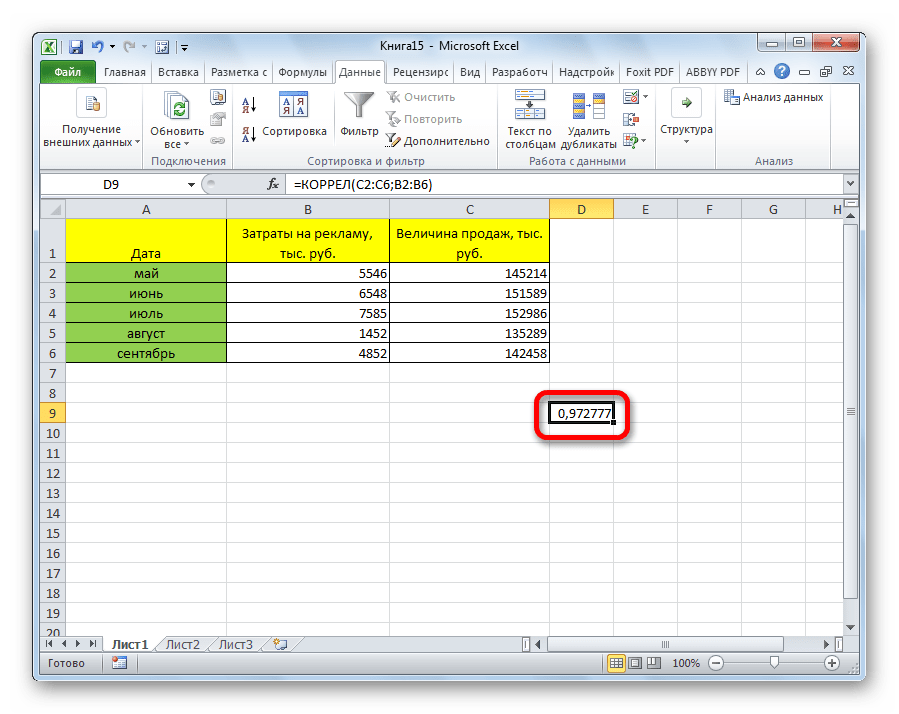
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.
Способ 1: определение корреляции через Мастер функций
Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).
-
Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
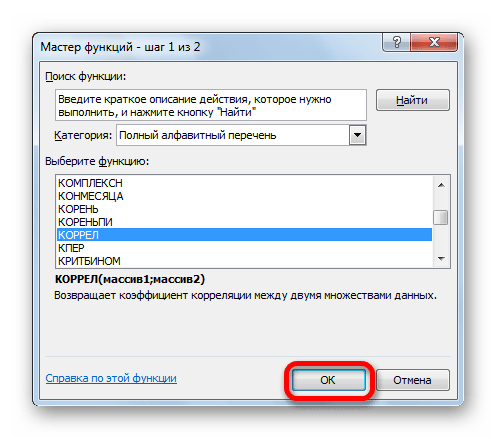
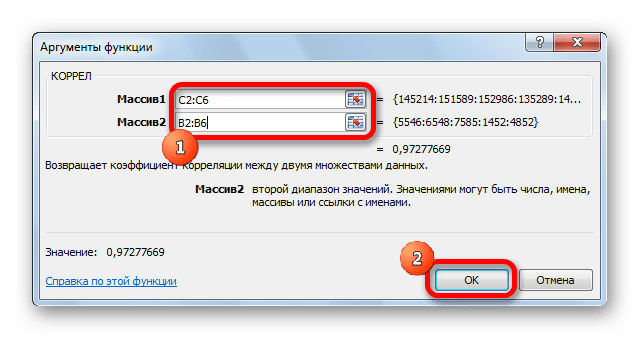
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.
Способ 2: вычисление корреляции с помощью пакета анализа
Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.
- Переходим во вкладку «Файл».
- В открывшемся окне перемещаемся в раздел «Параметры».
- Далее переходим в пункт «Надстройки».

- В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».

- В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
- После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
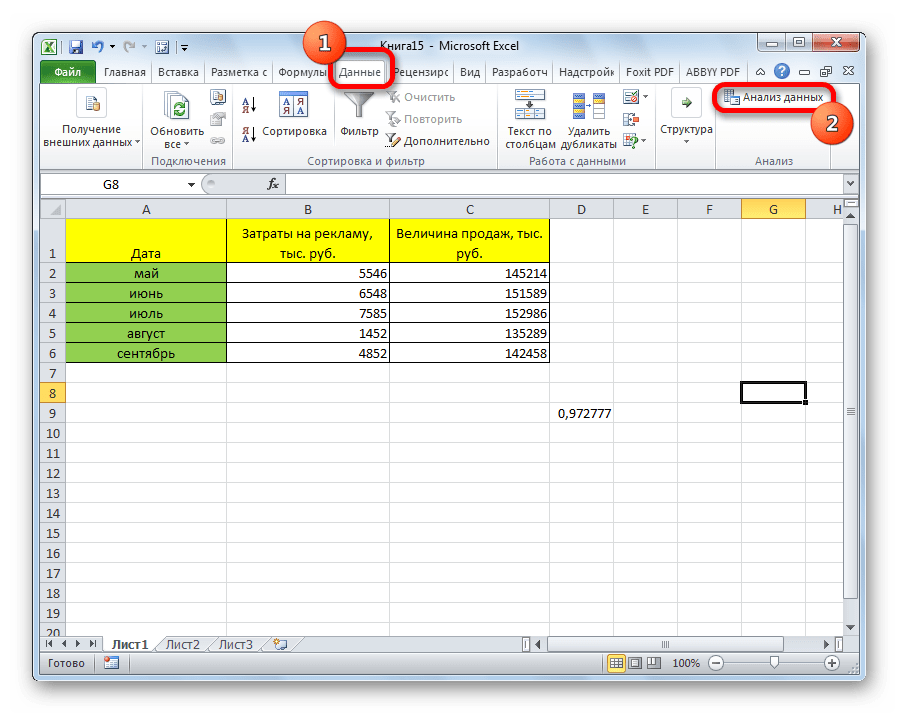
- Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
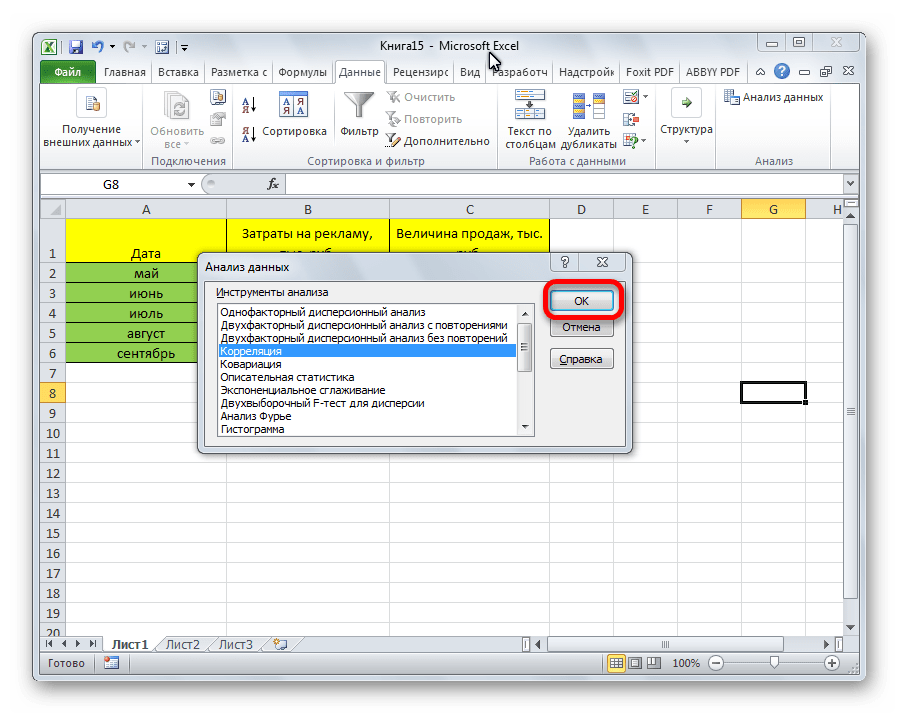
- Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж». Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам». В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл). Когда все настройки установлены, жмем на кнопку «OK».
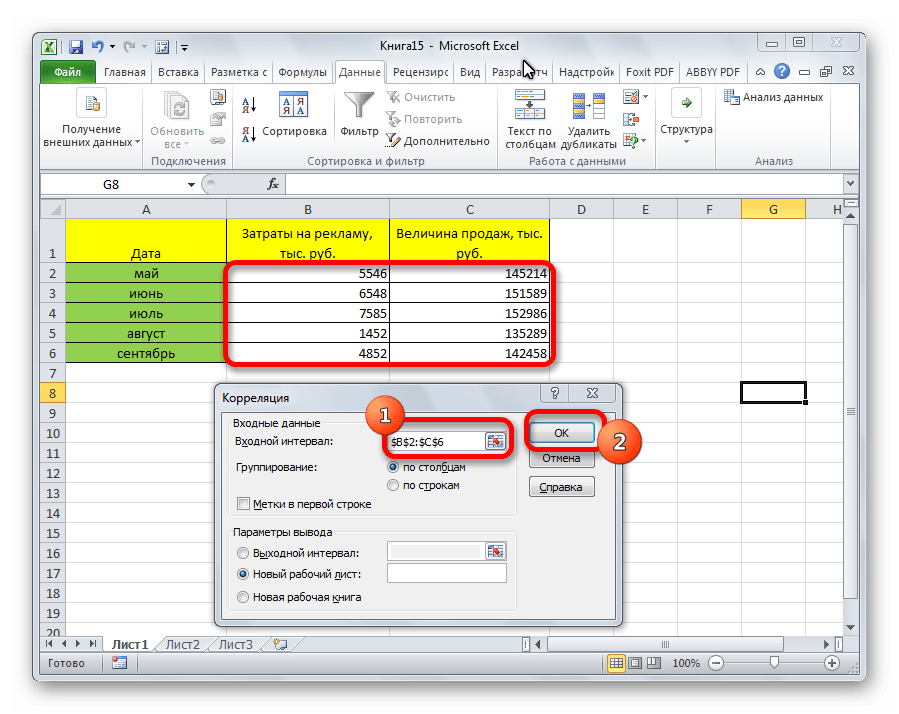
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.
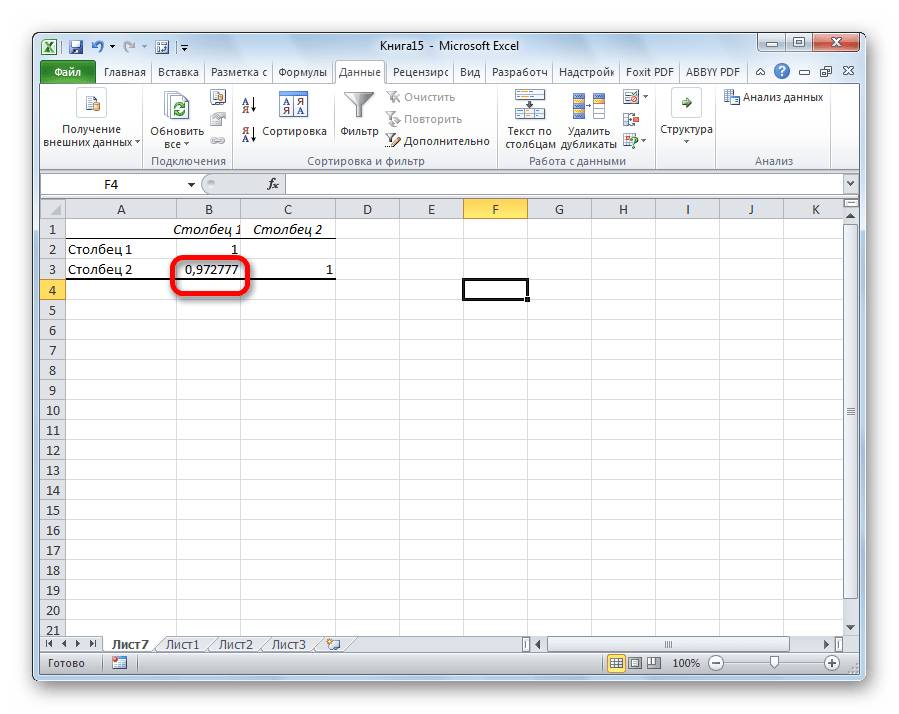
Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.
Источник: lumpics.ru