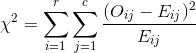
Критерий независимости Хи-квадрат используется для определения того, существует ли значительная связь между двумя категориальными переменными.
В этом руководстве объясняется, как выполнить тест независимости хи-квадрат в Stata.
Пример: критерий независимости хи-квадрат в Stata
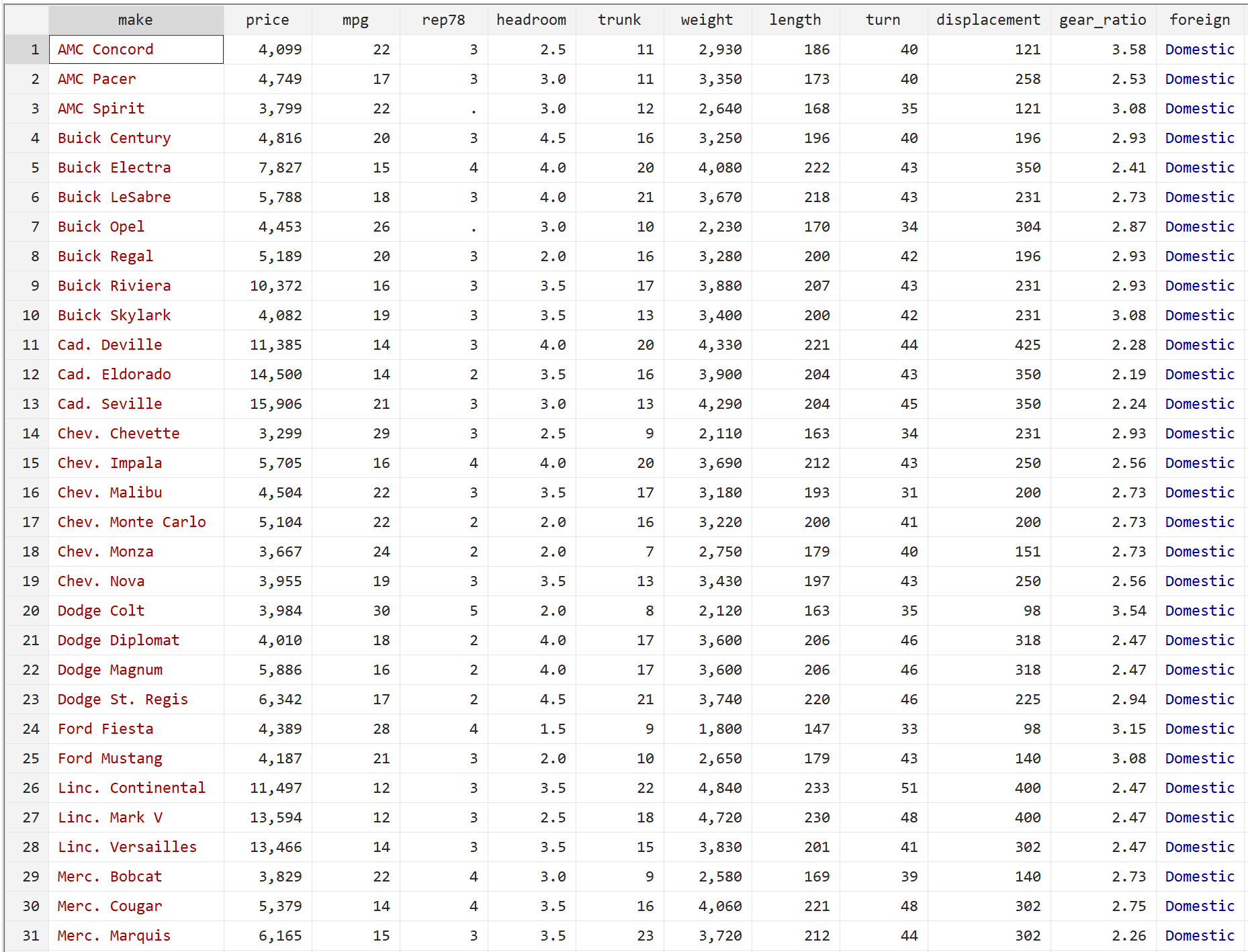
В этом примере мы будем использовать набор данных auto , который содержит информацию о 74 различных автомобилях 1978 года.
Используйте следующие шаги, чтобы выполнить критерий независимости хи-квадрат, чтобы определить, существует ли значительная связь между следующими двумя переменными:
- rep78: сколько раз машина ремонтировалась в 1978 году (от 1 до 5)
- иностранный: является ли тип автомобиля иностранным (0 = нет, 1 = да)
Шаг 1: Загрузите и просмотрите необработанные данные.
Сначала мы загрузим данные, введя следующую команду:
Теория вероятностей #17: критерий хи квадрат (Пирсона)
сисус авто
Описание непараметрических процедур на примерах

Опция открывает диалоговое окно, в котором можно ввести частоты в таблицу 2×2 (состоящую из двух строк и двух столбцов) и вычислить различные статистики, позволяющие оценить зависимость между двумя переменными, принимающими только два значения.
| Пепси | Кола | Сумма |
| Мужчины | ||
| Женщины | ||
| Сумма |

Типичный пример таких таблиц — определение, например, числа мужчин и женщин, предпочитающих рекламу ПЕПСИ или КОКИ, или числа заболевших и не заболевших людей из числа сделавших и не сделавших прививки, и т. д.
Итак, одна переменная — ПОЛ, другая переменная — НАПИТОК. Первая переменная имеет 2 уровня (принимает 2 значения) — мужчина, женщина. Вторая переменная, НАПИТОК, также имеет 2 уровня, например, ПЕПСИ или КОКА.
Задача состоит в том, чтобы оценить зависимость между двумя табулированными переменными.
Укажем на важное методологическое отличие использования слова связь (зависимость) в повседневной жизни и в анализе данных. Обычно мы говорим, что два признака А и В связаны между собой, если они часто встречаются вместе. В анализе данных дается строгое определение: если А встречается относительно чаще с В, чем с не-В, то А и В связаны. Или переходя на язык теории вероятностей, Р(АХВ) должна быть больше Р(АХ не-В). Оценкой вероятности является частота.
В приведенной выше таблице пусть признак А — пол, признак В — напиток, принимающий, например, два значения: пепси — не-пепси. Пусть a, b — частоты в первой строке, с, d — частот во второй строке. Если а/(а+с) = b/(b+d) то признаки независимы. Формально имеем: 17/(17+27) = 0,39, 19/(19+29) — 0,396. Теперь нам нужно понять, существенно или нет различие в частотах.
Хи квадрат ПИРСОНА STATISTICA #07
Статистические критерии, реализованные в этом диалоге, как раз и позволяют это сделать. В данном случае различие, конечно, несущественно (или, как говорят в анализе данных, незначимо). Следовательно, признаки независимы, — пол не связан с выбором напитка.
Опция 2×2 может быть использована как альтернатива корреляциям, если обе рассматриваемые переменные являются категориальными.
Дополнительно к стандартному критерию хи-квадрат Пирсона и скорректированному хи-квадрат вычисляются следующие статистики:

Классическая статистика хи-квадрат Пирсона замечательна тем, что ее распределение приближается распределением хи-квадрат, для которого имеются подробные таблицы. Процентные точки распределения хи-квадрат могут быть также эффективно вычислены в системе STATISTICA с помощью вероятностного калькулятора.
Свойство критерия хи-квадрат (точность аппроксимации распределения статистики распределением хи-квадрат) для таблиц 2× 2 с малыми ожидаемыми частотами может быть улучшено за счет уменьшения абсолютного значения разностей между ожидаемыми и наблюдаемыми частотами на величину 0,5 перед возведением в квадрат.
Это так называемая поправка Йетса на непрерывность для таблиц частот 2×2, которая обычно применяется, когда ячейки содержат только малые частоты и некоторые ожидаемые частоты становятся меньше 5 (или даже меньше 10).
Хи-коэффициент. Статистика хи-квадрат представляет собой меру связи между номинальными или категориальными переменными, значения которых нельзя упорядочить.
Пусть даны частоты в таблице 2×2. Предположим, что оба фактора в таблице независимы. Зададимся вопросом: какова вероятность получить наблюдаемые частоты? Это и делается в критерии Фишера. STATISTICA вычисляет р-уровни одностороннего и двустороннего критерия Фишера.
Если сумма частот небольшая, то лучше использовать точный критерий Фишера вместо критерия хи-квадрат.
Известны рекомендации Кокрена для таблиц 2×2: если сумма всех частот в таблице меньше 20, то следует использовать точный критерий Фишера.
Если сумма частот больше 40, то можно применять критерий хи-квадрат с поправкой на непрерывность.
Рассмотрим следующий пример.
Пример. Исследуются 30 человек, совершивших преступления. У каждого из преступников есть брат-близнец. Спрашивается, имеется ли связь между родственными отношениями и преступлением. Данные приведены в таблице:
| Оба брата преступники | Только один брат преступник | Сумма |
| Однояйцевые близнецы | ||
| Разнояйцовые близнецы | ||
| Сумма |
Проверяемая гипотеза состоит в том, что зависимости между родством и преступностью нет. Альтернативная гипотеза заключается в следующем: чем теснее родственные связи, тем более вероятно совместное участие в преступлении (то есть между признаками имеется положительная связь). Заметьте — это односторонняя альтернатива, т. к. нас интересует отклонение от гипотезы лишь в одну сторону (вольно выражаясь, с сохранением знака больше).
Введем данные в систему STATISTICА.

После нажатия на кнопку ОК получим следующую электронную таблицу с результатами:

Так как в данных имеются ячейки с малыми частотами (2 и 3), то для улучшения точности критерия хи-квадрат используем поправку Йетса. Поскольку нас интересует односторонняя альтернатива, мы делим уровень р = 0,0012 пополам и получаем 0,0006.
Точное значение одностороннего критерия Фишера равно 0,0005 (см. таблицу). Оба эти результата высокозначимы, следовательно, мы отвергаем исходную гипотезу об отсутствии зависимости между родством и преступлением в пользу альтернативы: «между признаками имеется тесная положительная связь».
Заметьте, что сумма всех частот в таблице меньше 40, но оба критерия, точный Фишера и хи-квадрат Йетса, дают почти одинаковые результаты.
Критерий хи-квадрат Макнемара. Этот критерий применяется, когда частоты в таблице 2×2 получены по зависимым выборкам. Например, когда наблюдения фиксируются до и после воздействия на одном и том же экспериментальном материале.
STATISTICА включает также модуль Логлинейный анализ, позволяющий выполнить полный логлинейный анализ многовходовых таблиц сопряженности. STATISTICA содержит программу на STATISTICA BASIC для вычисления критерия Ментела—Хенцела (файл Ma.nthaen.stb в каталоге STBASIC), позволяющего сравнить две группы данных. Обратитесь к комментариям в программе Manthaen.stb за дополнительной информацией.
Источник: poisk-ru.ru
КРИТЕРИЙ ХИ-КВАДРАТ ПИРСОНА

– это непараметрический метод, который позволяет оценить значимость различий между фактическим (выявленным в результате исследования) количеством исходов или качественных характеристик выборки, попадающих в каждую категорию, и теоретическим количеством, которое можно ожидать в изучаемых группах при справедливости нулевой гипотезы. Выражаясь проще, метод позволяет оценить статистическую значимость различий двух или нескольких относительных показателей (частот, долей).
1. История разработки критерия χ 2
Критерий хи-квадрат для анализа таблиц сопряженности был разработан и предложен в 1900 году английским математиком, статистиком, биологом и философом, основателем математической статистики и одним из основоположников биометрики Карлом Пирсоном (1857-1936).
2. Для чего используется критерий χ 2 Пирсона?
Критерий хи-квадрат может применяться при анализе таблиц сопряженности, содержащих сведения о частоте исходов в зависимости от наличия фактора риска. Например, четырехпольная таблица сопряженности выглядит следующим образом:
| Исход есть (1) | Исхода нет (0) | Всего | |
| Фактор риска есть (1) | A | B | A + B |
| Фактор риска отсутствует (0) | C | D | C + D |
| Всего | A + C | B + D | A + B + C + D |
Как заполнить такую таблицу сопряженности? Рассмотрим небольшой пример.
Проводится исследование влияния курения на риск развития артериальной гипертонии. Для этого были отобраны две группы исследуемых — в первую вошли 70 человек, ежедневно выкуривающих не менее 1 пачки сигарет, во вторую — 80 некурящих такого же возраста. В первой группе у 40 человек отмечалось повышенное артериальное давление. Во второй — артериальная гипертония наблюдалась у 32 человек. Соответственно, нормальное артериальное давление в группе курильщиков было у 30 человек (70 — 40 = 30) а в группе некурящих — у 48 (80 — 32 = 48).
Заполняем исходными данными четырехпольную таблицу сопряженности:
| Артериальная гипертония есть (1) | Артериальной гипертонии нет (0) | Всего | |
| Курящие (1) | 40 | 30 | 70 |
| Некурящие (0) | 32 | 48 | 80 |
| Всего | 72 | 78 | 150 |
В полученной таблице сопряженности каждая строчка соответствует определенной группе исследуемых. Столбцы — показывают число лиц с артериальной гипертонией или с нормальным артериальным давлением.
Задача, которая ставится перед исследователем: имеются ли статистически значимые различия между частотой лиц с артериальным давлением среди курящих и некурящих? Ответить на этот вопрос можно, рассчитав критерий хи-квадрат Пирсона и сравнив получившееся значение с критическим.
3. Условия и ограничения применения критерия хи-квадрат Пирсона
- Сопоставляемые показатели должны быть измерены в номинальной шкале (например, пол пациента — мужской или женский) или в порядковой (например, степень артериальной гипертензии, принимающая значения от 0 до 3).
- Данный метод позволяет проводить анализ не только четырехпольных таблиц, когда и фактор, и исход являются бинарными переменными, то есть имеют только два возможных значения (например, мужской или женский пол, наличие или отсутствие определенного заболевания в анамнезе. ). Критерий хи-квадрат Пирсона может применяться и в случае анализа многопольных таблиц, когда фактор и (или) исход принимают три и более значений.
- Сопоставляемые группы должны быть независимыми, то есть критерий хи-квадрат не должен применяться при сравнении наблюдений «до-«после». В этих случаях проводится тест Мак-Немара (при сравнении двух связанных совокупностей) или рассчитывается Q-критерий Кохрена (в случае сравнения трех и более групп).
- При анализе четырехпольных таблиц ожидаемые значения в каждой из ячеек должны быть не менее 10. В том случае, если хотя бы в одной ячейке ожидаемое явление принимает значение меньше 10, то для анализа лучше использовать точный критерий Фишера.
- В случае анализа многопольных таблиц ожидаемое число наблюдений не должно принимать значения менее 5 более чем в 20% ячеек. В случае несоблюдения данного условия для сравнения долей следует также использовать точный критерий Фишера.
4. Как рассчитать критерий хи-квадрат Пирсона?
- Рассчитываем ожидаемое количество наблюдений для каждой из ячеек таблицы сопряженности (при условии справедливости нулевой гипотезы об отсутствии взаимосвязи) путем перемножения сумм рядов и столбцов с последующим делением полученного произведения на общее число наблюдений. Общий вид таблицы ожидаемых значений представлен ниже:
| Исход есть (1) | Исхода нет (0) | Всего | |
| Фактор риска есть (1) | (A+B)*(A+C) / (A+B+C+D) | (A+B)*(B+D)/ (A+B+C+D) | A + B |
| Фактор риска отсутствует (0) | (C+D)*(A+C)/ (A+B+C+D) | (C+D)*(B+D)/ (A+B+C+D) | C + D |
| Всего | A + C | B + D | A+B+C+D |