Дисперсия — это способ измерения разброса значений в наборе данных.
Формула для расчета дисперсии населения :
σ 2 = Σ (xi – μ) 2 / N
- Σ : символ, означающий «сумма».
- μ : Среднее значение населения
- x i : i -й элемент из совокупности
- N : Численность населения
Формула для расчета выборочной дисперсии :
s 2 = Σ (x i – x ) 2 / (n-1)
Лабораторная работа 7 однофакторный дисперсионный анализ в ппп “statistica”
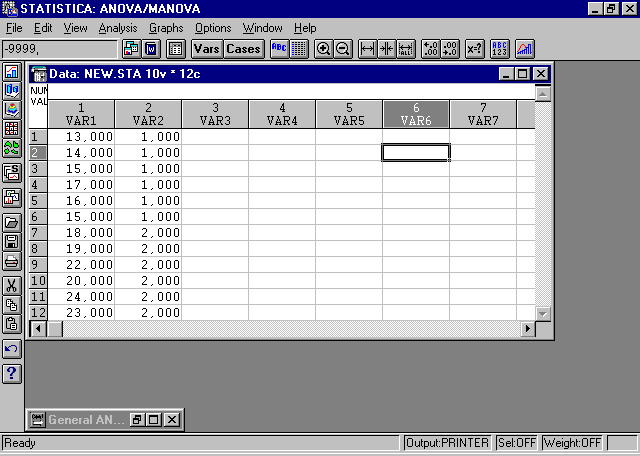
Р исунок 1 – Массив исходных данных для однофакторного дисперсионного анализа.
- В верхней командной строке выбираем Analysis / Resume Analysis, появляется меню ANOVA/ MANOVA.
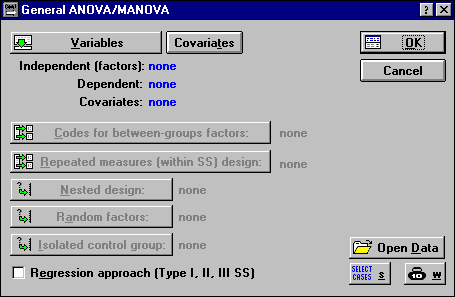
Рисунок 2 – Меню дисперсионного анализа.
Выбираем переменные, нажимая кнопку “Variables”, появляется диалоговое окно, в котором задаем зависимую – Dependent variable (в нашем случае это VAR 1) и независимую – Independent variable переменные (Рисунок 3).
Математическое Ожидание, Дисперсия, Стандартное Отклонение за 5 минут
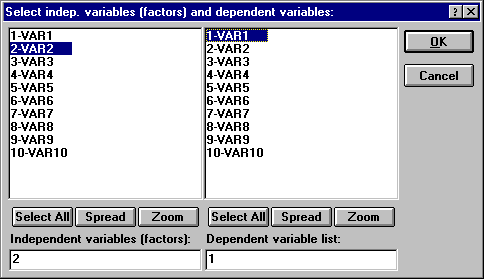
Рисунок 3 – Выбор переменных.
После выбора переменных нажимаем ОК, появляется диалоговое окно General ANOVA / MANOVA, нажимаем ОК. На мониторе появляются предварительные результаты и опции дисперсионного анализа (Рисунок 4).
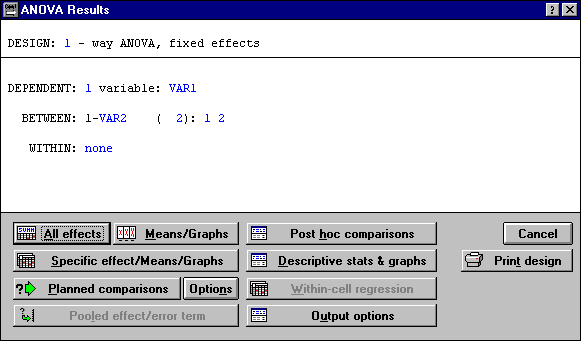
Рисунок 4 – Предварительные результаты
Из опций, представленных на рисунке 4, выбираем Specific effect (Means) Graphs. Результат дисперсионного анализа на рисунке 5.
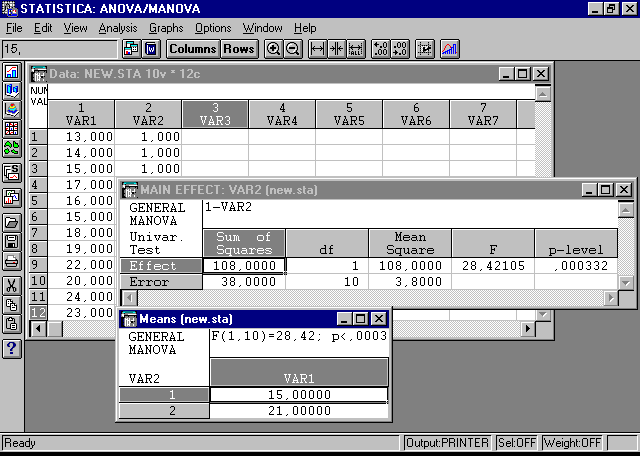
Рисунок 5 – Результат дисперсионного анализа
Лабораторная работа 8 дисперсионный анализ в ms excel
1 Однофакторный дисперсионный анализ
Правление фирмы решает изучить результаты продвижения на книжный рынок научной литературы, надеясь извлечь из них информацию, которой можно было бы воспользоваться при организации и проведении компании по распространению новых изданий.
С этой целью была выделена контрольная группа продавцов, не имеющих опыта работы. Вторая группа имела стаж работы 1-3 года. Третью группу составляли работники со стажем более 3-х лет.
Чтобы обеспечить по всем трем вариантам выровненные условия, были сформированы пять групп, приблизительно равноценных по показателям. Каждая группа включала 3 человека. Результаты работы приведены в таблице 19.
Таблица 19 — Количество проданной научной литературы, шт. (в среднем за месяц)
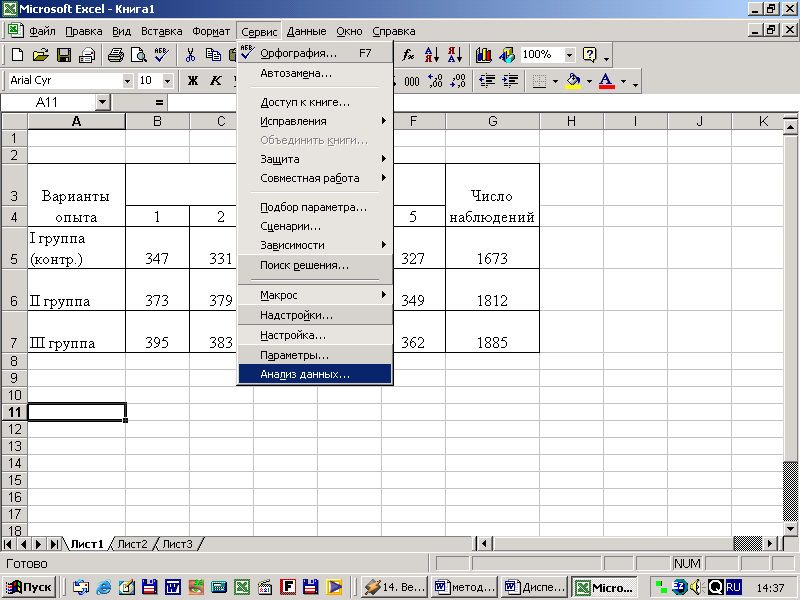
В меню «Сервис» выбираем команду «Анализ данных» (рисунок 6)
Элементы статистики. Дисперсия. Стандартное отклонение
Рисунок 6 Выбор пакета «Анализ данных»
После выполнения команды «Анализ данных» на экране появится список инструментов статистического анализа (рисунок 7), в этом списке находим строку «Однофакторный дисперсионный анализ», нажимаем клавишу «Enter», после этого на экране появится диалоговое окно (рисунок 8).
Здесь требуется указать: входной интервал, способ группирования, выходной интервал.
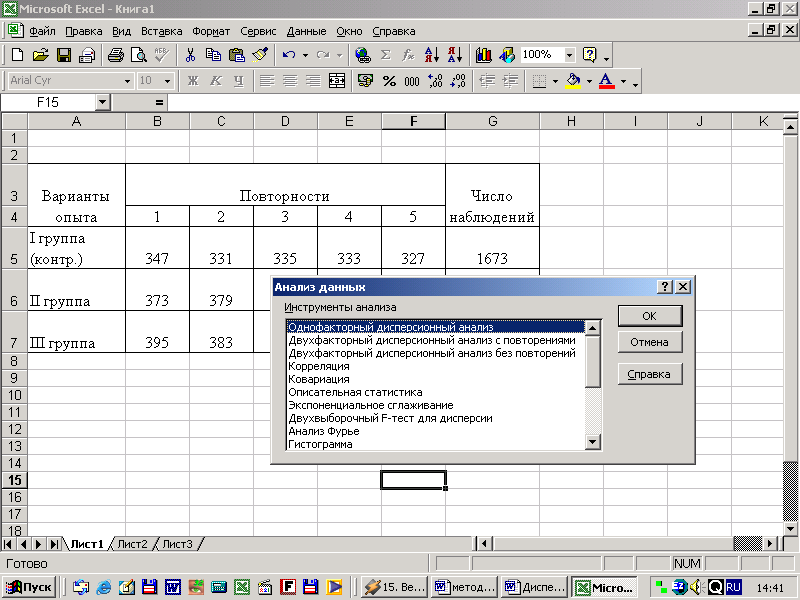
Рисунок 7 — Список инструментов статистического анализа.
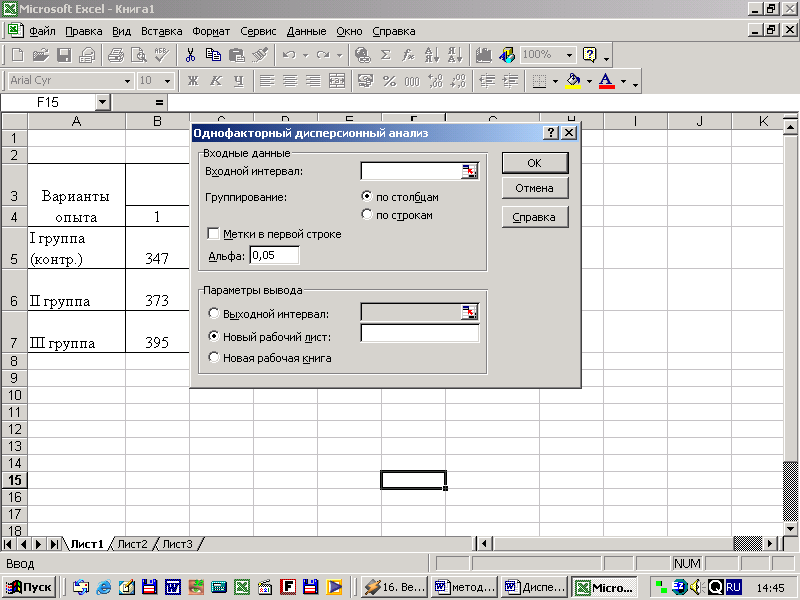
Рисунок 8 — Диалоговое окно «Однофакторный дисперсионный анализ».
Входной диапазон – это ссылка на ячейки, содержащие анализируемые данные. Ссылка должна состоять как минимум из двух смежных диапазонов данных, организованных в виде столбцов или строк. Входной интервал можно задать при помощи мыши , или набрать на клавиатуре.
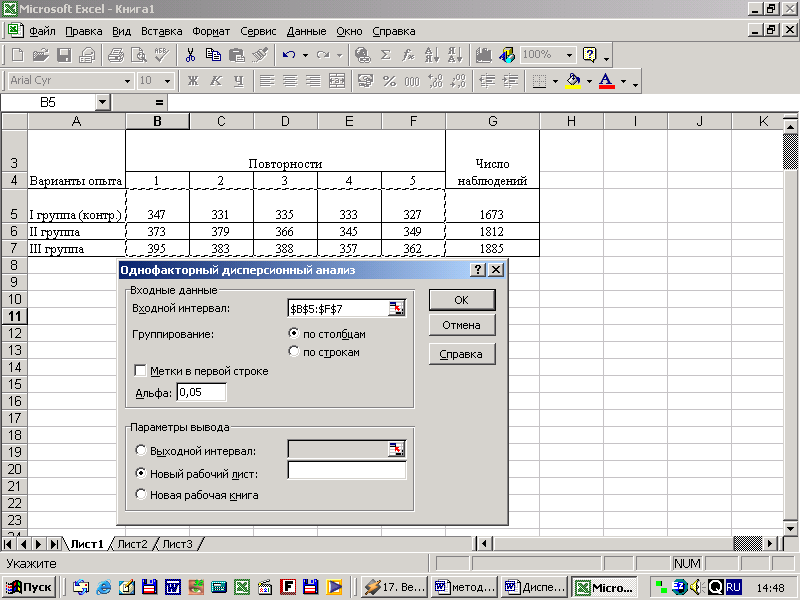
Рисунок 9 — Выбор сходного интервала для проведения анализа
Группирование
Установите переключатель в положение «по столбцам» или «по строкам» в зависимости от расположения данных во входном диапазоне.
Метки в первой строке/Метки в первом столбце
Установите переключатель в положение «Метки в первой строке», если первая строка во входном содержит названия столбцов. Установите переключатель в положение «Метки в первом столбце», если названия строк находятся в первом столбце входного диапазона. Если входной диапазон не содержит меток, то необходимые заголовки выходном диапазоне будут созданы автоматически.
Выходной диапазон
Введите ссылку на ячейку, расположенную в левом верхнем углу выходного диапазона. Размеры выходной области будут рассчитаны автоматически, и соответствующее сообщение появится на экране в том случае, если выходной диапазон занимает место существующих данных или его размеры превышают размеры листа.
Установите переключатель, чтобы открыть новый лист в книге вставить результаты анализа, начиная с ячейки . Если в этом есть необходимость, введите имя нового листа в поле, расположенном напротив соответствующего положения переключателя.
Новая книга
Установите переключатель, чтобы открыть новую книгу и вставить результаты анализа в ячейку на первом листе в этой книге.
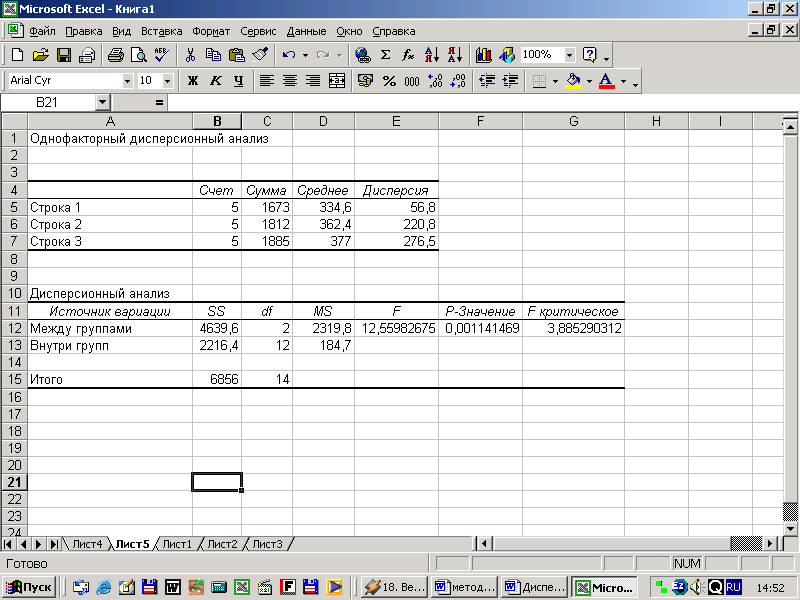
Рисунок 10 — Результаты однофакторного дисперсионного анализа.
В результате обработки данных получили следующее:
Таблица 1. Значения в СТРОКЕ 1 означают: графа «Счёт» показывает, что в первом варианте представлено пять показателя, общая сумма которых равна 1673 – графа «Сумма», 334,6- среднее значение по показателям первого варианта — графа «Среднее». В графе «Дисперсия», рассчитана частная дисперсия по генеральной совокупности первого варианта, она равна 56,8. Аналогичную информацию несут строки 2 и 3.
Таблица 2.Дисперсионный анализ представляет результаты дисперсионного анализа однофакторного комплекса, в котором первая колонка «Источник вариации» содержит наименования дисперсий. Графа «SS» — это сумма квадратов отклонений, «df» — степень свободы, графа «MS» — средний квадрат, «F» — критерий фактического F – распределения. «P- значение» — вероятность того, что дисперсия воспроизводимая уравнением равна дисперсии остатков. Определяет вероятность того, что полученная количественная определённость взаимосвязи между факторами и результатом может считаться случайной. «F- критическое»- это значение F- теоретического, которое в последствии сравнивается с F-фактическим.
Таким образом получаем:
1.Между группами (межгрупповой дисперсии): сумма квадратных отклонений – 4639,6; количество степеней свободы – 2; средний квадрат – 2319,8.
2.Внутри групп (остаточная дисперсия): сумма квадратных отклонений – 2216,4; количество степеней свободы – 12; средний квадрат – 184,7.
3.Общая дисперсия: сумма квадратных отклонений – 6856; количество степеней свободы – 14.
4.(1-P)- доверительная вероятность, с которой уравнению следует верить или доверительная вероятность. Для данного расчёта она равна (0,00114146866890166).
5.Теоретическое значение F при вероятности суждения 95% исходя из 2-х степеней свободы для межгрупповой дисперсии (числитель) и 12 степеней для остаточной дисперсии (знаменатель), равна 3,88. В свою очередь F-фактическое по данным расчёта – 12,55. При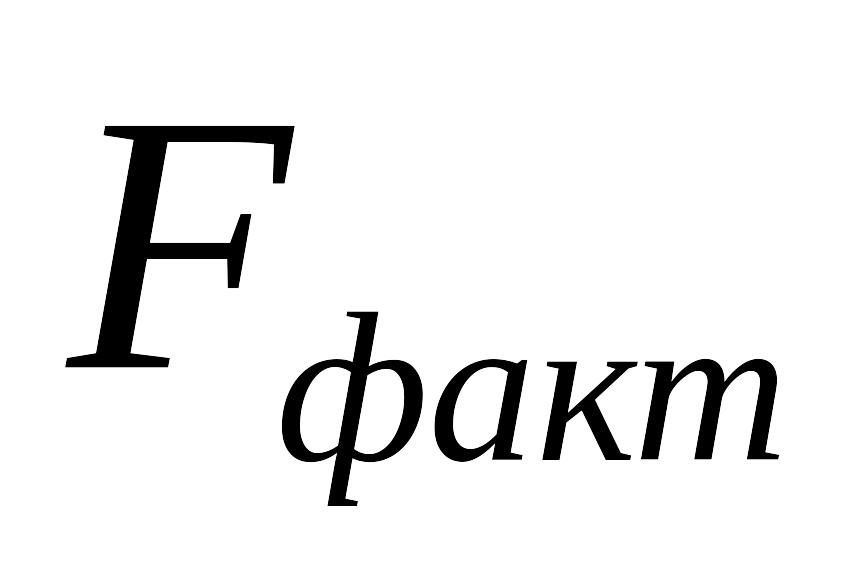 
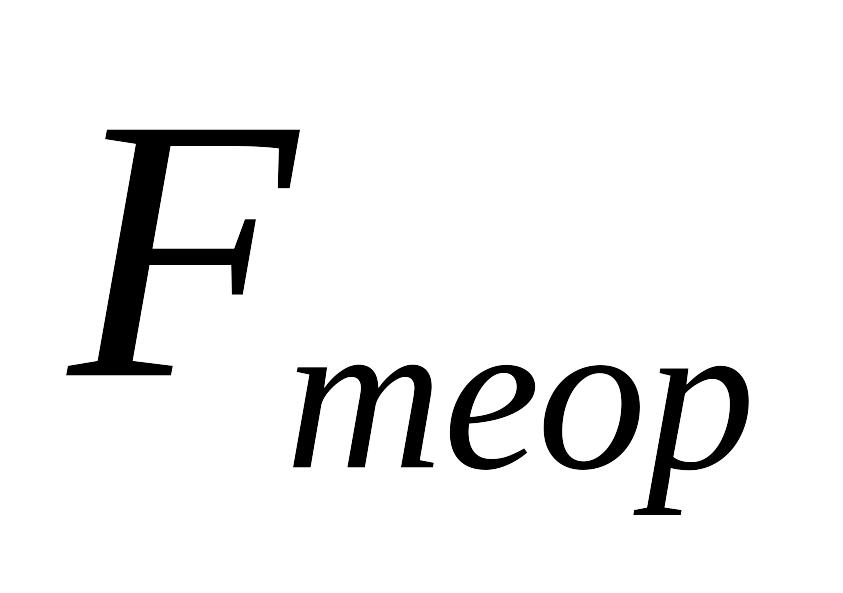в опыте есть существенные различия по вариантам на 5%-ом уровне значимости. Следовательно необходимо рассчитывать ошибку опыта, ошибку разности средних, HCP (наименьшую существенную разность) для 5%-го уровня значимости в абсолютных и относительных показателях.
Источник: studfile.net
Расчет дисперсии в Microsoft Excel
Среди множества показателей, которые применяются в статистике, нужно выделить расчет дисперсии. Следует отметить, что выполнение вручную данного вычисления – довольно утомительное занятие. К счастью, в приложении Excel имеются функции, позволяющие автоматизировать процедуру расчета. Выясним алгоритм работы с этими инструментами.
Вычисление дисперсии
Дисперсия – это показатель вариации, который представляет собой средний квадрат отклонений от математического ожидания. Таким образом, он выражает разброс чисел относительно среднего значения. Вычисление дисперсии может проводиться как по генеральной совокупности, так и по выборочной.
Способ 1: расчет по генеральной совокупности
Для расчета данного показателя в Excel по генеральной совокупности применяется функция ДИСП.Г. Синтаксис этого выражения имеет следующий вид:
Всего может быть применено от 1 до 255 аргументов. В качестве аргументов могут выступать, как числовые значения, так и ссылки на ячейки, в которых они содержатся.
Посмотрим, как вычислить это значение для диапазона с числовыми данными.
- Производим выделение ячейки на листе, в которую будут выводиться итоги вычисления дисперсии. Щелкаем по кнопке «Вставить функцию», размещенную слева от строки формул.
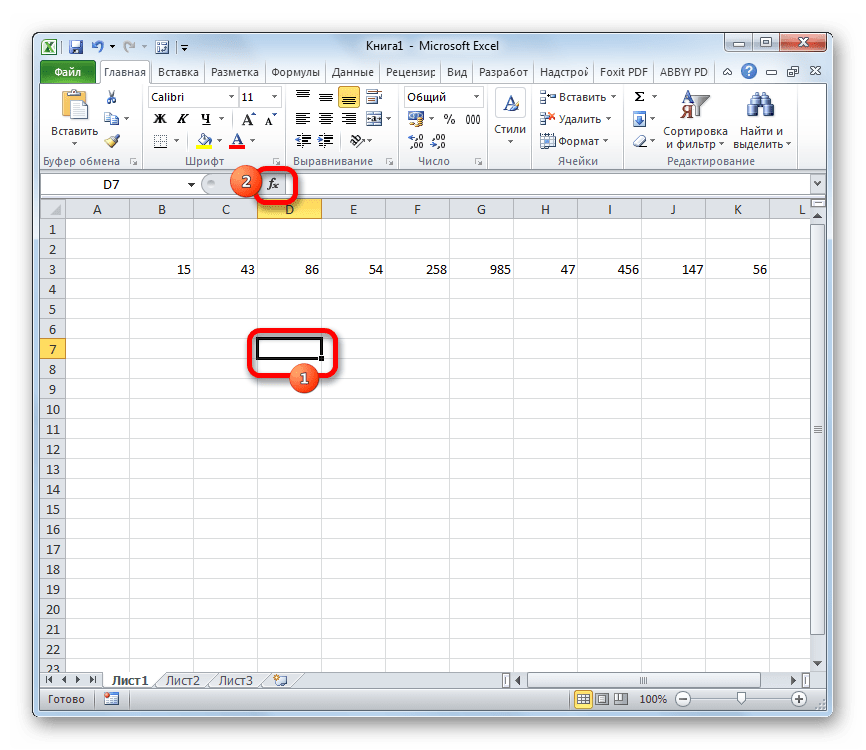
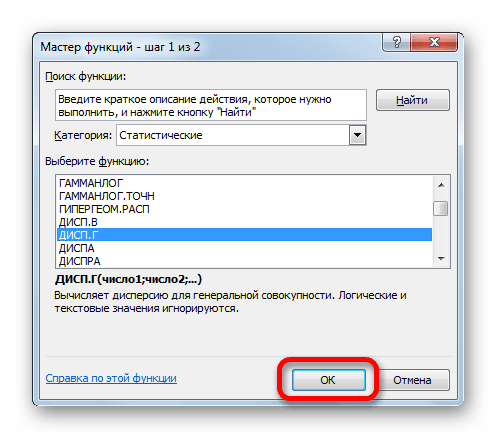
- Запускается Мастер функций. В категории «Статистические» или «Полный алфавитный перечень» выполняем поиск аргумента с наименованием «ДИСП.Г». После того, как нашли, выделяем его и щелкаем по кнопке «OK».
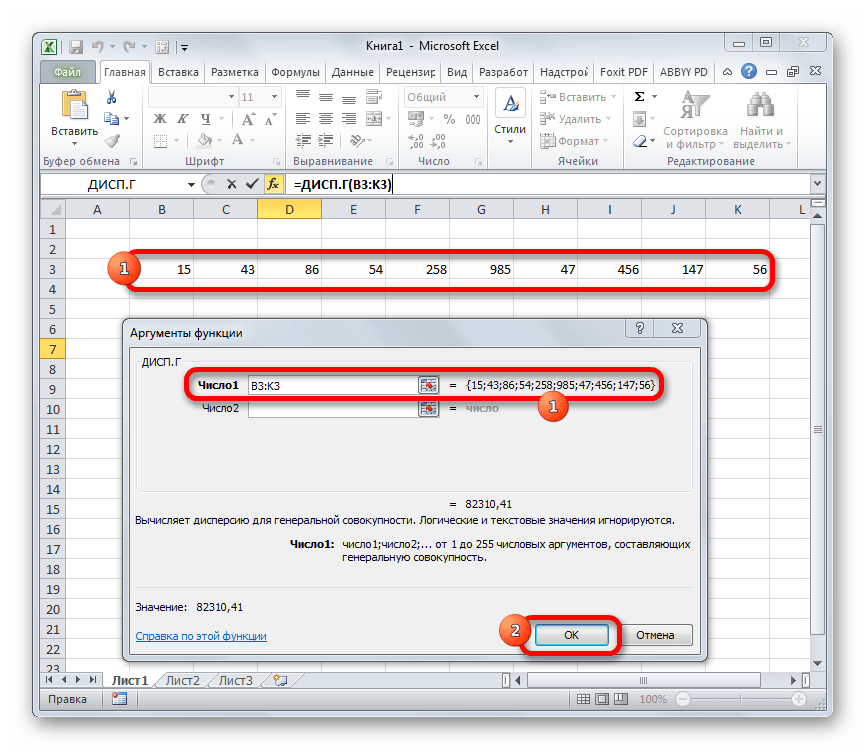
- Выполняется запуск окна аргументов функции ДИСП.Г. Устанавливаем курсор в поле «Число1». Выделяем на листе диапазон ячеек, в котором содержится числовой ряд. Если таких диапазонов несколько, то можно также использовать для занесения их координат в окно аргументов поля «Число2», «Число3» и т.д. После того, как все данные внесены, жмем на кнопку «OK».
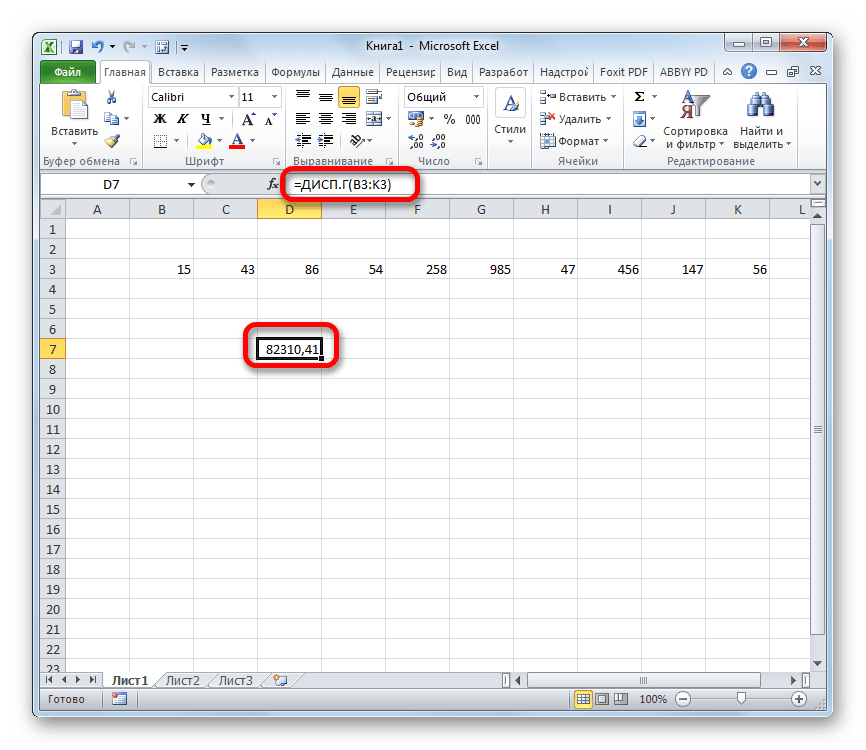
- Как видим, после этих действий производится расчет. Итог вычисления величины дисперсии по генеральной совокупности выводится в предварительно указанную ячейку. Это именно та ячейка, в которой непосредственно находится формула ДИСП.Г.
Способ 2: расчет по выборке
В отличие от вычисления значения по генеральной совокупности, в расчете по выборке в знаменателе указывается не общее количество чисел, а на одно меньше. Это делается в целях коррекции погрешности. Эксель учитывает данный нюанс в специальной функции, которая предназначена для данного вида вычисления – ДИСП.В. Её синтаксис представлен следующей формулой:
Количество аргументов, как и в предыдущей функции, тоже может колебаться от 1 до 255.
- Выделяем ячейку и таким же способом, как и в предыдущий раз, запускаем Мастер функций.
- В категории «Полный алфавитный перечень» или «Статистические» ищем наименование «ДИСП.В». После того, как формула найдена, выделяем её и делаем клик по кнопке «OK».
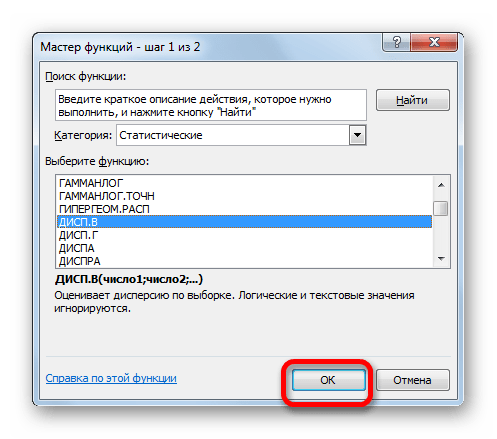
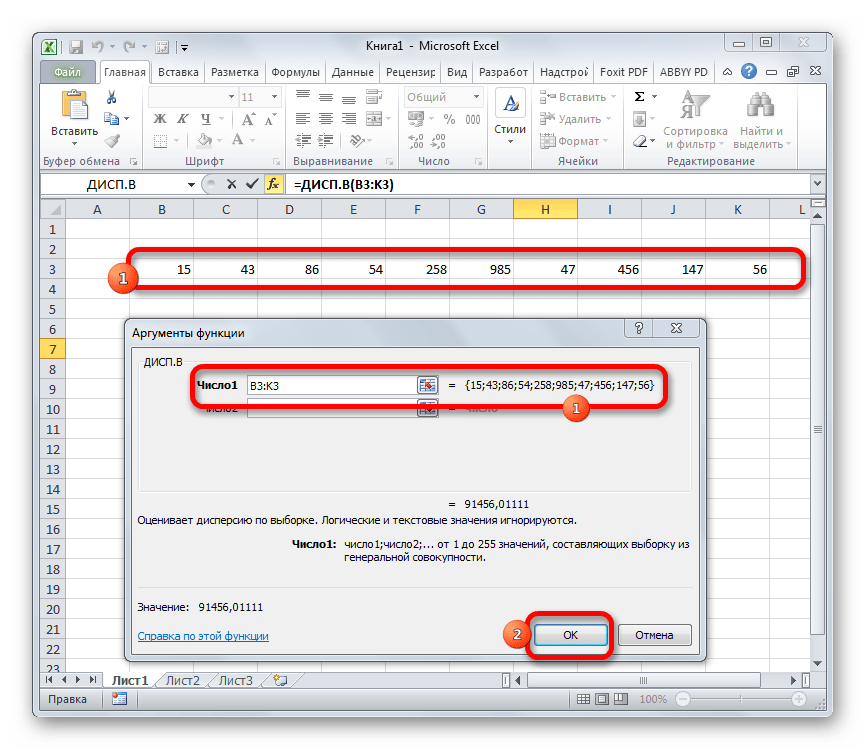
- Производится запуск окна аргументов функции. Далее поступаем полностью аналогичным образом, как и при использовании предыдущего оператора: устанавливаем курсор в поле аргумента «Число1» и выделяем область, содержащую числовой ряд, на листе. Затем щелкаем по кнопке «OK».
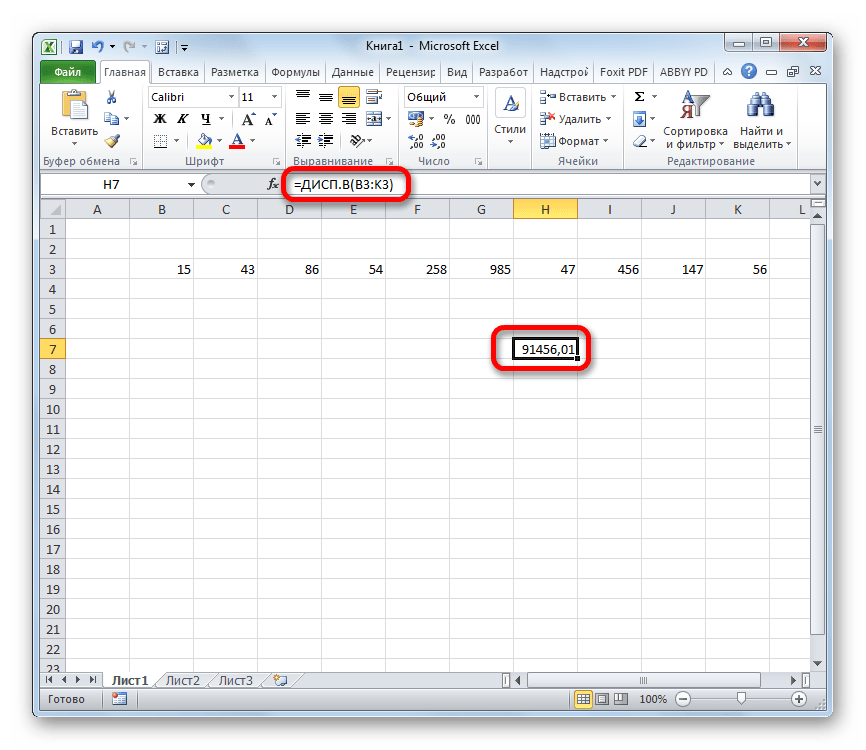
- Результат вычисления будет выведен в отдельную ячейку.
Как видим, программа Эксель способна в значительной мере облегчить расчет дисперсии. Эта статистическая величина может быть рассчитана приложением, как по генеральной совокупности, так и по выборке. При этом все действия пользователя фактически сводятся только к указанию диапазона обрабатываемых чисел, а основную работу Excel делает сам. Безусловно, это сэкономит значительное количество времени пользователей.
Источник: lumpics.ru