Как пользоваться программой алгоритм

Графическая среда разработки программного обеспечения для микроконтроллеров AVR

• Поддерживаемые операционные системы: Windows 95/98/2000/NT/ME/XP
• Лицензия: Freeware
• Язык интерфейса: английский, русский
• Языки программирования: графический ассемблер
• Основные функции:

• графический редактор код программы
• компилятор
• симулятор для отладки введенного алгоритма
• программирование через COM-порт с использованием простейшего адаптера (7 резисторов, 3 диода; схема приведена в документации)
• отладка алгоритма на кристалле с использованием еще более простого адаптера (1 или 2 диода, 2 или 4 резистора; схема приведена в документации)

Algorithm Builder — бесплатная среда (условия распространения Freeware) для МК AVR, которая обеспечивает полный цикл разработки микропрограммного обеспечения, в т.ч. такие этапы как ввод алгоритма, отладка и внутрисхемное программирование. Разработку программы можно вести как на уровне ассемблера, так и на макро-уровне, при котором возможна работа со знакопеременными величинами произвольной длины. Это приближает возможности программирования к языку высокого уровня.

Создание циклических алгоритмов для исполнителя Кенгуру

Отличительной чертой Algorithm Builder является возможность ввода программы графическим способом, в виде алгоритм с древовидной структурой. В результате вся логическая структура программы становится полностью наглядной. Такой способ программирования максимально близок к природе человеческого восприятия и, поэтому, он намного проще в освоении, если сравнивать с классическим ассемблером. Ожидаемое время сокращения времени создания микропрограммного обеспечения по сравнению с классическим ассемблером составляет 3-5 раз.

Среда предназначена для работы под ОС Windows 95/98/2000/NT/ME/XP. Для нормальной работы редактора требуется наличие шрифта «Courier».

Снимок экрана IDE AlgorithmBuilder:

Файлы для скачивания:

Ссылка	Операционная система	Поддерживаемые МК
Версия 5.43, 2 января 2010 г., 3 Мбайт	Windows 95/98/2000/NT/ME/XP	см. прим.
Бета версия 5.44, 14 марта 2010 г., 3.1 Мбайт	Windows 95/98/2000/NT/ME/XP	добавлена поддержка ATmega48P, ATmega88P, ATmega168P и ATmega328P
Документация на русском языке, 0.2 Мбайт
Статья в журнале Atmel Application Journal на английском языке, 1.5Мбайт

• Серия AT90

• AT90CAN128, AT90PWM3, AT90S1200, AT90S2313, AT90S2323, AT90S2333, AT90S2343, AT90S4414, AT90S4433, AT90S4434, AT90S8515, AT90S8535, AT90USB64, AT90USB82, AT90USB128, AT90USB162

• ATmega8, ATmega16, ATmega32, ATmega48, ATmega64, ATmega88, ATmega103, ATmega128, ATmega161, ATmega162, ATmega163, ATmega164P, ATmega165, ATmega168, ATmega323, ATmega324P, ATmega325, ATmega328P, ATmega603, ATmega640, ATmega644, ATmega644P, ATmega645, ATmega1280, ATmega1281, ATmega1284P, ATmega2560, ATmega2561, ATmega3250, ATmega6450, ATmega8515, ATmega8535

• ATtiny10, ATtiny11, ATtiny12, ATtiny13, ATtiny15, ATtiny22, ATtiny24, ATtiny25, ATtiny26, ATtiny28, ATtiny44, ATtiny45, ATtiny84, ATtiny85, ATtiny261, ATtiny461, ATtiny861, ATtiny2313

Источник: www.gaw.ru

Работа с программой «Алгоритм 2» (Урок № 1 вступление)

Algorithm Builder. Урок 1 — Введение

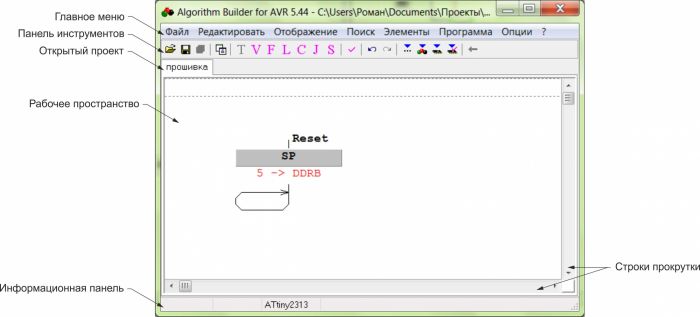
Думаю, в наше время нет радиолюбителя, который никогда не сталкивался с микроконтроллерами. Рано или поздно, но это происходит. Когда я в первый раз увидел схему с микроконтроллером, тут же закрыл страницу браузера, с мыслью: «А, все равно не соберу». Но время шло, схем с применением микроконтроллеров становилось все больше, и я все-таки решил начать. На деле все оказалось совсем не таким сложным, как я думал. Для начала давайте разберемся: что вообще такое микроконтроллер (МК)? По сути, это миниатюрный компьютер, предназначенный для выполнения простейших задач. Все необходимое для работы микроконтроллера заключено в одном корпусе. В микроконтроллере имеется различная периферия — порты вводавывода, таймеры, интерфейсы связи и т.д. Микроконтроллер имеет три вида памяти, это RAM (оперативная память), FlashROM (Память программы), EEPROM (энергонезависимая память). Главное отличие микроконтроллера от обычной микросхемы — это то, что микроконтроллер работает не по жесткой логике, установленной на заводе, а программируется. Программа, классически пишется в специальной среде на компьютере на одном из языков программирования, после чего переводится на машинный язык(компилируется) и записывается в память контроллера. В этом курсе все будет немного по-другому — программа будет не писаться, а буквально рисоваться в виде блок-схемы. Благодаря такому подходу программа выглядит более наглядно, а время на разработку программы сокращается в 3-5 раз, по сравнению с классическими приемами программирования. Algorithm Builder — среда программирования Algorithm Builder производит полный цикл разработки, начиная от ввода алгоритма, включая процесс отладки и заканчивая записью программы в память. Начнем с краткого обзора интерфейса программы Главное меню

• Файл. Служит для открытия, сохранения, закрытия проектов и отдельных алгоритмов, а так же выхода из программы.
• Редактировать. Действия, связанные с редактированием алгоритма: вырезать, копировать, выделить и т.д
• Отображение. Переключение алгоритм/таблица с переменными(о ней ниже) + шаблоны операций и условий.
• Поиск. Тут пояснять не нужно.
• Элементы. Алгоритм рисуется из специальных элементов: Текст, Вершина, Поле, Метка, Условие, Вектор б/у (безусловного) перехода, Настройщик. Со всеми ними мы познакомимся в процессе обучения. В меню находится еще несколько важных пунктов: Деактивировать, Макро, Прерывания.Деактивировать — данный компонент не будет компилироваться. Макро — для создания макросов. Прерывания — содержит список названии всех прерываний микроконтроллера. Об этой функции вы узнаете в следующих уроках, сейчас лишь скажу, что это чрезвычайно важная и необходимая для работы вещь.
• Программа. Действия, связанные с программой — компиляция (перевод на машинный язык), симуляция работы программы, чтение памяти контроллера (Flash и EEPROM) и т.д.
• Опции. Настройки проекта и среды.
• ?. Информация о Algoritm Builder и справка.

Панель инструментов

В пояснениях не нуждается. При наведении курсора на элементы панели всплывают подсказки.

Открытый проект

Тут есть особенность. Нельзя открыть два проекта одновременно.Чтобы открыть/создать новый проект нужно закрыть старый. После открытия проекта вы можете открыть/создать лишь отдельный файл-алгоритм. Файл проекта имеет расширение .alp, а отдельный файл-алгоритм имеет расширение .alg

Работа с переменными и константами

Организуется в виде специальной таблицы (переключить можно клавишей F12, либо через меню, либо клавишей на панели инструментов). Таким образом, сам алгоритм освобождается от лишних записей.

Огромное число меток, благодаря которым возможны переходы от одной части программы к другой, сильно загромождают код, и наглядность программы теряется. В Algorithm Builder переходы осуществляются намного проще — стрелкой (вектором). Но переходы по именованным меткам так же возможны.

Симуляция работы программы

Симулятор показывает все изменения, происходящие внутри виртуального микроконтроллера. Что бы проверить работу программы не обязательно даже покупать микроконтроллер! Симуляция может выполняться пошагово (с заходом в функции или нет), до установленной точки останова или до выделенного участка.

Отладка

Algorithm Builder обладает системой мониторной отладки на кристалле (On Chip debug) которая позволяет наблюдать содержимое памяти реального микроконтроллера в заданных точках. При этом для связи микроконтроллера с компьютером используется всего одна ножка микроконтроллера, причем по выбору пользователя. Мониторная отладка может быть применена практически к любому микроконтроллеру. Это программный вариант протокола debugWIRE.

Так почему же Algorithm Builder малоизвестен среди радиолюбителей? Во-первых, до 2010 программа была платной. Сегодня ПО распространяется абсолютно свободно. Во-вторых, отсутствие официальной поддержки программы. Вы не найдете ни одного апнота производителя в котором бы использовался Билдер.

Интернет ресурсы, посвященные данной программе, можно пересчитать по пальцам.

Стоит немного рассказать о необходимых материалах и инструментах

Первое что понадобится — это паяльник. Основной инструмент радиолюбителя. Мощность паяльника должна быть в приделах 30-60 Вт. Почему нельзя больше? Мощный паяльник нагревается сильней, и повреждает дорожки платы и применяемые детали.

Да и паять им не так удобно — такой паяльник намного больше и тяжелее. Подробнее о паяльниках и пайке

Для того, чтобы загрузить программу в микроконтроллер нужен программатор — в простейшем варианте состоит всего из нескольких резисторов и диодов (на порт LPT и COM). Если у Вас на компьютере нет порта COM либо LPT, USB программатор можно заказать на eBay, DealExtreame или Aliexpress (Поисковой запрос»avr programmer»; стоит примерно 4-6$). О выборе и сборке программатора я напишу в следующем уроке.

Для связи микроконтроллера с компьютером (например, чтобы передать от микроконтроллера к компьютеру данные с датчика температуры) необходим специальный переходник. Он не имеет прямого отношения к этому курсу, однако для некоторых устройств он может быть полезен. Называется он USB-UART (для USB) или COM-UART (для COM порта). Подробней я расскажу об этом в следующих уроках.

Ну и самое главное — микроконтроллер. В этом учебном курсе мы будем использовать микроконтроллер ATmega 88. Почему именно он? Это один микроконтроллер из серии ATmega 48, ATmega 88, ATmega 168, ATmega 328. Это значит, что если вы знаете один микроконтроллер из серии — вы знаете и всю серию! Отличаются они лишь объемом памяти.

Если вы разрабатываете программу и понимаете, что программа не влезает в память — вы всегда сможете перейти на более «взрослый» микроконтроллер из серии, не меняя при этом самой программы.

Теги:

dossalab Опубликована: 21.07.2014 0

Вознаградить Я собрал 0 0

Оценить статью

• Техническая грамотность

Источник: cxem.net

Алгоритмы для веб-разработчиков простыми словами

Здравствуйте, друзья! Данным постом мы открываем цикл статей об алгоритмах и структурах данных.

В этой статье мы поговорим о том, зачем вообще их нужно знать веб-разработчикам, и затронем тему оценки сложности алгоритмов и Big O нотации.

Зачем мне алгоритмы? Я фронтендер!

Вы наверняка задумались: «А зачем мне нужно тратить своё время на изучение этих сложных алгоритмов, если я работаю с фронтендом? Как знание графов и бинарных деревьев поможет мне лучше отцентровать одну div-ку внутри другой div-ки?»

С одной стороны, знание алгоритмов и структур данных действительно напрямую не пригодится вам в практической работе. Но с другой стороны, существует одна весомая причина инвестировать немного своего времени в их изучение: знание алгоритмов и структур данных сделает вас лучше как разработчика.

Многие веб-разработчики на таких форумах, как Reddit и Stack Overflow, отмечали, что, освоив даже на базовом уровне эти фундаментальные основы программирования, чувствовали себя увереннее, профессиональнее и писали более чистый и структурированный код.

Также это помогло им прокачать главный скилл разработчика – умение логически думать и решать сложные технические задачи.

Кстати, именно по этой причине многие крупные IT-компании требуют от своих потенциальных сотрудников знания фундаментальных основ computer science, к которым как раз относятся алгоримты и структуры данных, и с пристрастием спрашивают их на собеседованиях (даже на позицию фронтенд-разработчика!).

Ведь они ищут лучших из лучших, и знание алгоритмов как раз делает вас лучше как разработчика. Тем более, лучше инвестировать свое свободное время в новые знания и навыки, чем в сериалы на Netflix.

И на этой прекрасной ноте давайте перейдем к основной теме статьи.

Что такое алгоритмы и структуры данных

Алгоритм — это совокупность последовательных операций, направленных на решение определенной задачи.

Структуры данных — это особый способ организации и хранения данных в компьютере, который обеспечивает эффективный доступ к этим данным и их изменение. Для оценки сложности и скорости работы алгоритма используют так называемую «О-нотацию» или «О-большое».

Эта запись имеет вид O(n) , где n – это количество операций, которое предстоит выполнить алгоритму. Важное замечание: O(n) всегда описывает худший возможный случай выполнения алгоритма. Это дает нам гарантию, что наш алгоритм никогда не будет работать медленнее O(n) .

Скорость работы алгоритмов измеряется не в секундах, а в темпе роста количества операций. Т.е. нас интересует, насколько быстро возрастает время выполнения алгоритма с увеличением размера входных данных.

Вот так выглядит время работы некоторых алгоритмов:

O(1) – константное время. Например, чтение данных из ячейки в массиве.

O(log n) – логарифмическое время. Например, бинарный поиск.

O(n) – линейное время. Например, поиск наименьшего или наибольшего элемента в неотсортированном массиве.

O(n * log n) – линейно-логарифмическое время. Например, быстрая сортировка.

O(n2) – квадратичное время. Например, сортировка пузырьком.

O(n!) – факториальное время. Например, решение задачи коммивояжера полным перебором.

Алгоритм линейного поиска

Давайте для начала рассмотрим такой простейший алгоритм, как линейный поиск элемента в массиве, и реализуем его на JavaScript.

Итак, есть массив чисел, и нам нужно найти в нем конкретное число.

Создадим функцию линейного поиска и назовем ее linearSearch . Эта функция будет принимать в себя два параметра: array (т.е. сам массив элементов, в котором ведется поиск) и item (элемент, который мы ищем в этом массиве).

Линейный поиск происходит достаточно предсказуемо: мы используем цикл for, в котором пробегаемся по элементам массива и сравниваем каждый элемент с искомым.

Далее инициализируем счётчик и установим его исходное значение, которое будет равно нулю, так как мы собираемся проверять массив с самого первого элемента.

Наш цикл будет выполняться до тех пор, пока не пройдет по всем элементам массива. В качестве конечной точки мы используем значение array.length , которое возвращает количество элементов в массиве. Так как массив array начинается с нулевого индекса, то мы используем при сравнении знак «

После каждой итерации цикла увеличиваем значение переменной i на единицу.

Далее с помощью условной конструкции if будем проверять на истинность одно условие. Данная проверка будет выполняться при каждой итерации цикла, но код внутри нее сработает только один раз, после чего функция завершится.

Здесь мы сравниваем каждый элемент массива ( array[i] ) c искомым элементом ( item ) и, если эти элементы совпадают, то возвращаем i (индекс массива, по которому находится этот искомый элемент item ).

Если же искомый элемент не был найден, то по завершении работы цикла мы возвращаем -1.

Дальше нам остается только вызвать функцию linearSearch , первым параметром передать в нее массив элементов, а вторым параметром — искомое число.

Затем, с помощью функции console.log , выводим результат в консоль.

Продублируем код для копирования:

const array = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]; function linearSearch(array, item) < for (let i = 0; i < array.length; i++) < if (array[i] === item) < return i; >> return -1; > console.log(linearSearch(array, 5)); // Вызываем функцию и получаем 5.

Как видите, алгоритм линейного поиска довольно прост в реализации. Сложность данного алгоритма: линейное время или O(n) .

Давайте теперь рассмотрим более сложный и интересный алгоритм, который еще называют алгоритмом бинарного поиска.

Алгоритм бинарного поиска

Бинарный (или двоичный) поиск — это алгоритм, при котором массив данных будет последовательно делиться пополам до тех пор, пока не будет обнаружен искомый элемент.

Важное замечание: данный алгоритм будет работать только для отсортированного массива.

Бинарный поиск может быть реализован следующим образом:

0. Берём исходный массив отсортированных данных (например, по возрастанию).

1. Делим его на две части и находим середину.

2. Сравниваем элемент в середине с искомым элементом.

3. Если искомое число меньше этого центрального элемента — продолжаем искать элемент в левой части массива. Для этого мы делим левую часть массива на 2 части. Если искомый элемент больше центрального элемента, то мы отбрасываем левую часть массива и продолжаем поиск в правой.

И повторяем данную процедуру до тех пор, пока не найдем искомый элемент. Как только мы его нашли, то возвращаем индекс в массиве, по которому он находится. Если же данный элемент не будет найден, то возвращаем -1.

Давайте сначала взглянем на реализацию данного алгоритма, а потом разберем ее детально.

const arr = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]; const binarySearch = (arr, value) => < let start = 0; let end = arr.length — 1; while (start else < start = middle + 1; >> return -1; >; console.log(binarySearch(arr, 5)); // 5

Итак, у нас есть массив чисел arr, отсортированный по возрастанию. Как вы помните, если заранее не отсортировать массив, то бинарный поиск не будет работать.

Создаем функцию binarySearch и передаем в нее два параметра: отсортированный массив arr и искомый элемент value.

Затем определяем следующие переменные:

Так как мы должны найти центральный элемент, то сначала необходимо определить начальный и конечный элементы.

Задаем таким образом начальный элемент и устанавливаем его значение равным нулю, так как наш массив начинается с нулевого индекса.

let end = arr.length — 1;

Затем определяем конечный элемент. Его позиция будет вычисляться по длине массива arr.length — 1 .

Далее мы создадим цикл while, который будет работать до тех пор, пока начальная и конечная позиция массива не сравняются ( start

Внутри цикла мы будем высчитывать позицию центрального элемента в массиве и сохранять ее в переменную middle. Для этого мы складываем начальную позицию с конечной и делим результат на две части.

Результат обернем в функцию Math.floor() , так как в результате деления у нас может получиться дробное число. С помощью данной функции мы округляем полученное число до нижней границы.

Далее с помощью условной конструкции if создаем проверку: если центральный элемент в массиве по индексу middle равен искомому элементу, то мы возвращаем индекс найденного элемента, сохраненный в переменной middle. И на этом наша функция завершает свою работу.

Если на данной итерации цикла мы не нашли искомый элемент, то необходимо выполнить еще одну проверку с помощью условной конструкции if . Если искомый элемент меньше, чем элемент, находящийся в середине, то это значит, что нам нужно продолжить поиск в левой части массива, а правую можно отбросить.

Для этого нам нужно изменить значение переменной end . В итоге мы получим end = middle + 1 . А в блоке else мы прописываем такое же условие, только для случая, если искомый элемент будет больше, чем элемент, находящийся в середине. Тогда мы отбрасываем левую часть массива и продолжаем поиск в правой.

После завершения цикла while возвращаем -1 на случай, если искомое число не будет найдено в массиве. Далее вызываем функцию binarySearch и передаем в нее два параметра: массив элементов и искомое число.

И выводим результат в консоль.

Что касается оценки сложности приведенных алгоритмов: бинарный поиск эффективнее линейного, поскольку массив данных на каждом шаге разделяется надвое и одна половина сразу отбрасывается.

Последовательная сложность бинарного поиска в худшем и среднем случаях равна O(log n) , в лучшем — O(1) (если обнаруживаем искомый элемент на первой итерации). Для сравнения: вычислительная сложность линейного поиска, как вы помните, равна O(n) .

На этом мы закончили первую статью из нашего цикла статей по алгоритмам. Спасибо за внимание.

Источник: habr.com