Подпись у каждого человека также уникальна, как и его биохарактеристики. Она является традиционным способом подтверждения документов и некоторых операций и своеобразным способом идентификации личности. Копирование подписи – это ее фактическое подделывание. Подделка и использование заведомо подложных документов преследуется по закону, в том числе предусматривается уголовная ответственность.

Статьи по теме:
- Как скопировать подпись
- Как делать и вставлять подпись на компьютере
- Как придумать свою роспись
Инструкция
Для копирования подписи понадобятся: лист бумаги, куда необходимо поместить копию подписи, и авторучка – для простого способа копирования; компьютер, сканер, принтер, бумага и ручка – для более сложного способа.Сканируйте образец подписи, поместите образец в компьютер и распечатайте лист с подписью на чистом листе или бланке. При распечатывании на принтере используйте цвет самой малой насыщенности, предпочтительно синий или фиолетовый, так, чтобы подпись была еле различима на фоне бумаги. Распечатав бланк с подписью, аккуратно обведите ее авторучкой.
БУХГАЛТЕР. Как правильно подделать подпись?
Если используете более простой способ, то положите оригинал с подписью на чистый лист и, используя авторучку со стержнем без чернил, обведите оригинал подписи, слегка продавливая написание, затем оттиск подписи обведите авторучкой.
Аналогичный по сложности способ: при дневном свете закрепить документ с оригиналом подписи на стекле окна, наложить сверху чистый лист и воспроизвести авторучкой просвечивающуюся подпись. Для удобства и аккуратности подписи можно на стекле воспроизвести ее авторучкой со стержнем без чернил, а потом на более удобной поверхности обвести оттиск авторучкой с пастой. Если есть стеклянный стол, под ним располагаем источник света, кладем на стол документ с оригиналом подписи и проводим те же самые операции, что и на стекле окна.
Самый простой по механизму и самый сложный по качеству копирования способ (для натур с высоким художественным потенциалом) – поставить подпись по образцу.
Полезный совет
Любое копирование подписи можно распознать. Для этого проводятся почерковедческие и технико-почерковедческие экспертизы, так что избежать риска обнаружения подмены не удастся. Особые виртуозы в области получения чужих подписей просто незаметно подкладывают на подпись необходимому лицу чистый лист бумаги или бланк документа.
Совет полезен?
Статьи по теме:
- Как перенести печать
- Как доказать подделку своей подписи
- Как вставить подпись в электронный документ
Добавить комментарий к статье
Похожие советы
- Что грозит за подделку подписи
- Как создать графическую электронную подпись
- Имеет ли факсимиле юридическую силу
- Как сделать подпись
- Как придумать свою подпись
- Как скопировать печать
- Как создать электронную подпись
- Как изменить подпись в The Bat
- Как изменить текст после сканирования
- Что такое факсимильная подпись
- Как выглядит электронная цифровая подпись
- Как сделать электронную копию документа
Источник: www.kakprosto.ru
как подделать подпись из стирачки
Подделываем вашу подпись при помощи шарнирного механизма. Теорема Кемпе
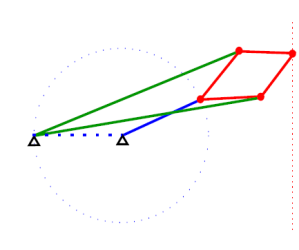
В этом посте я расскажу про программу, которая подделывает любую подпись при помощи шарнирного механизма. Программа основана на теореме Кемпе, доказанной в середине 19-го века.
Теорема Кемпе
С развитием техники и появлением поездов у пытливых умов встала очень интересная проблема, а можно ли создать шарнирный механизм, который переводит круговое движение, в движение по прямой, выражаясь по-другому, рисует прямую. Шарнирный механизм — это много скрепленных между собой палочек, которые могут свободно вращаться в точках креплений. Многие ученые бились над этой проблемой, придумывая хитроумные механизмы, но все они рисовали неточные прямые. Вот, например, механизмы Ватта, Чебышева и Хойкена:
Многие математики считали, что проблема создания шарнирного механизма, рисующего идеальную прямую линию, является в принципе неразрешимой, пока в середине 19-го века не был открыт гениальный механизм Липкина-Посселье, который рисует точную прямую:
В этом механизме все палочки одинакового цвета имеют одинаковую длину. Доказать, что механизм действительно рисует прямую можно прямыми выкладками, как говорится, в лоб. Но люди, знакомые с преобразованием инверсии, могут увидеть довольно четкую логику в доказательстве.
К моменту изобретения механизма Липкина-Посселье уже смазочные материалы были настолько хороши, что в технике могли обходиться без этого идеального преобразователя в прямолинейное движение. Ведь можно через еще одну палочку передавать почти прямолинейное движение на поршень. Эта палочка не будет всегда идеально параллельной направляющей поршня, но в этом ничего страшного нет. В итоге механизм Липкина-Посселье так и не нашел широкого применения в технике, но зато оказал огромное влияние на математику.
Через несколько лет математик-адвокат Кемпе приводит алгоритм, как абсолютно для любой алгебраической кривой на плоскости построить шарнирный механизм, который умеет рисовать только эту кривую и больше ничего не умеет. Иными словами, существует механизм, ограниченный в движении одной степенью свободы.
Двигаясь вдоль этой степени свободы механизм рисует нашу алгебраическую кривую. Прекрасное изложение доказательства Кемпе я нашел в этой статье. Напомним читателю, что алгебраические кривые, о которых идет речь в теореме Кемпе — это кривые, заданные уравнением , где — любой многочлен. Например, — это окружность радиуса , — наклоненная прямая, — парабола. В своем доказательстве Кемпе использует много интересных идей, но ключевым инструментом построения является уже известный нам механизм Липкина-Посселье.
Процесс

Как только я узнал о теореме Кемпе, я сразу же захотел написать программу, в которой пользователь может нарисовать любую кривую, скажем свою подпись, а программа аппроксимирует подпись алгебраической кривой, а потом по алгоритму Кемпе построит шарнирный механизм, подделывающий ее. Мне очень хотелось сделать веб-приложение, чтобы пользователю не нужно было ничего устанавливать на компьютер, чтобы можно было зайти на сайт и запустить все «в один клик». Так как я не программист, то это еще было для меня прекрасной возможностью познакомиться с JavaScript и HTML5.
После того, как я выучил доказательство Кемпе, передо мной встала очень серьезная проблема:
как аппроксимировать подпись алгебраической кривой с хорошей точностью, быстро, да еще и на медленном JavaScript? Существует очень простой, но неподходящий нам способ аппроксимации кривой объединением маленьких окружностей, разбросанных вдоль кривой, как показано на картинке:
Каждая маленькая -ая окружность является, очевидно, алгебраической кривой, так как задается полиномиальным уравнением , где — центр окружности, а — ее радиус. Алгебраической кривой, очевидно, будет и объединение всех маленьких окружностей, так как это объединение будет задаваться полиномиальным уравнением . Но как вы видите, такой вид аппроксимации нам совершенно не подходит, потому что возникает очень много точек самопересечений. Хотелось бы иметь более «красивую» аппроксимацию. Оказывается, проблема «красивой» аппроксимации сложная как с математической точки зрения, так и с вычислительной. Чтобы как-то прочувствовать это, полезно представить алгебраическую кривую как пересечение поверхности и плоскости . Линия пересечения очень чувствительна к коэффициентам многочлена , она совершенно неконтролируемо может быть несвязной, иметь точки ответвлений, что и будет портить «красоту» аппроксимации.
После недели экспериментов с различными алгоритмами, все мои попытки хоть как-то аппроксимировать кривую оказались тщетными. Все алгоритмы работали очень медленно и плохо. Я почти сдался, предварительно запостив вопрос на mathoverflow, где традиционно сидит много профессиональных математиков.
В вопросе я вскользь упомянул, что мне это нужно для того, чтобы подделывать подписи шарнирами. Каково было моё удивление, что через день-два мне ответил математик Михаил Капович. Ответил «не в бровь, а в глаз». Как оказалось, он когда-то занимался теоремой Кемпе и вместе с Джоном Миллсоном в своей статье доказал, что можно построить шарнирные механизмы не только для алгебраических кривых, но и для кривых, которые более естественно подходят для задач аппроксимаций, а именно, для кривых, заданных параметрически полиномиальными выражениями:
Такими кривыми проще простого аппроксимировать любые непрерывные кривые, в том числе и нашу подпись. Можно аппроксимировать так называемыми полиномами Чебышева, а можно сначала приблизить рядами Фурье, а потом тригонометрические функции в рядах Фурье приблизить рядами Тейлора. Получается, что вместо того, чтобы пытаться аппроксимировать кривую алгебраическими кривыми, лучше изменить само доказательство Кемпе и научиться строить шарнирные механизмы, умеющие строить более подходящие для задач аппроксимации кривые.
Вся эта история по ощущениям была похожа на находку огромного алмаза. Но, к своему стыду, я не до конца разобрался в той статье. Статья написана довольно сложно. Но сам факт того, что существует решение моей проблемы открыл мне глаза. Я сообразил, что незначительным изменением оригинального доказательства Кемпе можно строить шарниры, рисующие косинусоидальные тригонометрические кривые, то есть кривые вида
Такими кривыми даже еще легче аппроксимировать нашу подпись (теория рядов Фурье), чем кривыми со статьи Каповича-Миллсона. Действительно, из теории рядов Фурье следует, что на отрезке функции и можно разложить в ряд по косинусам. Для точности аппроксимации имеем:
Коэффициенты и легко находятся. Нужно просто умножить равенства слева и справа на и проинтегрировать от до , тогда в правой части почти все интегралы обнулятся, кроме одного при члене в первом равенстве и при члене во втором. В итоге получится:
Я очень долго думал размещать ли в этом посте алгоритм построения шарниров, которые и строят эти тригонометрические кривые. Потом я понял, что это добавит математической скучности в текст. Люди обычно не любят в текстах такого рода читать длинные доказательства. Поэтому я обойдусь просто ссылкой (upd: зеркало). Любопытные могут посмотреть.
A вот, собственно, и само приложение, которое подделывает вашу подпись: david.wf/linkage. (upd: зеркало) Прошу заметить, мышкой можно двигать конструкцию, а скроллером — приближать и удалять (upd: степень аппроксимации тоже можно менять специальным ползунком «approximation»). Приложение работает на современных браузерах, на старых я не тестировал.
Меньше всего тормозит на хроме, так как только хром намного быстрее других браузеров рисует прямые (пруфлинк). Признаться, я потратил много сил на оптимизацию, чтобы ничего не тормозило на слабых компах, но, скажу честно, особых успехов не достиг. Еще раз подчеркну, шарнир, который строит программа ничего не умеет рисовать, кроме вашей подписи. Шарнир приводится в движение крутящимся синеньким треугольником — «двигателем».
- алгоритмы
- математические этюды
Источник: habr.com
Подделка подписей: как используют компьютерные технологии

На сегодняшний день выделяют две основные технологии подделки подписей. Рукописная технология Технология, которая имеет следующие разновидности: а) произвольное рукописное исполнение подписи, никоим образом не совпадающей с оригинальной подписью (подобный вариант используется тогда, когда лицо, подделывающее подпись, ранее не видело подлинную подпись и не располагает образцом подлинной подписи); б) исполнение подписи по памяти (подделывающий подпись ранее видел подлинную подпись, но не располагает ее образцом); в) исполнение подписи путем подражания подлинной подписи (подделывающий располагает образцом подлинной подписи) либо сразу на подделываемом документе, либо после предварительной тренировки. Техническая подделка подписи Технология, которая подразделяется на: а) рукописное копирование подлинной подписи с применением простейших технических приемов: с использованием копировальной бумаги, за счет передавливания или на просвет и т.п. б) нанесение на носителе подделываемого документа изображения подписи.
Подделка с помощью распечатки
- перья с трубчатым (фитильным) пишущим узлом (инкографы), заправляемые специальной тушью (обычно используются в так называемых самописцах);
- закрепляемые в пишущем блоке традиционные пишущие приборы с капиллярным (фломастеры или линеры) либо шариковым (шариковые и гелевые ручки, роллеры) пишущим узлом или же перьевые ручки.
С помощью плоттера можно нарисовать любую кривую.
Для того чтобы с помощью плоттера нарисовать компьютерную копию подлинной рукописной подписи, может использоваться следующая технология:
1 этап – сканируется подпись.
2 этап – на экране монитора с использованием специального программного обеспечения определяются реперные точки, направление и траектория движения пишущего блока.
Далее эта подпись в виде заданной кривой с помощью плоттера вырисовывается на поддельном документе. Подделка подписи с использованием вышеописанной технологии не требует применения дорогостоящего оборудования. Однако реализация подобной технологии на практике требует, во-первых, привлечения эксперта-почерковеда, а во-вторых, высококвалифицированного программиста.
Случай экспертного исследования документа, в котором «рукописный» текст и подпись были нарисованы с помощью плоттера, описан в отечественной специальной литературе. Фактически единственным признаком, по которому эксперты пришли к такому выводу, стало отсутствие градаций нажима при выполнении сгибательных и разгибательных движений.
Использование робототехники
Известная канадская писательница, лауреат Букеровской премии Маргарет Этвуд, пытаясь решить проблему подписания экземпляров своих книг, не выходя из дома и не выезжая в зарубежные туры, в 2004 году обратилась к одной из известных канадских фирм в области робототехники Quanser Consulting Inc.
В сентябре 2006 года состоялась презентация онлайновой дистанционной подписи экземпляров книг с использованием устройства, которое было зарегистрировано под торговой маркой LongPenTM. Причем М. Этвуд находилась в Канаде, а исполнительный пишущий механизм находился в одном из лондонских книжных магазинов.
Но не одна Quanser Consulting Inc. обратилась к теме создания роботизированной руки (robotic arm) для компьютерного копирования рукописных подписей и почерка. Американская компания Damilic Corporation разработала и реализует несколько устройств для рисовки подписей.
Robotic arm разрабатывались и выпускаются для вполне легальных целей, например, для подписания неофициальных документов, открыток, поздравлений и т.п. Но, как это неоднократно случалось со многими достижениями научно-технического прогресса, они начинают активно использоваться в противоправной деятельности. И в таких условиях практикующие юристы и эксперты, к сожалению, чаще всего оказываются в роли догоняющих, не имея возможности сработать на опережение.
Если сегодня злоумышленник воспользуется для рисовки подписи одним из вышеописанных устройств, которые имитируют, кстати сказать, и градации нажима, то автор статьи полагает, что эксперты вряд ли могут установить факт использования подобной технологии подделки, поскольку они не располагают методиками выявления следов их применения при подделке подписей и почерка.
Донна Киношита, вице-президент компании Unotchit Inc., в своем выступлении на проходившей в 2008 году в Лас-Вегасе (США) выставке Digital Signage Expo утверждала, что американские эксперты не смогли отличить подпись, исполненную с использованием LongPen, от подлинной рукописной. Возможно, это был чистой воды PR разработчиков, но о сложностях при диагностике подобной технологии компьютерной рисовки подписей сообщала в своем докладе канадский эксперт Диана Крюгер на 60-й ежегодной конференции Американской академии экспертных наук в 2008 г. (60th Annual Meeting of the American Academy of Forensic Sciences, February 18 — 23, 2008, Washington, DC).
Для того чтобы вооружить экспертов методическими рекомендациями по установлению фактов компьютерной технологии подделки рукописного почерка и подписей, необходимо проведение серьезных исследований, требующих определенных финансовых затрат, прежде всего связанных с приобретением современных robotic arm.
- подпись
- почерковедческая экспертиза
Источник: www.klerk.ru