Как писать программы для машины тьюринга

Схему примитивной рекурсии для функции q(x,y) частного от целого деления y на x выглядит следующим образом:

Функция q(x,y) примитивно рекурсивная, так как функции r(x,y), сложение, усечённая разность, sg(x) и отрицание являются примитивно рекурсивными.

Проверим данную схему рекурсии, будим вычислять значения q(x,y). Возьмём x=4 и y=14. (табл. 1)

Таблица 1 – Проверка ПР.

y	y/x	]y/x[	r(x,y)	f=|x-(r(x,y)+1)|	sg(f)	⌐sg(f)	q(x,y)	Состояние
_	_	_	_	—
0,25	Сохранение значения
0,5	Сохранение значения
0,75	Сохранение значения
Переход
1,25	Сохранение значения
1,5	Сохранение значения
1,75	Сохранение значения
Переход
2,25	Сохранение значения
2,5	Сохранение значения
2,75	Сохранение значения
Переход
3,25	Сохранение значения
3,5	Сохранение значения

Конструирование машины Тьюринга

Рисунок 1 – графическое отображение ПРФ

Очевидно, что функция переходит в новое значение в точках, в которых y делится на x без остатка. (Рис.1)

РАЗРАБОТКА ПРОГРАММЫДЛЯ МАШИНЫПОСТА

Идея решения

Идея решения заключается в том, что максимальный порядок постова слова равен 3 и как только количество подряд стоящих пробелов будет больше 3, то это означает, что постово слово закончилось и нужно возвращаться к началу. (Рис.2; рис.3)

Рисунок 2 – Исходное состояние машины Поста

Рисунок 3 – Конечное состояние машины Поста

Составление схем

Процесс проектирования заключается в составлении алгоритмов, которые будут исполняться позже на машине Поста. Основными вспомогательными элементами являются крупная схема алгоритма (рис.4), позволяющая представить метод решения в целом; и детализированная схема алгоритма, отображающая будущий код в доступном восприятию человека схематическом виде (рис.5).

Рисунок 4 – Крупная схема алгоритма

Рисунок 5 – Детализированная схема алгоритма. Лист 1

Написание программы на машине Поста

Результатом написания кода на машине Поста является работающая программа, позволяющая уменьшать порядок постова слова на 1, при условии, что максимальный порядок 3.

Скриншоты работающей программы представлены на рисунках 6-9.

Рисунок 6 – Работающая программа Поста (Снимок 1)

Как запрограммировать на машине Тьюринга сложение? Душкин объяснит

Рисунок 7 – Работающая программа Поста (Снимок 2)

Рисунок 8 – Работающая программа Поста (Снимок 3)

Рисунок 9 – Работающая программа Поста (Снимок 4)

Анализ результата

Полученная программа полностью выполняет поставленную задачу. Программа была написана для постова слова порядка 3. Содержит 21 строку кода.

РАЗРАБОТКА ПРОГРАММЫДЛЯ МАШИНЫТЬЮРИНГА

Идея решения

Идея решения заключается в том, что, начиная с первой буквы моей фамилии, буквы копируются за символ *.

Внешний алфавит машины Тьюринга: A=

Составление ГСП и ТСП

Рисунок 10 – ГСП программы

Таблица 2 – ТСП программы.

QA	г	и	з	т	д	н	о	в	*	λ
q1	q1 г R	q1 и R	q1 з R	q1 т R	q1 д R	q1 н R	q1 о R	q1 в R	_	q2 * R
q2	_	_	_	_	_	_	_	_	_	q3 г L
q3	_	q4 и L	_	q3 т L	_	q3 н L	q3 о L	q3 в L	q3 * L	_
q4	q5 г R	_	q3 з L	_	q3 д L	_	_	_	_	_
q5	q5 г R	q5 и R	q5 з R	q5 т R	q5 д R	q5 н R	q5 о R	q5 в R	q5 * R	q6 и L
q6	q6 г L	q6 и L	q7 з R	q6 т L	q6 д L	q6 н L	q6 о L	q6 в L	q6 * L	_
q7	q7 г R	q7 и R	_	q7 т R	q7 д R	q7 н R	q7 о R	q7 в R	q7 * R	q8 з L
q8	_	q9 и L	_	q8 т L	_	q8 н L	q8 о L	q8 в L	q8 * L	_
q9	q8 г L	_	q10 з R	_	q8 д L	_	_	_	_	_
q10	q10 г R	q10 и R	q10 з R	q10 т R	q10 д R	q10 н R	q10 о R	q10 в R	q10 * R	q11 и L
q11	q11 г L	q11 и L	q11 з L	q12 т R	q11 д L	q11 н L	q11 о L	q11 в L	q11 * L	_
q12	q12 г R	q12 и R	q12 з R	_	q12 д R	q12 н R	q12 о R	q12 в R	q12 * R	q13 т L
q13	q13 г L	q13 и L	q13 з L	_	q14 д R	q13 н L	q13 о L	q13 в L	q13 * L	_
q14	q14 г R	q14 и R	q14 з R	q14 т R	_	q14 н R	q14 о R	q14 в R	q14 * R	q15 д L
q15	_	q16 и L	_	q15 т L	_	q15 н L	q15 о L	q15 в L	q15 * L	_
q16	q15 г L	_	q15 з L	_	q17 д R	_	_	_	_	_
q17	q17 г R	q17 и R	q17 з R	q17 т R	q17 д R	q17 н R	q17 о R	q17 в R	q17 * R	q18 и L
q18	q18 г L	q18 и L	q18 з L	q18 т L	q18 д L	q19 н R	q18 о L	q18 в L	q18 * L	_
q19	q19 г R	q19 и R	q19 з R	q19 т R	q19 д R	_	q19 о R	q19 в R	q19 * R	q20 н L
q20	q20 г L	q20 и L	q20 з L	q20 т L	q20 д L	_	q21 о R	q20 в L	q20 * L	_
q21	q21 г R	q21 и R	q21 з R	q21 т R	q21 д R	q21 н R	_	q21 в R	q21 * R	q22 о L
q22	q22 г L	q22 и L	q22 з L	q22 т L	q22 д L	q22 н L	_	q23 в R	q22 * L	_
q23	q23 г R	q23 и R	q23 з R	q23 т R	q23 д R	q23 н R	q23 о R	_	q23 * R	q24 в L
q24	q24 г L	q24 и L	q24 з L	q24 т L	q24 д L	q24 н L	q24 о L	q24 в L	q24 * L	qz λ R

Написание программы на машине Тьюринга

На рисунках 11 – 12 представлен фрагмент программы с внешним алфавитом машины Тьюринга: A=< ,г,и,з,т,д,*>.

Рисунок 11 – Работающая программа Тьюринга (Снимок 1)

Рисунок 12 – Работающая программа Тьюринга (Снимок 2)

На рисунках 13 – 15 представлена написанная программа по ТСП.

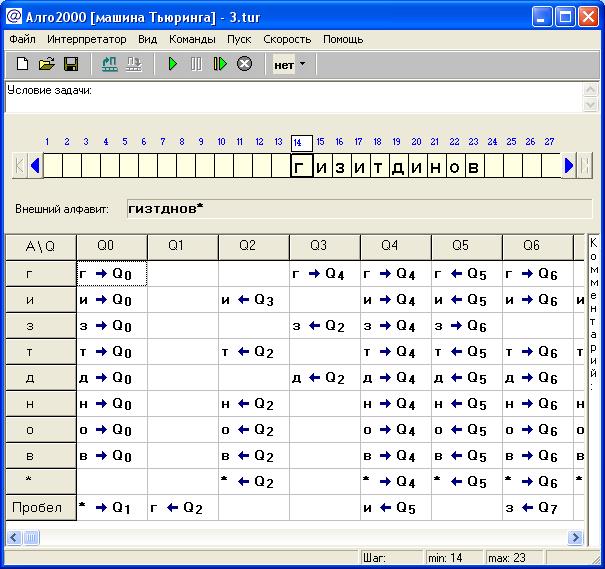
Рисунок 13 – Работающая программа Тьюринга (Снимок 3)

Рисунок 14 – Работающая программа Тьюринга (Снимок 4)

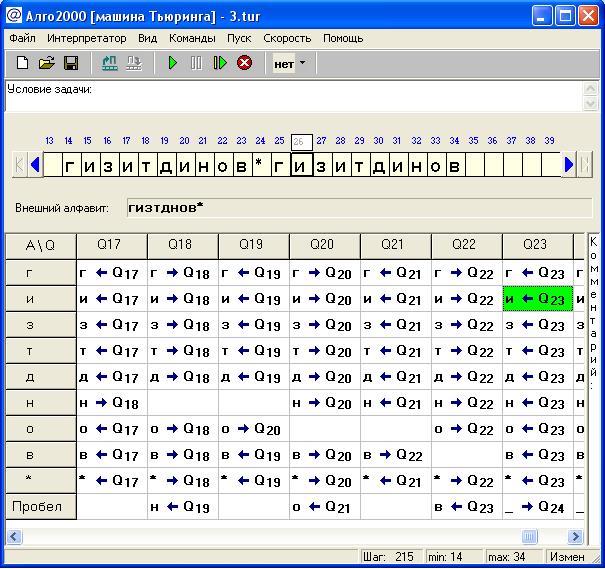
Рисунок 15 – Работающая программа Тьюринга (Снимок 5)

Анализ результата

Написанная программа позволяет скопировать мою фамилию и вернуть каретку в начало. Программа содержит 24 состояния.

ВЫВОД

Была решена задача на примитивную рекурсию, спроектированы и написаны программы: уменьшение порядка постова слова на 1 и копирование своей фамилии на машине Тьюринга.

СПИСОК ЛИТЕРАТУРЫ

1. Ершов, С. С. Элементы теории алгоритмов: учебное пособие/ С. С. Ершов. — Челябинск: Изд-во ЮУрГУ, 2009. — 64 с.

2. Ершов С.С., Надточий И.Л., Самохвалов А.В. Прикладная математика: Учебное пособие по практическим занятиям. – Челябинский ЧТУ, 1992. – 85с.

3. СТО ЮУрГУ 04–2008 Стандарт организации. Курсовое и дипломное проекти-рование. Общие требования к содержанию и оформлению / составители: Т.И. Парубочая, Н.В. Сырейщикова, В.И.

Гузеев, Л.В. Винокурова. – Челябинск: Изд-во ЮУрГУ, 2008. – 56 с.

Источник: poisk-ru.ru

5.3 Реализация машины Тьюринга

Рассмотрим вопрос о реализации машины Тьюринга. Очевидно, что наращиваемую память в современных ЭВМ можно считать аналогом бесконечной в одну сторону рабочей ленты машины Тьюринга. Какого количества и каких команд достаточно, чтобы реализовать операции машины Тьюринга? Очевидно, что для этого достаточно только пяти типов команд:

Сдвиг головки на 1 позицию на ленте влево или вправо

переход,р

Безусловный переход к команде с номером р

если,s,р

Условный переход к команде с номером р, если в обозреваемой ячейке находится символs

печать, s

Печать символа sв обозреваемую ячейку

Например, начало программы машины Тьюринга, которая находит наибольший общий делитель (рис.5.4), имеет вид:

01: переход, 05;

02: печать,а;

03: сдвиг,влево;

04: переход,00;

06:переход, 10;

07:печать,b;

08:сдвиг,влево;

Из этого можно сделать следующий вывод: для того, чтобы автоматическое вычислительное устройство могло реализовать любой алгоритм, достаточно, чтобы оно могло работать с линейной памятью — аналогом полубесконечной входной ленты машины Тьюринга и могло выполнять по крайней мере пять перечисленных выше операций. Известно, что все современные компьютеры включают подобные команды. Это означает, что все они являются универсальными вычислителями. Известно также, что кроме этих команд, компьютеры включают также множество и других видов команд. Очевидно, эти дополнительные командыне расширяютпринципиальновозможностей компьютеров, но существенно повышают удобство и эффективность вычислителей.

Другой интересный вывод связан с возможностью реализации машины Тьюринга на языке высокого уровня. Поставим вопрос: какие управляющие конструкции достаточны для реализации любой машины Тьюринга? Очевидно, что c помощью последовательности операторов, выбора (if-then-else), цикла (while)и перехода(goto) любую программу машины Тьюринга можно реализовать.

Однако, справедливо и более сильное утверждение: оператор перехода в этом наборе лишний. Действительно, пустьstate — переменная типасостояние,symbol — переменная типасимвол. Пусть элементарными операциями языка являютсяЧитать(с)- чтение очередного символа из обозреваемой ячейки входной ленты (или моделирующего ее массива) и помещение его в переменнуюс,Писать(с)- печатать символсв обозреваемую ячейку входной ленты иСдвиг (D)- имитация сдвига головки чтения-записи по рабочей ленте МТ (фактически, изменение индекса читаемого элемента одномерного массива). Очевидно, что любая программа машины Тьюринга может быть построена так:

state = s0; //начальное состояние

while ( state != стоп ) do // повторяем цикл, пока не придем в заключительное состояние

Читать(symbol);

if (state = = s

Сдвиг (D)

if (state = = …

Отсюда следует важный вывод: любую машину Тьюринга (и, следовательно, любой алгоритм) можно реализовать на языке высокого уровня с использованием только трех управляющих конструкций: последовательность, выбор и цикл. Тем самым мы доказали известную основную теорему структурного программирования, доказанную впервые из других соображений Бомом и Якопини.

Источник: studfile.net

Машины Тьюринга в Python

Хотя у вас может не быть доступа к физической машине Тьюринга, это не должно помешать вам смоделировать машину Тьюринга с помощью… вашего компьютера! Я расскажу о том, как работают машины Тьюринга, и о коде Python, чтобы построить простую машину для проверки предполагаемых палиндромов. Я знаю, что программы, которые проверяют палиндромы, являются обычным упражнением для новичков в программировании, и что вы можете просто проверить их в Интернете или даже скопировать код на своем любимом языке. Однако давайте представим, что в глубине души вы действительно хотели бы использовать для этой задачи машину Тьюринга.

Эта статья вдохновлена ​​главой 5 книги Перспективы вычислений Роберта Героха — Amazon.

Что такое машина Тьюринга?

Машина Тьюринга состоит из трех частей:

1. Лента.
2. Пишущая головка
3. Состояние машины.

Лента разделена на последовательность квадратов, в каждом из которых может храниться один символ, принадлежащий к данному набору символов.

Это не очень ответило

Чем интересны машины Тьюринга? Вы определенно уже слышали о них, поэтому давайте просто быстро скопируем это из собственных слов Тьюринга и оставим дальнейшие подробности в главе Героха, упомянутой выше.

Можно изобрести одну машину, которую можно использовать для вычисления любой вычислимой последовательности.

Машина Тьюринга может смоделировать что угодно, имея неограниченное пространство для хранения!

Как работают машины Тьюринга?

Машина работает на основе таблицы правил. На любом заданном шаге записывающая головка находится над каким-то квадратом на ленте. В этот момент машина: (1) считывает этот квадрат ленты и (2) считывает состояние, в котором находится машина. Затем машина просматривает таблицу правил, чтобы определить: (1) какой новый символ нужно записать , (2) в какое новое состояние перейти и (3) в каком направлении, на одну клетку влево или вправо, должна двигаться голова. Конечно, машине разрешено печатать один и тот же символ и сохранять то же состояние.

Когда машина закончила? Для этой цели зарезервировано специальное состояние. Как только машина входит в это состояние, программа завершает работу.

Технически мы сделаем несколько упрощений машины Тьюринга. Во-первых, предположим, что у нас есть постоянный доступ к состоянию машины, и мы можем просто измерить, завершилась она или нет. То есть машине не нужно будет писать на ленте, чтобы указать, что она закончила. Что касается кода, если хотите, игнорируйте неэффективность и сосредоточьтесь на функции.

Реализация машины Тьюринга

Машина Тьюринга состоит из трех элементов (которые мы реализуем следующим образом):

1. состояние (строка с именем state )
2. записывающая головка (целое число с именем write_head )
3. лента (список с именем tape_list )

В качестве простой реализации напишем класс с этими элементами следующим образом:

Далее мы будем работать с таблицей правил, определенной в updateMachine .

Таблица правил

А таблица правил? Таблица, которую необходимо реализовать, приведена ниже — под ней следует пояснение.

Это требует некоторого объяснения! Начнем с определения состояний:

• q1 — исходное состояние. Здесь мы читаем символ n , который соответствует n-му символу в списке символов (при условии, что он не равен нулю). Эта информация «сохраняется» в состоянии при переходе в соответствующее состояние pn .
• pn — состояние после прочтения n-го символа изначально — теперь идем вправо и ищем конец строки, отмеченный нулем.
• rn — состояние после нахождения нуля в конце строки — теперь сравним последний символ строки. Если это палиндром, то он должен быть таким же, как n-й символ, который мы читаем в начале, и мы переходим в состояние q2 . в противном случае перейдите к состоянию qn, что означает «нет, это не палиндром».
• q2 — состояние после успешного сравнения последнего символа в строке — теперь идем влево и ищем начало строки, отмеченное нулем. Перезапустите цикл, перейдя к q1 .

Если вы запутались, некоторые примеры могут прояснить ситуацию. В таблицах ниже мы перечисляем ленту на каждом шаге (где положение записывающей головки подчеркнуто), а также состояние и char.

Во-первых, слово «из», которое не является палиндромом:

В последней строке, поскольку «f» не был 15-м символом алфавита (а именно «o», который мы считывали на первом шаге), машина переходит в состояние qn, правильно указывая, что «of» не является палиндром.

Во-вторых, символы «bbb», которые являются палиндромами:

Это было ужасно долго, но это сработало! Обратите внимание, что для переключения с p2 на r2 во второй раз при чтении нуля использовалось наше дополнительное условие * в таблице правил.

Или, что угодно, это работает.

Что касается кода, опять же, не усложняйте его и используйте операторы if и elif :

Настройка ввода/вывода

Нам по-прежнему нужен способ ввести строку в программу, а также установить начальное состояние машины, начальное положение записывающей головки и записать строку на ленту. Давайте сделаем все это сейчас:

Запуск кода

Наконец, давайте запустим код! Опять же, мы обманули и обращаемся к состоянию на каждой итерации, чтобы проверить, завершилась ли программа (состояние qn или qy). Однако вы легко можете представить себе печать на ленте специального символа для обозначения результата при желании (оставим это как «упражнение»). Создайте файл с именем test.py с содержимым:

Запуск этого дает:

> python test.py hello Checking: hello — — — q1 0 [‘h’, ‘e’, ‘l’, ‘l’, ‘o’, 0] p7 1 [0, ‘e’, ‘l’, ‘l’, ‘o’, 0] p7 2 [0, ‘e’, ‘l’, ‘l’, ‘o’, 0] p7 3 [0, ‘e’, ‘l’, ‘l’, ‘o’, 0] p7 4 [0, ‘e’, ‘l’, ‘l’, ‘o’, 0] p7 5 [0, ‘e’, ‘l’, ‘l’, ‘o’, 0] r7 4 [0, ‘e’, ‘l’, ‘l’, ‘o’, 0] qn 3 [0, ‘e’, ‘l’, ‘l’, ‘o’, 0] — — — hello is NOT a palindrome! Steps: 7
Checking: ooo — — — q1 0 [‘o’, ‘o’, ‘o’, 0] p14 1 [0, ‘o’, ‘o’, 0] p14 2 [0, ‘o’, ‘o’, 0] p14 3 [0, ‘o’, ‘o’, 0] r14 2 [0, ‘o’, ‘o’, 0] q2 1 [0, ‘o’, 0, 0] q2 0 [0, ‘o’, 0, 0] q1 1 [0, ‘o’, 0, 0] p14 2 [0, 0, 0, 0] r14 1 [0, 0, 0, 0] q2 0 [0, 0, 0, 0] q1 1 [0, 0, 0, 0] qy 2 [0, 0, 0, 0] — — — ooo is a palindrome! Steps: 12

Последние мысли

Это определенно был самый утомительный способ проверки палиндромов из когда-либо придуманных! Но волшебство в том, что нет предела тому, что вы можете реализовать с помощью машины Тьюринга, пока на вашем компьютере не закончится память.

Источник: questu.ru