Рассмотрим преобразование целого положительного десятичного числа в двоичную систему счисления.
Программа для перевода десятичного числа в двоичную систему счисления
using System; using System.Text; class Program < static string DecimalToBinary(uint decimalNumber) < var binaryNumber = string.Empty; while (decimalNumber > 0) < binaryNumber = (decimalNumber % 2) + binaryNumber; decimalNumber /= 2; > return binaryNumber; > private static void Main(string[] args) < Console.OutputEncoding = Encoding.UTF8; Console.Write(«Введите число в десятичной системе: «); var decNum = uint.Parse(Console.ReadLine()); var binNum = DecimalToBinary(decNum); Console.WriteLine(» => «, decNum, binNum); Console.ReadLine(); > >
Источник: programm.top
Как перевести число из десятичной системы счисления в двоичную в Python

Из десятичной в двоичную
Введение в перевод чисел в различные системы счисления
Числа в компьютерной науке и программировании представляются в различных системах счисления, таких как двоичная, восьмеричная и шестнадцатеричная. Понимание, как переводить числа из одной системы счисления в другую, является важным навыком при работе с программами и алгоритмами.
Перевод чисел из десятичной системы счисления в другие системы является одной из наиболее распространенных операций. В данной статье мы сосредоточимся на переводе чисел из десятичной системы в двоичную систему счисления.
Десятичная система счисления, или основание 10, является наиболее распространенной системой счисления в повседневной жизни. В ней используются цифры от 0 до 9, а каждая позиция числа имеет вес, увеличивающийся в 10 раз с каждой следующей позицией. Например, число 357 в десятичной системе счисления представляет собой 3 * 10 2 + 5 * 10 1 + 7 * 10 0 .
Двоичная система счисления, или основание 2, использует всего две цифры — 0 и 1. Каждая позиция числа в двоичной системе имеет вес, увеличивающийся в 2 раза с каждой следующей позицией. Например, число 101 в двоичной системе счисления представляет собой 1 * 2 2 + 0 * 2 1 + 1 * 2 0 , что равно 5 в десятичной системе.
Перевод чисел из десятичной системы в двоичную систему может быть полезным при работе с битовыми операциями, компьютерными сетями, шифрованием и другими аспектами программирования.
В следующих разделах мы рассмотрим различные методы и алгоритмы перевода чисел из десятичной системы в двоичную систему счисления. Это поможет нам лучше понять процесс перевода и научиться применять его в наших программных проектах.
Основы двоичной системы счисления
Двоичная система счисления является основой для работы с компьютерами, так как вся информация в компьютерах представлена в виде двоичных чисел — наборов из нулей (0) и единиц (1). В данном разделе мы познакомимся с основами двоичной системы и ее структурой.
Перевод числа из двоичной системы счисления в десятичную
Двоичная система счисления основана на позиционной системе, где каждая позиция числа имеет определенный вес, увеличивающийся вдвое с каждым следующим разрядом. В двоичной системе счисления используются всего две цифры: 0 и 1.
Позиции чисел в двоичной системе называются разрядами. Начиная с самого правого разряда, позиции имеют веса, соответствующие степеням числа 2. Например, в двоичной системе число «101» можно разложить следующим образом: 1 * 2 2 + 0 * 2 1 + 1 * 2 0 = 4 + 0 + 1 = 5.
Когда мы работаем с двоичными числами, мы можем заметить некоторые особенности. Например, число, оканчивающееся на ноль, всегда будет кратным 2. Каждый разряд числа может быть либо нулем, либо единицей. При увеличении числа на единицу в двоичной системе, мы изменяем только самый правый разряд. Если все разряды числа равны единице и мы добавляем единицу, то получим новое число, состоящее из всех нулей с одной единицей в более старшем разряде. Это называется переполнением.
Понимание основ двоичной системы счисления важно при работе с компьютерами и программированием. Оно помогает нам понять внутреннее представление данных, выполнение битовых операций, работу с памятью и другие аспекты компьютерной науки.
Математический подход к переводу числа из десятичной системы в двоичную
Перевод числа из десятичной системы счисления в двоичную можно выполнить с помощью математического подхода. Этот метод основан на последовательном делении числа на 2 и записи остатков в обратном порядке.
Вот шаги для перевода числа из десятичной системы в двоичную с использованием математического подхода:
- Начните с десятичного числа, которое вы хотите перевести в двоичную систему.
- Разделите это число на 2 и запишите остаток.
- Результат деления становится новым числом, и процесс повторяется до тех пор, пока результат деления не станет равным нулю.
- Запишите остатки от каждого деления в обратном порядке. Это будет двоичное представление исходного числа.
Давайте рассмотрим пример для наглядности. Переведем число 25 из десятичной системы в двоичную:
- Шаг 1: 25 / 2 = 12 с остатком 1
- Шаг 2: 12 / 2 = 6 с остатком 0
- Шаг 3: 6 / 2 = 3 с остатком 0
- Шаг 4: 3 / 2 = 1 с остатком 1
- Шаг 5: 1 / 2 = 0 с остатком 1
Теперь запишем остатки в обратном порядке: 11001. Полученное число 11001 является двоичным представлением числа 25.
В Python можно использовать цикл и операторы деления и остатка для реализации этого математического подхода. Мы также можем использовать строковые операции для записи остатков и получения окончательного двоичного числа.
Математический подход к переводу чисел из десятичной системы в двоичную является фундаментальным и полезным при работе с двоичными данными. Он может быть расширен для перевода чисел в другие системы счисления, такие как восьмеричная или шестнадцатеричная, и помогает понять внутреннее представление чисел в компьютерных системах.
Использование встроенных функций Python для перевода чисел в двоичную систему
Python предоставляет удобные встроенные функции для выполнения преобразований чисел из десятичной системы счисления в двоичную. Эти функции позволяют нам легко и эффективно выполнять перевод без необходимости реализации алгоритма вручную.
Функция bin()
Функция bin() используется для получения двоичного представления числа в виде строки. Она принимает десятичное число в качестве аргумента и возвращает его двоичное представление. Например:
decimal_num = 25 binary_num = bin(decimal_num) print(binary_num) # ‘0b11001’
Обратите внимание, что результатом будет строка, начинающаяся с префикса ‘0b’, который указывает на двоичное представление.
Метод format()
Метод format() может использоваться для форматирования числа в двоичную систему счисления. Он позволяет задавать формат числа, включая систему счисления. Для перевода числа в двоичную систему счисления мы можем использовать формат ‘b’. Пример использования метода format() для перевода числа в двоичную систему:
decimal_num = 25 binary_num = format(decimal_num, ‘b’) print(binary_num) # ‘11001’
Здесь мы передаем десятичное число и формат ‘b’ в качестве аргументов метода format(), что приводит к его представлению в двоичной системе счисления.
Оба этих подхода предоставляют удобные и простые способы перевода чисел из десятичной системы в двоичную в Python. Выбор конкретного метода зависит от ваших предпочтений и требований конкретной задачи.
Ручная реализация алгоритма перевода в двоичную систему в Python
Перевод числа из десятичной системы счисления в двоичную можно выполнить вручную, следуя простому алгоритму. Алгоритм основан на делении числа на 2 и записи остатков в обратном порядке.
- Инициализируйте пустую строку (или список) для записи двоичного представления числа.
- Делите исходное число на 2 и запоминайте остаток от деления.
- Делите полученное частное на 2 и снова запоминайте остаток.
- Продолжайте делить полученные частные на 2 и запоминать остатки до тех пор, пока частное не станет равным 0.
- Запишите все запомненные остатки в обратном порядке — это будет двоичное представление числа.
Пример реализации алгоритма в Python:
decimal_num = 42 binary = «» while decimal_num > 0: remainder = decimal_num % 2 binary = str(remainder) + binary decimal_num = decimal_num // 2 print(binary)
В этом примере мы выполняем перевод числа 42 из десятичной системы в двоичную. Мы инициализируем пустую строку binary для записи двоичного представления числа. Затем мы выполняем деление числа на 2 и запоминаем остаток. Полученный остаток добавляем в начало строки binary . Затем мы делим частное на 2 и повторяем процесс до тех пор, пока частное не станет равным 0. Наконец, мы выводим полученное двоичное представление числа.
Ручная реализация алгоритма позволяет нам лучше понять процесс перевода чисел в двоичную систему и может быть полезна при работе с другими системами счисления или при необходимости настроить алгоритм под специфические требования.
Источник: python-teach.ru
Перевод из десятичной системы счисления в двоичную
Перед тем как перейти к алгоритму перевода, вспомним алфавит двоичной и десятичной системы счисления:
Для перевода чисел из десятичной системы в двоичную, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.
Алгоритм перевода целых десятичных чисел в двоичную систему счисления
- Последовательно выполнять деление десятичного числа и получаемых целых частных на 2, до тех пор, пока частное не станет равным 0.
- Для получения ответа в двоичном коде, необходимо записать, полученные, в результате деления остатки, в обратном порядке.
Пример 1 : перевести десятичное число 123 в двоичную систему счисления
Для наглядности произведем деление «столбиком». Решение будет выглядеть следующим образом:
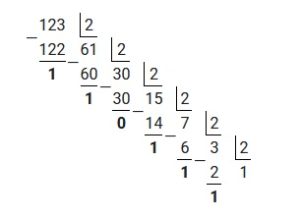
Исходя из вышеприведенного алгоритма, полученные остатки необходимо записать в обратном порядке.
Алгоритм перевода десятичной дроби в двоичную систему
- Последовательно выполнять умножение исходной дроби на 2, до тех пор, пока, дробная часть не станет равна 0 или пока не будет достигнута необходимая точность вычисления.
- Полученная дробь в двоичной системе будет равна прямой последовательности целых частей произведений.
Пример 2: перевести число 0,123 в двоичную систему.
Решение будет выглядеть следующим образом:
0.123 ∙ 2 = 0.246 (0)
0.246 ∙ 2 = 0.492 (0)
0.492 ∙ 2 = 0.984 (0)
0.984 ∙ 2 = 1.968 (1)
0.968 ∙ 2 = 1.936 (1)
0.936 ∙ 2 = 1.872 (1)
0.872 ∙ 2 = 1.744 (1)
0.744 ∙ 2 = 1.488 (1)
0.488 ∙ 2 = 0.976 (0)
0.976 ∙ 2 = 1.952 (1)
0.952 ∙ 2 = 1.904 (1)
В данном примере можно продолжить вычисления, но зачастую, такой точности будет достаточно.
Перевод дробного десятичного числа в двоичную систему
Для того чтобы перевести десятичное число, содержащее дробную часть, необходимо отдельно перевести целую часть и отдельно дробную.
Пример 3: перевести число 110,625 из десятичной системы в двоичную
Для решения примера потребуется отдельно перевести 110 и отдельно 0,625 из десятичной системы в двоичную, используя вышеизложенные алгоритмы. Таким образом переведя 110, получим:
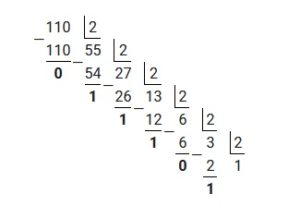
Перевод десятичной дроби 0,625 выглядит так:
0.625 ∙ 2 = 1.25 (1)
0.25 ∙ 2 = 0.5 (0)
0.5 ∙ 2 = 1 (1)
Теперь осталось соединить результаты перевода. Таким образом: 110.62510=1101110.1012
Обратите внимание, что данный пример наглядно демонстрирует ситуацию, при которой дробная часть стала равной 0 и дальнейшее вычисление закончилось.
Источник: sistemy-schisleniya.ru