— средняя наработка программы на отказ T , являющаяся математическим ожиданием временного интервала между последовательными отказами. При определении характеристик надежности ПО учитывается тот факт, что возникающие при работе программ ошибки устраняются, количество ошибок уменьшается и, следовательно, их интенсивность понижается, а наработка на отказ программы увеличивается. В связи с такими предположениями рассматривается несколько моделей надежности ПО: модель с дискретно-понижающей частотой появления ошибок, модель с дискретным увеличением наработки на отказ или ошибку ПО, экспоненциальная модель надежности ПО.
Модель с дискретно-понижающей частотой появления ошибок ПО
В этой модели предполагается, что интенсивность отказов программы λ(t) является постоянной величиной до обнаружения возникшей ошибки и, как следствие – отказа программы и ее устранения. После этого значение λ(t) уменьшается и интенсивность отказов снова становится константой. В этой модели предполагается, что между λ(t) и числом оставшихся в программе ошибок существует зависимость
Вероятность работы цепи.Гирлянда
λ (t) = K(M — i) = λi , где M – неизвестное первоначальное число ошибок;
i – число обнаруженных ошибок, зависящее от времени t; K – некоторая константа.
Характер изменения интенсивности отказов для этой модели представлен
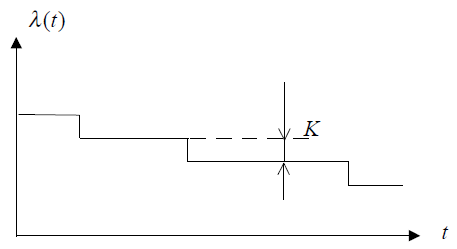
Характер изменения интенсивности отказов программы от времени наработки при модели с дискретно-понижающей частотой появления ошибок
Плотность распределения времени обнаружения i-й ошибки ti определяется соотношением
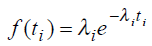
Значения неизвестных параметров K и M могут быть оценены на основании последовательности наблюдения интервалов между моментами обнаружения ошибок.
На практике условия рассмотренной модели нередко не соблюдаются, а именно:
— не всегда при устранении ошибки интенсивность отказов уменьшается на одну и ту же величину K , так как разные ошибки имеют различное влияние на ход исполнения программы;
— довольно часто возникают ситуации, при которых устранение одних ошибок приводит к появлению новых;
— не всегда удается устранить причину ошибки и программу продолжают использовать, так как при других исходных данных ошибка может себя и не проявить.
15 Модель с дискретным увеличением времени наработки на отказ по. Экспоненциальная модель надежности по
Основным допущением в этой модели является предположение о том, что отказы и ошибки программы в начале эксплуатации возникают часто. По мере отладки программы таких ошибок становится меньше, а время наработки на отказ после ликвидации очередного отказа увеличивается
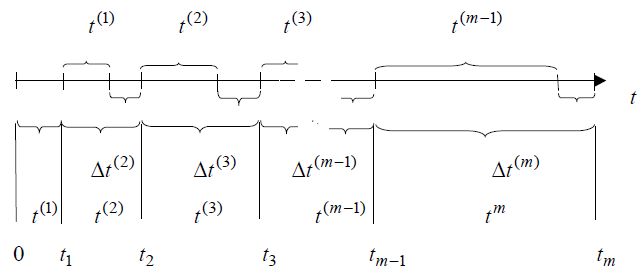
Диаграмма интервалов времени наработки на отказ компьютерной программы
На диаграмме величины t1, t2, t3,…, tm-1, tm – случайные моменты времени возникновения первого, второго, третьего и так далее – m-го отказов. Величины t (1) , t (2) , t (3) ,…, t(m-1) , t(m) – случайные интервалы времени между соседними отказами программы (обозначены под первым рядом нижних скобок диаграммы). Интервалы Δt(2) , Δt(3) , Δ t(m-1) , Δ t(m) также являются случайными временными интервалами.
Практическая работа №1. Колич. характ. надежности Вероятность безотказной работы, вероятность отказа
Пусть первая ошибка, проявившаяся в результате отказа программы, произошла в случайный момент времени t1 и была устранена. Наработка до первого отказа и возникшей ошибки равна интервалу времени t (1) . Вторая ошибка возникла в момент времени t2 . Наработка до второй ошибки определяется интервалом t(2) . В соответствии с предположением, этот интервал больше, чем t (1) , так как после перезапуска программа проработала время до первой ликвидированной ошибки, продолжила работу до новой, второй ошибки. Следовательно, интервал t (2) можно представить в виде
t (2) = t (1) + Δt (2) , где Δ t(2) – дополнение интервала t(1) до величины интервала t(2).
Обобщая эти рассуждения до любого i -го интервала (i =1,m), можно записать
t(i) = t(i-1) + Δ t(i) .
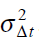
Случайные величины Δ t(i) являются независимыми, имеют математическое ожидание M[Δ t] и дисперсию
Случайное время возникновения (i -1) ошибки ti отсчитывается от начального момента времени t0 = 0. Время, необходимое на ликвидацию ошибки, в расчет не берется. В этом случае для всех случайных моментов времени возникновения ошибки и временных интервалов между соседними ошибками можно записать:
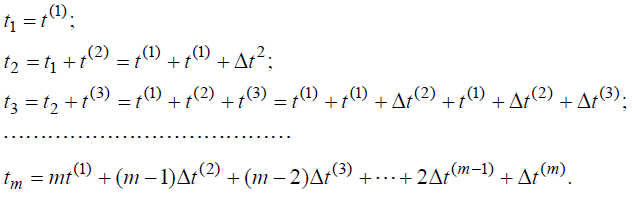
Учитывая, что от момента времени t0 = 0 до начала момента t1 не выявлено ни одной ошибки программы и в силу того, что интервал t (1) сравнительно невелик, так как ошибки программы вначале ее эксплуатации происходят довольно часто, можно представить интервал t (1) как Δ t (1) . Тогда, с учетом этой замены, выражение для tm примет вид
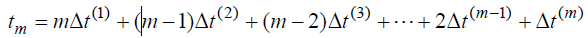
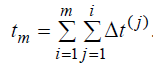
Рассмотрим выражение для t ( i ) при i =1. Согласно ранее принятой замене t (1) на Δt (1) , получим t (1) = t (0) + Δt (1) = Δt (1) .
Действительно, интервал t (0) равен нулю, так как до начала эксплуатации программы никаких ее отказов произойти не могло. Поэтому для любого i = m при i >1 можно записать
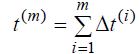
Но t ( m ) – это наработка между (m -1) и m – отказами. Тогда, для любых m, средняя наработка между (m -1) и m отказами равна математическому ожиданию интервала t ( m ) :
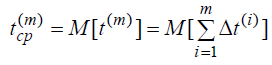
Но для любого i
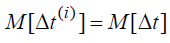Поэтому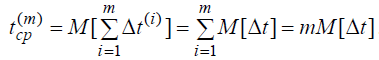 
Отсюда видно, что с увеличением m увеличивается и средняя наработка между двумя отказами.
Рассмотрим среднюю наработку до возникновения m-го отказа. Она равна математическому ожиданию от tm :
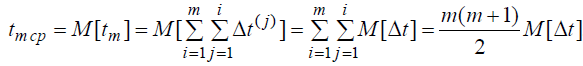
Как и предыдущем случае, из полученного выражения видно, что средняя наработка до отказа возрастает с увеличением числа отказов
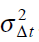
Оценки M[Δt] и получаются по данным об отказах программы в течение периода наблюденияtн :
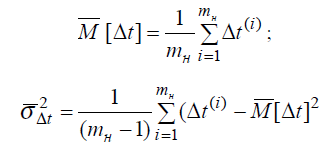
где mн – число отказов за интервал времени (0, tн).
Экспоненциальная модель надежности ПО
Основным предположением этой модели является экспоненциальный характер изменения числа ошибок в программе во времени. Прогноз надежности программы производится на основании данных, получаемых во время ее тестирования.
Основными параметрами модели являются:
— t – суммарное время функционирования от начала тестирования (с устранением обнаруженных ошибок) до момента оценки надежности;
— M – число ошибок, имеющихся в программе перед началом тестирования;
— m(t) – конечное число исправленных ошибок;
— m0(t) – число оставшихся ошибок.
Предполагается, что число ошибок в программе в каждый момент времени имеет пуассоновское распределение, а временной интервал между двумя ошибками распределен по экспоненциальному закону. Параметр этого распределения изменяется после распределения очередной ошибки. Интенсивность отказов считается непрерывной функцией, пропорциональной числу оставшихся ошибок. С учетом введенных параметров и предположений очевидно, что
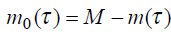а интенсивность ошибок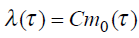 
где C – коэффициент пропорциональности, учитывающий быстродействие ЭВМ и число команд в программе.
Пусть в процессе исправления ошибок новые ошибки не появляются. Следовательно, интенсивность исправления ошибок будет равна интенсивности их обнаружения:
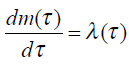
Совместное решение полученных выражений дает
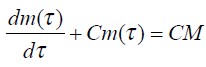
Решением этого уравнения является выражение
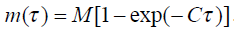
Будем характеризовать надежность программы после тестирования в течение времени τ средним временем наработки на отказ:
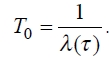Следовательно,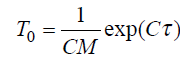 
Введем величину T0т – исходное значение среднего времени наработки на отказ перед тестированием, которое равно
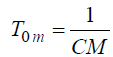
Подставляя это значение в выражение T0 , получим
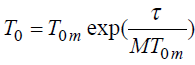
Из этого выражения видно, что среднее время наработки на отказ увеличивается по мере выявления и исправления ошибок.
Таким образом, аналитические модели надежности дают возможность исследовать закономерности проявления ошибок в программе и прогнозировать надежность при ее разработке и эксплуатации.
Источник: studfile.net
Расчёт надёжности программного приложения
Надёжность функционирования ЭС складывается из надёжности аппаратных средств, при помощи которых реализуется программный код, надежности программного приложения (ПП) и качества работы пользователя. ЭС — это сложные системы, включающие в свой состав технические средства, программное обеспечение и часто эргатические (человеко-машинные) звенья. Это можно представить в виде следующей структуры, изображенной на рисунке?
Рисунок? – Схема надёжности функционирования ИС
Исходя из этого, надёжность ЭС будет равна [1]:
,
где — вероятности безотказной работы аппаратных средств;
— вероятности безотказной работы программного приложения;
— вероятности безотказной работы человека-оператора (системного оператора).
Надежность работы ПП зависит от надежности работы аппаратной части (технических средств) и программного обеспечения компьютера. В этом случае обобщающим показателем надежности работы ПП может быть вероятность отсутствия сбоев технических средств и программного обеспечения в течении времени t. Считая независимыми сбои технических средств и программного обеспечения, величину можно определить как:
Пусть система состоит из n элементов, каждый из которых имеет определенные характеристики надежности Pi(t), Qi(t), λi(t), ti (средняя наработка до отказа). Если аналогичные показатели надежности системы обозначить через P(t), Q(t), λ(t) и t, то получаться следующие расчетные зависимости.
На рисунке? приведён расчёт вероятности безотказной работы ПК без резервирования для конфигурации
Рисунок? — Конфигурация компьютера
В соответствии со схемой вероятностей безотказной работы всех его составляющих можно рассчитать по формуле [1]:
, где
N — количество компонентов.
Pi -вероятность безотказной работы i-го компонента.
Вероятность безотказной работы системы с раздельным резервированием определяется по формуле [1]:
, где
— вероятность безотказной работы i-го элемента.
— интенсивность отказов элементов i-го типа
m — количество резервных элементов.
Т — время работы ПК.
Для элементов, используемых в ПК, приняты следующие интенсивности отказов:
Процессор (1): 2.5×10 -7 ч -1
Материнская плата (2): 4.4×10 -7 ч. -1
Память (3): 4.0×10 -7 ч -1
CD-ROM (4): 2.1×10 -7 ч -1
Жесткий диск (5): 7.8×10 -7 ч -1
Контроллер RAID (6): 3.0×10 -7 ч -1
Дисковод (7): 5.0×10 -7 ч -1
Блок питания (8): 1.0×10 -7 ч -1
Сетевая карта (9): 2.0×10 -6 ч -1
Суммарная интенсивность отказов всех устройств:
λобщ =1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 2,5×10 -7 + 4.4×10 -7 + 4.0×10 -7 + 2.1×10 -7 + 7.8×10 -7 + 3.0×10 -7 +5.0×10 -7 + 1.0×10 -6 + 2.0×10 -7 = 4,8х10 -6
Вероятность безотказной работы ПК за Т = 1000 часов:
Предполагается, что система будет работать при наличии рабочей станции, принтера. Структурная схема надёжности информационной сети представлена на рисунке?.
Рисунок? — Схема надёжности
Вероятность безотказной работы компонентов:
Компьютер (РК) – 0,951;
Принтер (РПР) – 0,954.
Расчет вероятности безотказной работы системы вычисляется по формуле:
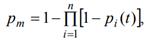
где n – количество элементов.
Так как сеть одноранговая, то
Для невосстанавливаемых программных средств характеристикой надёжности является вероятность безотказной работы P(t), характеризующая вероятность того, что за время работы t не произойдет отказа программы [1]:
где T — время работы ПО до отказа или наработка до отказа (T — случайная величина);
q(t) — вероятность отказа ПО.
Для экспоненциального закона распределения отказов [1]:
,
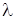
— интенсивность отказов;
t — время работы ПО.
Интенсивность отказов, взяв приемлемой для разрабатываемой системы одну ошибку на 1000 часов работы, можно рассчитать по формуле:
Вероятность безотказной работы подчиняется экспоненциальному закону распределения, можно рассчитать значение вероятности безотказной работы программной части системы за время работы 100 часов (среднее время работы ПО за месяц) [1]:
Расчет надежности системы
Разрабатываемая система в конечном варианте будет представлять собой автоматизированную информационную систему. Таким образом, для обеспечения надежной работы системы необходимо обеспечить надежную работу программной части. При этом надежность системы будет рассчитываться по формуле:
где Рсист — надежность всей системы;
Рапп.ч — надежность аппаратной части;
Рпрог.ч — надежность программной части.
Расчет надежности программной части
Надежность программной части будет рассчитываться по формуле (2):
Где Р оболочка — надежность программного обеспечения оболочки
РПО — надежность разработанного программного обеспечения.
Расчет надежности программного обеспечения оболочки
Надежность программного обеспечения рассчитывается по формуле (4):
Где РОС — надежность операционной системы, установленной на ПК;
РВБ — надежность ПО для работы с приложением.
В качестве операционной системы, используется Windows 10, компания производитель Microsoft Corporation установила вероятность безотказной работы равной:
Для пакета Delphi 7, компания производитель установила вероятность безотказной работы равной:
Вероятность безотказной работы программного обеспечения составляет:
Роболочка = 0,95 * 0,9 = 0,855
Надежность работы системы во многом зависит от безошибочности действия человека-оператора, управляющего системой. В качестве показателя безошибочности часто используют интенсивность ошибок. Безошибочность человека-оператора определяется вероятностью безошибочной работы, которая вычисляется на уровне отдельной операции и на уровне алгоритма [1]:
Pi
где Pi- вероятность безошибочного выполнения операции i-того типа,
Ni — общее число выполненных операций i-го типа,
ni — число допущенных ошибок при выполнении этих операций?
λi — интенсивность ошибок i-го вида,
Ti — среднее время выполнения операций i-го вида.
При работе с информационной системой пользователь осуществляет следующие виды операций:
— выбор правильного ответа при тренинге и экзамене;
Количество выбранных ответов равно общему числу данных в системе. В системе 2 главных блока. Первый блок тренинг в нем 3 раздела, в каждом разделе по 50 вопросов. Второй блок экзамен в нем 100 вопросов. Общая количество вопросов в системе 250.
Таким образом, если ученик решает по 50 вопросов в день, также повторяет пройденный материал и искать материал, то общее количество операций за день равно 200. Предположительно, что ученик допустит минимум 1 ошибку
Исходя из этого, можно рассчитать вероятность безошибочной работы человека – оператора:
Вероятность безотказной работы человека-оператора будет равна:
Исходя из приведённых расчётов, надежность ЭС в целом будет равна [1]:
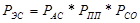
= 0,999*0,855*0,8712 = 0,745
Итоговый показатель вероятности безотказной работы всей системы в целом относительно высок, что говорит о высокой надёжности системы
Источник: poisk-ru.ru
Надёжность программного обеспечения. Введение
Надёжность программного обеспечения — загадочное и неуловимое нечто. Если вы попытаетесь найти что-то по этой теме в яндексе, вы увидите кучу теоретических статей, где написано множество умных слов и формул, но ни одна статья не содержит ни единого примера реального расчёта надёжности программы.
На предприятиях космической отрасли ситуация ещё лучше. Когда я спросил у специалистов одного уральского НПО, как они считают надёжность программного обеспечения, они сделали круглые глаза и сказали: «А чё там, за единицу берём да и всё. А надёжность обеспечиваем отработкой». Я согласен, что такой подход имеет право на жизнь, однако хотелось бы большего.
Короче, я написал свою методику, прошу любить и жаловать. Внизу привожу калькулятор, на котором можно посчитать надёжность этого вашего ПО.
Проблема надёжности программного обеспечения приобретает все большее значение в связи с постоянным усложнением разрабатываемых систем, расширением круга задач, возлагаемых на них, а, следовательно, и значительным увеличением объемов и сложности ПО. Короче, мы дожили до того дня, когда железо стало надёжнее софта, и одна ошибка в программном коде может угробить космическую миссию ценой в миллиарды долларов.
По факту, пообщавшись с коллегами по надёжности и функциональной безопасности, мы коллективно пришли к выводу, что оценивать ВБР (вероятность безотказной работы) ПО не имеет смысла. ПО это тот объект, для которого малоприменимы хорошо отработанные методики оценки надёжности, используемые при оценке компонентов, агрегатов и систем.
Всё, что мы сейчас можем, это открыть неплохой ГОСТ Р 51904-2002 Программное обеспечение встроенных систем. Общие требования к разработке и документированию и выбрать уровень разработки нашего ПО. Самое высоконадёжное (и самое дорогое) ПО будет уровня А, затем B и так далее. Все, что написано ниже — моя творческая инициатива, позволяющая оценить ВБР ПО.
Надёжность программного обеспечения обуславливается наличием в программах разного рода ошибок, внесенных в неё, как правило, при разработке. Под надёжностью ПО будем понимать способность выполнять заданные функции, сохраняя во времени значения установленных эксплуатационных показателей в заданных пределах, соответствующих заданным режимам и условиям исполнения. Под ошибкой понимают всякое невыполнение программой заданных функций. Проявление ошибки является отказом программы.
Показатели надёжности ПО
Наиболее распространенными показателями надёжности ПО являются следующие:
– начальное число ошибок N0 в ПО после сборки программы и перед её отладкой;
– число ошибок n в ПО, обнаруженных и оставшихся после каждого этапа отладки;
– наработка на отказ (MTBF), часов;
– вероятность безотказной работы (ВБР) ПО за заданное время работы P(t);
– интенсивность отказов ПО λ, 10-6 1/ч.
Упрощенная оценка надёжности ПО
Сперва рассмотрим методики, которые предлагаем нам отечественная нормативная база. Единственный нормативный документ по данной теме это ГОСТ 28195-99.
Оценка надежности ПО по ГОСТ 28195-99 рассчитывается по весьма упрощенной методике, констатирующей фактическую надёжность по опыту эксплуатации программного комплекса P(t) 1-n/N, где n – число отказов при испытаниях ПО; N – число экспериментов при испытаниях. Очевидно, что посчитать по этой методике ничего нельзя.
Статистическая оценка надёжности ПО
Куда больший интерес представляет описанная в [1] среднестатистическая оценка начального числа N0 ошибок в ПО после автономной отладки. Согласно данной оценке, количество ошибок на 1 К слов кода составляет 4,34 для языков низкого уровня (Ассемблер) и 1,44 для языков высокого уровня (С++). К сожалению, не совсем понятно, что имели в виду авторы под фразой «1 К слов кода».
В англоязычной литературе принято использовать параметр тысяча строк кода (ТСК) (KLOC). Так, согласно [3] для операционной системы Windows 2000 плотность ошибок составляет 1,8-2,2 на ТСК. Учитывая, что Windows 2000 написан на языке программирования C и имеет близкую размерность числа ошибок, можно с высокой долей достоверности предположить, что отечественный авторы имели в виду именно параметр ТСК.
Отечественные авторы в [1] приводят статистические показатели интенсивности отказов ПО λ. Приведём их в таблице 1.1.
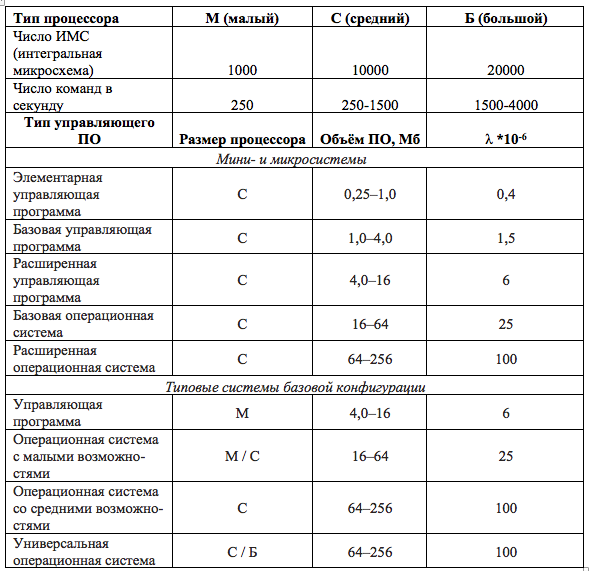
Таблица 1.1
К сожалению, для какого языка ПО это действительно, авторы не сказывают. Кроме того, вводятся поправочные коэффициенты:
Таблица 1.2
И коэффициент, отражающий влияние времени работы программы:
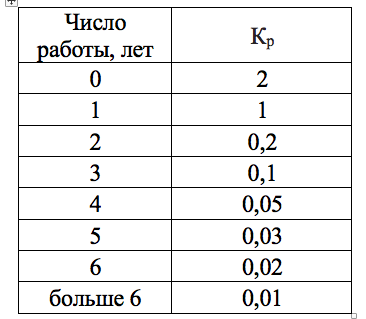
Таблица 1.3
Тогда интенсивность отказов ПО λ определяется с помощью таблиц 1.1-1.3 по выражению:
λ по = λ* Кр* Кк* Кз* Ки (1.1)
Пример расчёта 1.
Объем ПО составляет 1 Мб, например.
Тогда, согласно таблице 1.1 λ = 6
Используем усредненные поправочные коэффициенты. Пусть:
Кр = 2 (короткий срок использования ПО)
Кк = 0,25 (высокое качество ПО)
Кз = 0,25 (высокая частота изменений ПО)
Ки = 1 (уровень загруженности средний)
λ по = 0,1 * 10 -6 отказов/час
Далее, используя экспоненциальную модель надёжности (при использовании данной модели поток отказов считается постоянным), можно получить ВБР ПО по стандартной формуле надёжности:
Данная статистическая модель оценки надёжности ПО обладает значительными достоинствами по сравнению с упрощенной, однако и обладает рядом серьезных недостатков, в частности, она не учитываем язык разработки ПО и имеет большие интервалы объема ПО. То есть нельзя, например, сказать, какая будет надёжность у программы объёмом 2 гига и которая должна работать 10 лет.
Кроме того, поправочные коэффициенты имеют субъективную оценку. С какого потолка они взяты — неизвестно.
Попыткой устранения данных недостатков является Количественная модель оценки надёжности ПО.
Количественная модель оценки надёжности ПО
В основе данной модели лежит моё предположение, что уровень надежности ПО зависит от объема ПО (в битах или тысячах строк кода). Это утверждение не противоречит классической теории надежности, согласно которой чем объект сложнее, тем ниже его надёжность. Логично же. Чем больше будет строк кода, тем больше в итоге будет ошибок и тем ниже будет вероятность безотказной работы программы.
Используем оценку количества ошибок в зависимости от языка разработки из статистической модели:
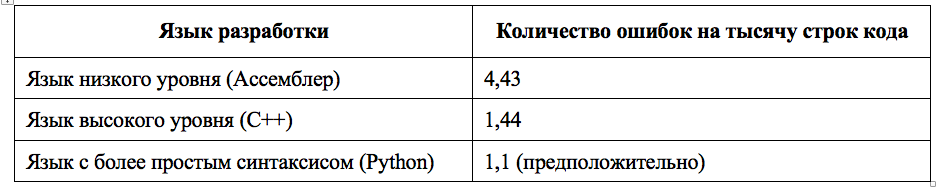
Далее, из [3] взята статистическая оценка связи количества строк кода и битов.
Для языка C, согласно [3] одна строка кода содержит 17 ± 3 байтов (146 битов) информации.
Зная V, объём кода ПО, в битах, мы можем получить число строк этого кода. Удобнее использовать параметр ТСК.
ТСК = V/146000 (1.3)
Используя данные таблицы 1.4 можно получить β, коэффициент количества ошибок на тысячу строк кода:
β = 1,44*ТСК/1000 (1.4)
Объем ПО составляет 10 Мб. Язык разработки С++.
Тогда, согласно 1.3-1.4, β составит 0,08
Данный показатель очень близок к результату Примера 1.
Так появилась идея сопоставить параметр λ — интенсивности отказов ПО, получаемые статистической моделью и β, коэффициент количества ошибок ПО.
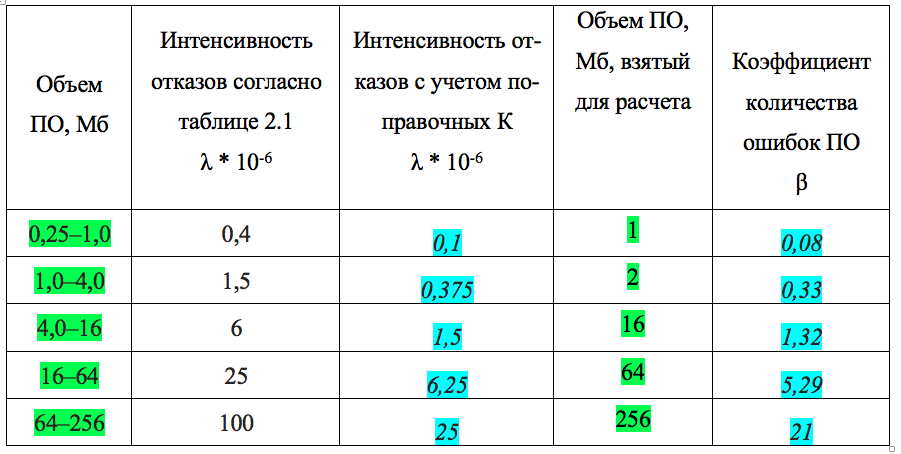
Сейчас внимание! Как видим, есть сильная корреляция результатов между интенсивностью отказов ПО с учётом поправочных коэффициентов и β — коэффициентом количества ошибок ПО. Использование других поправочных коэффициентов приводит к схожим результатам.
Можно сделать предположение, что введенный нами (придуманный мной) β по физическому смыслу близок к λ, интенсивности отказов. λ характеризует частоту отказов. β характеризует частоту ошибок в программе, а значит и отказов. Но! λ и β различаются. λ, единожды определённый для транзистора не изменяется от количества транзисторов. β — коэффициент динамический. Чем больше объём программы, тем больше β. Но это и логично. Чем больше программа, тем в ней больше ошибок. Кроме того, можно предположить, что авторы таблицы 1.1 написали её для ПО на языке С.
Очевидно, чем дольше работает программа, тем выше вероятность, что она откажет.
Используя экспоненциальную модель надёжности (при использовании данной модели поток отказов считается постоянным), можно получить ВБР ПО:
Резюмируя, для того чтобы оценить надёжность программного обеспечения, необходимо знать его язык разработки (высокий или низкий) и объём кода ПО.
[1] Надёжность авиационных приборов и измерительно-вычислительных комплексов, В.Ю. Чернов/ В.Г. Никитин; Иванов Ю.П. – М. 2004.
[2] Надёжность и эффективность в технике: Справочник., В.С. Авдуевский. 1988.
[3] Estimating source lines of code from object code, L. Hatton. 2005.
Попробуйте теперь что-нибудь посчитать. Например, найдите надёжность программного обеспечения, объём которого 100 Мб, и которое должно проработать 100 часов. Важно! Обратите внимание, что λ при изменении объёма ПО каждый раз пересчитывается под конкретный размер ПО.
Валидация модели. Согласно этому сайту надёжность (вероятность безотказной работы) Windows 7 Home Premium составляет 0.98. Правда неизвестно, для какого времени работы сделан расчёт.
Давайте посчитаем по калькулятору. Windows 7 Home Premium после установки занимает около 15 гигабайт или 15360 мегабайт. Примем время работы — большой рабочий день = 12 часов. Тогда ВБР по калькулятору составит 0.984. Неплохо?
Если вы хотите заказать у меня расчет надежности — нажмите на эту ссылку или на кнопку ниже.
