Во многих работах описывающих те или иные алгоритмы, часто можно встретить обозначения типа:
O(g(n)) – Big O – определяет верхнюю границу для работы алгоритма (свободная верхняя граница). Функция описывает зависимость между входными параметрами и кол-вом операций которые придется выполнить.
Ω(g(n))– Big Ω(Omega) используется для описания по нижней границе работы алгоритма. (свободная нижняя граница)
Θ(g(n)) — Big-Θ (Theta) – используется для определения как верхней так и нижней границы работы алгоритма (строгая верхняя и нижняя границы)
Для чего нужна нотация BIG O
Big O нотация нужна для описания сложности алгоритмов. Тут важно понимать, что мы оцениваем время выполнения лишь косвенно, потому что на разном окружение один и тот же код может выполняться разное время. Понимание этой нотации нужно чтобы научиться видеть и исправлять не оптимальный код.
«O» большое и «o» малое — математические обозначения для сравнения асимптотического поведения функций. Используются в различных разделах математики, но активнее всего — в математическом анализе, теории чисел и комбинаторике, а также в информатике и теории алгоритмов.
Как посчитать сложность алгоритма по BIG O | Самое понятное объяснение!
Асимптотическая сложность алгоритмов представляет собой время и память, которые понадобятся вашей программе в процессе выполнения.
Основные допущения
Для оценки в качестве N используется бесконечность
Все константы не влияющие на «бесконечность» будут отброшены. Например, алгоритмы описываемые как O(2*N) и O(N+100) и даже O(N + logN) — это все равно O(N).
При этом если алгоритм имеет несколько неизвестных влияющих на сложность например, O(N+M) – M мы не можем отбросить, потому, что мы о нем ничего не знаем и оно может быть так же равно бесконечности (быть больше N).
Основные классы сложности применяемые при анализе
f(n) = O(1) константа
f(n) = O(log(n)) логарифмический рост
f(n) = O(n) линейный рост
f(n) = O(n*log(n)) квазилинейный рост
f(n) = O(n^m) полиномиальный рост
f(n) = O(2^n) экспоненциальный рост
Источник: dzen.ru
Оценка сложности алгоритмов
В своей деятельности разработчикам практически ежедневно необходимо разрабатывать алгоритмы различного назначения, которые работают с разным набором данных, начиная от нескольких параметров командной строки, заканчивая таблицами размером в терабайты.
4393 просмотров
Для того чтобы обеспечить эффективную работу с такими данными далеко не всегда достаточно реализовать алгоритм, который первым пришел в голову. Зачастую необходимо провести тщательную оценку выбранного алгоритма и выбранной структуры данных, так как в большинстве случаев перед разработчиком ставится выбор между быстродействием алгоритма и объемом используемой памяти. Для этих целей используется специальный подход, о котором далее будет идти речь.
Говоря о сложности алгоритма принято иметь ввиду O-нотацию. Данная нотация имеет свои корни в мат. анализе. Говорят, что неотрицательная функция f(n) не превосходит по порядку функцию g(n) и пишут O(f(n)) = O(g(n)) , если существует такая натуральная константа C, что f (n)
Оценка сложности алгоритмов | О большое | Алгоритмы и структуры данных
Для наглядности разберем простой пример. Допустим, нам на вход поступает массив строк. Наша задача заключается в том, чтобы вместо каждой строчки записать в этот массив длину этой строчки. Если наш массив будет состоять из 5 ячеек, то эта операция будет занимать 5 у. е. времени.
Если же их будет 10, то время будет составлять 10 у. е. Рассуждая таким же способом можно прийти к выводу, что время выполнения нашей задачи линейно зависит от числа элементов этого массива, т. е. от размера входных данных. В таком случае, говорится что время выполнения алгоритма не превосходит O(n), где n – число элементов на входе нашего алгоритма.
На практике далеко не всегда можно также легко и однозначно определить зависимость времени выполнения алгоритма от входных данных. Более того, не совсем удобно учитывать каждое малозначимое ответвление. Поэтому для удобной оценки алгоритмов делается несколько допущений, которые значительно упрощают эту задачу.
Первым таким упрощением является то, что мы можем отбросить константы, которые не являются значительными для сравнения. Например, если у нас есть оценка O(n+5), то она эквивалентна O(n). Однако, если нам требуется сравнить O(3n) и O(2n) мы не можем отбросить эти константы и сказать, что алгоритмы эквивалентны с точки зрения времени выполнения.
Следующим упрощением является тот факт, что мы в праве оставлять только самую большую по степени функцию для оценки времени. Например, при оценке O(n^3+n^2 +4n) мы можем упростить ее до оценки O(n^3). Следующее упрощение связно с асимптотикой. Чаще всего, когда нам важно оценить скорость работы алгоритма речь идет о больших объемах информации.
И здесь нам становится не так важно, поступит ли нам на вход миллион или миллион и одна строка. В таких случаях мы говорим о «худшей» или асимптотической оценке алгоритма. То есть в качестве оценки мы принимаем ту функцию, которая является асимптотой для временной составляющей нашего алгоритма.
Когда мы говорим о ситуациях, в которых мы заранее уверены в некоторой структуре входных данных или в объемах этих данных, можно говорить об оценке снизу и средней оценке. Оценка снизу означает, что мы рассчитываем время, которое потребует наш алгоритм в случае наиболее удачной структуры данных и наиболее удачного порядка данных в этой структуре. Если же мы говорим о средней оценке, то нам достаточно просто сложить оценки сверху и снизу и разделить их пополам.
Наиболее распространёнными оценками являются линейная O(n), логарифмическая O(logn), степенная O(m^n) и экспоненциальная O(e^n), так как она удобна для перехода к операциям с логарифмами. Как показывает практика комбинаций этих сложностей достаточно чтобы оценить большинство алгоритмов.
Давайте рассмотрим данный подход на примере оценки алгоритмов сортировки. Ниже приведен код самой простой сортировки «пузырьком»
for i in range(N-1): for j in range(N-i-1): if a[j] > a[j+1]: a[j], a[j+1] = a[j+1], a[j]
Здесь мы видим 2 вложенных цикла. Первый цикл верхнего уровня проходится по элементам от 0 до N-1. Вложенный цикл выполняется N-i-1 раз. Итого оба цикла приблизительно займут N*(N-1)/2 операций. Если вспомнить о том, что мы отбрасываем константы и переменные более низкого порядка получим сложность O(N^2).
Теперь посмотрим на более быстрые алгоритмы сортировки, например, сортировку слиянием. Ниже представлен один из вариантов реализации этого алгоритма.
def merge_sort(nums): if len(nums) > 1: mid = len(nums)//2 left = nums[:mid] right = nums[mid:] merge_sort(left) merge_sort(right) i = j = k = 0 while i < len(left) and j < len(right): if left[i] < right[j]: nums[k] = left[i] i+=1 else: nums[k] = right[j] j+=1 k+=1 while i < len(left): nums[k] = left[i] i+=1 k+=1 while j < len(right): nums[k] = right[j] j+=1 k+=1
В данном алгоритме мы сначала получаем дерево разбиения нашего массива, глубина которого равна log(n). Далее для каждого уровня нашего дерева нам нужно пройтись по n элементам, сравнить их и записать промежуточные результаты. Таким образом сложность данного алгоритма n*log(n). Это в свою очередь быстрее чем рассмотренный ранее алгоритм.
Когда мы оценили несколько алгоритмов с точки зрения времени выполнения, мы можем выбрать алгоритм, который работает быстрее всего. Но в процессе реализации такого алгоритма может возникнуть ситуация, когда для корректной работы необходимо создавать специфические структуры данных, а также дублировать некоторые данные.
В этом случае важно оценить, что для нас является более критичным ресурсом — время или память. Чтобы грамотно это оценить необходимо уметь не только выявлять максимальное и минимальное время работы алгоритма, но и оценивать и оптимизировать структуры, в которые мы записываем данные. Приведем пример.
Если для какого-либо алгоритма нам необходимо дублировать целочисленный массив, этот алгоритм может показаться нам недостаточно эффективным, даже если он дает прирост в скорости в 1.2 раза. Однако, если мы проведем тщательный анализ данных, оценим возможные значения этих самых данных можно прийти к выводу, что вместо int64 здесь вполне применим int32 или даже int16, что нивелирует необходимость дупликации данных и позволяет использовать более быстрый алгоритм.
Но может произойти и более сложная ситуация. Допустим наш алгоритм занимается только операциями поиска вставки и удаления. В голову сразу приходит хэш-таблица, которая позволяет делать все эти операции за константное время.
Однако, если мы знаем, что у нас будет не больше 100 элементов нам стоит еще раз подумать о структуре данных, так как операции получения хэша тоже занимают время, а при использовании новых и сложных алгоритмов хэширования, заточенных на избежание коллизий в больших объемах данных это время может быть несоизмеримо больше того времени, которое мы потенциально экономим при использовании этой структуры. Если вернуться к алгоритмам сортировки, рассмотренным ранее, то можно заметить, что сортировка пузырьком работает с исходными данными и не нуждается в дополнительном выделении памяти, тогда как merge sort требует выделение массива такого же размера, как и исходный. Поэтому в данном случае важно понимать какой длины ожидается массив и хватит ли у нас вычислительных ресурсов для его дублирования.
Таким образом, важно помнить, что за двумя зайцами скорее всего угнаться не получится, поэтому важно четко понимать, что для вас обойдется дороже – память или время. А если удалось и ускорить работу алгоритма и использование памяти сократить, лучше на всякий случай перепроверить расчёты.
Источник: vc.ru
Примеры — Анализ и оценка сложности алгоритмов, О большое, функции.
Это продолжение увлекательной статьи про сложность алгоритмов. . По этой причине всегда необходимо проводить хотя бы поверхностный анализ объемной сложности рекурсивных процедур.
Средний и наихудший случай
Оценка сложности алгоритма до порядка является верхней границей сложности алгоритмов. Если программа имеет большой порядок сложности, это вовсе не означает, что алгоритм будет выполняться действительно долго. На некоторых наборах данных выполнение алгоритма занимает намного меньше времени, чем можно предположить на основе их сложности. Например, рассмотрим код, который ищет заданный элемент в векторе A.
function Locate(data: integer): integer;
var
i: integer;
fl: boolean;
begin
fl:=false; i:=1;
while (not fl) and (i
Если искомый элемент находится в конце списка, то программе придется выполнить N шагов. В таком случае сложность алгоритма составит O(N). В этом наихудшем случае время работы алгоритма будем максимальным.
С другой стороны, искомый элемент может находится в списке на первой позиции. Алгоритму придется сделать всего один шаг. Такой случай называется наилучшим и его сложность можно оценить, как O(1).
Оба эти случая маловероятны. Нас больше всего интересует ожидаемый вариант. Если элемента списка изначально беспорядочно смешаны, то искомый элемент может оказаться в любом месте списка. В среднем потребуется сделать N/2 сравнений, чтобы найти требуемый элемент. Значит сложность этого алгоритма в среднем составляет O(N/2)=O(N).
В данном случае средняя и ожидаемая сложность совпадают, но для многих алгоритмов наихудший случай сильно отличается от ожидаемого. Например, алгоритм быстрой сортировки в наихудшем случае имеет сложность порядка O(N^2), в то время как ожидаемое поведение описывается оценкой O(N*log(N)), что много быстрее.
практическая оценка сложности алгоритмов
Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров.
Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности. Допустим, некоторому алгоритму нужно выполнить 8n 3 + 7n условных операций, чтобы обработать n элементов входных данных. При увеличении n на итоговое время работы будет значительно больше влиять возведение n в куб, чем умножение его на 8 или же прибавление 7n . Тогда говорят, что временная сложность этого алгоритма равна О(n 3 ) , т. е. зависит от размера входных данных кубически. Использование заглавной буквы О (или так называемая О-нотация) пришло из математики, где ее применяют для сравнения асимптотического поведения функций. Формально O(f(n)) означает, что время работы алгоритма (или объем занимаемой памяти) растет в зависимости от объема входных данных не быстрее, чем некоторая константа, умноженная на f(n) .
Примеры
O(n) — линейная сложность
Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придется пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.
O(log n) — логарифмическая сложность
Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нем какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.
O(n 2 ) — квадратичная сложность
Такую сложность имеет, например, алгоритм сортировки вставками. В канонической реализации он представляет из себя два вложенных цикла: один, чтобы проходить по всему массиву, а второй, чтобы находить место очередному элементу в уже отсортированной части. Таким образом, количество операций будет зависеть от размера массива как n * n , т. е. n 2 .
Бывают и другие оценки по сложности, но все они основаны на том же принципе. Также случается, что время работы алгоритма вообще не зависит от размера входных данных. Тогда сложность обозначают как O(1) . Например, для определения значения третьего элемента массива не нужно ни запоминать элементы, ни проходить по ним сколько-то раз.
Всегда нужно просто дождаться в потоке входных данных третий элемент и это будет результатом, на вычисление которого для любого количества данных нужно одно и то же время. Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.
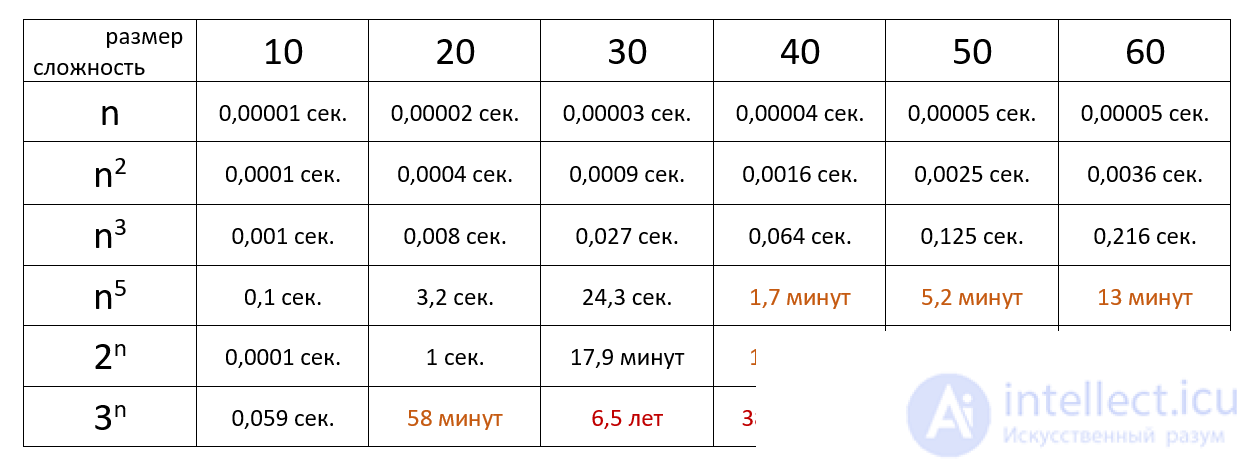
Время выполнения алгоритма с определенной сложностью в зависимости от размера входных данных при скорости 10 6 операций в секунду: Таким образом при запуске алгоритма с разными наборами и обемами данных можно асимтотически построить графики и определить О большое или о маленькое
Общие функции оценки сложности

Сейчас мы перечислим некоторые функции, которые чаще всего используются для вычисления сложности. Функции перечислены в порядке возрастания сложности. Чем выше в этом списке находится функция, тем быстрее будет выполняться алгоритм с такой оценкой.
1. C – константа
2. log(log(N))
3. log(N)
4. N^C, 05. N
6. N*log(N)
7. N^C, C>1
8. C^N, C>1
9. N!
Если мы хотим оценить сложность алгоритма, уравнение сложности которого содержит несколько этих функций, то уравнение можно сократить до функции, расположенной ниже в таблице. Например, O(log(N)+N!)=O(N!).
Если алгоритм вызывается редко и для небольших объемов данных, то приемлемой можно считать сложность O(N^2), если же алгоритм работает в реальном времени, то не всегда достаточно производительности O(N).
Обычно алгоритмы со сложностью N*log(N) работают с хорошей скоростью. Алгоритмы со сложностью N^C можно использовать только при небольших значениях C. Вычислительная сложность алгоритмов, порядок которых определяется функциями C^N и N! очень велика, поэтому такие алгоритмы могут использоваться только для обработки небольшого объема данных.
В заключение приведем таблицу, которая показывает, как долго компьютер, осуществляющий миллион операций в секунду, будет выполнять некоторые медленные алгоритмы.
Эта статья рассказывает о времени выполнения и о расходе памяти большинства алгоритмов используемых в информатике. В прошлом, когда я готовился к прохождению собеседования я потратил много времени исследуя интернет для поиска информации о лучшем, среднем и худшем случае работы алгоритмов поиска и сортировки, чтобы заданный вопрос на собеседовании не поставил меня в тупик. За последние несколько лет я проходил интервью в нескольких стартапах из Силиконовой долины, а также в некоторых крупных компаниях таких как Yahoo, eBay, LinkedIn и Google и каждый раз, когда я готовился к интервью, я подумал: «Почему никто не создал хорошую шпаргалку по асимптотической сложности алгоритмов? ». Чтобы сохранить ваше время я создал такую шпаргалку. Наслаждайтесь!
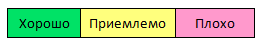
Поиск
Сортировка

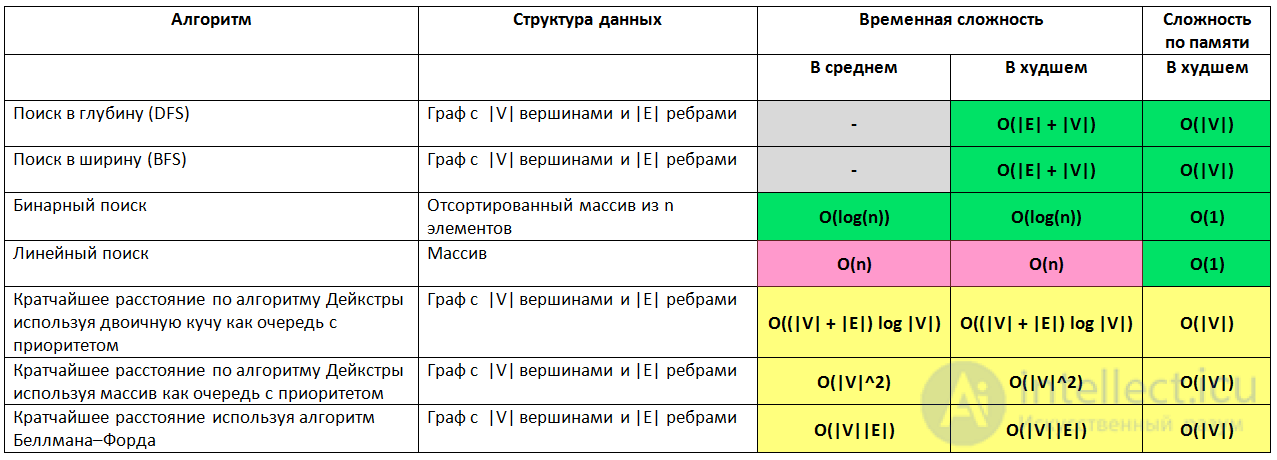
Структуры данных
Кучи
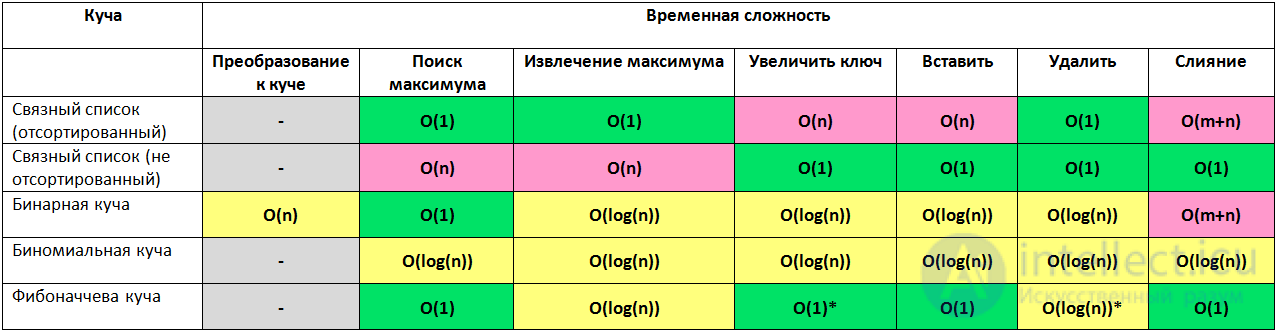
Представление графов
Пусть дан граф с |V| вершинами и |E| ребрами, тогда

Нотация асимптотического роста

- (О — большое) — верхняя граница, в то время как (Омега — большое) — нижняя граница. Тета требует как (О — большое), так и (Омега — большое), поэтому она является точной оценкой (она должна быть ограничена как сверху, так и снизу). К примеру, алгоритм требующий Ω (n logn) требует не менее n logn времени, но верхняя граница не известна. Алгоритм требующий Θ (n logn) предпочтительнее потому, что он требует не менее n logn (Ω (n logn)) и не более чем n logn (O(n logn)).
- f(x)=Θ(g(n)) означает, что f растет так же как и g когда n стремится к бесконечности. Другими словами, скорость роста f(x) асимптотически пропорциональна скорости роста g(n).
- f(x)=O(g(n)). Здесь темпы роста не быстрее, чем g (n). O большое является наиболее полезной, поскольку представляет наихудший случай.
Короче говоря, если алгоритм имеет сложность __ тогда его эффективность __ 
График роста O — большое
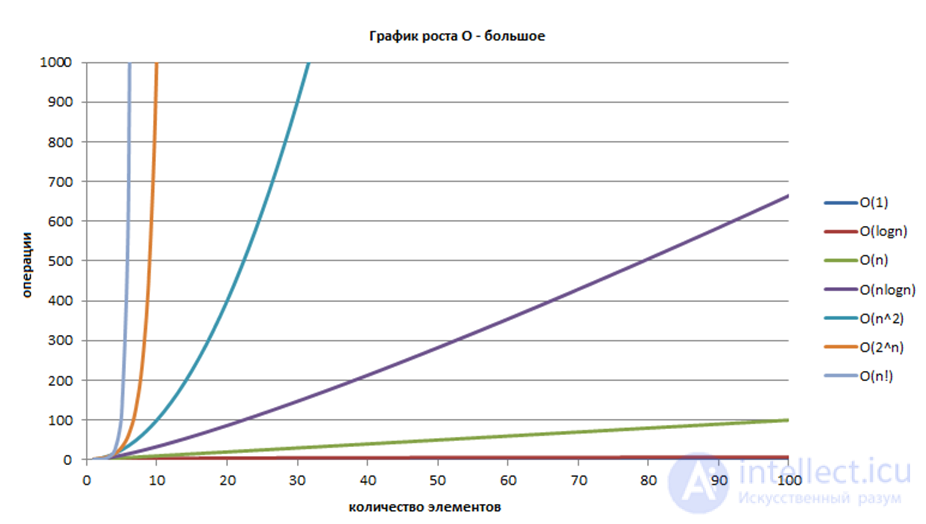
Детальное рассмотрение понятия О большое (Big O)
1. Что такое нотация О большое и почему оно важно
«Нотация О большое — это математическая нотация, которая описывает ограничивающее поведение функции, когда аргумент стремится к определенному значению или бесконечности. Он является членом семейства нотаций, изобретенных Полом Бахманом, Эдмундом Ландау и другими, которые в совокупности называются нотациями Бахмана-Ландау или асимптотическими нотациями ».
Проще говоря, нотация О большое описывает сложность вашего кода с использованием алгебраических терминов.
Чтобы понять, что такое О большое, мы можем взглянуть на типичный пример O (n²), который обычно произносится как «Большой O в квадрате». Буква «n» здесь представляет размер входных данных, а функция «g (n) = n²» внутри «O ()» дает нам представление о том, насколько сложен алгоритм по отношению к количеству входных данных.
Типичным алгоритмом со сложностью O(n²) будет алгоритм сортировки выбором. Сортировка выбором — это алгоритм сортировки, который выполняет итерацию по списку, чтобы гарантировать, что каждый элемент с индексом i является i-м наименьшим/наибольшим элементом списка. Наглядный пример.
Алгоритм может быть описан следующим кодом. Чтобы убедиться, что i-й элемент является i-м наименьшим элементом в списке, этот алгоритм сначала просматривает список с помощью цикла for. Затем для каждого элемента он использует другой цикл for, чтобы найти наименьший элемент в оставшейся части списка.
Источник: intellect.icu