Алгоритм – это описание способа решения задачи, в котором предусматривается разбиения процесса решения на конечную по времени последовательность действий, представленных в виде элементарных операций.
Под элементарной операцией понимается простое действие, которое уже не имеет смысла детализировать.
Алгоритм может использоваться как инструкция для работы, системы управления, автоматического регулятора или другого устройства, выполняющего определённые автоматические действия или операции. Алгоритм может использоваться также в качестве схемы решения определённой задачи.
Алгоритм является основой для составления программы, которую пишет программист на каком-либо языке программирования с тем, чтобы реализовать процесс обработки данных на компьютере.
Алгоритм разбивает весь процесс преобразования информации, связанной с решением определённой задачи, на отдельные, взаимосвязанные между собой этапы. Алгоритм должен точно определять совокупность действий, которые необходимо выполнять на каждом этапе и порядок выполнения этих действий.
Какая программа быстрее? Вычислительная сложность алгоритма.
Решение задач на ЭВМ представляет собой сложный процесс, состоящий из нескольких этапов (рис.1). Разработка алгоритма – это один из этих этапов
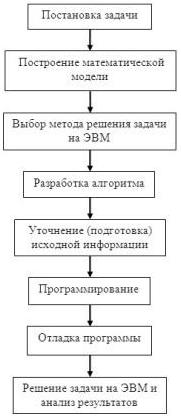
Рисунок 1 — Схема процесса решения задачи на ЭВМ
Постановка задачи – предполагает подробное описание самой задачи, описание входной и выходной информации, формулируется конечная цель, которую необходимо достигнуть при решении задачи. Постановка задачи иногда связана с построением математической модели изучаемого процесса и часто представляет собой довольно сложный этап в решении задачи.
Математическая формулировка – заключается в записи условия задачи помощью математических обозначений, формул, зависимостей, в определении исходных данных и формы выдачи результатов вычислений.
Выбор метода решения задачи на ЭВМ. После построения математической модели необходимо выбрать метод решения задачи на ЭВМ. Выбранный метод является основой построения алгоритма решения задачи.
Разработка алгоритма решения задачи заключается в установлении необходимой последовательности арифметических и логических действий, строгое выполнение которых приводит к решению задачи.
Составление программы – заключается в записи программы на языке программирования.
Отладка программы – этап, необходимый для выявления и устранения ошибок в программе.
Решение задачи на ЭВМ – производится по отлаженной программе для всего множества исходных данных.
Свойства алгоритма
Алгоритм обладает следующими основными свойствами:
- дискретностью;
- определенностью (детерминированностью, точностью);
- массовостью;
- результативностью;
- формальностью.
Дискретность – свойство алгоритма, которое характеризует его структуру. Любой алгоритм состоит из отдельных операций (этапов, действий), которые выполняются дискретно (по шагам). Это означает, что алгоритм обладает свойством дискретности.
Самый подробный урок про Блок-схемы, Понимание, Чтение и Создание блок-схем
Детерминированность – свойство алгоритма, указывающее на то, что каждый шаг алгоритма должен быть строго определен и не может допускать различных толкований. Также строго должен быть определен порядок выполнения отдельных шагов, то есть исполнитель должен точно знать последовательность выполнения операций. Любой алгоритм должен быть представлен таким образом, чтобы он мог быть однозначно (точно) реализован исполнителем. Это свойство алгоритма называют также определенностью, однозначностью или точностью.
Массовость ( универсальность ) – применимость алгоритма ко всем задачам рассматриваемого типа при любых допустимых множествах исходных данных. Здесь важно подчеркнуть, что массовость означает применимость алгоритма ко всем задачам рассматриваемого типа, то есть ко всем задачам, для решения которых он предназначен. Кроме того, здесь необходимо иметь в виду, что реализация алгоритма возможна при любых, но допустимых множествах исходных данных.
Результативность (конечность) — способность получения определенного результата для допустимых исходных данных за конечное число шагов. То есть способность завершать процесс за конечное число итераций или формировать сообщение о невозможности дальнейшей обработки данных (например, в связи с тем, что к имеющимся исходным данным этот алгоритм не применим).
Формальность – свойство означающее, что любой исполнитель, выполняющий алгоритм (например, компьютер), действует формально, то есть строго выполняет инструкции предусмотренные разработчиком алгоритма.
Способы описания алгоритмов
Существуют следующие способы описания (представления) алгоритмов:
- словесное описание;
- описание алгоритма с помощью математических формул;
- графическое описание алгоритма в виде блок-схемы;
- описание алгоритма с помощью псевдокода;
- комбинированный способ изображения алгоритма с использованием словесного, графического и др. способов.
Словесное описание алгоритма представляет собой описание структуры алгоритма на естественном языке. Например, к приборам бытовой техники, как правило, прилагается инструкция по эксплуатации, т.е. словесное описание алгоритма, в соответствии с которым данный прибор должен использоваться.
Графическое описание алгоритма в виде блок-схемы – это описание структуры алгоритма с помощью геометрических фигур с линиями связи.
Блок схема алгоритма – это графическое представление метода решения задачи, в котором используются специальные символы для отображения операций.
Символы, из которых состоит блок-схема алгоритма, определяет ГОСТ 19.701-90. Этот ГОСТ соответствует международному стандарту оформления алгоритмов, поэтому блок-схемы алгоритмов, оформленные согласно ГОСТ 19.701-90, в разных странах понимаются однозначно.
Псевдокод – описание структуры алгоритма на естественном, но частично формализованном языке. В псевдокоде используются некоторые формальные конструкции и общепринятая математическая символика. Строгих синтаксических правил для записи псевдокода не предусмотрено.
Рассмотрим простейший пример. Пусть необходимо описать алгоритм вывода на экран монитора наибольшего значения из двух чисел.
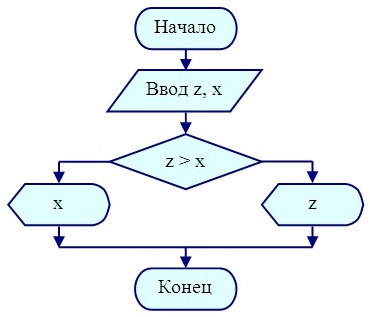
Рисунок 1 — Пример описания алгоритма в виде блок-схемы
Описание этого же алгоритма на псевдокоде:
- Начало
- Ввод чисел: Z, X
- Если Z > X то Вывод Z
- Иначе вывод Х
- Конец
Каждый из перечисленных способов изображения алгоритмов имеет и достоинства и недостатки. Например, словесный способ отличается многословностью и отсутствием наглядности, но дает возможность лучше описать отдельные операции. Графический способ более наглядный, но часто возникает необходимость описать некоторые операции в словесной форме. Поэтому при разработке сложных алгоритмов лучше использовать комбинированный способ.
Структуры алгоритмов
По характеру связей между символами различают алгоритмы линейной, разветвляющейся и циклической структуры.
Линейный алгоритм – это алгоритм, в котором операции выполняются последовательно.
Разветвляющийся алгоритм – это алгоритм, в котором последовательность выполнения операций зависит от определенных условий.
Если в алгоритме присутствует «действие1» и «действие2» (то есть ветвь 1 и ветвь 2), то это разветвляющийся алгоритм с полной альтернативой. Если же вместо «действия2» предусмотрен переход к выполнению операции «n», которая находится в общей (основной) ветви, то такая форма записи называется неполной альтернативой.
Циклический алгоритм – это алгоритм, в котором многократно выполняются одни и те же действия, например с целью многократного выполнения вычислений по одним и тем же зависимостям при различных значениях входящих в них переменных.
Использование циклов существенно сокращает объем алгоритма.
Можно выделить три основных типа циклических алгоритмов:
- цикл с параметром (арифметический цикл или цикл со счетчиком);
- цикл с предусловием;
- цикл с постусловием.
По способу определения числа повторений различают циклы с заранее неизвестным количеством повторений и заранее известным количеством повторений (циклы с параметром).
Цикл с параметром
В цикле с параметром определенная последовательность операций выполняется несколько раз в зависимости от заданной величины, которая называется параметром цикла. Цикл выполняется, пока параметр цикла принимает значения в заданном диапазоне с заданным шагом. Оператор цикла включает имя переменной, конечное значение и шаг.
Цикл с условием
Выделяют два типа циклов с условием: цикл с предусловием и цикл с постусловием.
В циклах с предусловием условие проверяется на входе (до операций, выполняемых в цикле). В циклах с постусловием условие проверяется после выполнения всех операций внутри цикла. В этом случае операторы тела цикла будут реализованы хотя бы один раз или до тех пор, пока не станет возможным условие выхода из цикла.
В ц иклах с постусловием сначала выполняются все операции, включенные в цикл, и только после этого проверяется заданное условие. В зависимости от результата проверки осуществляется выход из цикла или его повторение.
Цикл с условием называют также итерационным циклом.
Внутри алгоритма циклической структуры может быть помещен другой цикл – вложенный цикл, при этом вложенный (внутренний) цикл должен полностью находиться в области внешнего цикла.
Вложенные циклы
Внутри алгоритма циклической структуры может быть помещен другой цикл – вложенный (внутренний) цикл. Вложенный цикл должен полностью находиться в области внешнего цикла. Вложенный цикл может быть один, но может быть и несколько вложенных циклов. Второй вложен в первый, третий – во второй и т.д. Ниже с помощью псевдокода представлена структура циклического алгоритма, содержащего несколько вложенных циклов:
Начало цикла 1
Начало цикла 2
Начало цикла 3
Тело цикла 3
Конец цикла 3
Конец цикла 2
Конец цикла 1
Для организации и внутреннего, и внешнего циклов могут использоваться разные типы алгоритмических структур (цикл с параметром, цикл с предусловием, цикл с постусловием).
На рис. 1 представлена блок-схема алгоритма с внутренним циклом.
В данном случае и внешний и внутренний циклы организованы на базе алгоритмической структуры «цикл с параметром».
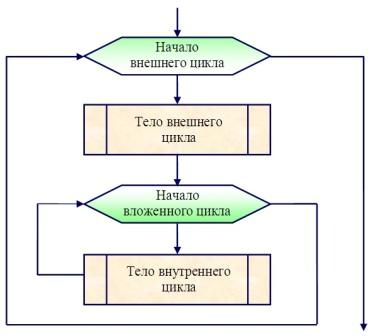
Рисунок 1 – Блок-схема алгоритма с внутренним циклом на базе алгоритмической структуры «цикл с параметром»
На каждом шаге по внешнему циклу внутренний цикл выполняется несколько раз. Количество внутренних циклов на каждом внешнем цикле зависит от параметра внутреннего цикла.
Пусть, например, задано, что параметр внешнего цикла меняется от 1 до 5 с шагом 1, а параметр внутреннего цикла – от 1 до 10 с шагом 1.
Это означает, что на каждом шаге по внешнему циклу внутренний цикл будет выполняться 10 раз. Так как внешний цикл должен выполниться 5 раз, то внутренний цикл выполнится при этом 50 раз.
Источник: poisk-ru.ru
3.4.2.Алгоритмы и способы их описания
Для составления программы, предназначенной для решения на ЭВМ какой-либо задачи, требуется составление алгоритма ее решения.
Алгоритм — это точное предписание, которое определяет процесс, ведущий от получения исходных данных к требуемому конечному результату Алгоритмами, например, являются правила сложения, умножения, решения алгебраических уравнений, умножения матриц и т.п. Слово алгоритм происходит от algoritmi, являющегося латинской транслитерацией арабского имени хорезмийского математика IX века аль-Хорезми. Благодаря латинскому переводу трактата аль-Хорезми европейцы в XII веке познакомились с позиционной системой счисления, и в средневековой Европе алгоритмом называлась десятичная позиционная система счисления и правила счета в ней.
Применительно к ЭВМ алгоритм определяет вычислительный процесс, начинающийся с обработки некоторой совокупности возможных исходных данных и направленный на получение определенных этими исходными данными результатов. Термин вычислительный процесс распространяется и на обработку других видов информации, например, символьной, графической или звуковой.
Если вычислительный процесс заканчивается получением правильных результатов, то говорят, что соответствующий алгоритм применим к рассматриваемой совокупности исходных данных. В противном случае говорят, что алгоритм неприменим к совокупности исходных данных. Любой применимый алгоритм обладает следующими основными свойствами;
- результативностью;
- определенностью;
- массовостью.
Результативность означает возможность получения результата после выполнения конечного количества операций. Определенность состоит в совпадении получаемых результатов независимо от пользователя и применяемых технических. средств. Массовость заключается в возможности применения алгоритма к целому классу однотипных задач, различающихся конкретными значениями исходных данных. Для задания алгоритма необходимо описать следующие его элементы:
- набор объектов, составляющих совокупность возможных исходных данных, промежуточных и конечных результатов;
- правило начала;
- правило непосредственной переработки информации (описание последовательности действий);
- правило окончания;
- правило извлечения результатов.
Алгоритм всегда рассчитан на конкретного исполнителя. В нашем случае таким исполнителем является ЭВМ. Для обеспечения возможности реализации на ЭВМ алгоритм должен быть описан на языке, понятном компьютеру, то есть на языке программирования. Таким образом, можно дать следующее определение программы. Программа для ЭВМпредставляет собой описание алгоритма и данных на некотором языке программирования,предназначенное для последующего автоматического выполнения. Способы описания алгоритмов К основным способам описания алгоритмов можно отнести следующие:
- словесно-формульный;
- структурный или блок-схемный;
- с помощью граф-схем;
- помощью сетей Петри.
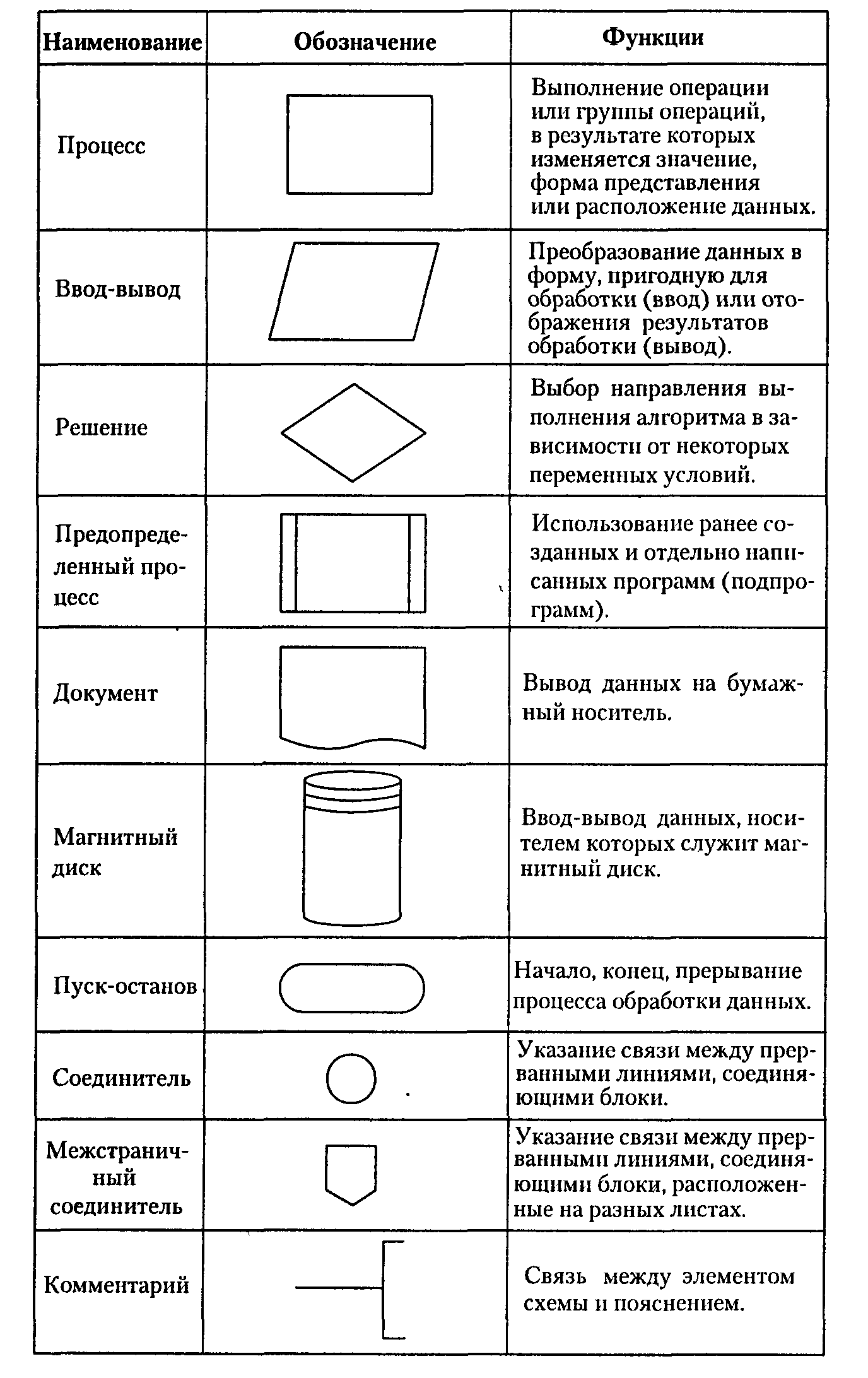
При составлении алгоритмов большинства программ чаще всего используются словесно-формульный и блок-схемный способы. Иногда перед составлением программ на низкоуровневых языках программирования типа языка Ассемблера алгоритм программы записывают, пользуясь конструкциями некоторого высокоуровнего языка программирования. Удобно использовать программное описание алгоритмов функционирования сложных программных систем. Так, для описания принципов функционирования ОС использовался Алголоподобный высокоуровневый язык программирования. При словесно-формульном способе алгоритм записывается в виде текста с формулами по пунктам, определяющим последовательность действий. Пусть, например, необходимо найти значение следующего выражения: у=2а-(х+6). Словесно-формульным способом алгоритм решения этой задачи может быть записан в следующем виде: 1. Ввести значения а и х.2. Сложить х и 6. 3. Умножить а на 2. 4. Вычесть из 2а сумму (х+6). 5. Вывести у как результат вычисления выражения. При блок-схемном описании алгоритм изображается геометрическими фигурами (блоками), связанными по управлению линиями (направлениями потока) со стрелками. В блоках записывается последовательность действий. Первые понятия о блок-схемном описании алгоритмов ввели русские советские математики А.А. Ляпунов и Ю.Н. Янов в 1956 г. Данный способ по сравнению с другими способами записи алгоритма имеет ряд преимуществ. Он наиболее нагляден: каждая операция вычислительного процесса изображается отдельной геометрической фигурой. Кроме того, графическое изображение алгоритма наглядно показывает разветвления путей решения задачи в зависимости от различных условий, повторение отдельных этапов вычислительного процесса и другие детали. Оформление алгоритмов программ должно соответствовать определенным требованиям. Например, в единой системе программной документации (ЕСПД) операции обработки данных и носители информации изображаются на схеме соответствующими блоками. Большая часть блоков по построению условно вписана в прямоугольник со сторонами а и b, размер b= 1,5a. Минимальное значение а равно 10 мм, увеличение а производится на число, кратное 5 мм. В пределах одной схемы рекомендуется изображать блоки одинаковых размеров. Все блоки нумеруются. Виды и назначение основных блоков приведены в табл. 3.1. Линии, соединяющие блоки и указывающие последовательность связей между ними, должны проводится параллельно линиям рамки. Стрелка в конце линии может не ставиться, если линия направлена слева направо или сверху вниз. В блок может входить несколько линий, то есть блок может являться преемником любого числа блоков. Из блока (кроме логического) может выходить только одна линия. Логический блок может иметь в качестве продолжения один из двух блоков, и из него выходят две линии. Если на схеме имеет место слияние линий, то место пересечения выделяется точкой. В случае, когда одна линия подходит к другой и слияние их явно выражено, точку можно не ставить. Схему алгоритмаследует выполнять, как единое целое, однако в случае необходимости допускается обрывать линии, соединяющие блоки. Если при обрыве линии продолжение схемы находится на этом же листе, то на одном и другом конце линии изображается специальный символ соединитель— окружность диаметром 0,5 а. Внутри парных окружностей указывается один и тот же идентификатор. В качестве идентификатора, как правило, используется порядковый номер блока, к которому направлена соединительная линия. Если схема занимает более одного листа, то в случае разрыва линии вместо окружности используется межстраничный соединитель. Внутри каждого соединителя указывается адрес — откуда и куда направлена соединительная линия. Адрес записывается в две строки: в первой указывается номер листа, во второй — порядковый номер блока. Блок-схема должна содержать все разветвления, циклы и обращения к подпрограммам, содержащиеся в программе. Условные обозначения блоков схем алгоритмовТаблица 3.1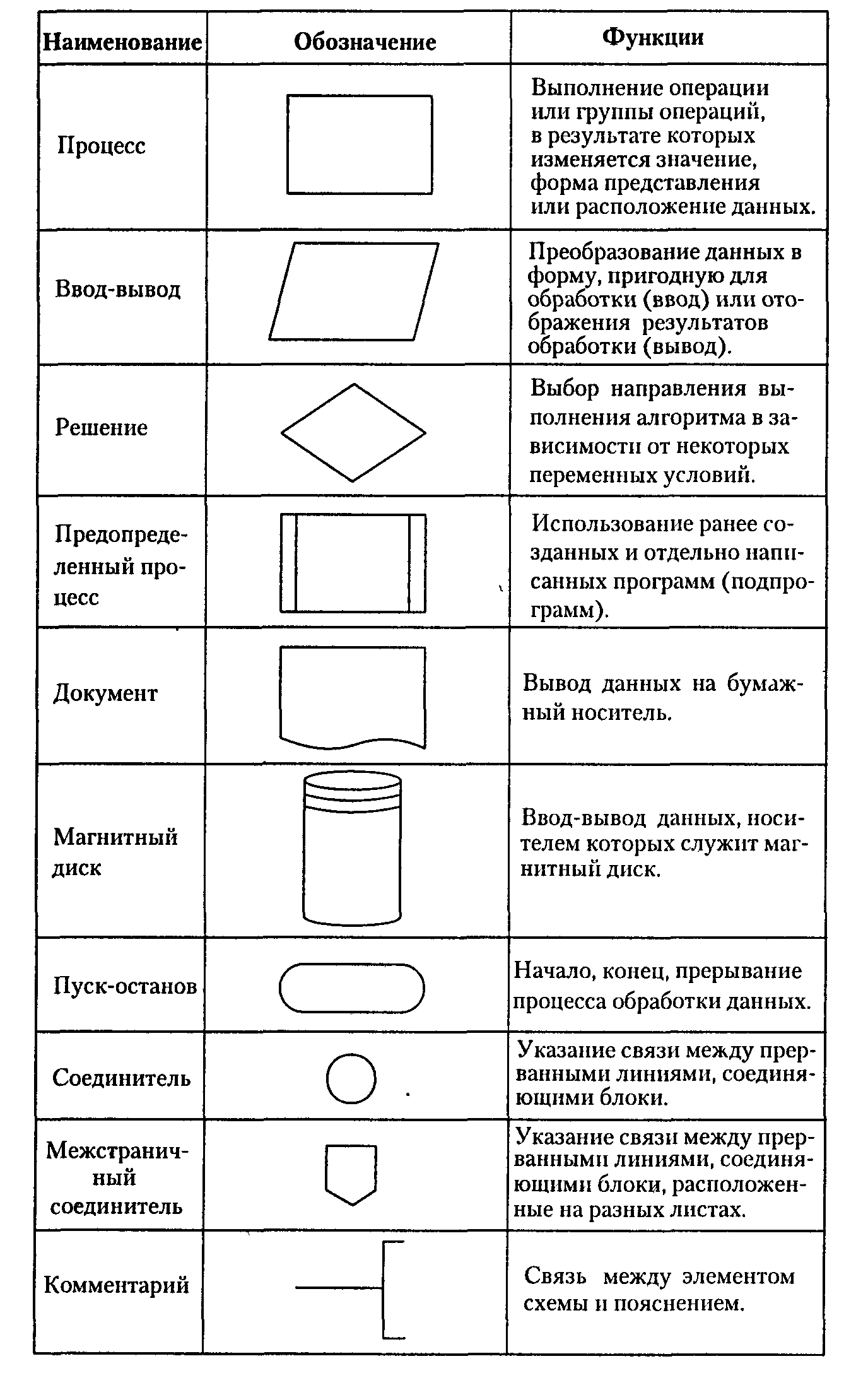
 Структурные схемы алгоритмовОдним из свойств алгоритма являетсядискретность—возможность расчленения процесса вычислений, предписанных алгоритмом, на отдельные этапы, возможность выделения участков программы с определенной структурой. Можно выделить и наглядно представить графически три простейшие структуры:
Структурные схемы алгоритмовОдним из свойств алгоритма являетсядискретность—возможность расчленения процесса вычислений, предписанных алгоритмом, на отдельные этапы, возможность выделения участков программы с определенной структурой. Можно выделить и наглядно представить графически три простейшие структуры:
- последовательность двух или более операций;
- выбор направления;
- повторение.
Любой вычислительный процесс может быть представлен как комбинация этих элементарных алгоритмических структур. Соответственно, вычислительные процессы, выполняемые на ЭВМ по заданной программе, можно разделить на три основных вида:
- линейные;
- ветвящиеся;
- циклические.
Линейным принято называть вычислительный процесс, в котором операции выполняются последовательно, в порядке их записи. Каждая операция является самостоятельной, независимой от каких-либо условий. На схеме блоки, отображающие эти операции, располагаются в линейной последовательности. Линейные вычислительные процессы имеют место, например, при вычислении арифметических выражений, когда имеются конкретные числовые данные и над ними выполняются соответствующие условию задачи действия. На рис. 3.4.2 показан пример линейного алгоритма, определяющего процесс вычисления арифметического выражения у = (b 2 -ac) / (a+c).  Рис. 3.4.2.. Пример линейного алгоритма Вычислительный процесс называется ветвящимся, если для его реализации предусмотрено несколько направлений (ветвей). Каждое отдельное направление процесса обработки данных является отдельной ветвью вычислений. Ветвление в программе — это выбор одной из нескольких последовательностей команд при выполнении программы. Выбор направления зависит от заранее определенного признака, который может относиться к исходным данным, к промежуточным или конечным результатам. Признак характеризует свойство данных и имеет два или более значений. Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей — сложным. Сложный ветвящийся процесс можно представить с помощью простых ветвящихся процессов. Направление ветвления выбирается логической проверкой, в результате которой возможны два ответа: «да» — условие выполнено и «нет» — условие не выполнено. Следует иметь в виду, что, хотя на схеме алгоритма должны быть показаны все возможные направления вычислений в зависимости от выполнения определенного условия (или условий), при однократном прохождении программы процесс реализуется только по одной ветви, а остальные исключаются. Любая ветвь, по которой осуществляются вычисления, должна приводить к завершению вычислительного процесса. На рис. 3.4.3. показан пример алгоритма с разветвлением для вычисления следующего выражения: a + b, если x 0; y = c / b, если x 0.
Рис. 3.4.2.. Пример линейного алгоритма Вычислительный процесс называется ветвящимся, если для его реализации предусмотрено несколько направлений (ветвей). Каждое отдельное направление процесса обработки данных является отдельной ветвью вычислений. Ветвление в программе — это выбор одной из нескольких последовательностей команд при выполнении программы. Выбор направления зависит от заранее определенного признака, который может относиться к исходным данным, к промежуточным или конечным результатам. Признак характеризует свойство данных и имеет два или более значений. Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей — сложным. Сложный ветвящийся процесс можно представить с помощью простых ветвящихся процессов. Направление ветвления выбирается логической проверкой, в результате которой возможны два ответа: «да» — условие выполнено и «нет» — условие не выполнено. Следует иметь в виду, что, хотя на схеме алгоритма должны быть показаны все возможные направления вычислений в зависимости от выполнения определенного условия (или условий), при однократном прохождении программы процесс реализуется только по одной ветви, а остальные исключаются. Любая ветвь, по которой осуществляются вычисления, должна приводить к завершению вычислительного процесса. На рис. 3.4.3. показан пример алгоритма с разветвлением для вычисления следующего выражения: a + b, если x 0; y = c / b, если x 0.  Рис. 3.4.3. Пример разветвляющегося алгоритма Циклическими называются программы, содержащие циклы. Цикл — это многократно повторяемый участок программы. В организации цикла можно выделить следующие этапы:
Рис. 3.4.3. Пример разветвляющегося алгоритма Циклическими называются программы, содержащие циклы. Цикл — это многократно повторяемый участок программы. В организации цикла можно выделить следующие этапы:
- подготовка (инициализация) цикла (И);
- выполнение вычислений цикла (тело цикла) (Т);
- модификация параметров (М);
- проверка условия окончания цикла (У).
Порядок выполнения этих этапов, например, Т и М, может изменяться. В зависимости от расположения проверки условия окончания цикла различают циклы с нижним и верхним окончаниями (рис. 3.4.4). Для цикла с нижним окончанием (рис. 3.4.4. а) тело цикла выполняется как минимум один раз, так как сначала производятся вычисления, а затем проверяется условие выхода из цикла. В случае цикла с верхним окончанием (рис. 3.4.4. б) тело цикла может не выполниться ни разу в случае, если сразу соблюдается условие выхода. Цикл называется детерминированным, если число повторений тела цикла заранее известно или определено. Цикл называется итерационным, если число повторений тела цикла заранее неизвестно, а зависит от значений параметров (некоторых переменных), участвующих в вычислениях. На рис. 3.4.5. показан пример циклического алгоритма вычисления суммы десяти чисел.  Рис. 3.4.4. Примеры циклических алгоритмов
Рис. 3.4.4. Примеры циклических алгоритмов  Рис. 3.4.5. Алгоритм нахождения суммы чисел с 1 до 10 18
Рис. 3.4.5. Алгоритм нахождения суммы чисел с 1 до 10 18
Источник: studfile.net
Алгоритмы
Под элементарной операцией понимается простое действие, которое уже не имеет смысла детализировать.
Алгоритм может использоваться как инструкция для работы, системы управления, автоматического регулятора или другого устройства, выполняющего определённые автоматические действия или операции. Алгоритм может использоваться также в качестве схемы решения определённой задачи.
Алгоритм является основой для составления программы, которую пишет программист на каком-либо языке программирования с тем, чтобы реализовать процесс обработки данных на компьютере.
Алгоритм разбивает весь процесс преобразования информации, связанной с решением определённой задачи, на отдельные, взаимосвязанные между собой этапы. Алгоритм должен точно определять совокупность действий, которые необходимо выполнять на каждом этапе и порядок выполнения этих действий.
Решение задач на ЭВМ представляет собой сложный процесс, состоящий из нескольких этапов (рис.1). Разработка алгоритма – это один из этих этапов

Рисунок 1 — Схема процесса решения задачи на ЭВМ
Постановка задачи – предполагает подробное описание самой задачи, описание входной и выходной информации, формулируется конечная цель, которую необходимо достигнуть при решении задачи. Постановка задачи иногда связана с построением математической модели изучаемого процесса и часто представляет собой довольно сложный этап в решении задачи.
Математическая формулировка – заключается в записи условия задачи помощью математических обозначений, формул, зависимостей, в определении исходных данных и формы выдачи результатов вычислений.
Выбор метода решения задачи на ЭВМ. После построения математической модели необходимо выбрать метод решения задачи на ЭВМ. Выбранный метод является основой построения алгоритма решения задачи.
Разработка алгоритма решения задачи заключается в установлении необходимой последовательности арифметических и логических действий, строгое выполнение которых приводит к решению задачи.
Составление программы – заключается в записи программы на языке программирования.
Отладка программы – этап, необходимый для выявления и устранения ошибок в программе.
Решение задачи на ЭВМ – производится по отлаженной программе для всего множества исходных данных.
Способы описания алгоритмов
Существуют следующие способы описания (представления) алгоритмов:
- словесное описание;
- описание алгоритма с помощью математических формул;
- графическое описание алгоритма в виде блок-схемы;
- описание алгоритма с помощью псевдокода;
- комбинированный способ изображения алгоритма с использованием словесного, графического и др. способов.
Словесное описание алгоритма представляет собой описание структуры алгоритма на естественном языке. Например, к приборам бытовой техники, как правило, прилагается инструкция по эксплуатации, т.е. словесное описание алгоритма, в соответствии с которым данный прибор должен использоваться.
Графическое описание алгоритма в виде блок-схемы – это описание структуры алгоритма с помощью геометрических фигур с линиями связи.
Блок схема алгоритма – это графическое представление метода решения задачи, в котором используются специальные символы для отображения операций.
Символы, из которых состоит блок-схема алгоритма, определяет ГОСТ 19.701-90. Этот ГОСТ соответствует международному стандарту оформления алгоритмов, поэтому блок-схемы алгоритмов, оформленные согласно ГОСТ 19.701-90, в разных странах понимаются однозначно.
Псевдокод – описание структуры алгоритма на естественном, но частично формализованном языке. В псевдокоде используются некоторые формальные конструкции и общепринятая математическая символика. Строгих синтаксических правил для записи псевдокода не предусмотрено.
Рассмотрим простейший пример. Пусть необходимо описать алгоритм вывода на экран монитора наибольшего значения из двух чисел.

Рисунок 1 — Пример описания алгоритма в виде блок-схемы
Описание этого же алгоритма на псевдокоде:
- Начало
- Ввод чисел: Z, X
- Если Z > X то Вывод Z
- Иначе вывод Х
- Конец
Каждый из перечисленных способов изображения алгоритмов имеет и достоинства и недостатки. Например, словесный способ отличается многословностью и отсутствием наглядности, но дает возможность лучше описать отдельные операции. Графический способ более наглядный, но часто возникает необходимость описать некоторые операции в словесной форме. Поэтому при разработке сложных алгоритмов лучше использовать комбинированный способ.
Источник: xn--d1acjinvhdf.xn--p1ai