Рекурсия достаточно распространённое явление, которое встречается не только в областях науки, но и в повседневной жизни. Например, эффект Дросте, треугольник Серпинского и т. д. Самый простой вариант увидеть рекурсию – это навести Web-камеру на экран монитора компьютера, естественно, предварительно её включив. Таким образом, камера будет записывать изображение экрана компьютера, и выводить его же на этот экран, получится что-то вроде замкнутого цикла. В итоге мы будем наблюдать нечто похожее на тоннель.
В программировании рекурсия тесно связана с функциями, точнее именно благодаря функциям в программировании существует такое понятие как рекурсия или рекурсивная функция. Простыми словами, рекурсия – определение части функции (метода) через саму себя, то есть это функция, которая вызывает саму себя, непосредственно (в своём теле) или косвенно (через другую функцию).
Типичными рекурсивными задачами являются задачи: нахождения n!, числа Фибоначчи. Такие задачи мы уже решали, но с использованием циклов, то есть итеративно. Вообще говоря, всё то, что решается итеративно можно решить рекурсивно, то есть с использованием рекурсивной функции. Всё решение сводится к решению основного или, как ещё его называют, базового случая.
Пошаговое объяснение рекурсивной функции Фибоначчи
Существует такое понятие как шаг рекурсии или рекурсивный вызов. В случае, когда рекурсивная функция вызывается для решения сложной задачи (не базового случая) выполняется некоторое количество рекурсивных вызовов или шагов, с целью сведения задачи к более простой. И так до тех пор пока не получим базовое решение. Разработаем программу, в которой объявлена рекурсивная функция, вычисляющая n!
// factorial.cpp: определяет точку входа для консольного приложения. #include «stdafx.h» #include using namespace std; unsigned long int factorial(unsigned long int);// прототип рекурсивной функции int i = 1; // инициализация глобальной переменной для подсчёта кол-ва рекурсивных вызовов unsigned long int result; // глобальная переменная для хранения возвращаемого результата рекурсивной функцией int main(int argc, char* argv[]) < int n; // локальная переменная для передачи введенного числа с клавиатуры cout > n; cout unsigned long int factorial(unsigned long int f) // рекурсивная функция для нахождения n! < if (f == 1 || f == 0) // базовое или частное решение return 1; // все мы знаем, что 1!=1 и 0!=1 cout
// factorial.cpp: определяет точку входа для консольного приложения. #include using namespace std; unsigned long int factorial(unsigned long int);// прототип рекурсивной функции int i = 1; // инициализация глобальной переменной для подсчёта кол-ва рекурсивных вызовов unsigned long int result; // глобальная переменная для хранения возвращаемого результата рекурсивной функцией int main(int argc, char* argv[]) < int n; // локальная переменная для передачи введенного числа с клавиатуры cout > n; cout unsigned long int factorial(unsigned long int f) // рекурсивная функция для нахождения n! < if (f == 1 || f == 0) // базовое или частное решение return 1; // все мы знаем, что 1!=1 и 0!=1 cout
41 Рекурсия в Python. Рекурсивная функция Часть 1
В строках 7, 9, 21 объявлен тип данных unsigned long int , так как значение факториала возрастает очень быстро, например уже 10! = 3 628 800. Если не хватит размера типа данных, то в результате мы получим совсем не правильное значение. В коде объявлено больше операторов, чем нужно, для нахождения n!.
Это сделано для того, чтобы, отработав, программа показала, что происходит на каждом шаге рекурсивных вызовов. Обратите внимание на выделенные строки кода, строки 23, 24, 28 — это рекурсивное решение n!.
Строки 23, 24 являются базовым решением рекурсивной функции, то есть, как только значение в переменной f будет равно 1 или 0 (так как мы знаем, что 1! = 1 и 0! = 1), прекратятся рекурсивные вызовы, и начнут возвращаться значения, для каждого рекурсивного вызова. Когда вернётся значение для первого рекурсивного вызова, программа вернёт значение вычисляемого факториала.
В строке 28 функция factorial() вызывает саму себя, но уже её аргумент на единицу меньше. Аргумент каждый раз уменьшается, чтобы достичь частного решения. Результат работы программы (см. Рисунок 1).
CppStudio.com
Enter n!: 5 Step 1 Result= 0 Step 2 Result= 0 Step 3 Result= 0 Step 4 Result= 0 5!=120
Рисунок 1 — Рекурсия в С++
По результату работы программы хорошо виден каждый шаг и результат на каждом шаге равен нулю, кроме последнего рекурсивного обращения. Необходимо было вычислить пять факториал. Программа сделала четыре рекурсивных обращения, на пятом обращении был найден базовый случай.
И как только программа получила решение базового случая, она порешала предыдущие шаги и вывела общий результат. На рисунке 1 видно всего четыре шага потому, что на пятом шаге было найдено частное решение, что в итоге вернуло конечное решение, т. е. 120. На рисунке 2 показана схема рекурсивного вычисления 5!. В схеме хорошо видно, что первый результат возвращается, когда достигнуто частное решение, но никак не сразу, после каждого рекурсивного вызова.
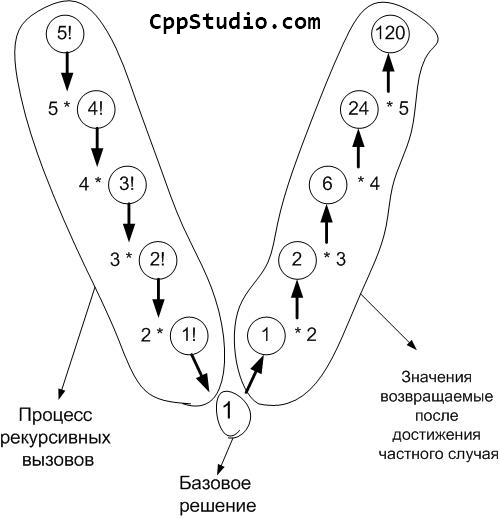
Рисунок 2 — Рекурсия в С++
Итак, чтобы найти 5! нужно знать 4! и умножить его на 5; 4! = 4 * 3! и так далее. Согласно схеме, изображённой на рисунке 2, вычисление сведётся к нахождению частного случая, то есть 1!, после чего по очереди будут возвращаться значения каждому рекурсивному вызову. Последний рекурсивный вызов вернёт значение 5!.
Переделаем программу нахождения факториала так, чтобы получить таблицу факториалов. Для этого объявим цикл for , в котором будем вызывать рекурсивную функцию.
// factorial.cpp: определяет точку входа для консольного приложения. #include «stdafx.h» #include using namespace std; unsigned long int factorial(unsigned long int);// прототип рекурсивной функции int i = 1; // инициализация глобальной переменной для подсчёта кол-ва рекурсивных вызовов unsigned long int result; // глобальная переменная для хранения возвращаемого результата рекурсивной функцией int main(int argc, char* argv[]) < int n; // локальная переменная для передачи введенного числа с клавиатуры cout > n; for (int k = 1; k system(«pause»); return 0; > unsigned long int factorial(unsigned long int f) // рекурсивная функция для нахождения n! < if (f == 1 || f == 0) // базовое или частное решение return 1; // все мы знаем, что 1!=1 и 0!=1 //cout
// factorial.cpp: определяет точку входа для консольного приложения. #include using namespace std; unsigned long int factorial(unsigned long int);// прототип рекурсивной функции int i = 1; // инициализация глобальной переменной для подсчёта кол-ва рекурсивных вызовов unsigned long int result; // глобальная переменная для хранения возвращаемого результата рекурсивной функцией int main(int argc, char* argv[]) < int n; // локальная переменная для передачи введенного числа с клавиатуры cout > n; for (int k = 1; k return 0; > unsigned long int factorial(unsigned long int f) // рекурсивная функция для нахождения n! < if (f == 1 || f == 0) // базовое или частное решение return 1; // все мы знаем, что 1!=1 и 0!=1 //cout
В строках 16 — 19 объявлен цикл, в котором вызывается рекурсивная функция. Всё ненужное в программе закомментированно. Запустив программу, нужно ввести значение, до которого необходимо вычислить факториалы. Результат работы программы показан на рисунке 3.
CppStudio.com
Enter n!: 14 1!=1 2!=2 3!=6 4!=24 5!=120 6!=720 7!=5040 8!=40320 9!=362880 10!=3628800 11!=39916800 12!=479001600 13!=6227020800 14!=87178291200
Рисунок 3 — Рекурсия в С++
Теперь видно, насколько быстро возрастает факториал, кстати говоря, уже результат 14! не правильный, это и есть последствия нехватки размера типа данных. Правильное значение 14! = 87178291200.
Рассмотрим ещё одну типичную задачу — нахождение чисел Фибоначчи, используя рекурсию. Далее приведен код рекурсивного решения такой задачи. Вводим в ком строке порядковый номер числа из ряда Фибоначчи, и программа найдёт все числа из ряда Фибоначчи порядковые номера которых меньше либо равны введённого.
// fibonacci.cpp: определяет точку входа для консольного приложения. #include «stdafx.h» #include // библиотека для форматирования выводимой информации на экран #include using namespace std; unsigned long fibonacci(unsigned long);// прототип рекурсивной функции поиска чисел из ряда Фибоначчи int main(int argc, char* argv[]) < unsigned long entered_number; cout > entered_number; for (int counter = 1; counter unsigned long fibonacci(unsigned long entered_number) // функция принимает один аргумент < if ( entered_number == 1 || entered_number == 2) // частный случай return (entered_number -1); // ряд чисел Фибоначчи всегда начинается с 0, 1, . return fibonacci(entered_number-1) + fibonacci(entered_number-2); // формула поиска н-го числа, например найти восьмое по счёту число, и оно равно 7-е + 6-е >
// fibonacci.cpp: определяет точку входа для консольного приложения. #include // библиотека для форматирования выводимой информации на экран #include using namespace std; unsigned long fibonacci(unsigned long);// прототип рекурсивной функции поиска чисел из ряда Фибоначчи int main(int argc, char* argv[]) < unsigned long entered_number; cout > entered_number; for (int counter = 1; counter unsigned long fibonacci(unsigned long entered_number) // функция принимает один аргумент < if ( entered_number == 1 || entered_number == 2) // частный случай return (entered_number -1); // ряд чисел Фибоначчи всегда начинается с 0, 1, . return fibonacci(entered_number-1) + fibonacci(entered_number-2); // формула поиска н-го числа, например найти восьмое по счёту число, и оно равно 7-е + 6-е >
В строке 6 подключена библиотека для того, чтобы воспользоваться функцией setw() , которая в свою очередь выравнивает первый столбец чисел, то есть номера. Как мы можем заметить, сначала числа однозначные от 1 – 9, а потом идут двузначные. Если убрать данную функцию, то произойдет сдвиг влево чисел от 1 и до 9. Результат работы программы (см. Рисунок 4).
CppStudio.com
Enter number from the Fibonacci series: 30 1 = 0 2 = 1 3 = 1 4 = 2 5 = 3 6 = 5 7 = 8 8 = 13 9 = 21 10 = 34 11 = 55 12 = 89 13 = 144 14 = 233 15 = 377 16 = 610 17 = 987 18 = 1597 19 = 2584 20 = 4181 21 = 6765 22 = 10946 23 = 17711 24 = 28657 25 = 46368 26 = 75025 27 = 121393 28 = 196418 29 = 317811 30 = 514229
Рисунок 4 — Рекурсия в С++
Решение сводится к разбиению сложной задачи к двум более простым. Например, чтобы найти третье число из ряда Фибоначчи, необходимо сначала найти первое и второе, а потом сложить их. Первое число является частным случаем и равно 0 (нулю), второе число также является частным случаем и равно 1. Следовательно, третье число из ряда Фибоначчи равно сумме первого и второго = 1. Приблизительно так же рассуждала запрограммированная нами рекурсивная функция поиска чисел ряда Фибоначчи.
Разработаем ещё одну рекурсивную программу, решающую классическую задачу — «Ханойская башня». Даны три стержня, на одном из которых находится стопка n-го количества дисков, причём диски имеют не одинаковый размер (диски различного диаметра) и расположены таким образом, что по мере прохождения, сверху вниз по стержню диаметр дисков постепенно увеличивается.
То есть диски меньшего размера должны лежать только на дисках большего размера. Необходимо переместить эту стопку дисков с начального стержня на любой другой из двух оставшихся (чаще всего это третий стержень). Один из стержней использовать как вспомогательный. Перемещать можно только по одному диску, при этом диск большего размера никогда не должен находиться над диском меньшего размера.
Допустим необходимо переместить три диска с первого стержня на третий, значит второй стержень вспомогательный. Визуальное решение данной задачи реализовано во Flash. Нажмите на кнопку start , чтобы запустить анимацию, кнопку stop , чтобы остановить.
Программу надо написать для n-го количества дисков. Так как мы решаем данную задачу рекурсивно, то для начала необходимо найти частные случаи решения. В данной задаче частный случай только один – это когда необходимо переместить всего один диск, и в этом случае даже вспомогательный стержень не нужен, но на это просто не обращаем внимания. Теперь необходимо организовать рекурсивное решение, в случае, если количество дисков больше одного. Введём некоторые обозначения, для того, чтоб не писать лишнего:
— стержень, на котором изначально находятся диски (базовый стержень);
— вспомогательный или промежуточный стержень;
— финальный стержень – стержень, на который необходимо переместить диски.
Далее, при описании алгоритма решения задачи будем использовать эти обозначения. Чтобы переместить три диска с на нам необходимо сначала переместить два диска с на а потом переместить третий диск(самый большой) на , так как свободен.
Для того, чтобы переместить n дисков с на нам необходимо сначала переместить n-1 дисков с на а потом переместить n-й диск(самый большой) на , так как свободен. После этого необходимо переместить n-1 дисков с на , при этом использовать стержень как вспомогательный. Эти три действия и есть весь рекурсивный алгоритм. Этот же алгоритм на псевдокоде:
n-1 переместить на
n переместить на
n-1 переместить с на , при этом использовать как вспомогательный
// hanoi_tower.cpp: определяет точку входа для консольного приложения. // Программа, рекурсивно решающая задачу «Ханойская башня» #include «stdafx.h» #include #include using namespace std; void tower(int, int, int, int); // объявление прототипа рекурсивной функции int count = 1; // глобальная переменная для подсчёта количества шагов int _tmain(int argc, _TCHAR* argv[]) < cout > number; cout > basic_rod; cout > final_rod; int help_rod; // блок определения номера вспомогательного стержня, анализируя номера начального и финального стержня if (basic_rod != 2 final_rod != 2 ) help_rod = 2; else if (basic_rod != 1 final_rod != 1 ) help_rod = 1; else if (basic_rod != 3 final_rod != 3 ) help_rod = 3; tower(// запуск рекурсивной функции решения задачи Ханойских башен number, // переменная, хранящая количество дисков, которые надо переместить basic_rod, // переменная, хранящая номер стержня, на котором диски будут находится изначально help_rod , // переменная, хранящая номер стержня, который используется, как вспомогательный final_rod); // переменная, хранящая номер стержня, на который необходимо переместить диски system(«pause»); return 0; > void tower(int count_disk, int baza, int help_baza, int new_baza) < if ( count_disk == 1) // условие завершения рекурсивных вызовов < cout » else < tower(count_disk -1, baza, new_baza, help_baza); // перемещаем все диски кроме самого последнего на вспомогательный стержень tower(1, baza, help_baza, new_baza); // перемещаем последний диск с начального стержня на финальный стержень tower(count_disk -1, help_baza, baza, new_baza); // перемещаем все диски со вспомогательного стержня на финальный >>
// hanoi_tower.cpp: определяет точку входа для консольного приложения. // Программа, рекурсивно решающая задачу «Ханойская башня» #include #include using namespace std; void tower(int, int, int, int); // объявление прототипа рекурсивной функции int count = 1; // глобальная переменная для подсчёта количества шагов int main() < cout > number; cout > basic_rod; cout > final_rod; int help_rod; // блок определения номера вспомогательного стержня, анализируя номера начального и финального стержня if (basic_rod != 2 final_rod != 2 ) help_rod = 2; else if (basic_rod != 1 final_rod != 1 ) help_rod = 1; else if (basic_rod != 3 final_rod != 3 ) help_rod = 3; tower(// запуск рекурсивной функции решения задачи Ханойских башен number, // переменная, хранящая количество дисков, которые надо переместить basic_rod, // переменная, хранящая номер стержня, на котором диски будут находится изначально help_rod , // переменная, хранящая номер стержня, который используется, как вспомогательный final_rod); // переменная, хранящая номер стержня, на который необходимо переместить диски return 0; > void tower(int count_disk, int baza, int help_baza, int new_baza) < if ( count_disk == 1) // условие завершения рекурсивных вызовов < cout » else < tower(count_disk -1, baza, new_baza, help_baza); // перемещаем все диски кроме самого последнего на вспомогательный стержень tower(1, baza, help_baza, new_baza); // перемещаем последний диск с начального стержня на финальный стержень tower(count_disk -1, help_baza, baza, new_baza); // перемещаем все диски со вспомогательного стержня на финальный >>
На рисунке 5 показан пример работы рекурсивной программы Ханойская башня. Сначала мы ввели количество дисков равное трём, потом ввели базовый стержень (первый), и обозначили конечный стержень (третий). Автоматически второй стержень стал вспомогательным. Программа выдала такой результат, что он полностью совпадает с анимационным решением данной задачи.
CppStudio.com
Enter of numbers of disks: 3 Enter the number of basic rod: 1 Enter the number of final rod: 3 1) 1 -> 3 2) 1 -> 2 3) 3 -> 2 4) 1 -> 3 5) 2 -> 1 6) 2 -> 3 7) 1 -> 3
Рисунок 5 — Рекурсия в С++
Из рисунка видно, что сначала перемещается диск со стержня один на стержень три, потом со стержня один на стержень два, со стержня три на стержень два и т. д. То есть программа всего лишь выдает последовательность перемещений дисков и минимальное количество шагов, за которые будут перемещены все диски.
Все эти задачи можно было решить итеративно. Возникает вопрос: “Как лучше решать, итеративно или рекурсивно?”. Отвечаю: “Недостаток рекурсии в том, что она затрачивает значительно больше компьютерных ресурсов, нежели итерация. Это выражается в большой нагрузке, как на оперативную память, так и на процессор.
Если очевидно решение той или иной задачи итеративным способом, то им и надо воспользоваться иначе, использовать рекурсию!” В зависимости от решаемой задачи сложность написания программ изменяется при использовании того или иного метода решения. Но чаще задача, решённая рекурсивным методом с точки зрения читабельности кода, куда понятнее и короче.
Источник: cppstudio.com
Как написать рекурсивную программу
Рекурсивные функции — это функции, которые вызывают сами себя. Такие функции довольно часто используются для обхода различных представлений. Например, если нам надо найти определенный файл в папке, то мы сначала смотрим все файлы в этой папке, затем смотрим все ее подпак
Например, определим вычисление факториала в виде рекурсивной функции:
#include unsigned long long factorial(unsigned); int main() < unsigned n ; auto result < factorial(n)>; std::cout unsigned long long factorial(unsigned n) < if(n >1) return n * factorial(n-1); return 1; >
В функции factorial задано условие, что если число n больше 1, то это число умножается на результат этой же функции, в которую в качестве параметра передается число n-1. То есть происходит рекурсивный спуск. И так далее, пока не дойдем того момента, когда значение параметра не будет равно 1. В этом случае функция возвратит 1.
Рекурсивная функция обязательно должна иметь некоторый базовый вариант, который использует оператор return и к которому сходится выполнение остальных вызовов этой функции. В случае с факториалом базовый вариант представлен ситуацией, при которой n = 1. В этом случае сработает инструкция return 1; .
Например, при вызове factorial(5) получится следующая цепь вызовов:
- 5 * factorial(4)
- 5 * 4 * factorial(3)
- 5 * 4 * 3 * factorial(2)
- 5 * 4 * 3 * 2 * factorial(1)
- 5 * 4 * 3 * 2 * 1
Другим распространенным показательным примером рекурсивной функции служит функция, вычисляющая числа Фиббоначчи. n-й член последовательности чисел Фибоначчи определяется по формуле: f(n)=f(n-1) + f(n-2), причем f(0)=0, а f(1)=1. Значения f(0)=0 и f(1)=1, таким образом, определяют базовые варианты для данной функции:
#include unsigned long long fib(unsigned); int main() < for(unsigned i<>; i < 10; i++) < auto n = fib(i); std::cout std::cout unsigned long long fib(unsigned n)
Результат работы программы — вывод 10 чисел из последовательности Фиббоначчи на консоль:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34
В примерах выше функция напрямую вызывала саму себя. Но рекурсивный вызов функции также может быть косвенным. Например, функция fun1() вызывает другую функцию fun2(), которая, в свою очередь, вызывает fun1(). В этом случае функции fun1() и fun2() также называются взаимно рекурсивными функциями.
Стоит отметить, что нередко рекурсивные функции можно представить в виде циклов. Например, для вычисления факториала вместо рекурсии используем цикл:
#include unsigned long long factorial(unsigned); int main() < unsigned n ; std::cout unsigned long long factorial(unsigned n) < unsigned long long result; for(unsigned i; i return result; >
И нередко циклические конструкции более эффективны, чем рексурсия. Например, если функция вызывает себя тысячи раз, потребуется большой объем стековой памяти для хранения копий значений аргументов и адреса возврата для каждого вызова, что может привести к тому, что программа быстро исчерпает выделенную для нее память стека, поскольку объем памяти стека обычно фиксирован и ограничен. что может привести к аварийному завершению программы. Поэтому в таких случаях, как правило, лучше использовать альтернативные подходы, например цикл. Однако, несмотря на накладные расходы, использование рекурсии часто может значительно упростить написание программы.
Источник: metanit.com
Рекурсивные функции
Любая функция в программе на языке C может вызываться рекурсивно, т. е. может вызывать сама себя. Число рекурсивных вызовов ограничено размером стека. Сведения о параметрах компоновщика, определяющих размер стека, см. в описании параметра компоновщика /STACK (распределения стека).
При каждом вызове функции для параметров и переменных auto и register выделяется новая память, чтобы не перезаписывались их значения в предыдущих (незаконченных) вызовах. Параметры доступны непосредственно только экземпляру функции, в котором они были созданы. Последующим экземплярам функции предыдущие параметры непосредственно недоступны.
Обратите внимание, что для переменных, объявленных с описателем static , новая память при новом рекурсивном вызове не требуется. Их память существует в течение времени жизни программы. При каждой ссылке на такую переменную осуществляется доступ к той же области памяти.
Пример
В следующем примере демонстрируются рекурсивные вызовы.
int factorial( int num ); /* Function prototype */ int main() < int result, number; . . . result = factorial( number ); >int factorial( int num ) /* Function definition */ < . . . if ( ( num >0 ) || ( num
Источник: learn.microsoft.com