Калькулятор у нас почему-то ассоциируется с чем-то, что должен написать каждый новичок. Возможно потому, что исторически компьютеры с той целью и создавались, чтобы считать. Но мы будем писать непростой калькулятор, не sympy конечно, но чтобы умел базовые алгебраические операции, типа дифференциирования, симплификации, а также фичи типа компиляции для ускорения вычислений.
Меньше воды! О чем статья?
Здесь будет поверхностно о построении выражения, парсинге из строки, подстановки переменной, аналитической производной, численным решении уравнения и определенного интеграла, рендеринг в формат LaTeX, комплексных числах, компиляцией функций, упрощении, раскрытии скобок, и бла бла бла. Вероятно, не в одной статье.
Для тех, кому нужно срочно что-нибудь склонировать, ссылка на репозиторий.
Берем оставшиеся с нового года печеньки, и погнали!
Для кого эта статья?
Я думаю, что статья может быть полезна новичку, но может быть те, кто чуть поопытнее, тоже найдут что-то интересное. Впрочем, я надеюсь написать статью так, чтобы ее можно было читать и не будучи C# программистом вообще.
Python с нуля. Пишем программу для вычисления идеального веса
Сборка выражения
Что такое «выражение»?
Когда я был маленький.
То я конечно хотел написать калькулятор. Что он должен уметь делать? Четыре основные операции, и в принципе куда еще больше. Так, моей задачей было посчитать значение строкового выражения, например «1 + (3 / 4 — (5 + 3 * 1))». Я взял мою любимую дельфи, и написал парсер, который сначала рекурсивно уходил в скобочки, а потом выражение в скобках заменял на значение, а скобки убирал.
В принципе, вполне рабочий способ для меня в то время.
Конечно, это не строка. Довольно очевидно, что математическая формула — это либо дерево, либо стек, и здесь мы остановимся на первом. То есть каждая нода, каждый узел этого дерева, это какая-то операция, переменная, либо константа.
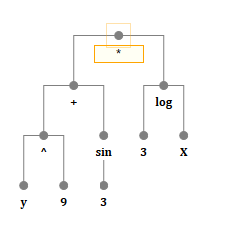
Операция — это либо функция, либо оператор, в принципе, примерно одно и то же. Ее дети — аргументы функции (оператора).
Иерархия классов в вашем коде
Разумеется, реализация может быть любой. Однако идея в том, что если ваше дерево состоит только из узлов и листьев, то они бывают разными. Поэтому я называю эти «штуки» — сущностями. Поэтому верхним классом у нас будет абстрактный класс Entity.
Абстрактный?
Как все знают из базового изучения языка, абстрактный класс хорош тем, что с одной стороны обобщает какие-то классы, с другой стороны позволяет разделить логику и поведение некоторых объектов. Объект абстрактного класса нельзя создать, а вот его наследника — можно.
А также будет четыре класса-наследника: NumberEntity, VariableEntity, OperatorEntity, FunctionEntity.
Как построить выражение?
Для начала мы будем строить выражение в коде, то есть
var x = new VariableEntity(«x»); var expr = x * x + 3 * x + 12;
Если объявить пустой класс VariableEntity, то такой код выкинет вам ошибку, мол не знает как умножать и суммировать.
Как сделать калькулятор на Python? | Делаем свой калькулятор
Переопределение операторов
Очень важная и полезная фича большинства языков, позволяя кастомизировать выполнение арифметических операций. Синтаксически реализуется по-разному в зависимости от языка. Например, реализация в C#
public static YourClass operator +(YourClass a, YourClass b)
(Не)явное приведение типов
В компилируемых языках типа C# такая штука обычно присутствует и позволяет без дополнительного вызова myvar.ToAnotherType() привести тип, если необходимо. Так, например, было бы удобно писать
NumberEntity myvar = 3;
NumberEntity myvar = new NumberEntity(3);
Подвешивание
Класс Entity имеет поле Children — это просто список Entity, которые являются аргументами для данной сущности.
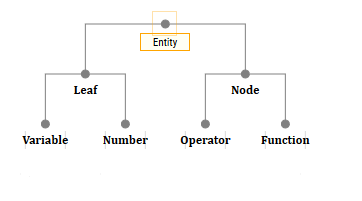
Вообще-то детей могут иметь объекты лишь двух классов: OperatorEntity и FunctionEntity. То есть в принципе можно было бы создать какой-нибудь NodeEntity и у него унаследовать эти два класса, и создать LeafEntity и от него унаследовать VariableEntity и NumberEntity.
Когда у нас вызывается функция или оператор, нам стоит создать новую сущность, и в ее дети положить то, от чего вызывается функция или оператор. К примеру, сумма по идее должна выглядить примерно так:
public static Entity operator +(Entity a, Entity b)
То есть теперь если у нас есть сущность x и сущность 3, то x+3 вернет сущность оператора суммы с двумя детьми: 3 и x. Так, мы можем строить деревья выражений.
Вызов функции более простой и не такой красивый, как с оператором:
public Entity Sin(Entity a)
Подвешивание в репе реализовано тут.
Отлично, мы составили дерево выражений.
Подстановка переменной
Здесь все предельно просто. У нас есть Entity — мы проверяем является ли он сам переменной, если да, возвращаем значение, иначе — бежим по детям.
В этом огромном 48-строчном файле реализована столь сложная функция.
Вычисление значения
Собственно то, ради чего все это. Здесь мы по идее должны добавить в Entity какой-то такой метод
public Entity Eval() < if (IsLeaf) < return this; >else return MathFunctions.InvokeEval(Name, Children); >
Листик без изменений, а для всего остального у нас кастомное вычисление. Опять же, приведу лишь пример:
public static Entity Eval(List args)
Если аргумент — число, то произведем численную функцию, иначе — вернем как было.
Number?
Это самая простая единица, число. Над ним можно проводить арифметические операции. По умолчанию оно комплексное. Также у него определены такие операции как Sin, Cos, и некоторые другие.
Если интересно, Number описан тут.
Производная
Численно производную посчитать может кто угодно, и такая функция пишется поистине в одну строку:
public double Derivative(Func f, double x) => (f(x + 1.0e-5) — f(x)) * 1.0e+5;
Но разумеется нам хочется аналитическую производную. Так как у нас уже есть дерево выражений, мы можем рекурсивно заменить каждый узел в соответствии с правилом дифференциирования. Работать оно должно примерно так:

Вот, к примеру, как реализованна сумма в моем коде:
public static Entity Derive(List args, VariableEntity variable)
А вот произведение
public static Entity Derive(List args, VariableEntity variable)
А вот сам по себе обход:
public Entity Derive(VariableEntity x) < if (IsLeaf) < if (this is VariableEntity this.Name == x.Name) return new NumberEntity(1); else return new NumberEntity(0); >else return MathFunctions.InvokeDerive(Name, Children, x); >
Это метод Entity. И как видим, что у листа всего два состояния — либо это переменная, по которой мы дифференциируем, тогда ее производная равна 1, либо это константа (число либо VariableEntity), тогда ее производная 0, либо узел, тогда идет отсылка по имени (InvokeDerive обращается к словарю функций, где и находится нужная (например сумма или синус)).
Заметьте, я здесь не оставляю что-то типа dy/dx и сразу говорю, что производная от переменной не по которой мы дифференциируем равна 0. А вот здесь сделано по-другому.
Все дифференциирование описано в одном файле, а больше и не надо.
Упрощение выражения. Паттерны
Упрощение выражения в общем случае в принципе нетривиально. Ну например, какое выражение проще: или ? Но мы придерживаемся каких-то представлений, и на основе них хотим сделать те правила, которые точно упрощают выражение.
Можно при каждом Eval писать, что если у нас сумма, а дети — произведения, то переберем четыре варианта, и если где-то что-то равно, вынесем множитель… Но так делать конечно же не хочется. Поэтому можно догадаться до системы правил и паттернов. Итак, что мы хотим? Примерно такой синтаксис:
< any1 / (any2 / any3) ->any1 * any3 / any2 >, < const1 * var1 + const2 * var1 ->(const1 + const2) * var1 >, < any1 + any1 * any2 ->any1 * (Num(1) + any2) >,
Вот пример дерева, в котором нашлось поддерево (обведено в зеленый), отвечающее паттерну any1 + const1 * any1 (найденное any1 обведено в оранжевый).

Как видим, иногда нам важно, что одна и та же сущность должна повторяться, например чтобы сократить выражение x + a * x нам необходимо, чтобы и там и там был x, ведь x + a * y уже не сокращается. Поэтому нам нужно сделать алгоритм, который не только проверяет, что дерево соответсвует паттерну, но и
- Проверять, что одинаковые паттерновые Entity соответствуют одинаковым Entity.
- Записывать, что чему соответствует, чтобы потом подставить.
internal Dictionary EqFits(Entity tree) < var res = new Dictionary(); if (!tree.PatternMakeMatch(this, res)) return null; else return res; >
А в tree.PaternMakeMatch мы рекурсивно наполняем словарь ключами и их значениями. Вот пример списка самих паттерных Entity:
static readonly Pattern any1 = new Pattern(100, PatType.COMMON); static readonly Pattern any2 = new Pattern(101, PatType.COMMON); static readonly Pattern const1 = new Pattern(200, PatType.NUMBER); static readonly Pattern const2 = new Pattern(201, PatType.NUMBER); static readonly Pattern func1 = new Pattern(400, PatType.FUNCTION);
Когда мы будем писать any1 * const1 — func1 и так далее, у каждой ноды будет номер — это и есть ключ. Иначе говоря, при заполнении словаря, ключами выступят как раз эти номера: 100, 101, 200, 201, 400… А при постройке дерева мы будем смотреть на значение, соответствующее ключу, и подставлять его.
Упрощение. Сортировка дерева
В статье, к которой я уже обращался, автор решил сделать просто, и отсортировал практически по хешу дерева. Ему удалось сократить a и -a, b + c + b превратить 2b + c. Но мы, конечно, хотим и чтобы (x + y) + x * y — 3 * x сокращалось, и в целом более сложные штуки.
Паттерны не работают?
Вообще, то, что мы сделали до этого, паттерны — чудовищно замечательная штука. Она позволит вам сокращать и разность квадратов, и сумму квадрата синуса и косинуса, и другие сложные штуки. Но элементарную пальму, ((((x + 1) + 1) + 1) + 1), она не сократит, ведь здесь главное правило — коммутативность слагаемых. Поэтому первый шаг — вычленить «линейных детей».
«Линейные дети»
Собственно для каждой ноды суммы или разности (и, кстати, произведения/деления) мы хотим получить список слагаемых (множителей).
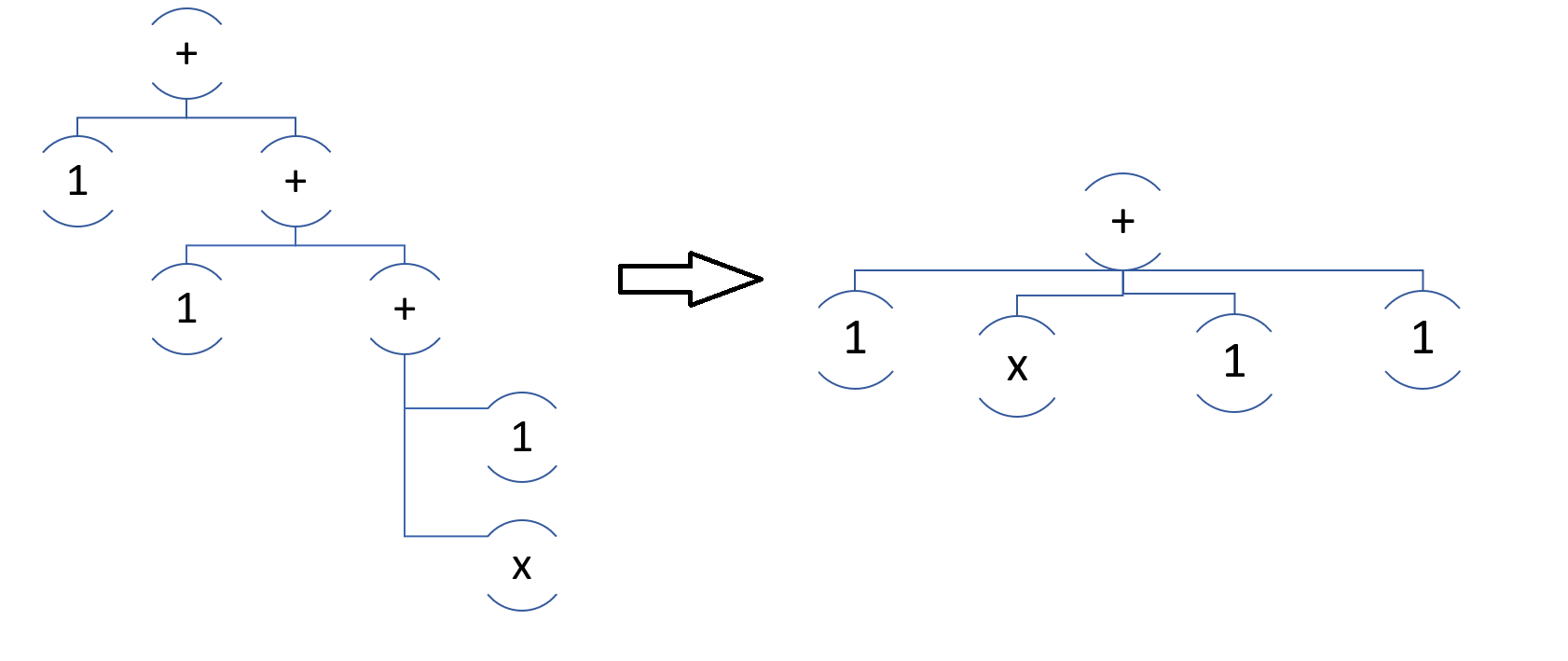
Это в принципе несложно. Пусть функция LinearChildren(Entity node) возвращает список, тогда мы смотрим на child in node.Children: если child — это не сумма, то result.Add(child), иначе — result.AddRange(LinearChildren(child)).
Не самым красивым образом реализовано тут.
Группировка детей
Итак, у нас есть список детей, но что дальше? Допустим, у нас есть sin(x) + x + y + sin(x) + 2 * x. Очевидно, что наш алгоритм получит пять слагаемых. Далее мы хотим сгруппировать по похожести, например, x похож на 2 * x больше, чем на sin(x).
Вот хорошая группировка:
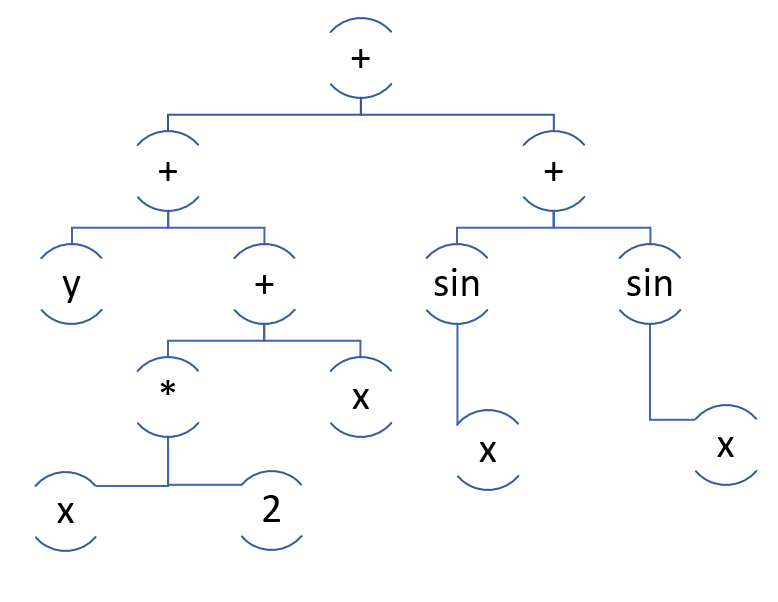
Так как в ней паттерны дальше справятся с преобразованием 2*x + x в 3*x.
То есть мы сначала группируем по некоторому хешу, а затем делаем MultiHang — преобразование n-арного суммирования в бираное.
Хеш узла
С одной стороны, и следует поместить в одну группу. С другой стороны, при наличии помещать в одну группу с бессмысленно.
Если подумать, то . Хотя мне кажется, это практически не проще, и уж точно не нужно. Да и вообще, упрощение — вещь ни разу неочевидная, и уж это точно не первое, что стоит писать при написании «калькулятора».
Поэтому мы реализовываем многоуровневую сортировку. Сначала мы делаем вид, что — одно и то же. Посортировали, успокоились. Потом делаем вид, что можно помещать только с другими . И вот уже наши и наконец объединились. Реализовано достаточно просто:
internal string Hash(SortLevel level)
Как видим, функция по-любому влияет на сортировку (разумеется, ведь с вообще никак в общем случае не связана). Как и переменная, с ну никак не получится смешать. А вот константы и операторы учитываются не на всех уровнях. В таком порядке идет сам процесс упрощения
public Entity Simplify(int level) < // Сначала мы делаем самую простую симплификацю: вычисление значений там, где это возможно, умножение на ноль и т. д. var stage1 = this.InnerSimplify(); Entity res = stage1; for (int i = 0; i < level; i++) < // Этот блок ответственнен за сортировку. Сначала мы группируем что-то типа x и x+1 (переменные и функции), затем что-то типа x-1 и x+1 (переменные, функции и константы), затем что-то типа x+1 и x+1 (учитывается все). switch (i) < case 0: res = res.Sort(SortLevel.HIGH_LEVEL); break; case 2: res = res.Sort(SortLevel.MIDDLE_LEVEL); break; case 4: res = res.Sort(SortLevel.LOW_LEVEL); break; >// Здесь мы заменяем паттерны. res = TreeAnalyzer.Replace(Patterns.CommonRules, res).InnerSimplify(); > return res; >
Самая ли это лучшая реализация? Пихните в личные сообщения, может быть будут идеи получше. Я долго думал, как сделать это макимально красиво, хотя по моему мнению, до «красиво» здесь далеко.
«Компиляция» функций
В кавычках — так как не в сам IL код, а лишь в очень быстрый набор инструкций. Но зато очень просто.
Проблема Substitute
Чтобы посчитать значение функции, нам достаточно вызвать подстановку переменной и eval, например
var x = MathS.Var(«x»); var expr = x * x + 3; var result = expr.Substitute(x, 5).Eval();
Но это работает медленно, около 1.5 микросекунды на синус.
Инструкции
Чтобы ускорить вычисление, мы делаем вычисление функции на стеке, а именно:
1) Придумываем класс FastExpression, у которого будет список инструкций
2) При компиляции инструкции складываются в стек в обратном порядке, то есть если есть функция x * x + sin(x) + 3, то инструкции будут примерно такими:
PUSHVAR 0 // Подстановка переменной номер 0 — x CALL 6 // Вызов функции номер 6 — синуса PUSHCONST 3 CALL 0 // Вызов функции номер 0 — суммы PUSHVAR 0 PUSHVAR 0 CALL 2 CALL 0
Далее при вызове мы прогоняем эти инструкции и возвращаем Number.
Пример выполнения инструкции суммы:
internal static void Sumf(Stack stack)
Вызов синуса сократился с 1500нс до 60нс (системный Complex.Sin работает за 30нс).
В репе реализовано тут.
Фух, вроде бы пока все. Хотя рассказать еще есть о чем, но мне кажется объем для одной статьи достаточный. Интересно ли кому-нибудь продолжение? А именно: парсинг из строки, форматирование в латех, определенный интеграл, и прочие плюшки.
Ссылка на репозиторий со всем кодом, а также тестами и самплами.
Вообще-то я продолжаю работать над этим проектом. Распространяется он под MIT (то есть делайте с ним что хотите), и он никогда не станет ни закрытым, ни коммерческим. Более того, если есть идеи для улучшения и вклада — pull-реквесты очень приветствуются.
Источник: habr.com
Простой калькулятор на JavaScript
Сегодня сделаем простейший калькулятор на JavaScript, но не просто так, а с умыслом. Позднее мы представим, что мы тестировщики, и попробуем протестировать этот калькулятор. Вернее, не протестировать, а дико сломать.
Что делаем
На старте у нас будет самый простой калькулятор, который сможет только складывать, вычитать, умножать и делить два числа. Этого уже будет достаточно, чтобы потренироваться и в коде, и в дальнейшем тестировании.
Логика работы
Так как это простой калькулятор, то поступим так:
- Сделаем поле ввода для первого числа.
- Под ним разместим 4 кнопки с математическими действиями.
- Потом сделаем поле ввода для второго числа.
- И внизу будет кнопка «Посчитать».
Размещаем кнопки и поля ввода на странице
Разместим кнопки с полями на странице, а потом будем писать скрипт.
Калькулятор + — x :
Посчитать
Обрабатываем нажатия на кнопки математических действий
Сейчас у нас есть 4 кнопки, но нажимать их бесполезно — всё равно ничего не произойдёт, потому что нет обработчиков нажатий. Но что нам прописывать в обработчике?
Первый вариант — привязать к каждой кнопке свою функцию, а потом для каждой операции выполнять свои действия внутри этого обработчика. Но раз у нас есть кнопка «Посчитать», то нам придётся при нажатии на неё из этих четырёх функций вытаскивать действие и нужные команды, запоминать выбранное и как-то использовать в вычислениях. Сложно и громоздко.
Второй вариант — просто записывать в какую-то переменную, какая кнопка была нажата. А потом, при нажатии «Посчитать», просто смотреть в эту переменную и выполнять соответствующее действие. Так и поступим.
Воспользуемся хитростью, про которые многие забывают: в обработчике onclick необязательно писать только функцию — туда можно отправить любую JS-команду. Главное, не забыть потом в скрипте предусмотреть эту переменную, которую мы используем.
Источник: thecode.media
Написание простейшего калькулятора в Python 3
Язык программирования Python является отличным инструментом для обработки чисел и математических выражений. На основе этого качества можно создавать полезные программы.
В данном руководстве вам предлагается полезное упражнение: попробуйте написать простую программу командной строки для выполнения вычислений. Итак, в данном руководстве вы научитесь создавать простейший калькулятор в Python 3.
В руководстве используются математические операторы, переменные, условные выражения, функции.
Требования
Для выполнения руководства нужно установить Python 3 на локальную машину и развернуть среду разработки. Все необходимые инструкции можно найти здесь:
- Настройка локальной среды разработки для Python 3 в CentOS 7
- Настройка локальной среды разработки для Python 3 в Windows 10
- Настройка локальной среды разработки для Python 3 в Mac OS X
- Настройка локальной среды разработки для Python 3 в Ubuntu 16.04
1: Строка ввода
Для начала нужно написать строку ввода, с помощью которой пользователи смогут вводить данные для вычислений в калькуляторе.
Для этого используйте встроенную функцию input(), которая принимает сгенерированный пользователем ввод с клавиатуры. В круглых скобках функции input() можно передать строку. Пользовательскому вводу нужно присвоить переменную.
В данной программе пользователь сможет вводить два числа. Запрашивая ввод, нужно добавить пробел в конце строки, чтобы отделить ввод пользователя от строки программы.
number_1 = input(‘Enter your first number: ‘)
number_2 = input(‘Enter your second number: ‘)
Прежде чем запустить программу, сохраните файл. К примеру, назовём программу calculator.py. теперь можно запустить программу в окне терминала в среде разработки с помощью команды:
Программа предложит вам ввести два числа:
Enter your first number: 5
Enter your second number: 7
На данный момент калькулятор принимает любые входные данные, не ограничиваясь числами: слова, символы, пробелы, даже enter. Это происходит потому, что функция input() принимает данные как строки и не знает, что в данном случае нужны только числа.
Чтобы программа могла выполнять математические вычисления, она не должна принимать никаких данных, кроме чисел.
В зависимости от предназначения калькулятора, программа может преобразовывать строки функции input() в целые числа или в числа с плавающей точкой. В данном случае целые числа подходят больше. Функцию input() нужно передать внутри функции int(), чтобы преобразовать ввод в целое число.
number_1 = int(input(‘Enter your first number: ‘))
number_2 = int(input(‘Enter your second number: ‘))
Теперь попробуйте ввести два целых числа:
Enter your first number: 23
Enter your second number: 674
Все работает без ошибок. Однако если вы введёте символы, пробелы или буквы, программа вернёт ошибку:
Enter your first number: hello
Traceback (most recent call last):
File «testing.py», line 1, in
number_1 = int(input(‘Enter your first number: ‘))
ValueError: invalid literal for int() with base 10: ‘hello’
Итак, вы написали строку для ввода данных в программу.
Примечание: Попробуйте самостоятельно преобразовать входные данные в числа с плавающей точкой.
2: Добавление операторов
Теперь нужно добавить четыре базовых оператора: + (сложение), – (вычитание), * (умножение) и / (деление).
Программу лучше разрабатывать постепенно, чтобы иметь возможность протестировать её на каждом этапе.
Сначала добавьте оператор сложения. Поместите два числа в print, чтобы калькулятор отображал результат.
number_1 = int(input(‘Enter your first number: ‘))
number_2 = int(input(‘Enter your second number: ‘))
print(number_1 + number_2)
Запустите программу и попробуйте сложить два числа:
Enter your first number: 8
Enter your second number: 3
11
Теперь можно немного усложнить программу. Пусть кроме результата калькулятор также отображает числа, введенные пользователем.
number_1 = int(input(‘Enter your first number: ‘))
number_2 = int(input(‘Enter your second number: ‘))
print(‘<> + <> = ‘.format(number_1, number_2))
print(number_1 + number_2)
Снова запустите программу и попробуйте ввести какие-нибудь числа:
Enter your first number: 90
Enter your second number: 717
90 + 717 =
807
Теперь пользователь сможет убедиться, что ввел правильные числа.
На данном этапе можно добавить остальные операторы, используя такой же формат:
number_1 = int(input(‘Enter your first number: ‘))
number_2 = int(input(‘Enter your second number: ‘))
# Addition
print(‘<> + <> = ‘.format(number_1, number_2))
print(number_1 + number_2)
# Subtraction
print(‘<> — <> = ‘.format(number_1, number_2))
print(number_1 — number_2)
# Multiplication
print(‘<> * <> = ‘.format(number_1, number_2))
print(number_1 * number_2)
# Division
print(‘<> / <> = ‘.format(number_1, number_2))
print(number_1 / number_2)
Теперь калькулятор может выполнять математические вычисления при помощи операторов +, -, * и /. Далее нужно ограничить количество операций, которые программа может выполнить за один раз.
3: Добавление условного оператора
Добавьте в начало программы calculator.py небольшое описание с перечнем доступных операций. Выбрав один из операторов, пользователь сообщит программе, что именно ей нужно будет делать.
»’
Please type in the math operation you would like to complete:
+ for addition
— for subtraction
* for multiplication
/ for division
»’
Примечание: На самом деле здесь можно использовать любые символы (например, 1 для сложения, b для вычитания и так далее).
Передайте строку внутри функции input() и присвойте переменную значению ввода (к примеру, это будет переменная operation).
operation = input(»’
Please type in the math operation you would like to complete:
+ for addition
— for subtraction
* for multiplication
/ for division
»’)
number_1 = int(input(‘Enter your first number: ‘))
number_2 = int(input(‘Enter your second number: ‘))
print(‘<> + <> = ‘.format(number_1, number_2))
print(number_1 + number_2)
print(‘<> — <> = ‘.format(number_1, number_2))
print(number_1 — number_2)
print(‘<> * <> = ‘.format(number_1, number_2))
print(number_1 * number_2)
print(‘<> / <> = ‘.format(number_1, number_2))
print(number_1 / number_2)
В эту строку пользователь может ввести любой из предложенных символов, но ничего не произойдёт. Чтобы программа работала, нужно добавить условный оператор. Оператор if будет отвечать за сложение, три оператора elif – за остальные операции; оператор else будет возвращать ошибку, если вместо предложенных операторов пользователь ввёл другой символ.
operation = input(»’
Please type in the math operation you would like to complete:
+ for addition
— for subtraction
* for multiplication
/ for division
»’)
number_1 = int(input(‘Enter your first number: ‘))
number_2 = int(input(‘Enter your second number: ‘))
if operation == ‘+’:
print(‘<> + <> = ‘.format(number_1, number_2))
print(number_1 + number_2)
elif operation == ‘-‘:
print(‘<> — <> = ‘.format(number_1, number_2))
print(number_1 — number_2)
elif operation == ‘*’:
print(‘<> * <> = ‘.format(number_1, number_2))
print(number_1 * number_2)
elif operation == ‘/’:
print(‘<> / <> = ‘.format(number_1, number_2))
print(number_1 / number_2)
else:
print(‘You have not typed a valid operator, please run the program again.’)
Итак, сначала программа предлагает пользователю ввести символ операции. Затем она запрашивает два числа. После этого она отображает пользовательский ввод и результат вычислений. Например, пользователь вводит *, затем 58 и 40.
Please type in the math operation you would like to complete:
+ for addition
— for subtraction
* for multiplication
/ for division
*
Please enter the first number: 58
Please enter the second number: 40
58 * 40 =
2320
Если же на первый запрос программы пользователь введёт символ %, он получит ошибку.
На данный момент программа выполняет все необходимые вычисления. Однако чтобы выполнить другую операцию, программу придётся перезапустить.
4: Определение функций
Чтобы программу не пришлось перезапускать после каждого обработанного примера, нужно определить несколько функций. Для начала поместим весь существующий код в функцию calculate() и добавим в программу ещё один слой. Чтобы программа запускалась, нужно добавить функцию в конец файла.
# Определение функции
def calculate():
operation = input(»’
Please type in the math operation you would like to complete:
+ for addition
— for subtraction
* for multiplication
/ for division
»’)
number_1 = int(input(‘Please enter the first number: ‘))
number_2 = int(input(‘Please enter the second number: ‘))
if operation == ‘+’:
print(‘<> + <> = ‘.format(number_1, number_2))
print(number_1 + number_2)
elif operation == ‘-‘:
print(‘<> — <> = ‘.format(number_1, number_2))
print(number_1 — number_2)
elif operation == ‘*’:
print(‘<> * <> = ‘.format(number_1, number_2))
print(number_1 * number_2)
elif operation == ‘/’:
print(‘<> / <> = ‘.format(number_1, number_2))
print(number_1 / number_2)
else:
print(‘You have not typed a valid operator, please run the program again.’)
# Вызов функции calculate() вне функции
calculate()
Создайте ещё одну функцию, состоящую из условных операторов. Этот блок кода позволит пользователю выбрать: продолжить работу с программой или завершить её. В данном случае операторов будет три: один if, один elif и один else для обработки ошибок.
Пусть функция называется again(). Добавьте её в конец блока def calculate():
.
# Определение функции again()
def again():
# Ввод пользователя
calc_again = input(»’
Do you want to calculate again?
Please type Y for YES or N for NO.
»’)
# Если пользователь вводит Y, программа запускает функцию calculate()
if calc_again == ‘Y’:
calculate()
# Если пользователь вводит N, программа попрощается и завершит работу
elif calc_again == ‘N’:
print(‘See you later.’)
# Если пользователь вводит другой символ, программа снова запускает функцию again()
else:
again()
# Вызов calculate()
calculate()
Также можно устранить чувствительность к регистру: буквы y и n должны восприниматься так же, как Y и N. Для этого добавьте функцию строки str.upper():
.
def again():
calc_again = input(»’
Do you want to calculate again?
Please type Y for YES or N for NO.
»’)
# Accept ‘y’ or ‘Y’ by adding str.upper()
if calc_again.upper() == ‘Y’:
calculate()
# Accept ‘n’ or ‘N’ by adding str.upper()
elif calc_again.upper() == ‘N’:
print(‘See you later.’)
else:
again()
.
Теперь нужно добавить функцию again() в конец функции calculate(), чтобы программа запускала код, который спрашивает пользователя, хочет ли он продолжить работу.
def calculate():
operation = input(»’
Please type in the math operation you would like to complete:
+ for addition
— for subtraction
* for multiplication
/ for division
»’)
number_1 = int(input(‘Please enter the first number: ‘))
number_2 = int(input(‘Please enter the second number: ‘))
if operation == ‘+’:
print(‘<> + <> = ‘.format(number_1, number_2))
print(number_1 + number_2)
elif operation == ‘-‘:
print(‘<> — <> = ‘.format(number_1, number_2))
print(number_1 — number_2)
elif operation == ‘*’:
print(‘<> * <> = ‘.format(number_1, number_2))
print(number_1 * number_2)
elif operation == ‘/’:
print(‘<> / <> = ‘.format(number_1, number_2))
print(number_1 / number_2)
else:
print(‘You have not typed a valid operator, please run the program again.’)
# Добавление функции again() в calculate()
again()
def again():
calc_again = input(»’
Do you want to calculate again?
Please type Y for YES or N for NO.
»’)
if calc_again.upper() == ‘Y’:
calculate()
elif calc_again.upper() == ‘N’:
print(‘See you later.’)
else:
again()
calculate()
Запустите программу в терминале с помощью команды:
Теперь программу не нужно перезапускать.
5: Дополнительные действия
Написанная вами программа полностью готова к работе. Однако есть ещё много дополнений, которые при желании можно внести в код. Например, вы можете написать приветственное сообщение и добавить его в начало кода:
def welcome():
print(»’
Welcome to Calculator
»’)
.
# Затем нужно вызвать функции
welcome()
calculate()
Также можно добавить в программу больше функций для обработки ошибок. К примеру, программа должна продолжать работу даже если пользователь вводит слово вместо числа. На данный момент это не так: программа выдаст пользователю ошибку и прекратит работу.
Кроме того, если при выборе оператора деления (/) пользователь выбирает знаменатель 0, он должен получить ошибку:
ZeroDivisionError: division by zero
Для этого нужно написать исключение с помощью оператора try … except.
Программа ограничена 4 операторами, но вы можете расширить этот список:
.
operation = input(»’
Please type in the math operation you would like to complete:
+ for addition
— for subtraction
* for multiplication
/ for division
** for power
% for modulo
»’)
.
# Для возведения в степень и обработки модуля нужно добавить в код условные операторы.
Также в программу можно добавить операторы цикла.
Существует много способов для настройки обработки ошибок и улучшения каждого проекта. При этом всегда важно помнить, что не существует единственно правильного способа решить ту или иную проблему.
Заключение
Теперь вы знаете, как написать простейший калькулятор. После выполнения руководства вы можете самостоятельно добавить новые функции программы.
Источник: www.8host.com