Написать программу решения системы двух линейных уравнений с двумя неизвестными и вывода его корней на экран. A1X + B1Y = H1 A2X + B2Y = H2. Алгоритм решения реализовать в виде процедуры. Входные параметры процедуры — коэффициенты и свободные члены, выходные — решения X и Y.
Код к задаче: «Написать программу решения системы двух линейных уравнений с двумя неизвестными и вывода его корней на экран.»
Листинг программы
uses crt; procedure Korni(a1,b1,c1,a2,b2,c2:real;var x,y:real); begin if abs(a1*b2-a2*b1) b2:=b1+b2*(-a1/a2); c2:=c1+c2*(-a1/a2); y:=c2/b2; x:=(c1-b1*y)/a1; end; end; var a1,b1,h1,a2,b2,h2,x,y:real; begin clrscr; writeln(‘Введите коэффициенты первого уравнения:’); readln(a1,b1,h1); writeln(‘Введите коэффициенты второго уравнения:’); readln(a2,b2,h2); Korni(a1,b1,h1,a2,b2,h2,x,y); writeln(‘Корни системы:’); write(‘x=’,x:0:2,’ y=’,y:0:2); readln; end.
Источник: studassistent.ru
Решение систем уравнений методом подстановки
Решаем систему линейных алгебраических уравнений с Python-пакетом scipy.linalg (не путать с numpy.linalg)

Аппарат линейной алгебры применяют в самых разных областях — в линейном программировании, эконометрике, в естественных науках. Отдельно отмечу, что этот раздел математики востребован в машинном обучении. Если, например, вам нужно поработать с матрицами и векторами, то, вполне возможно, на каком-то шаге вам придётся решать систему линейных алгебраических уравнений (СЛАУ).
СЛАУ — мощный инструмент моделирования процессов. Если некая хорошо изученная модель на основе СЛАУ годится для формализации задачи, то с высокой вероятностью её можно будет решить. А вот насколько быстро — это зависит от вашего инструментария и вычислительных мощностей.
Я расскажу про один из таких инструментов — Python-пакет scipy.linalg из библиотеки SciPy, который позволяет быстро и эффективно решать многие задачи с использованием аппарата линейной алгебры.
В этом туториале вы узнаете:
- как установить scipy.linalg и подготовить среду выполнения кода;
- как работать с векторами и матрицами с помощью NumPy;
- почему scipy.linalg лучше, чем numpy.linalg;
- как формализовать задачи с использованием систем линейных алгебраических уравнений;
- как решать СЛАУ с помощью scipy.linalg (на реальном примере).
Когда речь идёт о математике, изложение материала должно быть последовательным — таким, чтобы одно следовало из другого. Эта статья не исключение: сначала будет много подготовительной информации и только потом мы перейдём непосредственно к делу.
Если готовы к этому — приглашаю под кат. Хотя, честно говоря, некоторые разделы можно пропускать — например, основы работы с векторами и матрицами в NumPy (если вы хорошо знакомы с ним).
Python для самых маленьких. Линейные уравнения. Решение задач
Установка scipy.linalg
SciPy — это библиотека Python с открытым исходным кодом для научных вычислений: решение СЛАУ, оптимизация, интеграция, интерполяция и обработка сигналов. Помимо linalg, она содержит несколько других пакетов — например, NumPy, Matplotlib, SymPy, IPython и pandas.
Среди прочего, scipy.linalg содержит функции для с работы с матрицами — вычисление определителя, инверсия, вычисление собственных значений и векторов, а также сингулярное разложение.
Чтобы использовать scipy.linalg, вам необходимо установить и настроить библиотеку SciPy. Это можно сделать с помощью дистрибутива Anaconda, а также системы управления пакетами и инсталлятора Conda.
Для начала подготовьте среду выполнения для библиотеки:
$ conda create —name linalg $ conda activate linalg
Установите необходимые пакеты:
(linalg) $ conda install scipy jupyter
Эта команда может работать долго. Не пугайтесь!
Я предлагаю использовать Jupyter Notebook для запуска кода в интерактивной среде. Это не обязательно, но лично мне он облегчает работу.
Перед открытием Jupyter Notebook вам необходимо зарегистрировать экземпляр conda linalg, чтобы использовать его в качестве ядра при создании ноутбука. Для этого выполните следующую команду:
(linalg) $ python -m ipykernel install —user —name linalg
Теперь можно открыть Jupyter Notebook:
$ jupyter notebook
Когда он загрузится в вашем браузере, создайте новый notebook, нажав New → linalg:
Чтобы убедиться, что установка библиотеки SciPy прошла успешно, введите в ноутбуке:
>>> In [1]: import scipy
NumPy для работы с векторами и матрицами (куда же без него)
Сложно переоценить роль векторов и матриц при решении технических задач и, в том числе, задач машинного обучения.
NumPy — это наиболее популярный пакет для работы с матрицами и векторами в Python. Часто его применяют в сочетании с scipy.linalg. Чтобы начать работу с матрицами и векторами, нужно импортировать пакет NumPy:
>>> In [2]: import numpy as np
Для представления матриц и векторов NumPy использует специальный тип, называемый ndarray. Чтобы создать объект ndarray, вы можете использовать array ().
Например, вам нужно создать следующую матрицу:
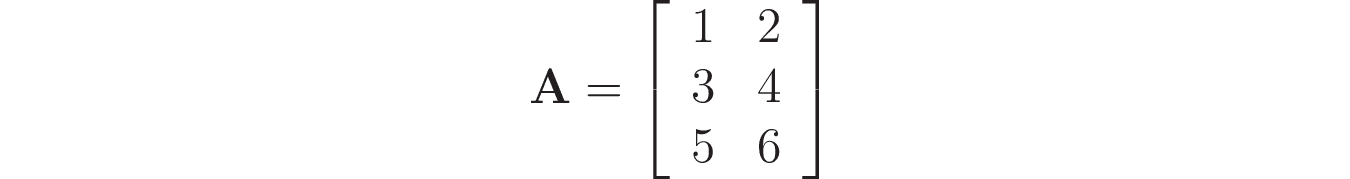
Создадим матрицу как набор вложенных списков (векторов-строк):
>>> In [3]: A = np.array([[1, 2], [3, 4], [5, 6]]) . A Out[3]: array([[1, 2], [3, 4], [5, 6]])
Заметьте, что приведённый выше вывод (Outp[3]) достаточно наглядно показывает получившуюся матрицу.
И ещё: все элементы матрицы должны и будут иметь один тип. Это можно проверить с помощью dtype.
>>> In [4]: A.dtype Out[4]: dtype(‘int64’)
Здесь элементы являются целыми числами, поэтому их общий тип по умолчанию — int64. Если бы среди них было хотя бы одно число с плавающей точкой, все элементы получили бы тип float64:
>>> In [5]: A = np.array([[1.0, 2], [3, 4], [5, 6]]) . A Out[5]: array([[1., 2.], [3., 4.], [5., 6.]]) In [6]: A.dtype Out[6]: dtype(‘float64’)
Чтобы вывести на экран размерность матрицы, можно использовать метод shape:
>>> In [7]: A.shape Out[7]: (3, 2)
Как и ожидалось, размерность матрицы A 3×2, то есть A имеет три строки и два столбца.
При работе с матрицами часто приходится использовать операцию транспонирования, которая столбцы превращает в строки и наоборот. Чтобы транспонировать вектор или матрицу (представленную объектом типа ndarray), вы можете использовать .transpose () или .T. Например:
>>> In [8]: A.T Out[8]: array([[1., 3., 5.], [2., 4., 6.]])
Чтобы создать вектор, также можно использовать.array(), передав туда список значений в качестве аргумента:
>>> In [9]: v = np.array([1, 2, 3]) . v Out[9]: array([1, 2, 3])
По аналогии с матрицами, используем .shape(), чтобы вывести на экран размерность вектора:
>>> In [10]: v.shape Out[10]: (3,)
Заметьте, что она выглядит как (3,), а не как (3, 1) или (1, 3). Разработчики NumPy решили сделать отображение размерности векторов так же, как в MATLAB.
Чтобы получить на выходе размерность (1, 3), нужно было бы создать вот такой массив:
>>> In [11]: v = np.array([[1, 2, 3]]) . v.shape Out[11]: (1, 3)
Для (3, 1) — вот такой:
>>> In [12]: v = np.array([[1], [2], [3]]) . v.shape Out[12]: (3, 1)
Как видите, они не идентичны.
Часто возникает задача из вектора-строки сделать вектор-столбец. Как вариант, можно сначала создать вектор-строку, а потом использовать .reshape() для его преобразования в столбец:
>>> In [13]: v = np.array([1, 2, 3]).reshape(3, 1) . v.shape Out[13]: (3, 1)
В приведённом выше примере мы использовали .reshape() для получения вектора-столбца с размерностью (3, 1) из вектора с размерностью(3,). Стоит отметить, что .reshape() делает преобразование с учётом того, что количество элементов (100% заполненных мест) в массиве с новой размерностью должно быть равно количеству элементов в исходном массиве.
В практических задачах часто требуется создавать матрицы, полностью состоящие из нулей, единиц или случайных чисел. Для этого NumPy предлагает несколько удобных функций, о которых я расскажу в следующем разделе.
Заполнение массивов данными
NumPy позволяет быстро создавать и заполнять массивы. Например, чтобы создать массив, заполненный нулями, можно использовать .zeros():
>>> In [15]: A = np.zeros((3, 2)) . A Out[15]: array([[0., 0.], [0., 0.], [0., 0.]])
В качестве аргумента .zeros() нужно указать размерность массива, упакованную в кортеж (перечислить значения через запятую и обернуть это в круглые скобки). Элементы созданного массива получат тип float64.
Точно так же, для создания массивов из единиц можно использовать .ones ():
>>> In [16]: A = np.ones((2, 3)) . A Out[16]: array([[1., 1., 1.], [1., 1., 1.]])
Элементы созданного массива также получат тип float64.
Создать массив, заполненный случайными числами, поможет .random.rand():
>>> In [17]: A = np.random.rand(3, 2) . A Out[17]: array([[0.8206045 , 0.54470809], [0.9490381 , 0.05677859], [0.71148476, 0.4709059 ]])
Говоря точнее, метод .random.rand() возвращает массив с псевдослучайными значениями (от 0 до 1) из множества, сгенерированного по закону равномерного распределения. Обратите внимание, что в отличие от .zeros() и .ones(), .random.rand () на вход принимает не кортеж, а просто два значения через запятую.
Чтобы получить массив с псевдослучайными значениями, взятыми из множества, сгенерированного по закону нормального распределения с нулевым средним и единичной дисперсией, вы можете использовать .random.randn():
>>> In [18]: A = np.random.randn(3, 2) . A Out[18]: array([[-1.20019512, -1.78337814], [-0.22135221, -0.38805899], [ 0.17620202, -2.05176764]])
Почему scipy.linalg лучше, чем numpy.linalg
NumPy имеет встроенный модуль numpy.linalg для решения некоторых задач, связанных с аппаратом линейной алгебры. Обычно scipy.linalg рекомендуют использовать по следующим причинам:
-
В официальной документации сказано, что scipy.linalg содержит все функции numpy.linalg, а также дополнительные функции, не входящие в numpy.linalg.
В следующем разделе мы применим scipy.linalg для работы с системами линейных алгебраических уравнений. Наконец-то практика!
Формализация и решение задач с scipy.linalg
Пакет scipy.linalg может стать полезным инструментом для решения транспортной задачи, балансировки химических уравнений и электрических нагрузок, полиномиальной интерполяции и так далее.
В этом разделе вы узнаете, как использовать scipy.linalg.solve() для решения СЛАУ. Но прежде чем приступить к работе с кодом, займёмся формализацией задачи и далее рассмотрим простой пример.
Система линейных алгебраических уравнений — это набор из m уравнений, n переменных и вектора свободных членов. Прилагательное «линейных» означает, что все переменные имеют первую степень. Для простоты рассмотрим СЛАУ, где m и n равны 3:
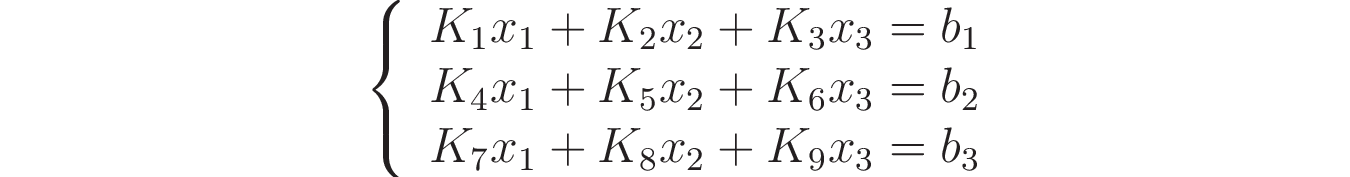
Есть ещё одно требование к «линейности»: коэффициенты K₁ … K₉ и вектор b₁ … b₃ должны быть константами (в математическом смысле этого слова).
В реальных задачах СЛАУ обычно содержат большое количество переменных, что делает невозможным решение систем вручную. К счастью, такие инструменты, как scipy.linalg, могут выполнить эту тяжелую работу.
Задача 1
Написание программы для решения системы уравнений методом сеток

Задание: Написать программу, которая решала бы методом сеток следующую систему уравнений:
a1(x,y)*d 2 U/dx 2 + a2(x,y)*d 2 U/dxdy+ a3(x,y)*d 2 U/dy 2 + b1(x,y)*dU/dx+ b2(x,y)*dU/dy+c(x,y)*U(x,y)=f(x,y) ;
Рассчитать погрешность метода.
Составить три тестовых примера для программы.
Пользователь задаёт прямоугольную область, на которой применяется метод сеток через координаты левого нижнего (a0,b0) и правого верхнего (a,b) углов области , а также количество узлов сетки по x и y (Nx,Ny).
Программой вычисляется шаг сетки (hx и hy) и формируется матрица Size*Size+1, где Size – количество точек сетки, то есть Nx*Ny. Матрица формируется следующим образом: для всех внутренних узлов сетки все виды производных можно приближённо записать через соседние точки:
Таким образом, эллиптическое уравнение для каждой из внутренних точек можно переписать относительно соседних точек в следующем виде:
Получается уравнений столько же, сколько и внутренних точек, но с Size неизвестными. Недостающие уравнения получаем из краевых условий.
Решаем полученную матрицу методом Гаусса и получаем вектор со значениями функции в узлах сетки.
1. U(x,y) = x 3 + y 3 ;
В программу забиваем следующие параметры:
f(x,y) = a1(x,y)*(6*x + y*y*y) + a2(x,y)*(3*x*x + 3*y*y) + a3(x,y)*(x*x*x + 6*y) +
+ b1(x,y)*(3*x*x+y*y*y) + b2(x,y)*(x*x*x + 3*y*y) + c(x,y)*(x*x*x + y*y*y).
Q1(x) = x*x*x + b0*b0*b0.
Q2(x) = x*x*x + bn*bn*bn.
Q3(y) = y*y*y + a0*a0*a0.
Q4(y) = y*y*y + an*an*an.
Источник: vunivere.ru