Если алгебраическое уравнение записано в виде (x=varphi left(x right)), то при выполнении определенных условий решение уравнения (приближенное) может быть найдено методом последовательных приближений. Суть метода состоит в том, что n+1-е приближение для корня уравнения (x_) вычисляется на основе n-го приближения (x_) через соотношение: $$x_=varphi left(x_ right)$$ Дальше задается начальное условие для начального решения, проверяется выполнение условия возможности применения приближенного метода, а затем применяются итерационные формулы. Программа для решения уравнения (x^-5x+6=0) итерационным методом приведена ниже. Здесь надо обратить внимание, что для каждого из корней (x=2,x=3) построены свои схемы из-за того, что возникают ограничения на выполнение условий применимости итерационного алгоритма. Для первого корня уравнение представляем в виде: $$x=left(x^+6 right)/5$$ но условие: $$left|dvarphi /dx right| выполняется только на интервале: (left|x right| $$x=sqrt$$ и тогда указанное выше условие выполняется для (x>2,45) а значит интересующий нас корень попадает в указанный диапазон.
Научиться программировать — C# — «решение квадратного уравнения», разбор задачи (часть 1)
Мне нравится
- Умножение на два в степени
- Аргументы со значениями по умолчанию в С++
- Пример работы с потоками в С++
- Метод половинного деления в С++
Оставить комментарий
Вы должны быть авторизованы , чтобы оставить или оценить комментарий.
Новые записи
- Сравнение различных типов .
- Зачем нужна аналитика Вайл.
- Розкриття потужності ігров.
- Про сувенірну продукцію та.
- Защита зрения: контактные .
- Про обладнання для шкільни.
- Сила настільних ігор для к.
- Як матраци Sleep Fly забез.
- Что такое портативная элек.
- Какой интернет магазин пла.
Новые комментарии
- Я нашел работу уже на посл
- Наклон шрифта удобно и точ
- И что это значит? совершен
- Спасибо. Крутые советы!
- интерестно
- «Сделайте пожалуйста
- Ну вот — «бессмысленн
- Бред. Выкладывать данные н
- На каком основании вы гово
- Только что придумал идею д
Популярные записи
- Гостовские чертежные рамки.
- 72 образца характеристик н.
- Чертежные шрифты студентам.
- Миллиметровка, система коо.
- Титульный лист курсовой ра.
- Таблица производных и инте.
- Построение поверхностей
- Пишем характеристику студе.
- Заявление на отчисление и .
- Пишем отзыв руководителя
Новые объявления
- Чем отличаются услуги грам.
- Серебряное мужское кольцо .
- Особенности и разновидност.
- Почему и когда нужен аудит.
- Быстрая покупка бикоина на.
- Не важно где ты находишься.
- Неожиданная причина почему.
- Как уберечь себя и свое пр.
- Несколько советов покупате.
- Доставка воды как бизнес
Источник: studlab.com
Java — урок 5.4 (Практика — решаем квадратное уравнение)
Как написать программу решения дифференциального уравнения… ( C++ )
Для численного решения обыкновенных дифференциальных уравнений различают задачи с начальными условиями (ЗНУ) и граничными условиями (ЗГУ).
Дело в том, что для полного определения искомой функции одного уравнения недостаточно. При определении первообразной из производной функции мы получим множество решений, отличающихся друг от друга свободным членом (константой С).
Поэтому, для однозначного определения данной константы С, у искомой функции должны задаваться еще граничные условия, указывающие, что делается на концах исследуемого интервала, и/или начальные условия, описывающие значение функции
в начальный момент (t = 0). Совокупность граничных и начальных условий называется краевыми условиями.
Для численного решения обыкновенных дифференциальных уравнений применяют метод Рунге-Кутта, с наиболее часто используемым 4-ым порядком точности. Давайте рассмотрим программную реализацию данного метода Рунге-Кутта, и Вы увидите, что написать программу для решения дифференциального уравнения не составляет особого труда.
Вариант решения задачи рассмотрю на следующем примере:
Условия задачи:
Пусть выстрел из орудия произведен с начальной скоростью V0, под углом к горизонту α, с высоты Н0 расположения орудия, т.к. в реальности огонь может вестись с холма или из капонира (т.е. ниже уровня земли).
Считаем, что снаряд имеет форму шара с радиусом r, изготовлен из материала, имеющего определенную плотность ρ.
Построить траекторию полета снаряда Y(x) ,
указать максимальную высоту полета Hk , дальность падения снаряда Xk и время полета tk , построить график скорости V(t) на отрезке [0,tk].
Таким образом, исходные данные, которые пользователь может задать на форме:
Начальная скорость V0, м/с2
Начальная высота H0, м
Угол выстрела α, ° (град)
Плотность материала ρ, кг/м3
Радиус r, м
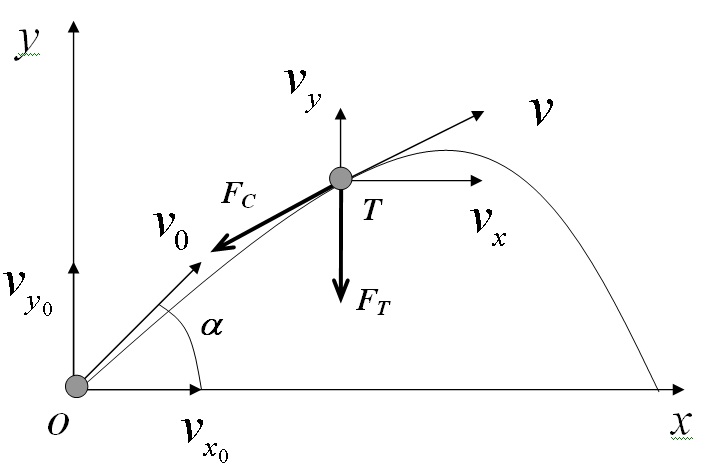
При построении математической модели условимся, что ось Оx системы координат направлена горизонтально в направлении выстрела, а ось Oy — вертикально вверх. Вектор скорости снаряда V(t) за время полета будет изменяться как по величине, так и по направлению, поэтому в модели рассматриваем его проекции на координатные оси. Горизонтальную составляющую скорости в момент времени t обозначим Vx(t), а вертикальную – Vy(t).
Пусть поверхность Земли плоская. Согласно законам механики, при сделанных предположениях движения тела в горизонтальном направлении является равномерным, а в вертикальном – равнозамедленным или равноускоренным с ускорением свободного падения g.
Если с силой тяжести FT все достаточно просто (она свой вектор не меняет ни по величине, ни по направлению), то сила лобового сопротивления FC , действующая на снаряд, пропорциональна квадрату скорости движения тела. Обозначим через FX и FY горизонтальную и вертикальную проекции вектора силы лобового сопротивления,
причем FX/F= VX/V, FY/F= VY/V.
Значение силы лобового сопротивления F= -b·V² (пропорционально квадрату скорости тела). Коэффициент b=0.5·C·S·ρ, где C – коэффициент лобового сопротивления (для многих задач баллистики C≈0.15), S – площадь поперечного сечения (S=πr²), ρ — плотность воздуха (ρ=1,29 кг/м3).
Решение поставленной задачи можно свести к решению системы дифференциальных уравнений
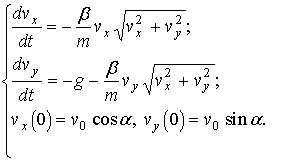
Метод Рунге-Кутта предполагает многократное вычисление значения производной искомой функции по имеющейся формуле (из уравнения), поэтому имеет смысл …
Код функций будет выглядеть так:
// функция Нахождение горизонтальной проекции скорости
//по первому уравнению системы
double Form1::fvx( double vy, double vx )
<
return -b*vx*sqrt(vx*vx+vy*vy) / m;
>
// функция Нахождение вертикальной проекции скорости
//по второму уравнению системы
double Form1::fvy( double vy, double vx )
<
return -b*vy*sqrt(vx*vx+vy*vy) / m — g;
>
Шаг интегрирования у меня задается на форме.
Сейчас нам предстоит вычислить значения нескольких функций (Vx, Vy, V ) в точках интервала с шагом. В моем примере у интервала задано начало х=0, а конечная точка интервала будет определена в процессе вычисления ( высота полета ядра стала <=0).
Результаты вычислений помещаются в массивы…
Код процедуры будет выглядеть так:
Void Form1::Runge_Kutta(void)
double k1,k2,k3,k4, l1,l2,l3,l4;
pY[0]=H; pX[0]=0; pt[0]=0; //массивы-координаты: высота, дальность и время
pVx[0]=Vx; pVy[0]=Vy; pV[0]=V; //массивы- скорости: проекции на
//горизонталь и вертикаль и полная скорость (величина вектора)
bool vzbool=true;//взлет
int i=1;
//расчет по модели и заполнение массивов
while( (pY[i-1]>-0.00001 || vzbool) i <
pt[i] =pt[i-1]+_h;
k1 = _h * fvx( pVy[i-1], pVx[i-1]);
l1 = _h * fvy( pVy[i-1], pVx[i-1]);
k2 = _h * fvx( pVy[i-1]+l1/2, pVx[i-1]+k1/2 );
l2 = _h * fvy( pVy[i-1]+l1/2, pVx[i-1]+k1/2 );
k3 = _h * fvx( pVy[i-1]+l2/2, pVx[i-1]+k2/2 );
l3 = _h * fvy( pVy[i-1]+l2/2, pVx[i-1]+k2/2 );
k4 = _h * fvx( pVy[i-1]+l3, pVx[i-1]+k3 );
l4 = _h * fvy( pVy[i-1]+l3, pVx[i-1]+k3 );
//вот собственно формула, определяющая метод Рунге-Кутта:
// получаем проекции скорости из предварительно полученных
//приближенных значений
pVx[i]=pVx[i-1] + (k1+2*k2+2*k3+k4)/6;
pVy[i]=pVy[i-1] + (l1+2*l2+2*l3+l4)/6;
pV[i] = sqrt( pVx[i]*pVx[i] + pVy[i]*pVy[i] ); //величина вектора скорости
//из проекций
pY[i]=pY[i-1]+pVy[i]*h;
pX[i]=pX[i-1]+pVx[i]*h; //пересчет координат
if(pY[i]>pY[i-1]) iMax=i; //сохранение номера узла с максимальной высотой
else vzbool=false;//падение
i++;
>
n=i-1; //количество реальных шагов
>
где:
int iMax; //узел с макс.высотой полета
double b; //коэф.пропорциональности Силы лобового сопротивления
double m; //масса ядра
double H; //уровень расположения орудия в момент выстрела
double V,Vx,Vy; //начальная скорость и ее проекции на оси
В результате работы этой подпрограммы произойдет численное решение задачи Коши для системы обыкновенных дифференциальных уравнений и будут получены значения функций Vx(ti), Vy(ti) в точках ti=i·h, i=1,2. ; h – шаг метода.
Как видим, после получения нового значения скорости Vx(ti)
рассчитывается координата X(ti)=X(ti-1)+h·Vx(ti), где h= ti-ti-1 = const.
Кроме того, параллельно рассчитывается значение высоты Y(ti)=Y(ti-1)+h·Vy(ti),
где h= ti-ti-1 = const по найденным значениям Vy(ti).
Когда будет получено значение Y(ti), вычисления заканчиваются
(немного модифицировано в условиях цикла while).
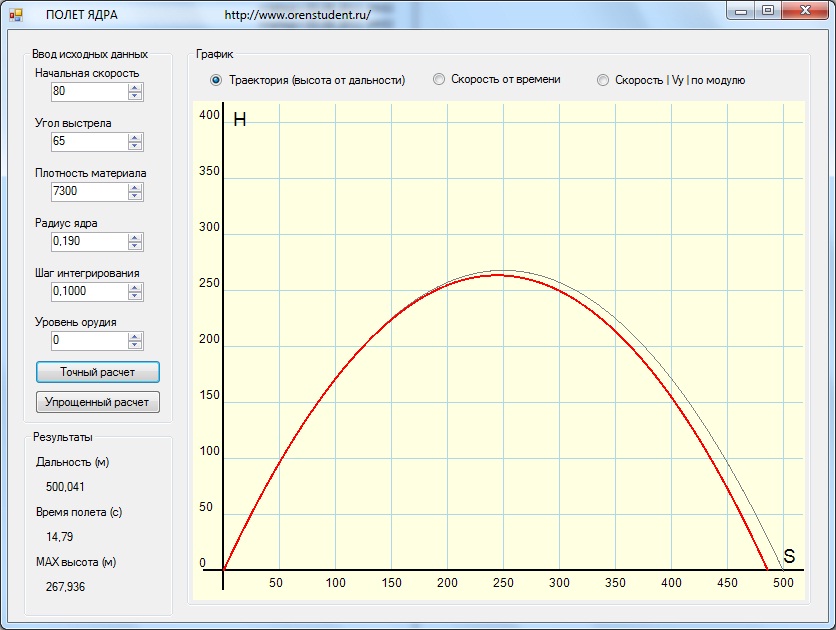
Кроме того, в программе интерполируются функции y(t), у(х) для нахождения более точных значений дальности и времени полета, а также максимальной высоты траектории. Полученные при интерполяции данные используем для построения траектории полета снаряда с более мелким шагом, например h=0,02 (сек).
Также в программе для сравнения проведен расчет по упрощенной модели, известной как модель Галилея, пренебрегая сопротивлением воздуха.
Желающим, УДАЛЕННО (или В ФОРМЕ РЕПЕТИТОРСТВА), объясню материал
на примере ИХ ВАРИАНТА ЗАДАНИЯ…
Исходный код с подробными комментариями – на Ваш носитель или e-mail.
Источник: orenstudent.ru
Исследовательская работа на тему: �«Исследование методов решения уравнений с помощью компьютерных программ
![]()

- Проблема : создать программу для автоматического решения уравнений
- Объект иследования : решение уравнений с помощью компьютера
- Предмет исследования : компьютерные программы
- Гипотеза: я считаю, что компьютерные программы для решения уравнений автоматизируют вычисление корней

Цель исследования : изучить и создать программы для автоматического вычисления корней уравнения.
Поставленная цель исследования предполагает решения ряда задач :
- Изучить различные виды уравнений
- Изучить способы решения уравнений
- Составить алгоритм решения уравнений
- Разработать вычислительные программы для решения уравнений
- Проанализировать результаты вычислений
- Сформулировать выводы и рекомендации по выбору программы для решения уравнений с помощью компьютера

- Методы исследования : сравнение и анализ, эксперимент, метод визуализации данных.
- Новизна исследования заключается в экспериментальной проверке компьютерных вычислений с помощью табличного процессора.
- Практическая значимость состоит в том, что созданные для проведения эксперимента программы можно будет использовать и в дальнейшем для нахождения корней уравнения

Задача № 1 Изучить различные виды уравнений
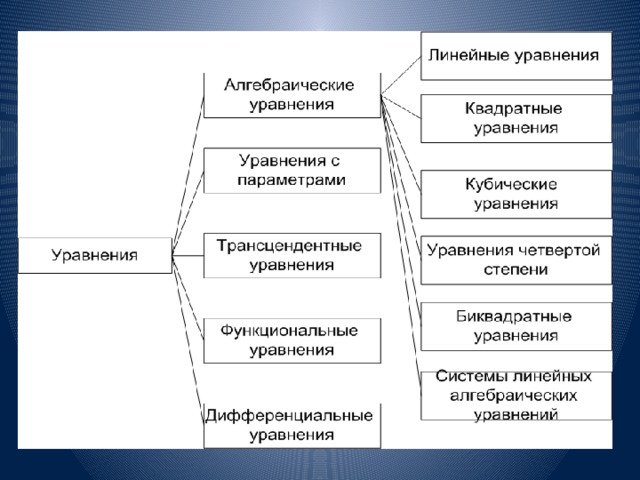

Задача № 2 Изучить способы решения уравнений

В своей работе, я решила остановиться на квадратных и биквадратных уравнениях, так как эти виды уравнений – самые распространенные. Они используются в таких науках , как алгебра, физика, геометрия и химия.
Способы решения квадратных уравнений:

- Общая формула для вычисления корней (нахождение дискриминанта)
- Использование прямой и обратной теоремы Виета
- Графический способ решения квадратных уравнений
Способы решения биквадратных уравнений:
Для решения биквадратного уравнения нужно сделать подстановку х 2 = t, найти корни t 1 и t 2 квадратного уравнения
аt 2 + bt + c = 0 и решить уравнения х 2 = t 1 и х 2 = t 2 . Они имеют решения лишь в случае, когда t 1,2 ≥ 0.

Задача № 3 Составить алгоритм решения уравнений
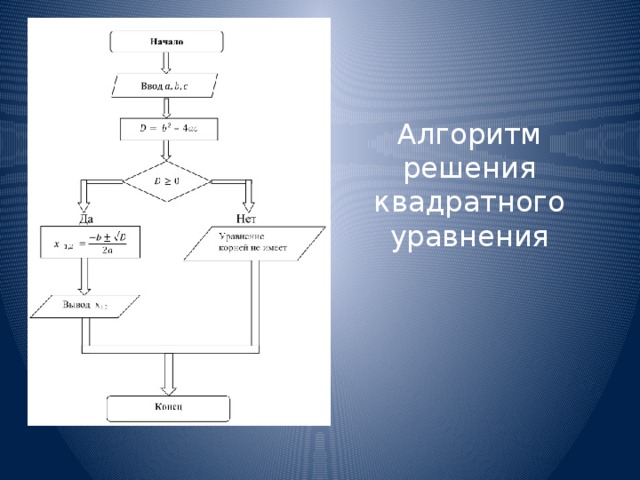
Алгоритм решения квадратного уравнения
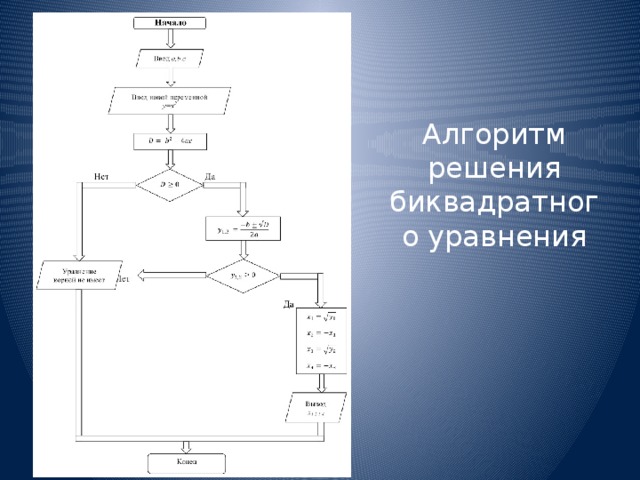
Алгоритм решения биквадратного уравнения

Задача № 4 Разработать вычислительные программы для решения уравнений

Программу которую я решила взять для решения уравнений – это MS Excel
Microsoft excel – программа для работы с электронными таблицами, созданная компанией Microsoft. Она представляет возможности экономико – статистических расчетов, графические инструменты

Технология решения квадратного уравнения в MS Excel
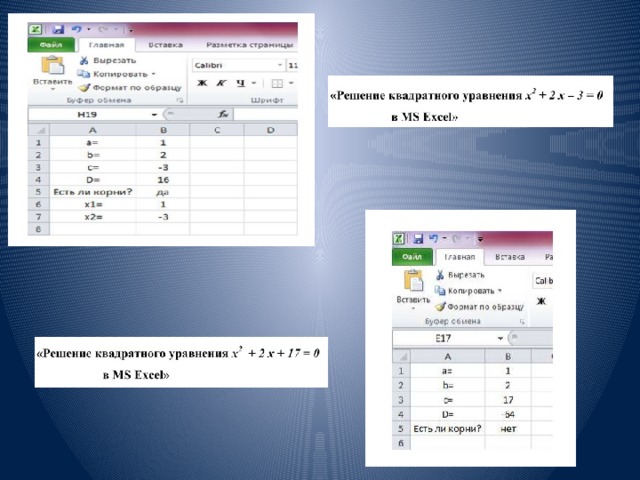

Технология решения биквадратного уравнения в MS Excel
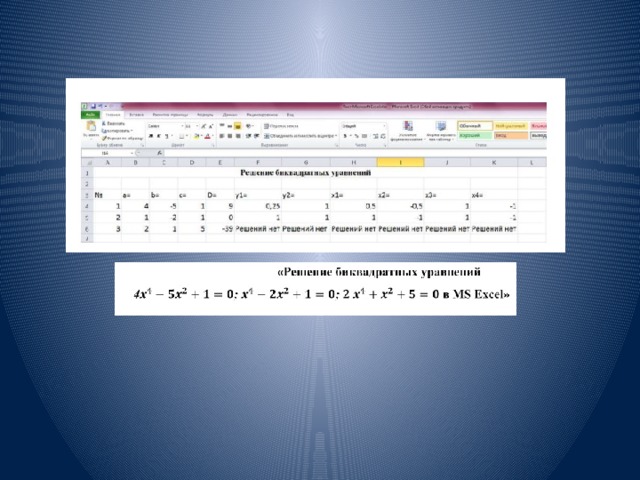

Задача № 5 Проанализировать результаты вычислений, сформулировать выводы.

Данная исследовательская работа позволила мне понять, что любую проблему можно решить. В школе нас этому учат. Мы знакомимся с различного рода задачами, и для их решения составляем уравнение. Также в школе нас знакомят с методами решения уравнений, открытыми великими математиками. Я научилась решать эти уравнения с помощью компьютерных технологий.
В итоге изучения материала о квадратных и биквадратных уравнениях я не только овладела применением алгоритмических предписаний к решению конкретных заданий, но и научилась использовать логические средства для обоснования решений в случаях, когда это необходимо.
Источник: kopilkaurokov.ru