Сейчас мы с вами попробуем написать программу на паскале для решения квадратных уравнений и неравенства. Перед тем как начать писать программу распишем ход его решения. Посмотрев на квадратное уравнение, мы увидим перед переменными коэффициенты и свободное число стоящее после них.
Назовем их k, m,n-свободное число, чтобы решить данное уравнение нужно найти дискриминант. Находится он по формуле приведенной ниже.
После того как найдем дискриминант нужно его проверить, если его значение больше нуля, то уравнение имеет два корня, если он равен нулю, то корень один, если же он отрицателен, то корней вообще нет. Далее мы находим сами корни по формуле приведенной ниже:
Вот мы и решили квадратное уравнение, теперь все это нужно написать на паскале.
Приступаем.
Var k, m, n :real;
x1, x2, D :real;
begin
Writeln(‘введите коэффициенты перед переменными и свободное число-’);
readln(k,m,n);
D:=sqr(m)-(4*k*n);
If D>0 then
begin
Pascal (Урок 4) Квадратное уравнение
x1:=(-m+sqrt(D))/2*k;
x2:=(-m-sqrt(D))/2*k;
writeln(‘Первый корень- ‘,x1,’ Второй корень- ‘,x2);
end else
if D=0 then
begin
x1:=(-m)/2*k;
writeln(‘ Корень — ‘,x1);
end else
writeln(‘ Корней нет ‘);
End.
Вот мы и написали программу для решения квадратных уравнений. В процессе написания программы я комментировал где, что происходит.
Теперь попробуем решить квадратные неравенства. Это гораздо сложнее, ведь придется учитывать много параметров. Но ничего, справимся. Итак, приступаем.
На картинке приведен один из видов неравенств, которые решаются практически так же, как и квадратное уравнение. Только здесь нужно учитывать знак k, после устного решения пишем программу
Var k ,m , n:real;
X1,x2,D:real;
Begin
Read(k,m,n);
D:=sqr(m)-4*k*n;
if D>=0 then begin
x1:=(-m+sqrt(D))/2*k;
x2:=(-m-sqrt(D))/2*k;
end;
if (D>0) and (k0) and (k>0) then writeln(‘X’,x1) else
if (D>0) and (k=0 ) and (m>0) then writeln(‘x>’,n/m) else
if (D>0) and (k=0 ) and (m if (k=0) and (m=0) then writeln(‘ Любое число ‘)else
writeln(‘ корней нет ‘);
end.
Этот пример иллюстрирует решение простого неравенства. Здесь нет ничего сложно, если не считать, что нужно учитывать каждую цифру.
Вот мы и рассмотрели квадратные уравнения и неравенства.
Источник: makarou.com
Вычислить корни квадратного уравнения
Вычислить корни квадратного уравнения ax2 + bx + x = 0 с заданными коэффициентами a, b и с (предполагается, что a ≠ 0 и что дискриминант уравнения неотрицателен).
Для решения данной задачи необходимо вспомнить формулу дискриминанта и корней квадратного уравнения:
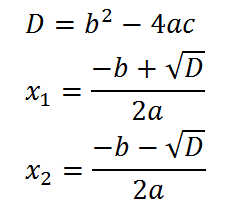
Pascal.Программа квадратное уравнение.
Формула дискриминанта и корней квадратного уравнения
Далее пишем программу:
program z_6; var a, b, c, D, x1, x2: real; begin write(‘a = ‘);read(a); write(‘b = ‘);read(b); write(‘c = ‘);read(c); D:=b*b-4*a*c; x1:=(-b + sqrt(D))/(2*a); x2:=(-b — sqrt(D))/(2*a); writeln(‘x1 = ‘, x1); writeln(‘x2 = ‘, x2); end.
Текст задачи:
Информатика. 10 класс. Базовый уровень. (Семакин И. Г., Хеннер Е. К., Шеина Т. Ю.)
Работа 3.1, Уровень 1, Задача №6
Источник: easyinformatics.ru
Как написать программу для решения квадратного уравнения в паскале
Введение.
Здравствуйте. На этот раз я хотел бы предложить вам исходник программы на языке PascalABC, которая решает квадратное уравнение, строя его на считанных с клавиатуры коэффициентов.

Задача.
Перед нами поставлена задача написать программу, которая будет искать решения квадратного уравнения по заранее указанным значениям его коэффициентов. Данное решение можно считать достаточно простым, использовать мы будем цикл IF. Для выполнения задачи необходимо считать данные в соответствующее количество переменных, затем найти значение дискриминанта, проверить больше, меньше, или равен ли он нулю. Далее в зависимости от результатов проверки высчитываются и выводятся корни, либо сообщение о том, что корней нет. Для ясности понимания к каждой строке кода приложены необходимые комментарии.
Код.
var a,b,c: real;
x1,x2,D: real;
begin
readln(a,b,c);
D := b*b — 4*a*c;
if D writeln(‘Корней нет’)
else if D=0 then begin
x1 := -b/2/a;
writeln(‘x1=x2=’,x1);
end
else begin
x1 := (-b-sqrt(D))/2/a;
x2 := (-b+sqrt(D))/2/a;
writeln(‘x1=’,x1,’ x2=’,x2);
end;
end.