Как написать программу для решения квадратного уравнения

1. Энциклопедический словарь юного математика [Текст] / Сост. А.П. Савин, гл. ред. Б.В. Гнеденко, ред. В.Д.

Белоусов и др. – 2-е изд., перераб. и доп. – М.: Педагогика, 1989. – 352с.

2. Смышляев В.К. Все о великих математиках [Текст] / В.К. Смышляев. – 2-е изд., перераб. и доп. – М.: Марийское книжное издательство, 1977. – 224 с.

3. Википедия – свободная энциклопедия. Квадратное уравнение [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Квадратное_уравнение.

Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений, неравенств и их систем.

Одна из основных целей изучения школьного курса математики заключается в овладении способами решения алгебраических уравнений второй степени и приводимых к ним уравнений. В школьном курсе изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.

Быстрый способ решения квадратного уравнения

Практически все, что окружает современного человека – это все так или иначе связано с математикой. Последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в дальнейшем данная тенденция сохранится. Решение многих практических задач сводится к решению различных видов уравнений. При этом актуальным является использование ЭВМ и специального ПО при решении уравнений.

Цель работы: Разработка программы нахождения корней уравнения второй степени в среде программирования Паскаль-ABC.

1) Ознакомиться с историей квадратных уравнений и методами их решения.

2) Освоить приемы программирования в интегрированной среде Паскаль-ABC.

3) Разработать алгоритм и блок-схему нахождения корней квадратных уравнений.

4) Создать программу нахождения корней и протестировать её.

Объект исследования: уравнения второй степени.

Предмет исследования: Паскаль-программа решения уравнений второй степени в среде Паскаль-ABC.

История квадратных уравнений и методы их решений

Необходимость решать уравнения не только первой степени, но и второй ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков, с развитием астрономии, военного дела и нуждами самой математики. Первые упоминания о способах решения уравнений, которые мы сейчас называем квадратными, относятся ко второму тысячелетию до н.э. Это эпоха расцвета Вавилона и Древнего Египта.

Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и полные квадратные уравнения. Правила решения этих уравнений, изложенные в вавилонских источниках, совпадает по существу с современными, но в этих текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?

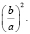
Герон Александрийский – греческий математик и механик. Время жизни предположительно отнесено ко второй половине I века н.э. «Метрика» Герона и извлечённые из неё «Геометрика» и «Стереометрика» представляют собой справочники по прикладной математике. Среди содержащихся в «Метрике» сведений: формулы для площадей правильных многоугольников, формула Герона для расчёта площади треугольника по длинам его сторон, правила численного решения квадратных уравнений, алгоритмы извлечения квадратных и кубических корней. В основном изложение в математических трудах Герона догматично – правила часто не выводятся, а только показываются на примерах. Герон вывел формулу для решения квадратного уравнения a•x2 + b•x = c умножением всех членов на а и прибавлением к обеим половинам уравнения выражения

Древнегреческие математики могли решать некоторые виды квадратных уравнений, сводя их решение к геометрическим построениям. Приемы решения уравнений без обращения к геометрии дает Диофант Александрийский (III в.). В дошедших до нас шести из 13 книг «Арифметика» содержатся задачи с решениями.

Способ решение полных квадратных уравнений Диофант изложил в книгах «Арифметика», которые не сохранились. Его трактат «Арифметика» содержит ряд задач, решаемых при помощи квадратных уравнений. В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней. В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам», написанным индийским астрономом и математиком Ариабхатой в 499 году нашей эры. Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому учёному Брахмагупте (около 598 г.). Брахмагупта изложил универсальное правило решения квадратного уравнения, приведённого к каноническому виду: a•x 2 + b•x = c; притом предполагалось, что в нём все коэффициенты, кроме a, могут быть отрицательными. Сформулированное учёным правило по своему существу совпадает с современным.

Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи(он же Леонардо из Пизы или Леонардо Пизанский 1180-1240). Этот объемистый труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники 16-17 вв. и частично 18.

В XVI веке французский юрист, тайный советник короля Франции и математик Франсуа Виет (1540-1603) впервые вводит в обращение буквенные обозначения не только для неизвестных величин, но и для данных, то есть коэффициентов уравнения. Франсуа Виет – замечательный французский математик, положивший начало алгебре как науке о преобразовании выражений, о решении уравнений в общем виде, создатель буквенного исчисления. Виет первым стал обозначать буквами не только неизвестные, но и данные величины. Тем самым ему удалось внедрить в науку великую мысль о возможности выполнять алгебраические преобразования над символами, т.е. ввести понятие математической формулы. Этим он внес решающий вклад в создание буквенной алгебры, чем завершил развитие математики эпохи Возрождения и подготовил почву для появления результатов Ферма, Декарта, Ньютона.

Общее правило решения квадратных уравнений, было сформулировано немецким математиком М. Штифелем (1487-1567). Выводом формулы решения квадратных уравнений общего вида занимался Виет. Формулы, выражающие зависимость корней уравнения от его коэффициентов, были выделены Виетом в 1591 г. Однако свое утверждение он высказывал лишь для положительных корней (отрицательных чисел он не признавал). После трудов нидерландского математика А. Жирара (1595-1632), а также Декарта и Ньютона способ решения квадратных уравнений принял современный вид.

В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Перечислим десять способов решения квадратных уравнений:

• Метод выделения полного квадрата.
• Решение квадратных уравнений по формулам.
• Теорема Виета.
• Свойства коэффициентов.
• Разложение левой части на множители.
• Способ «переброски».
• Графический способ.
• Метод номограммы.
• Геометрические способы. Решение квадратных уравнений с помощью циркуля и линейки.
• Тригонометрический способ.

Решение квадратных уравнений по формуле корней

Квадратное уравнение – алгебраическое уравнение общего вида

где х — свободная переменная, a, b, c — коэффициенты, причём a ≠ 0.

Выражение a•x2 + b•x + c называют квадратным трёхчленом.

Корень — это значение переменной x, обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное равенство.

Элементы квадратного уравнения имеют собственные названия:

• называют первым или старшим коэффициентом,
• называют вторым, средним или коэффициентом при ,
• называют свободным членом.

Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент:

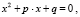
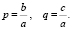
Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.

Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.

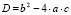
Квадратное уравнение с вещественными коэффициентами a, b cимеет ровно два комплексных корня, о чём гласит основная теорема алгебры. При этом, в зависимости от значения дискриминанта , как один, так и оба корня могут не иметь мнимой части и быть вещественными:

• при D > 0 вещественных корней два, и они вычисляются по формуле

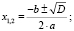
• при D = 0 корень один (о чём так же можно говорить как о двух равных или совпадающих корнях), кратности 2:

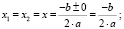
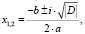
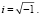
где

Приведем алгоритм решения квадратного уравнения по формуле корней.

Алгоритм – четкое описание последовательности действий, которые необходимо выполнить при решении задачи. Можно сказать, что алгоритм описывает процесс преобразования исходных данных в результаты, т.к. для решения любой задачи необходимо:

1. Ввести исходные данные.

2. Преобразовать исходные данные в результаты (выходные данные).

3. Вывести результаты.

• на естественном языке;
• в виде блок-схемы;
• в виде R-схемы.

Рассмотрим пример алгоритма на естественном языке:

1. Ввести в компьютер числовые значения переменных а, b и с.

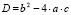
2. Вычислить дискриминант по формуле .

3. Если D > 0, то вычислить и напечатать значения x1 и x2 и перейти к п. 6. Иначе перейти к п. 4.

4. Если D = 0, то вычислить и напечатать значение x1 = x2 = x и перейти к п. 6. Иначе перейти к п. 5.

5. Вычислить действительную и мнимую части комплексных корней и напечатать значения пары комплексно сопряженных корней.

6. Прекратить вычисления.

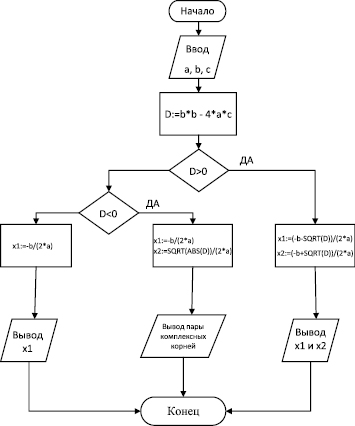
Представим разработанный выше алгоритм в виде блок-схемы.

Блок-схемой называется наглядное графическое изображение алгоритма, когда отдельные его этапы изображаются при помощи различных геометрических фигур – блоков, а связи между этапами (последовательность выполнения этапов) указываются при помощи стрелок, соединяющих эти фигуры. Блоки сопровождаются надписями. Типичные действия алгоритма изображаются геометрическими фигурами согласно ГОСТ 19.701-90.

Интегрированная среда программирования Паскаль-ABC. Разработка и тестирование программы

Наиболее распространенным в настоящее время языком программирования для компьютеров серии IBM PC является Паскаль. Это язык высокого уровня, отличающийся простотой синтаксиса, структурированный и удобный для начального обучения программированию.

Учебная система программирования Паскаль-ABC представляет собой диалект стандартного языка Паскаль. Система создавалась на факультете математики, механики и компьютерных наук ЮФУ как учебная среда программирования (автор — кандидат физико-математических наук, доцент кафедры алгебры и дискретной математики С.С. Михалкович).

Система Паскаль-ABC предназначена для обучения программированию на языке Паскаль и ориентирована на школьников и студентов младших курсов. По мнению разработчиков этой системы, первоначальное обучение программированию должно проходить в достаточно простых и дружественных средах, в то же время эти среды должны быть близки к стандартным и иметь богатые и современные библиотеки подпрограмм.

Система программирования Паскаль-ABC представляет собой единство компилятора языка программирования Паскаль и инструментальной программной оболочки, называемой средой. Среда предоставляет необходимые сервисные услуги и способствует повышению эффективности процессов разработки, отладки и испытаний программ, что облегчает труд программиста.

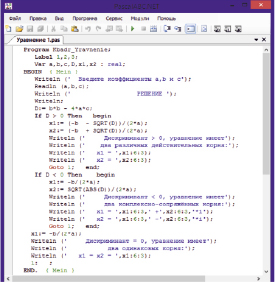
Рис. 2. Скриншот разработанной программы решения квадратных уравнений в среде Паскаль-ABC

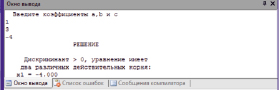
Рис. 3. Скриншот результата вычислений действительных различных корней

На рис. 2 представлен скриншот разработанной программы решения квадратных уравнений в среде Паскаль-ABC. Т.к. программа имеет три разветвления, то протестируем каждую из ветвей.

Решим квадратное уравнение, имеющее два действительных корня (D > 0):

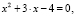
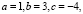
Здесь поэтому формула корней квадратного уравнения имеет вид:

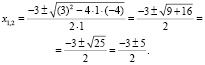
Тогда, вычисленные корни имеют вид:

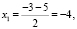
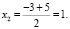
Скриншот полученного результата представлен на рис. 3.

Решим квадратное уравнение, имеющее один действительный корень (D = 0):

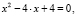
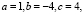
Здесь поэтому формула корней квадратного уравнения имеет вид:

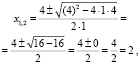
Скриншот полученного результата представлен на рис. 4.

Решим квадратное уравнение, имеющее пару комплексно сопряженных корней (D < 0):

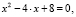
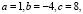
Здесь поэтому формула корней квадратного уравнения имеет вид:

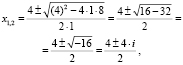
т.е: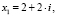

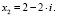
Скриншот полученного результата представлен на рис. 5.

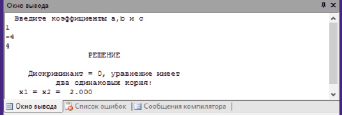
Рис. 4. Скриншот результата вычислений двух равных корней

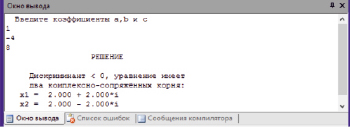
Рис. 5. Скриншот результата вычислений двух комплексно сопряженных корней

В результате выполнения моей научно-исследовательской работы достигнута цель исследования – разработана программа нахождения корней уравнения второй степени в среде программирования Паскаль-ABC. Программа протестирована по всем трем ветвям вычислительного процесса: решения квадратного уравнения в случае двух действительных различных корней, случая двух действительных равных (кратных) корня и при наличии двух комплексно сопряженных корней.

При этом я ознакомился с историей квадратных уравнений и различными методами их решения. Освоил некоторые приемы программирования в интегрированной среде Паскаль-ABC. Разработал алгоритм и блок-схему нахождения корней квадратного уравнения. Надеюсь, что полученные знания и навыки помогут мне успешно сдать ОГЭ по дисциплинам математика и информатика и ИТК.

Источник: school-herald.ru

Как написать программу квадратного уравнения

Обратим внимание, что для данной программы коэффициент a не должен быть равен нулю. Иначе в первой ветке условного оператора будет происходить попытка деления на 0.

Если a = 0 , то квадратное уравнение превращается в линейное, которое решается иным способом. Оно всегда имеет один корень.

Решение квадратного уравнения

Уравнение вида a⋅x 2 + b⋅x + c = 0 — квадратное уравнение.

a, b, c — действительные числа, a ≠ 0.

Для того чтобы вычислить корни квадратного уравнения, нужно сначала найти дискриминант.

• если D 0, то уравнение имеет два действительных корня:

• x1 = (-b + √D) / (2⋅a);
• x2 = (-b + √D) / (2⋅a).

Программа для решения квадратного уравнения на языке программирования Паскаль

Функция sqr языка Pascal используется для возведения числа в квадрат.
Функция sqrt используется для получения квадратного корня числа.
В программе используется форматированный вывод вещественных чисел. variable:8:3 — означает, что для вывода переменной предусмотрено 8 символов, 5 из них под целую часть и 3 под дробную.

Программа для решения квадратных уравнений на C++

Довольно часто в пособиях по программированию встречаются задания по нахождению решений каких-нибудь математических уравнений. Задача нахождения корней квадратного уравнения — это довольно тривиальная задача, как и многие другие задачи. Решается она очень просто при помощи листа бумаги и ручки, но решение можно автоматизировать посредством написания прикладной программы и её использования. В этой статье мы напишем такую программу.

Алгоритм решения квадратного уравнения

Многие знают, что уравнение вида ax 2 + bx + c = 0 , где a не равно 0, называют квадратным уравнением.

Существуют различные способы решения квадратных уравнений, но мы рассмотрим решение через дискриминант.

Обозначается дискриминант буквой D . Из школьного курса знаем, что D = b 2 — 4ac .

Существует несколько условий:

• Если D > 0, то решение имеет 2 различных вещественных корня.
• Если D = 0, то оба вещественных корня равны.
• Если D для вводавывода в консоли, #include для работы с математическими функциями и область using namespace std;

Для вас это может быть интересно:

Программа для решения квадратных уравнений на C++ : 24 комментария

1. Nicknixer Автор записи 15.10.2016

Не так сложно, как Вам кажется! Немного литературы, немного практики и смотреть на код решения такой задачи Вы будете по-другому.

Доброго времени суток! Помогите пожалуйста написать программу, которая считает сколько символов в ряде двумерного массива. То есть , например массив 5 на 5, сколько символов в 1 ряде, сколько во 2 и т.д.

Ответил вам по электронной почте

Критику принимаете?
Программа дырявая как сито.

Если число очень маленькое, но положительное, например 10^(-20) — у вас будет переполнение или типо того. Оператор > проверяет знак числа (это отдельный бит), а оператор == для дробных чисел не имеет смысла, т.к. в младших разрядах числа обычно находится какой-нибудь мусор, который при таком сравнении дает false.

x = ( -1*b + sqrt(b*b — 4*a*c) ) / (2 * a);
x = ( -1*b — sqrt(b*b — 4*a*c) ) / (2 * a);

Тут есть три вопроса:
1) зачем два раза вычислять одно и тоже (я про корень)
2) что делать если мне корни надо как-то использовать, а не просто вывести (тут есть проблема, ведь у меня то один корень — то два). Чтобы лучше понять в чем проблема — попробуйте вынести вычисление корней в отдельную функцию. У вас то вообще, если корень один — то их выведется все равно два, одинаковых.
3) в переменной «a» может быть ноль (или близкое к нулю число) — при этом мы получим деление на ноль (а точнее, переполнение).

Но это ведь еще не все. Что будет если и «a» и «b» равны нулю? — тебе надо рассмотреть два варианта — если c = 0 (условно, близко к нулю), то корней бесконечно много. А если c != 0, то корней нет.

Вообще, эта задача — прекрасный пример для юнит-тестирования и демонстрации принципов разработки через тестирование. Именно его я рассматривал в своей статье по теме тестирования: Юнит-тестирование. Пример. Boost Unit Test.

Дело в том, что тут куча вариантов сделать ошибку, при этом их понимание приходит не сразу, т.е. школьник решая задачу напишет по формуле которой учили (ну и вот как у вас). А потом надо разбираться и смотреть как программа может сломаться, при этом разрабатывать тесты.

1. Николай Сергейчук Автор записи 09.02.2017

Принимаем
Согласен с вами во всём! Программу можно реализовать намного лучше, используя различные проверки и валидацию входных данных.
Однако, статья рассчитана на аудиторию, которая только начинает познавать программирование или делает лабораторную. Чтобы людям легче было понять, реализация данной программы упрощена до невозможности. И, возможно, несправедливо было с моей стороны не предупредить их о возможных ошибках в работе программы, которые могут вскрыться позже, если подать на вход определенные значения.
Кстати, у вас интересная статья по тестированию!

Николай, доброго времени суток! Можете помочь с написанием програмки в с++? 1-1/2!+1/3!-1/4!+1/5! и так до 1/100! ? Чтобы при заднии в строке номера члена последовательности выдавал сумму до него по такой вот формуле? Буду очень благодарен!

Пожалуйста подскажите как ввести экран правильный ответ дискриминанта

Помогите решить в Dev C++
Sqrt x^2+1+sqrt|x|,x0

Здравствуйте, можете помочь с решением биквадратного и триквадратного уравнения?

#include
using namespace std;
int main()
b;
cout <> c;
D = pow(b, 2) — 4 * a * c;
cout

ну и? если даже тупо скопировать код и вставить его в cpp.sh , ничего не работает. поебота какая то этот с++

Уважаемая, Лена! Я, надеюсь, вы знаете, что код программы, написанной на языке программирования C++ нельзя тупо вставить в блокнот и сохранить под названием «cpp.sh»? Если не знали, то я, видимо, открыл для вас Америку!

помогите решить. заданы 3 перемены a.b.c записать вы радение на С
b,
b и а не равно != с

iconcerts где забыл
#include

Я ради интереса написал программу нахождения корней квадратного уравнения на С++, с выводом корней как в десятичном виде, так и в виде простой дроби (причём уже сокращённой), потому что выводя корни в десятичном виде программа их одновременно сокращает и округляет и 1/3 превращается в 0.333333 хотя на самом деле 0.333333 (3), то есть для проверки правильно ли нашёл корни ваш ребёнок, вы с получите что-то типа: X1= 0.285714; X2=0.214286, а на самом деле это будет X1=2/7; X2=3/14, кроме того, если корень из дискриминанта не получается целым числом, вы уже получите двойную неточность: сначала при извлечении корня программа отсечёт значение до 4-6 цифр после запятой с округлением, а затем сделает то же самое при делении числителя на знаменатель. Я и здесь сделал вывод корней в двух значениях: в десятичном и в виде выражения X1= (-b + sqrt(D))/(2*a); X2= (-b — sqrt(D))/(2*a), то есть выводится примерно вот так X1=-5+sqrt(21)/2; X2=-5-sqrt(21)/2 с одновременным разложением дискриминанта под корнем на множители, вынесением этих множителей из-под корня, если они выносятся нацело, их перемножением и дальнейшим сокращением. Вот, например, имеем a=3, b=15, c=3, при решении получаем D=189 программа выдаёт десятичные корни X1= -0.208712 и X2= -4.79129, а в виде выражения имеем: X1= -5+sqrt(21)/2, то есть первоначально получаем: X1= -15+sqrt(189)/6, -> 189=21*9 -> -15+3sqrt(21)/6 далее идёт сокращение на 3 и итог -5+sqrt(21)/2

День добрый.
Недавно начал изучать C++. Решил попробовать написать решение квадратного уравнения именно через оператор вида «условие ? выполняется : не выполняется». Т.е. если условие выполняется, то имеем два решения (даже если d = 0, то тоже должно быть два решения x1 = x2), если d a;
std::cout <> b;
std::cout <> c;
d = pow(b, 2) — 4 * a*c;
d >= 0 ? xfst = ((-b + sqrt(d)) / double(2 * a)) , xscd = ((-b — sqrt(d)) / double(2 * a)) : std::cout

1. Николай Сергейчук Автор записи 12.02.2020

if (d >= 0) = 0 ) = 0) = 0, y2 >= 0)

Свежие записи

• Сера — химические свойства, получение, соединения.
• Нитрат кальция: способы получения и химические свойства
• Кальций: способы получения и химические свойства
• Гидроксид натрия: способы получения и химические свойства
• Гидроксид кальция: способы получения и химические свойства

Источник: al-shell.ru

Программа решения квадратных уравнений

В данной работе содержится технический проект к программе составленной в среде Lazarus.

Скачать:

ВложениеРазмер

kvadratnye_uravneniya.rar	364.6 КБ

Предварительный просмотр:

ГОУ СПО «ЗУБОВО-ПОЛЯНСКИЙ ПЕДАГОГИЧЕСКИЙ КОЛЛЕДЖ»

___________ Ласкин В.О.

«___» ______________ 2011 г.

ПРОГРАММА РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ

Исполнитель, ______________ Пинясов В.

Зубова Поляна, 2011 г.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К ТЕХНИЧЕСКОМУ ПРОЕКТУ ………….3

Структура входных и выходных данных …………………………………3

Алгоритм решения задачи ………………………………………………..3

Листинг программного кода ………………………………………………7

Конфигурация технических средств ……………………………………14

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ …………………………15

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К ТЕХНИЧЕСКОМУ ПРОЕКТУ

1. Общие положения