Сегодня мы поговорим про то, как построить математический график при помощи языка Python за 10 минут. Мы рассмотрим построение параметрических кривых в трехмерном и двумерном пространстве с использованием различных примеров.
У многих из нас со школьной скамьи остались не самые приятные воспоминания о математике. Кто-то воспринимал её как необходимое зло: сложное и скучное, но обязательное. Кто-то же отказывался понимать математику от слова совсем.
Так или иначе, но наше школьное образование было ориентировано скорее на запоминание и заучивание, а не на размышления. По большому счету не было никакой мотивации разбираться в основах математики или в том, как она на самом деле работает. Идея заключалась в том, чтобы просто узнать, какие задачи решает определенная формула, запомнить правильный набор шагов и воспроизвести все это на экзамене.
Однако математика намного обширнее и интереснее того, что мы учили в школе. Если взять, например, кинематику, можно увидеть настоящую магию математики. Кинематика известна как «геометрия движения» – это изучение взаимодействия между движущимися телами во времени. Хотя бы раз увидите такое визуальное представление математических функций — и они оживут для вас. Возможно, в тот момент вы почувствуете, что впервые понимаете их правильно.
Рисуем ГРАФИКИ и пишем КОД — Маленький проект
Итак, давайте научимся самостоятельно моделировать данные и начнем писать собственные скрипты. Сегодня мы поговорим о параметрических кривых и как их строить, используя Python и такие библиотеки, как NumPy, SymPy и Matplotlib.
Построение параметрических кривых
Параметрические кривые поистине завораживают! Если говорить простым языком, параметрическую кривую можно понимать как след, оставляемый движением частицы в пространстве. Говоря более формально, этот след моделируется функцией, определяемой от интервала I до различных точек в пространстве E .
Для трехмерного случая, если x , y и z заданы как функции переменной t в I (это параметр), мы получаем уравнения x = f(t) , y = g(t) и z = h(t) . Оценивая каждое значение параметра t в каждом из этих уравнений, мы получаем точку p(t) = (x(t),y(t),z(t)) в пространстве. Проделав эту процедуру для значений t , меняющихся в интервале I , мы получим параметрическую кривую.
Проведя небольшое исследование, попробовав несколько моделей вручную и потратив много часов на работу над сценарием, мы нашли решение. Оно выглядит следующим образом:
import sympy as sp import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D t = sp.Symbol(‘t’) function_x = sp.sympify(‘sin(t)’) function_y = sp.sympify(‘cos(t)’) function_z = sp.sympify(‘t**2′) interval = np.arange(0, 100, 0.1) x_values = [function_x.subs(t, value) for value in interval] y_values = [function_y.subs(t, value) for value in interval] z_values = [function_z.subs(t, value) for value in interval] fig = plt.figure(figsize=(10, 10)) ax = plt.axes(projection=’3d’) ax.plot(x_values, y_values, z_values) plt.show()
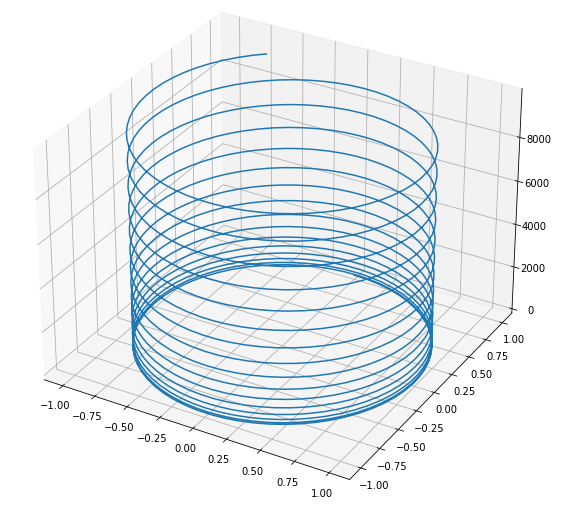
Приведенный выше скрипт позволяет нам генерировать графики для параметрических кривых. К примеру, вот так выглядит график параметрической спирали p(t) = (sin(t),cos(t),sqrt(t3)) , для интервала от 0 до 100.
Graph построение графиков
Как работает скрипт
Скрипт, который мы привели выше, использует такие библиотеки, как SymPy, NumPy и Matplotlib. Давайте разберемся со всем по порядку.
SymPy — это библиотека Python для символьной математики. Она стремится стать полнофункциональной системой компьютерной алгебры (CAS). При этом сохраняется максимально простой код (а значит, понятный и масштабируемый). Библиотека SymPy, кстати, полностью написана на Python.
NumPy — это основной пакет для научных вычислений в Python. Эта библиотека предоставляет:
- объекты многомерного массива,
- различные производные объекты (такие как маскированные массивы и матрицы)
- набор подпрограмм для быстрых операций с массивами, включая математические и логические, манипуляции с фигурами, сортировку, выборку, ввод-вывод, дискретные преобразования Фурье, основные операции линейной алгебры, основные статистические операции и случайное моделирование.
И последняя библиотека из нашего списка — Matplotlib. Это обширная библиотека для создания статических, анимированных и интерактивных визуализаций на Python.
Подготовка
Чтобы использовать перечисленные выше библиотеки в нашем скрипте, мы должны сначала установить их на свой компьютер, выполнив следующую инструкцию в терминале:
pip install numpy sympy matplotlib
Теперь, когда библиотеки установлены, мы можем импортировать их в нашу программу:
import sympy as sp import numpy as np import matplotlib.pyplot as plt
Построение графика трехмерной параметрической кривой
Символьные вычисления в SymPy выполняются с помощью символов. Переменные SymPy являются объектами класса Symbols . Выражение t = sp.Symbol(‘t’) присваивает символ t переменной t , с которой мы теперь можем работать как с математической переменной.
Выглядит это следующим образом:
t = sp.Symbol(‘t’) print(t ** 2) >>> t ^ 2
В рамках этой задачи нам нужно работать с составными выражениями, хранящимися в строке. Поэтому нам нужно сделать преобразование строки в математическое выражение понятным для SymPy. Для этого мы используем функцию sympify.sp.sympify(expression) , которая преобразует параметрическое выражение в общее математическое выражение.
К примеру, наш код будет выглядеть так:
function_z = sp.sympify(‘t^2’) print(function_z + 2) >>> t ^ 2 + 2
Теперь переменная function_z содержит математическое выражение t 2 +2 .
Следующим шагом является возможность оценить параметр t внутри математического выражения. Функция subs() в SymPy позволит нам оценить выражение с заданным значением. Мы можем использовать его следующим образом: expression.subs(t, value) .
Наш код будет выглядеть следующим образом:
value = function_z.subs(t, 5) print(value) >>> 5 ^ 2 = 25
Поскольку мы говорим о параметрических функциях, нас интересует оценка функции на последовательности вещественных значений в пределах интервала. Для этого мы используем функцию arange() в NumPy.
Функция np.arange(start, stop, step) создает массив NumPy со значениями в интервале (start,stop) с приращением шага, то есть мы идем от start до stop-1 с определенным шагом step .
Наш код будет выглядеть так:
interval = np.arange(0, 10, 1) print(interval) >>> array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
После создания массива интервалов нам нужно перебрать значения t и оценить каждое значение внутри функции. Для этого мы будем использовать генератор списков в Python и функцию subs() библиотеки SimPy.
О генераторах списков можно почитать в статье «Генераторы списков в Python для начинающих».
Функция subs() получает символ t (который мы сохранили в переменной t ) и значение каждого из элемента в качестве параметров.
Выглядит это примерно следующим образом:
z_values = [function_z.subs(t, value) for value in interval] print(z_values) >>> [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
График функции на C++ в GUI с анимацией
Предположим, что у вас вот такое задние: создать GUI C++ VS приложение графики и анимации. Например, конкретно, такое:
- Обеспечивает возможность задания параметра p в каноническом уравнении параболы в прямоугольной системе координат (y 2 = 2px, p>0).
- Выводит кривую на экран.
- Анимирует построение параболы.
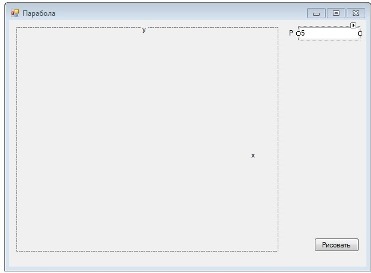
Рисовать будем по точкам, используя два массива с их координатами.
int m_x[200]; int m_y[200];
После нажатия кнопки «Рисовать!» инициализируем (очищаем) эти массивы координат в цикле:
for (int i1=0; i1
Получаем параметр p
double p = Convert::ToDouble(textBox1->Text);
Заполняем массив координат по формуле:
for (i=0; iRefresh(); >
Рисуем параболу по точкам
for (int j=0; jGraphics->FillRectangle(System::Drawing::Pens::Red->Brush, m_x[j]+200, m_y[j]+200, 1, 1);//одно значение y e->Graphics->FillRectangle(System::Drawing::Pens::Red->Brush, m_x[j]+200, 0-m_y[j]+200, 1, 1);// второе значение y >
Точнее, рисуем не по точкам, а по закрашенным прямоугольникам. Здесь два значения y – следуя каноническому уравнению параболы. Результат:
Стоит отметить, что в программе еще нобходимо реализовать так называемую «защиту от дураков» (ввод букв вместо цифр, к примеру), а также обеспечить проверку на >0. Еще необходимо немного изменить анимацию: более правильно будет делать её или в отдельном потоке, или через таймер. Зачем?
Дело в том, что когда у нас идет прорисовка графика функции, все приложение зависает и не откликается. Правда, анимация параболы идет не более двух секунд, но все равно это не совсем правильно. Расчеты и прорисовка реализуются в разных методах и потоках (backgroundWorker).
Это был пример создания GUI C++ VS приложение графики и анимации. На самом деле их немало, есть, к примеру, и такие:
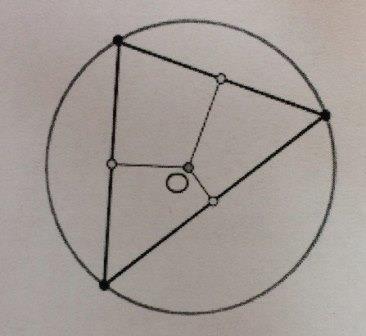
- Обеспечивает возможность задания длин сторон треугольника (с проверкой возможности построения).
- Выводит треугольник на экран.
- Анимирует построение описанной окружности (рассмотреть остроугольный, тупоугольный и прямоугольный треугольник).

Автор этого материала — я — Пахолков Юрий. Я оказываю услуги по написанию программ на языках Java, C++, C# (а также консультирую по ним) и созданию сайтов. Работаю с сайтами на CMS OpenCart, WordPress, ModX и самописными. Кроме этого, работаю напрямую с JavaScript, PHP, CSS, HTML — то есть могу доработать ваш сайт или помочь с веб-программированием. Пишите сюда.
статьи IT, си плюс плюс, графики, функции, gui
Бесплатный https и
домен RU в подарок
Источник: upread.ru
Программа на си для построения графика функции
В этой статье мы разберем программу на языке программирования си для построения графиков функций. В нашей программе будут отражаться система координат с делениями и подписями на них и будут строиться графики двух функций, который может сам задать пользователь.
В программе на си для построения графика функции вводятся следующие константы
X0 , Y0 — координаты центра координат
k – масштаб одного деления на осях (сколько пикселов в одном делении)
Опишем все функции и процедуры используемые в программе для построения графиков функций
Подробно о задании функций и процедур в си
int osx (float x) переводит реальную координату на оси ox в координату экрана
int osy (float y) переводит реальную координату на оси oy в координату экрана
float F1 ( float x ) и float F2 ( float x ) задают функции , графики которых мы будем строить
void Point ( float x, float y, int color ) рисует точку графика функции на экране
Перед построением графиков функций необходимо построить систему координат. Для построения системы координат используется процедура
void Axes()
В этой процедуре в цикле for рисуются линии меток делений на равном расстоянии друг от друга, который определяется масштабом одного деления k и выводятся значения делений с помощью двух операторов
sprintf ( s, «%d», i ); // записываем в строковую переменную число деления
outtextxy ( xe-10, Y0+4, s ); // вывод числа
Процедура grafik1() и grafik2() строят графики функций f1 и f2
В этих процедурах в цикле for для всех доступных значений x определяется координата y и точка графика строится с помощью процедуры point()
Пример работы программы построения графиков на си, функции пользователь может менять

Программа на си для построения графиков функций
#include
#include //графический режим
#include // математические функции
//————————————————
const int X0 = 100, Y0 = 400;// координаты центра координат
const float k = 15;// масштаб в точках одного деления на графике
//——————————————
// перевод y в координаты экрана
//——————————————
int osx (float x)
return X0+k*x;
>
//——————————————
//перевод y в координаты экрана
//——————————————
int osy (float y)
return Y0-k*y;
>
// первая функция
float F1 ( float x )
return sqrt(2*x);
>
// вторая функция
float F2 ( float x )
return x*x/2;
>
// построение осей
void Axes()
int i, xe,ye,y1;
char s[10];
line ( X0, 0, X0, 599 ); // ось ox
line ( 0, Y0, 799, Y0 ); // ось oy
// метки на оси ox
for ( i = 1; i xe = osx ( i );
line ( xe, Y0-2, xe, Y0+2 ); // рисуем деление разметки
sprintf ( s, «%d», i ); // записываем в строковую переменную число деления
outtextxy ( xe-10, Y0+4, s ); // вывод числа
>
// метки на оси oy
for ( i = 1; i ye = osy( i+1 );
line ( X0-2, ye, X0+2, ye ); // рисуем деление
sprintf ( s, «%d»,i ); // записываем в строковую переменную число деления
outtextxy ( X0+10, ye+4, s ); // вывод числа
>
>
// построение точки графика функции
void Point ( float x, float y, int color )
int xe, ye;
xe = osx(x);
ye = osy(y);
if ( xe >= 0 xe < 800 ye >= 0 ye < 600 )
putpixel(xe, ye, color);
>
// построение графика первой функции
void grafik1()
float x, h, xmin, xmax;
h = 1 / k;
xmin = (-X0)/ k;
xmax=(800-X0)/k;
for ( x = xmin; x Point(x, F1(x), WHITE);
>
>
// построение графика второй функции
void grafik2()
float x, h, xmin, xmax;
h = 1 / k;
xmin = (-X0)/ k;
xmax=(800-X0)/k;
for ( x = xmin; x Point(x, F2(x), WHITE);
>
>
// главная программа
main ()
initwindow ( 800, 600 ); // создать окно для графики
Axes(); // построение и разметка осей координат
grafik1(); // строим график первой функции
grafik2(); // строим график второй функции
getch(); // ждать нажатия на клавишу
closegraph(); // закрыть окно для графики
>
Полезно почитать по теме построение графиков функций в программа си
Графика в си
Процедуры и функции в си
Комментарии ( 0 )
Нет комментариев. Ваш будет первым!
Источник: itrobo.ru