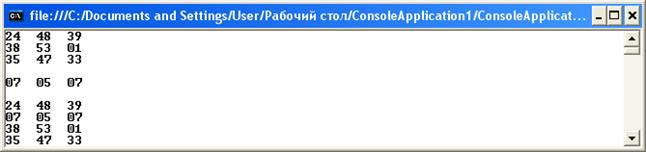
Задача: разработать на C++ программу, выполняющую умножение двух матриц. Из курса высшей математики известно, что произведение двух матриц имеет смысл только тогда, когда число столбцов матрицы А совпадает с числом строк матрицы В.
Поэтому в приведённом ниже фрагменте кода задаём ввод пользователем одной и той же переменной — n числа столбцов матрицы А и числа строк матрицы В. Затем вводятся число строк матрицы А и число столбцов матрицы В.
Код C++
cout «Enter cols count in matrix A and rows count in matrix B: » ;
cout «Enter rows count in matrix A: » ;
cout «Enter cols count in matrix B: » ;
Далее выделяем память под два динамических двумерных массива — соответственно матрицы А и В. Организуем ввод пользователем элементов этих двух матриц и вывод на экран заполненных матриц.
Код C++
int **aArr = new int *[m];
for (i = 0; i new int [n];
for (i = 0; i for (j = 0; j «Enter arrays elements of matrix A » ;
Двумерные массивы вывод. Заполнение. Двумерный массив циклы. C++ для начинающих. #32
cout «Matrix A: » for (i = 0; i for (j = 0; j int **bArr = new int *[n];
for (i = 0; i new int [q];
for (i=0; i for (j = 0; j «Enter arrays elements of matrix B » ;
cout «Matrix B: » for (i = 0; i for (j = 0; j Код C++
int **cArr = new int *[i];
for (i = 0; i new int [j];
Затем — цикл вычисления произведения двух матриц по формуле . В цикле происходит суммирование всех произведений элементов, предусмотренной формулой.
Код C++
int **cArr = new int *[i];
for (i = 0; i new int [j];
for (i = 0; i for (j = 0; j for ( int k = 0; k Код C++
cout «Matrix C: » for (i = 0; i for (j = 0; j Код C++
using namespace std;
cout «Enter cols count in matrix A and rows count in matrix B: » ;
cout «Enter rows count in matrix A: » ;
cout «Enter cols count in matrix B: » ;
int **aArr = new int *[m];
for (i = 0; i new int [n];
for (i = 0; i for (j = 0; j «Enter arrays elements of matrix A » ;
cout «Matrix A: » for (i = 0; i for (j = 0; j int **bArr = new int *[n];
for (i = 0; i new int [q];
for (i=0; i for (j = 0; j «Enter arrays elements of matrix B » ;
cout «Matrix B: » for (i = 0; i for (j = 0; j int **cArr = new int *[i];
for (i = 0; i new int [j];
for (i = 0; i for (j = 0; j for ( int k = 0; k «Matrix C: » for (i = 0; i for (j = 0; j return 0;
Источник: function-x.ru
Примеры алгоритмов обработки матрицами
Матрица — это двумерный массив, каждый элемент которого имеет два индекса: номер строки — i; номер столбца — j. Поэтому для работы с элементами матрицы необходимо использовать два цикла. Если значениями параметра первого цикла будут номера строк матрицы, то значениями параметра второго — столбцы (или наоборот). Обработка матрицы заключается в том, что вначале поочередно рассматриваются элементы первой строки (столбца), затем второй и т.д. до последней. Рассмотрим основные операции, выполняемые над матрицами при решении задач.
Алгоритмы матрицы, чужой голос в голове, циклы программ. Mark Attention
Алгоритм ввода-вывода матриц
Матрицы, как и массивы, нужно вводить (выводить) поэлементно. Блок-схема ввода элементов матрицы изображена на рис. 4.1. Вывод матрицы организуется аналогично вводу.
| Рис. 4.1. Ввод элементов матрицы | Рис. 4.2. Свойства элементов матрицы |
Рассмотрим несколько задач обработки матриц. Для их решения напомним читателю некоторые свойства матриц (рис. 4.2):
- если номер строки элемента совпадает с номером столбца (i = j), это означает что элемент лежит на главной диагонали матрицы;
- если номер строки превышает номер столбца (i > j), то элемент находится ниже главной диагонали;
- если номер столбца больше номера строки (i, то элемент находится выше главной диагонали.
- элемент лежит на побочной диагонали, если его индексы удовлетворяют равенству i+j-1 = n;
- неравенство i+j-1 < nхарактерно для элемента находящегося выше побочной диагонали;
- соответственно, элементу лежащему ниже побочной диагонали соответствует выражение i+j-1 > n.
Примеры алгоритмов обработки матрицами
ПРИМЕР 4.1. Найти сумму элементов матрицы, лежащих выше главной диагонали (рис 4.3).
Алгоритм решения данной задачи (рис. 4.4) построен следующим образом: обнуляется ячейка для накапливания суммы (переменная S). Затем с помощью двух циклов (первый по строкам, второй по столбцам) просматривается каждый элемент матрицы, но суммирование происходит только в том случае если, этот элемент находится выше главной диагонали, то есть выполняется свойство i < j.
| Рис. 4.4. Блок-схема примера 4.1 (алгоритм 1) | Рис. 4.5. Блок-схема примера 4.1 (алгоритм 2) |
ПРИМЕР 4.2. Вычислить количество положительных элементов квадратной матрицы, расположенных по ее периметру и на диагоналях. Напомним, что в квадратной матрице число строк равно числу столбцов.
Прежде чем преступить к решению задачи рассмотрим рисунок 4.6, на котором изображена схема квадратных матриц различной размерности. Из условия задачи понятно, что не нужно рассматривать все элементы заданной матрицы. Достаточно просмотреть первую и последнюю строки, первый и последний столбцы, а так же диагонали.
Все эти элементы отмечены на схеме, причем черным цветом выделены элементы, обращение к которым может произойти дважды. Например, элемент с номером (1,1) принадлежит как к первой строке, так и к первому столбцу, а элемент с номером (N,N) находится в последней строке и последнем столбце одновременно. Кроме того, если N — число нечетное (на рисунке 4.6 эта матрица расположена слева), то существует элемент с номером (N/2+1, N/2+1), который находится на пересечении главной и побочной диагоналей. При нечетном значении N (матрица справа на рис. 4.6) диагонали не пересекаются.
Итак, разобрав подробно постановку задачи, рассмотрим алгоритм ее решения. Для обращения к элементам главной диагонали вспомним, что номера строк этих элементов всегда равны номерам столбцов. Поэтому, если параметр i изменяется циклически от 1 до N, то Ai,i — элемент главной диагонали. Воспользовавшись свойством, характерным для элементов побочной диагонали получим: i+j-1 = n > j = n-i+1, следовательно, для i =1,2,…, n элемент Аi,n-i+1 — элемент побочной диагонали. Элементы, находящиеся по периметру матрицы записываются следующим образом: А1,i — первая строка, АN,i — последняя строка и соответственно Аi,1 — первый столбец, Аi,N — последний столбец.
Блок-схема описанного алгоритма изображена на рис. 4.7. В блоке 1 организуется цикл для обращения к диагональным элементам матрицы. Причем в блоках 2-3 подсчитывается количество положительных элементов на главной диагонали, а в блоках 5-6 на побочной. Цикл в блоке 6 задает изменение параметра i от 2 до N-1.
Это необходимо для того, чтобы не обращать к элементам, которые уже были рассмотрены: A11, A1N, AN,1 и AN,N. Блоки 7-8 подсчитывают положительные элементы в первой строке, 9 и 10 — в последней строке, 11 и 12 — в первом столбце, а 13 и 14 в последнем. Блок 15 проверяет, не был ли элемент, находящийся на пересечении диагоналей, подсчитан дважды. Напомним, что это могло произойти только в том случае, если N — нечетное число и этот элемент был положительным. Эти условия и проверяются в блоке 16, который уменьшает вычисленное количество положительных элементов на единицу.
ПРИМЕР 4.3. Проверить, является ли заданная квадратная матрица единичной. Единичной называют матрицу, у которой элементы главной диагонали — единицы, а все остальные — нули.
Решать задачу будем так. Предположим, что матрица единичная (FL=ИСТИНА) и попытаемся доказать обратное. Если окажется, что хотя бы один диагональный элемент не равен единице или любой из элементов вне диагонали не равен нулю, то матрица единичной не является (FL=ЛОЖЬ). Воспользовавшись логическими операциями все эти условия можно соединить в одно и составить блок-схему (рис. 4.8).
| Рис. 4.8. Блок-схема к примеру 4.3 |
ПРИМЕР 4.4. Преобразовать исходную матрицу так, чтобы первый элемент каждой строки был заменен средним арифметическим элементов этой строки.
Для решения данной задачи необходимо найти в каждой строке сумму элементов, которую разделить на их количество. Полученный результат записать в первый элемент соответствующей строки. Блок-схема алгоритма решения приведена на рис. 4.9.
ПРИМЕР 4.5. Задана матрица An, m. Сформировать вектор Pm, в который записать номера строк максимальных элементов каждого столбца.
Алгоритм решения этой задачи следующий: для каждого столбца матрицы находим максимальный элемент и его номер, номер максимального элемента j -го столбца матрицы записываем в j -й элемент массива P. Блок-схема алгоритма приведена на рис. 4.10.
| Рис. 4.9. Блок-схема алгоритма примера 4.4 | Рис. 4.10. Блок-схема алгоритма примера 4.5 |
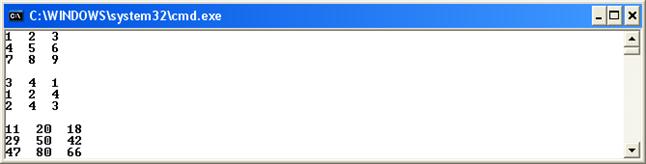
ПРИМЕР 4.6. Написать программу умножения двух матриц An,m и Bm,l.
Например, необходимо перемножить две матрицы
Воспользовавшись правилом «строка на столбец», получим матрицу:
В общем виде формула для нахождения элемента Ci,j матрицы имеет вид:
| где i = 1,Nи j = 1,L. |
Обратите внимание, что проводить операцию умножения можно только в том случае, если количество строк левой матрицы совпадает с количеством столбцов правой. Кроме того, A >< B ≠ B >< A.
Блок-схема, изображенная на рис. 4.11, реализует расчет каждого элемента матрицы C в виде суммы по вышеприведенной формуле.
ПРИМЕР 4.7. Поменять местами n -й и l-й столбцы матрицы A(k,m). Блок-схема приведена на рис. 4.12.
| Рис. 4.11. Алгоритм умножения двух матриц | Рис. 4.12. Блок-схема алгоритма примера 4.7 |
ПРИМЕР 4.8. Преобразовать матрицу A(m,n) таким образом, чтобы каждый столбец был упорядочен по убыванию. Алгоритм решения этой задачи сводится к тому, что уже известный нам по предыдущей главе алгоритм упорядочивания элементов в массиве выполняется для каждого столбца матрицы. Блок-схема приведена на рис. 4.13.
ПРИМЕР 4.9. Преобразовать матрицу A(m,n) так, чтобы строки с нечетными индексами были упорядочены по убыванию, c четными — по возрастанию. Блок-схема приведена на рис. 4.14.
| Рис 4.13. Блок-схема алгоритма примера 4.8 | Рис. 4.14. Блок-схема алгоритма примера 4.9 |
Источник: poisk-ru.ru
Типовые алгоритмы работы с матрицами
1. Просуммировать элементы строк матрицы a. Результат получить в виде вектора (одномерного массива) b.
int[] b = new int[3];

Аналогично осуществляется формирование одномерных массивов из значений максимальных (минимальных) элементов строк, индексов максимальных (минимальных) элементов строк и т.п. (см. соответствующие алгоритмы для одномерных массивов).
Если необходимо осуществить обработку столбцов матрицы, то внешний цикл необходимо организовать по номеру столбца, а внутренний — по номеру строки. В остальном алгоритмы аналогичны.
2. Поменять местами ii-ю и jj-ю строки матрицы.
Поменять местами строки означает поменять местами каждую пару соответствующих элементов этих строк, т.е. необходим цикл по столбцам:
int ii = 1, jj = 2;
p = a[ii, k]; a[ii, k] = a[jj, k]; a[jj, k] = p;

Столбцы меняются местами аналогично (цикл организуется по строкам).
3. Удалить k-ю строку матрицы.
Чтобы удалить строку, необходимо переместить все строки, расположенные после k-й, на одну позицию вверх. Для перемещения строки нужно организовать цикл по элементам строки, т.е. по столбцам:

Удаление столбца осуществляется аналогично (внутренний цикл по элементам столбца, т.е. по строкам).
4. Вставить новую строку, заданную вектором b[m], после k-й строки матрицы.
Вначале нужно освободить место для новой строки, переместив строки, расположенные после k-й, на одну позицию вниз. (При объявлении матрицы предусмотреть необходимость соответствующего увеличения ее размера.)
Перемещение строк нужно начинать с последней строки (см. аналогичный алгоритм для одномерных массивов в п. 3.1):
int[,] a = new int[4, 3];
Random r = new Random();
for (int i = n — 1; i >= k; i—)
Замечание. Здесь переменная r – экземпляр класса Random, который представляет генератор псевдослучайных чисел. Метод Next(maxValue) создает случайное число в диапазоне значений от нуля до числа maxValue, указанного в качестве аргумента метода. r.Next(55) – метод Next, определенный в классе Random и примененный к экземпляру класса r – генерирует следующее псевдослучайное число.
Вставка столбца осуществляется аналогично.
5. Найти сумму элементов матрицы.
Здесь нужно обратиться к каждому элементу матрицы и добавить его к сумме:

Аналогично осуществляется поиск максимального элемента во всей матрице.
Далее будут рассмотрены типовые алгоритмы для квадратной матрицы a размером n*n.
6. Найти сумму элементов, расположенных на главной диагонали (след матрицы).
Элементы, расположенные на главной диагонали, имеют одинаковые индексы (номера строк и столбцов совпадают) и представляют, таким образом, одномерный массив:
Аналогично можно организовывать и другие алгоритмы для работы с диагональными элементами (нахождение максимального элемента и т.п.).
7. Найти сумму элементов, расположенных ниже главной диагонали (включая диагональ), т.е. просуммировать элементы нижнего треугольника матрицы.
Здесь во внешнем цикле (по строкам) номера строк изменяются от 0 до n–1, но в каждой i-й строке суммируются только элементы, расположенные до диагонального элемента этой строки, т.е. до i-го:
8. Транспонирование матрицы с получением результата в том же массиве. Для квадратной матрицы размером n´ n требуется переставлять элементы, расположенные симметрично относительно главной диагонали.
for (int j = i + 1; j < n; j++)
p = a[i, j]; a[i, j] = a[j, i]; a[j, i] = p;

Для прямоугольной матрицы размером n´ m транспонированная матрица может быть получена на месте исходной, если последняя размещена в массиве размером не менее чем n´n (предполагается, что n > m). При этом можно использовать приведенный выше алгоритм. Фиктивные столбцы, дополняющие исходную матрицу до квадратной, помещаются в этом случае в фиктивные строки транспонированной матрицы.
9. Умножение матрицы на вектор.
Требуется умножить матрицу а размером n´m на вектор b размером m. Для этого необходимо вычислить
c [ i ] = а [ i, j ] b [ j ], i = 0. n – 1.
int[] c = new int[3];
10. Умножение матрицы на матрицу. Требуется умножить матрицу а размером n´ k на матрицу b размером k´m. Для этого необходимо вычислить
int[,] c = new int[3, 3];
int n = 3, m = 3, k = 3;
s = s + a[i, l] * b[l, j];
11. Определение номера k (нумерация начинается с 0) элемента a[i, j] матрицы размера n´m (нумерация n и m начинается с 1), заданной в виде одномерного массива по строкам:
k =(i -1) m + j- 1;
12. Определение номера k (нумерация начинается с 0) элемента a[i, j] симметрической матрицы размером n´n (нумерация n – с 1), заданной своим верхним треугольником в одномерном массиве b размером (n+ 1) n /2:
k = (2 n – (i– 1) +1)(i – 1)/2 + j – (i – 1) – 1, i = 1, 2. n; j = i, i +1. n.
Элементы нижнего треугольника определяются как
a [ i, j ] = a [ j, i ], i = 2. n; j = 1. i – 1.
Пример 3.5. В одномерном массиве b хранится по строкам верхний треугольник квадратной матрицы (элементы, расположенные выше главной диагонали, включая главную диагональ). Напечатать его по строкам. Восстановить исходную матрицу, заполнив ее нижний треугольник нулями. Напечатать по строкам.
const int m = (n * (n + 1)) / 2;
int[] b = new int[m];
int[,] a = new int[n, n];
Console.WriteLine(«Введите верхний треугольник матрицы по строкам»);
Console.WriteLine(«Верхний треугольник по строкам»);
Источник: studopedia.su