К каким компьютерным средствам относится программа живая математика

Конференция: Современные формы организации учебной деятельности

Организация: МБОУ СОШ №2

Населенный пункт: Волгоградская область, г. Волжский

ИКТ совместно с MIMIO приставкой позволяют учителю создавать интерактивные объекты, эффективно работающие на уроке и позволяющие рационально использовать время. Нет необходимости постоянно вытирать доску и чертить необходимые фигуры, графики функций, записывать задания для устной и письменной работы учащихся.

В коллекции самой приставки более тысячи математических объектов: многогранники, тела вращения, координатные прямые и плоскость, окружность, треугольники и т.д. Их можно перетаскивать и клонировать. Чертежи получаются наглядными, аккуратными.

При построении сечений многогранников можно использовать режим записи самого процесса последовательного построения, что позволяет существенно экономить время на уроке.

Наглядным становится поэтапное объяснение материала в сочетании средств интерактивной доски и программы «Живая математика».

Живая Математика. Мастер-класс. Урок 1

Традиционный подход к преподаванию геометрии приводит к малой популярности этого предмета, особенно среди учащихся, далёких от математики. Наиболее очевидная причина этого заключается в том, что формулировки и доказательства теорем заучиваются, но не проверяются. Такой стиль обучения нацелен на развитие некритического, нетворческого мышления и естественно отторгается современными школьниками. Помочь решить возникающие в связи с этим проблемы может учебно-методический комплект (УМК) «Живая Математика», который сформирован на основе программы Geometry’s Sketchpad (в русском переводе «Живая Математика»), переведенной на русский язык и адаптированной Институтом новых технологий. Комплект был поставлен в школы-миллионеры Российской Федерации в рамках ПНПО.

Учебно-методический комплект состоит из самой программы «Живая Математика», методического пособия и альбомов готовых динамических чертежей, разделенных на две группы: «Теоремы и задачи школьного курса» и «Дополнительные материалы».

Первая группа «Теоремы и задачи школьного курса» включает альбом «Введение в компьютеризированный курс планиметрии», содержащий 46 уроков по темам: начальные геометрические сведения, треугольники, четырехугольники; площади, подобие, окружность.

Сама программа «Живая математика» представляет собой уникальный продукт, позволяющий строить современный компьютерный чертеж, который выглядит как традиционный, однако, представляет собой качественно совершенно новое явление. Чёртёж, построенный на бумаге с помощью карандаша и линейки, имеет важнейшее значение, но обладает двумя недостатками: требует затрат времени и конечный продукт оказывается статичным. Программа «Живая математика» позволяет значительно экономить время, но самое главное: чертёж, построенный с помощью программы, можно тиражировать, деформировать, перемещать и видоизменять. Элементы чертежа легко измерить компьютерными средствами, а результаты этих измерений допускают дальнейшую компьютерную обработку. Возможны также многократные обмены чертежами с учителем, хранение нескольких вариантов одного и того же чертежа и т. п. Появляется возможность добиваться от учащихся точных и грамотных письменных формулировок (по крайней мере, констатирующих то, что они видят); их можно переделывать столько раз, сколько требуется.

Как выучить математику во взрослом возрасте

УМК может использоваться практически при любых видах учебной деятельности, в том числе, при выполнении домашних работ, творческих проектов и т. д.

При работе в рамках данного УМК каждая обсуждаемая фигура изображается на экране монитора. При решении задач учащиеся могут выполнять задание на чертеже, приложенном к программе, а могут создавать собственные чертежи и сверять свои построения с образцом. Если же работа происходит в классе, оснащенном только одним компьютером и проектором, ученикам можно предложить выполнить решение в тетради, пользуясь при этом указаниями и подсказками, данными в задачах, и сверить свои построения с образцом.

Учителю математики, приступающему к работе в УМК, достаточно владеть компьютером на уровне начинающего пользователя. Сама программа «Живая Математика» легко осваивается при помощи руководства, содержащегося в первом разделе данного пособия. Учащиеся могут установить программу на домашний компьютер и работать с ней индивидуально во внеурочное время.

Из 26 учащихся 8В класса, в котором я работала, программа была установлена у 75% учащихся. Для того чтобы учащиеся получили первоначальные навыки работы в программе, достаточно 2-3 занятий. За это время можно изучить материал первых четырёх уроков сборника методических материалов. Я проводила занятия после уроков в компьютерном классе.

Причём, если на первом занятии присутствовало 6 учащихся, то на втором и третьем уже 11. Учащиеся, присутствующие на первом занятии, стали активными помощниками учителя на тех уроках геометрии, когда использовалась программа.

При помощи программы УМК «Живая математика» можно:

1. Объяснять сложные темы и изучать теоремы

Учебники геометрии содержат многочисленные определения, постулаты, теоремы, леммы, которые бывает нелегко понять или воспроизвести. При помощи «Живой Математики» удобно создавать конструкции, моделирующие условия теорем, и экспериментировать с ними. Альбом «Теоремы и задачи школьного курса» составлен в соответствии с учебниками Атанасяна Л.С. «Геометрия. 7-9 кл.» и «Геометрия.10-11кл».

Например, при изучении темы «Применение подобия к решению задач и доказательству теорем» в 8 классе рассматривается задача: какая фигура получится, если последовательно соединить середины сторон произвольного четырёхугольника?

Работаем следующим образом:

1. предлагаем учащимся построить произвольные четырёхугольники, причём как выпуклые, так и невыпуклые;
2. через команду «Середина» меню «Измерения» строим середины всех сторон четырёхугольника, последовательно их соединяем;
3. анализируем особенности полученной фигуры; возможно, уже сейчас учащиеся выдвинут предположения, что данная фигура является параллелограммом;
4. предлагаем проверить сохранение свойств внутренней фигуры при любой форме внешнего четырёхугольника – потянем туда-сюда вершины исходной фигуры;
5. для уточнения предположения с помощью меню «Измерения» вычисляем величины отдельных элементов внутренней фигуры и снова изменяем исходную фигуру, наблюдая, что происходит с измерениями;
6. окончательно формулируем гипотезу.

1. Оживлять рисунки из учебника

Получив определенный навык работы в «Живой Математике», нетрудно понять, что проще и быстрее воспроизвести рисунок из учебника на компьютере, чем рисовать его на бумаге. Одному из учеников каждый урок дается задание подготовить чертежи ко всем задачам домашней работы. При этом оценивается динамичность (существование чертежа со всеми своими возможными деформациями) и соответствие чертежа условиям задачи. В качестве дополнительного необязательного задания учащиеся могут подобрать задачи по изучаемой теме из дополнительных источников, подготовить чертежи.

Решать экспериментальные задачи . Задачи этого типа отличаются от задач на доказательство тем, что утверждение надо не только доказать, но и сформулировать. Экспериментируя с чертежом, учащийся формулирует гипотезы. После этого задача превращается в задачу на доказательство сформулированной гипотезы.

Например, при изучении темы «Площадь трапеции» полезно рассмотреть следующую задачу: площади каких трапеций равны полупроизведению их диагоналей. Обычно, таким образом сформулированные задачи ставят учащихся в тупик, они просто не знают с чего начать решение. Программа «Живая математика» позволяет сначала увидеть такую трапецию, а затем установить её свойства и сделать вывод.

Ход решения задачи:

1. строим произвольную трапецию;
2. через команду «Площадь» меню «Измерения» вычисляем площадь трапеции;
3. через встроенный калькулятор меню «Измерения» вычисляем величину, равную полупроизведению диагоналей;
4. двигаем вершины трапеции, добиваясь равенства величин, вычисленных в пунктах 2 и 3;
5. анализируем особенности трапеции, для которой равенство выполняется, выдвигаем предположение: угол между диагоналями прямой;
6. проверяем предположение: с помощью меню «Измерения» вычисляем угол между диагоналями.

При необходимости корректируем чертёж, двигая вершины трапеции, и формулируем ответ на вопрос задачи .

1. Применять программу в других разделах математики

Легко убедиться, что «Живая Математика» — незаменимый инструмент для изучения не только геометрии, но и вообще всех математических курсов, например, алгебры (тема «Функции и графики»).

1. Использовать во внеклассной работе по предмету Удивительные геометрические объекты — фракталы, которые моделируют сложные и красивые явления природы и поэтому являются элементом многих графических компьютерных программ. Фрактал — это самоподобный геометрический объект, который выглядит одинаковым образом при любом увеличении изображения . Построение фрактала включает в себя изготовление простой конструкции, которая формирует все меньшие и меньшие детали фигуры. Команда «Итерации» позволяет построить конструкции такого рода, впрочем, как и другие фигуры с повторяющимся алгоритмом построения элементов. Построение фракталов позволяет иллюстрировать не только интереснейшее геометрическое явление, но и привлечь учащихся к исследовательской работе, заинтересовать их в изучении геометрии на более высоком уровне, что способствует активизации познавательной деятельности учащихся.

Возможности программы поистине уникальны. Я работаю с программой не первый год, но уже не представляю, как раньше обходилась без неё. Предвижу вопрос скептиков: «А не тупеют ли дети, когда программа по одному щелчку мышки предлагает готовые решения и измерения?» Ответ прост: чтобы построить грамотный чертёж, нужно знать, как минимум, определения и свойства рассматриваемых фигур.

1.Живая математика. Электронное учебное пособие. — М. : Институт новых технологий, 2008. — 1 эл. опт. диск (CD-ROM)

2.Уроки математики с применением ИКТ. Методическое пособие с электронным приложением/ М.Н.Каратанова.-М: Планета,2010

Источник: www.pedopyt.ru

Информационно-коммуникационные технологии
в педагогическом образовании

Раздел: Материалы II Международной очно-заочной научно-практической конференции «Проблемы и перспективы современного физико-математического, информационного и технологического образования» (Новокузнецк, февраль 2018)

Журнал: Применение информационно-коммуникационных технологий в современном образовании

26 апреля 2018 г.

Авторы: Осипова Людмила Александровна , Позднякова Елена Валерьевна

Е. В. Позднякова, Л. А. Осипова

E. V. Pozdnyakova, L. A. Osipova

Позднякова Елена Валерьевна, кандидат педагогических наук, доцент, НФИ КемГУ, г. Новокузнецк.

Осипова Людмила Александровна, кандидат педагогических наук, доцент, НФИ КемГУ, г. Новокузнецк.

Pozdnyakova Elena Valerievna, candidate of pedagogical Sciences, associate Professor, NFI KemGU, Novokuznetsk.

Osipova Ludmila Alexandrovna, candidate of pedagogical Sciences, associate Professor, NFI KemGU, Novokuznetsk.

ОРГАНИЗАЦИЯ УЧЕБНЫХ ИССЛЕДОВАНИЙ ПО ГЕОМЕТРИИ НА ОСНОВЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «ЖИВАЯ МАТЕМАТИКА»

THE ORGANIZATION OF EDUCATIONAL RESEARCH IN GEOMETRY-BASED COMPUTER PROGRAM «LIVING MATHEMATICS»

Аннотация. Актуализируется проблема использования информационно-коммуникационных технологий в обучении математике. Рассматриваются возможности компьютерной программы «Живая математика» для организации учебных исследований учащихся по геометрии.

Annotation. Actualizarea the problem of the use of information and communication technologies in the teaching of mathematics. Discusses the possibilities of computer programs «Living mathematics» for the educational research of students in geometry.

Ключевые слова: учебное исследование, компьютерная программа «Живая математика», динамический чертеж, наблюдение и экспериментирование в геометрии.

Keywords: training study, computer program «Living mathematics», dynamic drawing, observation and experimentation in geometry.

В настоящее время в России идет становление новой системы образования. Этот процесс сопровождается существенными изменениями в педагогической теории и практике учебно-воспитательного процесса. Ведутся поиски новых эффективных методов обучения и таких методических приёмов, которые бы активизировали мысль школьников, стимулировали бы их к самостоятельному приобретению знаний. Немаловажная роль отводится информационным и телекоммуникационным технологиям, так как они позволяют решить проблему перехода от традиционной формы обучения, направленной на усвоение учеником фиксированной суммы знаний, к новой, где основной упор сделан на освоение способов деятельности.

Одно из основных назначений компьютера в обучении геометрии – исследование геометрических моделей.

Для использования на уроках геометрии существуют программы, предоставляющие ученику среду, в которой можно быстро, точно и красиво выполнять любые аналоги построений с помощью циркуля и линейки, а также вводить привычные обозначения, автоматически измерять длины отрезков и т. д. В таких программах можно не только строить аккуратные чертежи, но и видоизменять уже готовые, а также использовать анимацию.

Одной из подобных компьютерных программ является «Живая математика» – это компьютерная система моделирования, исследования и анализа широкого круга математических задач, поэтому она будет полезна при изучении не только геометрии, но и алгебры, тригонометрии, математического анализа. Она обладает возможностями (изменить фигуры, их взаимное расположение и размеры и т.д.), облегчающими выполнение перечисленных операций, стимулирующих в свою очередь развитие мышления школьников. Важно также, что в этой программе ученики работают фактически с целым семейством фигур, а не с отдельным его представителем, что способствует развитию геометрической интуиции детей.

Данная программа создаёт документы, содержащие математические чертежи, то есть графики и геометрические фигуры, при этом каждый чертеж конструируется из отдельных объектов. Интерактивное управление документами и объектами в них осуществляется с помощью сочетания инструментов и команд меню. Используемые в программе понятия и объекты делятся на геометрические (точка, прямая, луч, круг, дуга, геометрическое место точек, измерение и прочее) и числовые или алгебраические (параметр, координаты точки, функция и т.д.). К дополнительным объектам относятся надпись и исполнительная кнопка (нужны для описания, объяснения и представления результатов).

По сути, «Живая математика» – электронный аналог готовальни с дополнительными динамическими возможностями. Для выполнения чертежей используются стандартные геометрические операции: проведение прямой (луча, отрезка) через две точки, построение окружности по заданному центру и точке на окружности (или по центру и радиусу), биссектрисы угла, середины отрезка, проведение перпендикулярных и параллельных прямых, фиксирование точки пересечения прямых, окружностей, прямой и окружности.

Одно из главных достоинств «Живой математики» — возможность непрерывно изменять объекты, что создаёт предпосылки для развития компьютерного эксперимента [1].

Рассмотрим пример. Определите вид четырехугольника, вершинами которого являются середины сторон произвольного выпуклого четырехугольника АВСD.

Исследуйте, в каких четырехугольниках середины сторон являются вершинами: 1) прямоугольника; 2) ромба; 3) квадрата [2].

В компьютерной программе «Живая математика» учащиеся строят произвольный четырехугольник АВСD и отмечают середины его сторон К, L, M, N (рис. 1).

Изменяя форму и размеры четырехугольника АВСD, т. е. наблюдая геометрическую конфигурацию в динамике, учащиеся высказывают гипотезу о форме четырехугольника KLMN (KLMN – параллелограмм) Для доказательства гипотезы учитель предлагает построить диагональ АС (или ВD).

Продолжая экспериментирование с геометрической конфигурацией и наблюдая за изменением формы четырехугольников, учащиеся высказывают гипотезы:

1. Если АВСD – дельтоид или ромб, то KLMN – прямоугольник (рис. 2).
   
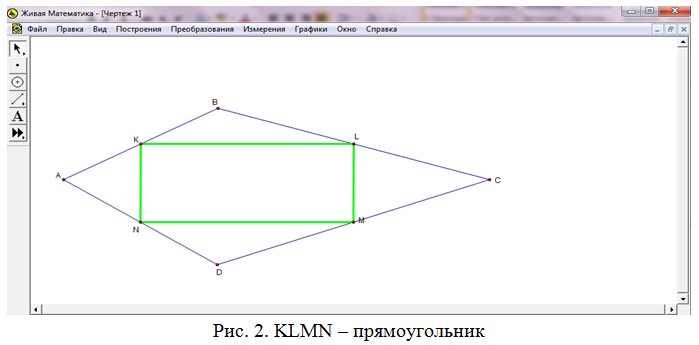
2. Если АВСD – прямоугольник или равнобедренная трапеция, то KLMN – ромб (рис. 3).
   
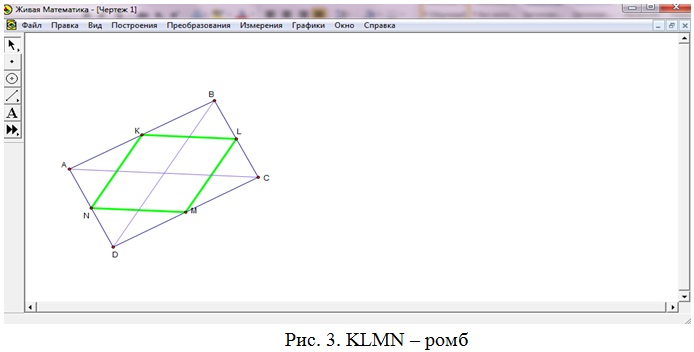
3. Если АВСD – дельтоид с равными диагоналями или квадрат, то KLMN – квадрат (рис. 4).
   

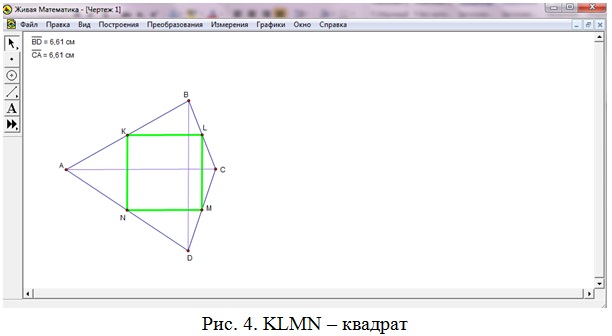
Возможность «Живой математики» создавать динамические чертежи и презентации позволяет экономить время, пробуждает и поддерживает устойчивый интерес и активизирует познавательную деятельность школьников.

Список литературы

1. Позднякова, Е. В. Организация учебных исследований школьников на основе компьютерной программы «Живая геометрия» [Электронный ресурс] / Е. В. Позднякова, Н. А. Жучкова // Современные проблемы науки и образования. – 2005. – № 1. – Режим доступа: https://science-education.ru/ru/article/ view?id=147 (дата обращения: 25.01.2018).
2. Цукарь, А. Я. Дидактические материалы по геометрии с элементами исследования для 8 класса [Текст] / А. Я. Цукарь. – М.: Просвещение, 1999. – 80 с.

Издатель журнала: Можаров Максим Сергеевич

Источник: infed.ru

Внеурочных занятия по математике«Живая Математика»

Сама программа «Живая математика» представляет собой уникальный продукт, позволяющий строить современный компьютерный чертеж, который выглядит как традиционный, однако, представляет собой качественно совершенно новое явление. Чертеж, построенный на бумаге с помощью карандаша и линейки, имеет важ нейшее значение, но обладает двумя недостатками: требует затрат времени и конечный продукт оказывается статичным. Программа «Живая математика» позволяет значительно экономить время, но самое главное: чертёж, построенный с помощью программы, можно тиражировать, деформировать, перемещать и видоизменять. Элементы чертежа легко измерить компьютерными средствами, а результаты этих измерений допускают дальнейшую компьютерную обработку. Возможны также многократные обмены чертежами с учителем, хранение нескольких вариантов одного и того же чертежа и т. п.

При работе в рамках данного УМК каждая обсуждаемая фигура изображается на экране монитора. При решении задач учащиеся могут выполнять задание на чертеже, приложенном к программе, а могут создавать собственные чертежи и сверять свои построения с образцом. Если же работа происходит в классе, оснащенном только одним компьютером и проектором, ученикам можно предложить выполнить решение в тетради, пользуясь при этом указаниями и подсказками, данными в задачах, и сверить свои построения с образцом.

Реализация компетентностного подхода на занятиях математического кружка способствует активизации познавательной деятельности учащихся, повышению интереса к предмету, нацеливает ученика на конечный результат: самостоятельное приобретение конкретных умений, навыков учебной и мыслительной деятельности.

Вызывая интерес учащихся к предмету, кружки способствуют развитию математического кругозора, творческих способностей учащихся, привитию навыков самостоятельной работы и тем самым повышение качества математической подготовки учащихся.

Внеучебное занятие является одной из форм обучения математике, позволяющий развивать ценностно-смысловую, общекультурную, учебно-познавательную, информационно-коммуникативную, социально-трудовую компетенции и компетенции личностного самосовершенствования учащихся. Это обуславливается следующими факторами: во-первых, кружковая форма работы является доступной для всех школ, так как ее реализация не требует больших материальных затрат и специального оборудования, за исключением компьютеров, и позволяет охватить достаточно большее количество учащихся; во-вторых, по форме проведения внеучебные занятия являются схожими с урочными, в то же время они имеют большие возможности, по сравнению с урочными занятиями, в приобщении учащихся к новым формам работы: лекциям, лабораторным и практическим работам и другим. По мнению А.В. Фаркова, внеучебное занятие — это самодеятельное объединение учащихся под руководством педагога, в рамках которого проводятся систематические занятия с учащимися во внеурочное время [9,C.4]. Хорошо организованные занятия обеспечивают проявление интереса к математике, развивают творческие способности учащихся, поднимают общую математическую культуру и способствуют повышению успеваемости при изучении программного материала.

Требования, предъявляемые программой по математике, школьными учебниками и сложившейся методикой обучения, рассчитаны на так называемого «среднего» ученика. Однако уже с первых классов начинается резкое расслоение коллектива учащихся: на тех, кто легко и с интересом усваивают программный материал по математике, на тех, кто добивается при изучении математики лишь удовлетворительных результатов, и тех, кому успешное изучение математики дается с большим трудом.

Проведение внеклассной работы по математике является прекрасным средством повышения квалификации учителей. Одной из целей является расширение изучаемого материала курса математики, иногда такое расширение выходит за рамки обязательной программы. Рассмотрение на дополнительных занятиях таких вопросов неизбежно приводит учителя к необходимости основательного знакомства с этим материалом и с методикой его изложения учащимся.

Обычно занятия организуются для хорошо успевающих учащихся. Однако следует иметь в виду, что иногда и слабо успевающие учащиеся изъявляют желание участвовать в работе математического занятия и нередко весьма успешно занимаются там, учителю математики не следует этому препятствовать. Необходимо лишь более внимательно отнестись к таким учащимся, постараться укрепить имеющиеся у них ростки интереса к математике, проследить за тем, чтобы работа в математическом кружке оказалась для них посильной. Конечно, наличие слабо успевающих учащихся среди учащихся затрудняет работу учителя, однако путем индивидуализации заданий, предлагаемых учителем, можно в некоторой степени ослабить эти трудности.

Уже при организации математического кружка необходимо заинтересовать учащихся, показать им, что работа в кружке не является дублированием классных занятии, четко сформулировать цели и раскрыть характер предстоящей работы (для этого целесообразно выделить часть времени на одном из уроков математики с тем, чтобы обратиться с сообщением об организации занятий ко всему классу).

Занятия целесообразно проводить один раз в неделю, выделяя на каждое занятие по одному часу. К организации работы математического занятия целесообразно привлекать самих учащихся (поручать им подготовку небольших сообщений по изучаемой теме, подбор задач и упражнений по конкретной теме, подготовку справок исторического характера, изготовление моделей и рисунков к данному занятию и т. д.).

Источник: znanio.ru