К числу недостатков программы geogebra можно отнести следующие

GeoGebra — вычислительная программа на компьютер для математических вычислений любого уровня образования, объединяющая в себе геометрию с алгеброй, электронные таблицы и графику, вычислительную статистику.

GeoGebra — это не просто многофункциональная математическая программа для компьютера, это мировое сообщество миллионов пользователей, которое активно растёт.

Динамическое ПО от разработчиков GeoGebra, которые поддерживают науку и передовые технологии, инновационные инфо-продукты и математическое образование. Утилита связывает геометрию и алгебру в визуально понятной форме. Математика это не только формула на листе бумаги, с ГеоГебра её можно ощущать визуально. Для учителей это неотъемлемый помощник по ходу обучения.

Основные возможности GeoGebra:

• построение графиков функций, кривых, параметрических координат, конических сечений;
• создание окружностей по радиусу и трём точкам, эллипсов, парабол, гипербол;
• моделирование 3D-объектов;
• сложение и умножение матриц;
• транспортирование, инвертирование, вычисление определителя и комплексных чисел;
• нахождение точек пересечения кривых и другие.

Скачать GeoGebra бесплатно на русском

Загрузить утилиту можно абсолютно бесплатно с официального сайта разработчика по ссылкам ниже.

Применение программы GeoGebra для нахождения угла между прямыми в пространстве

В ГеоГебра доступны дополнительные функции:

1. Статическое вычисление математического ожидания или дисперсии, а также коэффициента корреляции.
2. Аппроксимация нескольких точек в кривой по заданному виду.
3. Работа с таблицами и анимацией, ввод команд.
4. Доступны инструменты редактирования Перо, Удаление, Полигон и другие.

С GeoGebra можно создавать вычисления онлайн и строить сложные графики прямо на сайте. Прямая ссылка доступна ниже.

Рекомендуется скачать GeoGebra бесплатно на русском языке для того, чтобы создавать Java-апплеты на динамических чертежах, а после включать их на сайты (html-страницы). С официального сайта можно подгрузить бесплатно готовые шаблоны в формате ggb прямо в ГеоГебру.

Возникали ли у вас необходимость построить график функции? Поможет бесплатная программа по математике GeoGebra. Она анализирует функции, решает задачи, строит графики. Рассмотрим подробно, как установить, скачать и работать с этой программой.

Что это такое

GeoGebra — программа по математике. Написана на языке программирования Java. Разработана Маркусом Хохенвартером. Приложение не ограничивается только работой с графиками. Используйте ее для создания чертежей, решении задач по геометрии, разработке анимации.

Инструкция по работе в программе Geogebra

Позволяет наглядно обучаться математике.

• Создание графика в Word;
• Как работать с рисованной анимацией.

Решает такие задачи:

1. Обучение алгебре и геометрии;
2. Создание графиков и таблиц;
3. Работа со статическими данными;
4. Анимация;
5. Создание 2D, 3D фигур;
6. Создание интерактивных роликов с последующим размещением в интернет.

• сохраните форматом GeoGebra;
• распечатайте;
• экспортируйте в форматах SVG, PNG, PDF.

По адресу: https://wiki.geogebra.org/ru/Руководство находится руководство пользователя, с информацией про работу с объектами.

Как скачать

Официальный сайт находится по адресу: http://www.geogebra.org . Программу можно скачать и установить на ПК. Также разработчики предлагают online использование. Чтобы скачать нажимаем ссылку «Загрузки». Будет предложено два варианта:

1. Graphing Calculator. Используйте ее для решения уравнений, нахождение специальных функций, возможность поделиться результатами с другими людьми;
2. Geometry. Для создания геометрических фигур, рисования.

1. Скачать приложения для ОС Windows, Mac бесплатно на русском.
2. Установить расширения в браузер Chrome,
3. Загрузить приложения для работы на смартфонах и планшетах.

Скачиваем инсталляционный «exe» файл. Нажимаем по нему мышкой два раза для начала загрузки. Установка простая, не вызовет сложностей даже у начинающий пользователей.

Интерфейс

Напоминает графический редактор. Рассмотрим его основные элементы:

1. Кнопка меню (три горизонтальные линии). Используйте для изменения настроек;
2. Панель инструментов. Для создания фигур и графиков;
3. Стрелки отменяющие действия;
4. Рабочая область. Все действия происходят в ней. При помощи колеса мыши редактируйте масштаб.

Чтобы настроить приложение для работы, сделайте следующее. Нажимаем кнопку настроек (три горизонтальные линии)-«Apps». Выбираем необходимое: калькулятор, геометрия, 3D. Рассмотрим некоторые возможности программы.

Как построить график

Выбираем в настройках «Apps»-«Графический калькулятор». Действия происходят в поле ввода. Например, построим параболу. Прописываем: x^2. Или используйте кнопки внизу программы.

Нажимаем «Enter». На рабочей области построится график.

Добавляйте переменные. Пропишите их в строку формулы.

Как создать 3D

В настройках переходим «Apps»-«3D». Выбираем инструменты кликнув по иконке. Далее постройте объект следуя подсказкам. Выполняем нужные действия.

GeoGebra online на русском

Не хотите загружать дополнительный софт? Используйте онлайн (online) версию, расположенную по адресу: https://www.geogebra.org/classic . Единственное условие необходимое для работы — наличие интернет.

Вывод

GeoGebra с широким функционалом, предназначена для обучения алгебре и геометрии. Если не удалось установить ее на ПК, используйте online версию. Мне кажется она удобнее. Остались вопросы, инструкция по работе с GeoGebra поможет разобраться детальнее.

GeoGebra – уникальная программа по математике. Она написанная и усовершенствованная на программном языке Java. Это приложение не ограничивается одной лишь графикой, а имеет в себе множество опций. В основному, GeoGebra используется для различных чертежей, для решений задач по геометрии и их аккуратного оформления.

Готовый материал, который прошел GeoGebra можно распечатать, сохранить специальным форматом GeoGebra или же экспортировать на нужный носитель информации.

Скачать бесплатно GeoGebra 6.0.564

GeoGebra 6.0.541 Repack

GeoGebra 6.0.535 Repack

Пароль ко всем архивам: 1progs

Видео по установке GeoGebra

GeoGebra поможет решить такие задачи:

• обучит математическим наукам;
• создаст идеальные графики, а также таблицы;
• создаст сложную многофункциональную анимацию;
• создаст яркие интерактивные ролики с последующим размещением в интернете.

Программу GeoGebra можно скачать бесплатно на русском языке. Также разработчики предлагают использование программы в режиме online. Classic GeoGebra устанавливается, как и обычный файл и сохраняется на указанном диске. 3D–графики идеально смотрятся в распечатанном виде или же на сенсорной доске.

Также приложение можно скачать на телефон или же планшет. Это никаким образом не скажется на скорости работы. Можно потом готовый файл сбросить на компьютер или же просто распечатать с телефона.

Скачать торрент GeoGebra 6.0.564 3D на русском

Аналоги программы

Похожие программы смотрите в наших подборках программ

Программы для обучения

Используемые источники:

• https://soft-file.ru/geogebra/
• https://public-pc.com/instruktsiya-po-rabote-s-geogebra/
• https://1progs.ru/geogebra/

Источник: ztegid.ru

GeoGebra – самая популярная в мире математическая программа.

GeoGebra — самая популярная в мире бесплатная математическая программа. С помощью обучающей программы по математике, можно будет выполнить множество полезных вещей: анализировать функции, строить графики, решать задачи, работать с функциями и т. д.

Интерфейс программы GeoGebra (ГеоГебра) напоминает классную доску, на которой можно рисовать графики, создавать геометрические фигуры и т. п. В окне программы будет наглядно отображены производимые изменения: если вы измените уравнение, кривая перестроится, изменится масштаб или ее положение в пространстве, уравнение, написанное рядом с кривой, автоматически будет скорректировано, согласно новым значениям.

Программу GeoGebra широко используют в мире миллионы пользователей для обучения алгебре и геометрии. Процесс обучения нагляден благодаря визуальной форме использования приложения.

Возможности программы по математике не ограничиваются только построением графиков, программу GeoGebra можно будет использовать для интерактивных чертежей при решении геометрических задач.

Программа ГеоГебра обладает мощными и функциональными возможностями, которые позволяет наглядно и просто обучаться математике. «>

Приложение включает в себя геометрию, алгебру, есть возможность совершать арифметические операции, создавать таблицы, графики, возможна работа со статистикой, работа с функциями, поддерживается создание анимации и т. д. В программе GeoGebra можно будет создавать различные 2D и 3D фигуры, интерактивные ролики, которые затем можно будет размещать в интернете.

Все приложения, входящие в состав программы GeoGebra, доступны и синхронизируются между собой для работы в составе одного пакета.

GeoGebra была создана Маркусом Хохенвартером. Программа написана на языке Java, приложение поддерживает работу в различных операционных системах: Windows, Mac OS X, Linux, Android.

С сайта производителя можно будет скачать обычную версию программы GeoGebra для установки на компьютер. Также можно будет скачать переносную версию программы (GeoGebra Portable) для соответствующей операционной системы.

geogebra скачать

После запуска GeoGebra на компьютере, ознакомимся с интерфейсом программы.

Интерфейс GeoGebra

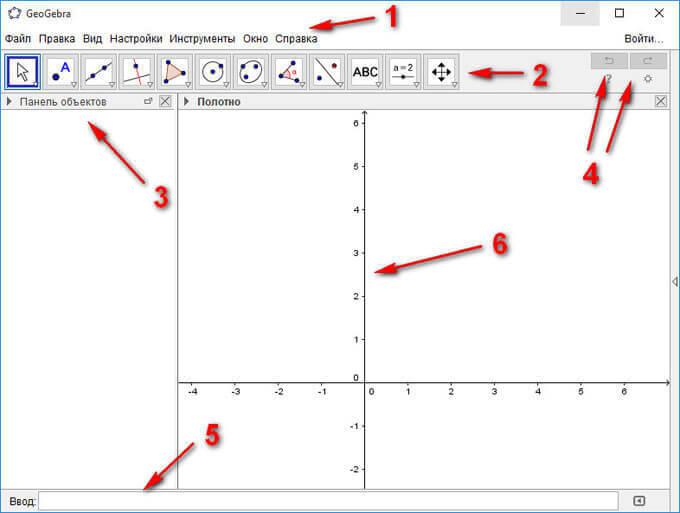
Интерфейс программы GeoGebra напоминает графический редактор. Программу можно использовать для черчения, но это не основное предназначение приложения.
Давайте рассмотрим основные элементы интерфейса программы GeoGebra:

1. Полоса меню. Из меню вы можете изменить настройки программы.
2. Панель инструментов. Здесь находятся инструменты для создания объектов. После щелчка по треугольнику в правом нижнем углу кнопки, будут открыты дополнительные инструменты. Операции, доступные в панели инструментов, можно производить с помощью строки ввода.
3. Панель объектов. В Панели объектов отображаются введенные переменные и функции. Вместо имен переменных здесь отображаются их значения. Для того, чтобы увидеть формулу в символьном виде, нужно будет кликнуть по ней правой кнопкой мыши.
4. Кнопки «Отменить» и «Повторить».
5. Строка ввода. Это основной инструмент при работе в программе GeoGebra. Здесь вводятся команды и формулы, задаются значения переменных. Справа от строки ввода расположена кнопка «Список команд». С помощью дополнительных команд можно будет вводить команды и отсутствующие на клавиатуре символы.
6. Рабочая область. Все построения в программе производятся в рабочей области. Вы можете изменить масштаб с помощью колесика мыши, перемещать по рабочей области ось координат.

Далее попытаемся выполнить некоторые элементарные действия в программе GeoGebra.

Построение графика функции в GeoGebra

Для построения графика функции достаточно будет набрать ее в поле ввода. Для отображения параболы нужно будет написать в строке «Ввод» следующее выражение:

Символ «^» в программе GeoGebra обозначает возведение в степень.

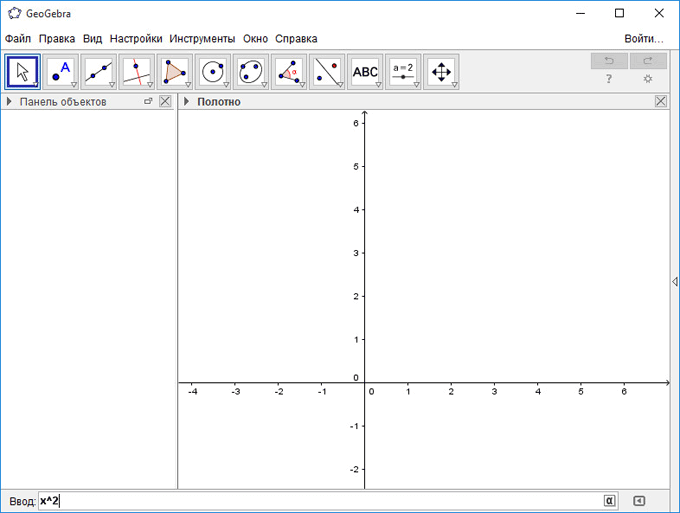
Далее нажмите на кнопку «Enter». После этого в рабочей области будет построен график. Рисунок можно будет масштабировать с помощью колесика мыши. Для перемещения рабочей области нужно будет нажать на клавишу «Shift», одновременно удерживая нажатой левую кнопку мыши.

Вы можете перемещать сам график при помощи нажатой правой кнопки мыши, при этом, в Панели объектов будут отображены изменения в уравнении.

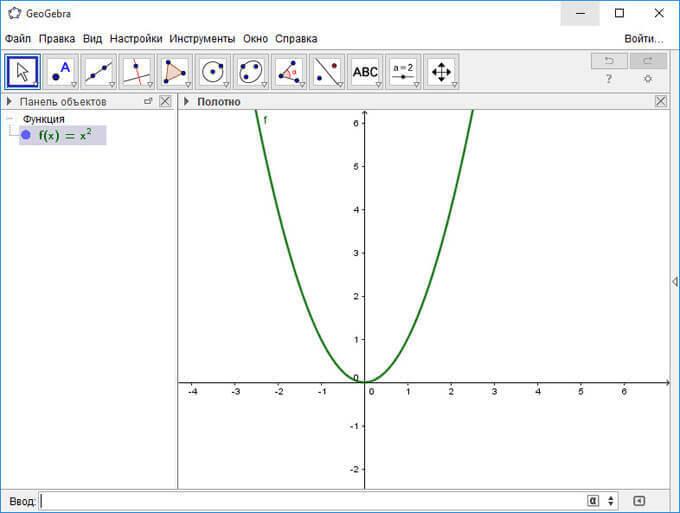
Вы можете добавить в уравнение переменные параметры, например, следующие (введите их строку ввода поочередно):

a=1
b=1
(x+a)^2+b

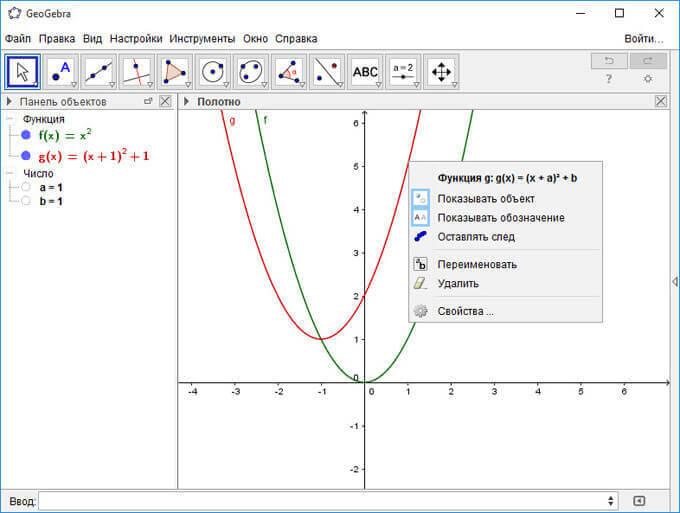
В рабочей области появится еще одна парабола, смещенная влево на одну единицу. Кликнув по графику, вы можете из открывшегося контекстного меню производить необходимые действия.

Создание треугольника в GeoGebra

Давайте попробуем начертить треугольник в программе GeoGebra. Для этого нужно будет перейти в «геометрический» режим для того, чтобы включить отображение сетки, и отключить отображение оси координат.

Кликните правой кнопкой мыши по оси координат, в контекстном меню выберите пункт «Сетка», а затем там кликните по пункту «Оси» для отключения оси координат. На панели инструментов нажмите на кнопку «Многоугольник».

После этого нарисуйте треугольник, последовательно установив три вершины. При необходимости, вы можете ввести точные координаты. Для этого вам нужно будет кликнуть по точке правой кнопкой мыши.

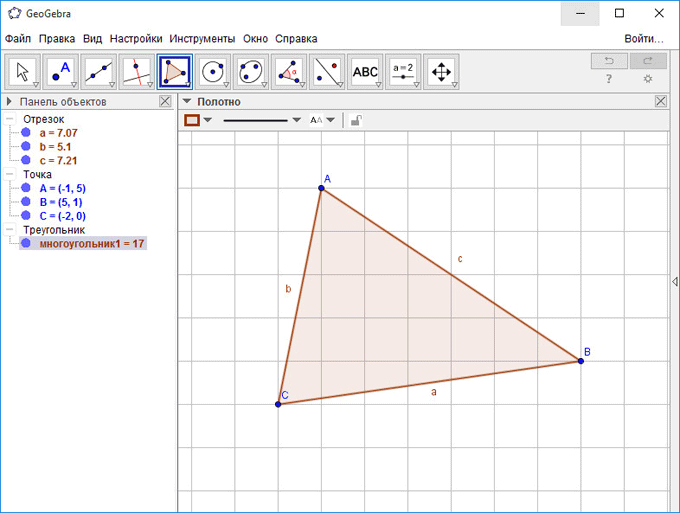
Далее вы можете создать биссектрису угла. Для этого нажмите на треугольную кнопку под кнопкой «Перпендикулярная прямая», а затем выберите из выпадающего списка инструмент «Биссектриса угла». После этого, кликните по двум отрезкам образующих угол, биссектриса будет создана.

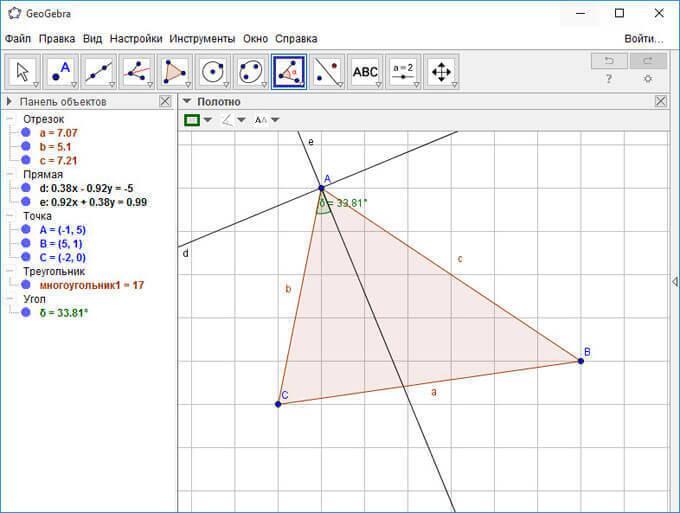
Вы можете обозначить угол. Для этого нажмите на кнопку инструмента «Угол» в Панели инструментов. Для отображения интересующего вас угла выберите три точки или две прямые.

Geogebra online

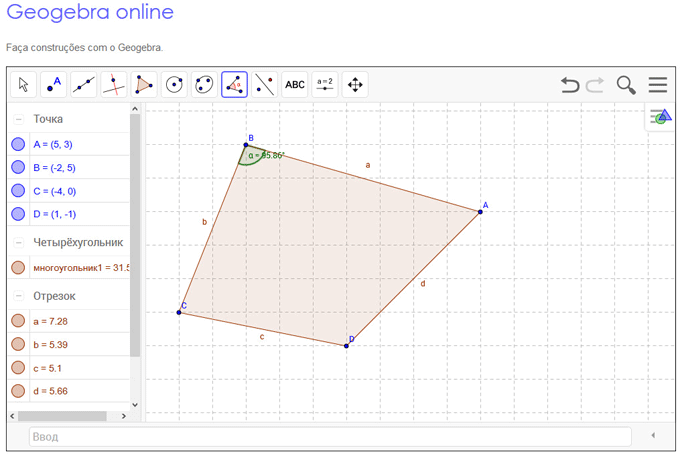
У программы GeoGebra имеется онлайн версия: Geogebra online (ГеоГебра онлайн). После перехода на сайт www.geogebra.org , вы можете открыть программу GeoGebra в своем браузере для выполнения необходимых действий. Таким образом, даже не устанавливая программу GeoGebra на свой компьютер, при наличии интернета, вы можете работать в этой математической программе, войдя на онлайн сервис со своего мобильного устройства.

Расширение GeoGebra

Создано расширение GeoGebra для браузера Google Chrome. Обратите внимание на количество пользователей расширения: более 2.6 миллиона человек. Немногие расширения из магазина Chrome могут сравниться с такими цифрами. Это свидетельствует о том, что приложение GeoGebra широко используется в мире для образовательных целей.

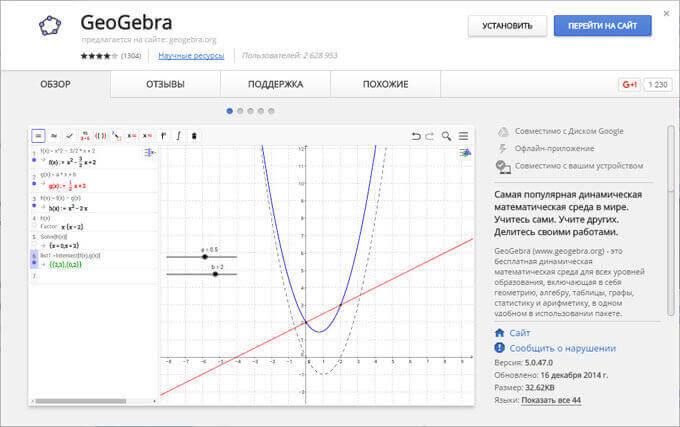
Для входа в расширение кликните по кнопке «Сервисы» на панели закладок в браузере Google Chrome. После этого будет открыто окно расширения GeoGebra в вашем браузере. На начальном экране вы можете выбрать раздел математики, с которым далее вы будете работать в приложении.

Дополнительные материалы по работе в программе, вы можете найти на сайте производителя приложения, и в интернете.

Заключение

Бесплатная программа GeoGebra предназначена для обучения математике. С помощью программы GeoGebra (ГеоГебра) можно обучаться или работать в динамической математической среде, включающей в себя геометрию, алгебру, другие разделы, с широкими функциональными возможностями.

Оригинал записи и комментарии на LiveInternet.ru

Источник: spayte.livejournal.com

К числу недостатков программы geogebra можно отнести следующие

Изучение графиков и функций можно сделать более эффективным, если при обучении использовать новые информационные технологии: они позволяют сократить время на рисование графиков на доске с мелом, изобразить график с невероятной точностью, сделать более наглядным изучение данной темы и много других преимуществ. В статье рассказывается об использовании новых информационных технологий на примере программы GeoGebra при изучении темы «Простейшие преобразования графиков», приводятся примеры построения графиков, также рассматривается построение взаимно обратных функций. Подробно описаны возможности использования программы GeoGebra при изучении простейших преобразований графиков, а также приведены преимущества перед использованием классических методов обучения. Даны примеры преобразования графиков с использованием программы GeoGebra, их описание и изучение свойств данных преобразований.

простейшие преобразования графиков
облачные технологии

1. Алексанян Г.А. Применение облачных сервисов в организации самостоятельной деятельности студентов СПО // Актуальные проблемы современной науки: свежий взгляд и новые подходы, I Международная научно-практическая конференция. Часть 2. – Йошкар-Ола, 2012. – С. 16-19.

2. Об утверждении федерального государственного образовательного стандарта среднего общего образования: Приказ Министерства образования и науки РФ от 17 мая 2012 г. № 413 (с изменениями и дополнениями) [Электронный ресурс]. – URL: http://base.garant.ru/70188902/#ixzz4mecRrm4P (дата обращения: 12.07.2017).

3. Санина Е.И. Обобщение и систематизация знаний по геометрии в средней школе в контексте технологического подхода к обучению: монография / Е.И. Санина, Е.Н. Буншафт. – Тула: Арт-Принт, 2012. – 259 с.

4. Алексанян Г.А. Развитие самостоятельной деятельности студентов СПО при использовании ИКТ в обучении математике // Международный научно-исследовательский журнал. Екатеринбург. – 2012. — № 3 (3). – С. 59-64.

5. Алгебра и начала анализа: учебник для 10-11 классов общеобразовательных учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. – 4-е изд. – М.: Просвещение, 2017. – 463 с.

6. Официальный сайт программы GeoGebra [Электронный ресурс]. – URL: https://www.geogebra.org/?lang=ru (дата обращения: 12.07.2017).

7. Терехова Н.Н. Эффективная методика преподавания темы «Простейшие преобразования графиков» // Открытый урок «Первое сентября» [Электронный ресурс]. – URL: http://festival.1september.ru/articles/566076/ (дата обращения: 12.07.2017).

8. Алексанян Г.А. Создание мультимедийной среды для студентов с применением облачных технологий и программы GeoGebra // Научный вестник филиала Кубанского государственного университета. – 2013. – № 3. – С.105-109.

9. Маринченко К.Е. Формирование профессиональной компетентности будущих специалистов на основе сетевых учебно-методических комплексов: дис. … канд. пед. наук: 13.00.08 – теория и методика профессионального образования. — Волгоград, 2009. – 185 с.

Информационные технологии позволяют переосмыслить применение Интернета в учебном процессе: от получения доступа к образовательным материалам различного вида (текстовым, визуальным, мультимедийным) до выполнения работы совместно с преподавателем или группой [1]. Быстро развивающиеся сервисы облачных вычислений предоставляют широкий спектр полезных приложений в обучении. Использование облачных сервисов и программы динамической геометрии рассмотрим на примере изучения темы «Простейшие преобразования графиков», которая предполагает следующие этапы обучения:

• Изучение новой темы с использованием программы GeoGebra.
• Тестирование, после которого проводится диагностика усвоения материала обучающимися, что позволяет подобрать каждому из них индивидуальные задания, направленные на устранение недостаточно изученных разделов темы. Это позволяет индивидуализировать самостоятельную деятельность, что способствует более эффективному овладению материалом.
• На основе результатов тестирования составляются совместно со обучающимися индивидуальные практические задания. Обучающимся предлагаются индивидуальные самостоятельные работы, формой контроля может служить web-проект, выполненный в среде GeoGebra и размещенный на персональной странице.

Знакомство с простейшими преобразованиями графиков начинается в 7 классе при изучении темы «Взаимное расположение графиков линейных функций». В 8 классе рассматриваются функции 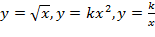, построение и преобразование их графиков функций. С помощью преобразований строятся функции вида .

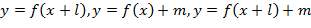При этом каждое преобразование изучается отдельной темой, в результате чего у обучаемых не формируется целостное представление о преобразованиях. А в 9 классе к этому списку добавляются и числовые функции, на примере степенных функций и функции вида 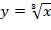, что окончательно запутывает обучаемых. В то же время выполнение простейших преобразований графиков необходимо при решении различных задач, в частности при нахождении области определения или множества значения функции, а также при решении уравнений и систем уравнений графическим методом [2].

Целесообразнее всего будет изучать все возможные преобразования графиков одновременно. Для этих целей наиболее эффективным средством изучения являются программы динамической геометрии.

Возможности применения программ динамической геометрии многочисленны. При помощи данных программ можно создавать заготовки с заданиями и высылать на электронные адреса учащихся или публиковать на сайте с разграничением доступа обучающихся. Также можно использовать апплеты при рассмотрении темы, создавая динамические построения геометрических объектов. Программа имеет возможность просмотра хода построений и выполнения задания, что позволяет выявить правильность выполнения учащимися построения или решения задачи и определить, чему из пройденного материала следует больше уделить внимание. Эффективнее всего будет создание коллекции апплетов на каждую из тем, причем в создании данной коллекции могут принимать участие и сами обучающиеся [3].

Для наших задач наиболее подходящим решением является свободно распространяемая программа GeoGebra.

У программы GeoGebra:

• хорошо продуманный интерфейс;
• совмещает в себе возможности выполнения построений и аналитическую геометрию;
• встроенный язык, при помощи которого можно задавать построения и производить математические расчеты;
• активное сообщество пользователей по всему миру (190 стран), институты GeoGebra [4].

Перечислим основные возможности программ динамической геометрии:

• строить точки, прямые, лучи, отрезки, окружности;
• построение комбинаций базовых фигур: углы, многоугольники, части круга и пр.;
• построение отрезков и углов заданной величины;
• предоставление инструментов для построения перпендикулярных и параллельных прямых, а также биссектрисы угла;
• выполнение параллельного переноса, симметрии, поворота и гомотетии фигур;
• деформирование фигуры или отдельных её частей;
• вычисление длины отрезка, величины угла, периметра и площади многоугольников, длины окружности и площади круга;
• осуществление анимации фигуры или отдельных её точек;
• выполнение итерации с геометрическими и алгебраическими объектами [4].

Рассмотрим возможности применения программы GeoGebra при изучении темы «Простейшие преобразования графиков».

Для того чтобы правильно построить график какой-либо функции, нужно сначала распознать заданные в формуле преобразования. Каждое отдельно взятое математическое действие в формуле задаёт отдельный вид преобразований. Поэтому сколько в формуле действий, столько и преобразований нужно будет выполнить над графиком элементарной функции. GeoGebra позволяет моментально изобразить преобразования графика при изменении параметров преобразования.

Например, дана функция: y=(x+2) 2 –3 [5].

Для того чтобы построить график этой функции, надо сначала построить график функции y=x 2 , затем переместить ее на 2 единицы влево по оси абсцисс и на 3 единицы вниз по оси ординат, следовательно, для наглядности построения нужно построить три графика, что перегружает чертеж и путает учащихся. А в том случае, когда поменяется хотя бы один из параметров, приходится перечертить весь график, что весьма не эффективно и отнимает массу времени. Все эти проблемы можно решить, используя программу GeoGebra. Для того чтобы изобразить преобразования графика функции y=(x+2) 2 –3 в GeoGebra, нужно всего лишь построить график y=(x+a) 2 –b при начальных значениях a=0 и b=0, затем, изменяя значения параметров a и b, следить за преобразованиями графика данной функции, при этом если построить график функции y=(x+a) n –b, можно менять еще и значение показателя данной функции, что еще больше углубит знания о преобразованиях функции при изменении различных параметров (рис. 1).

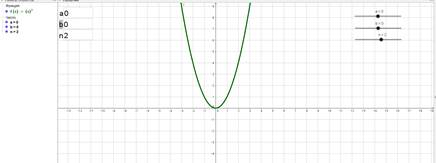
Функция y=(x+a) n +b при n=2, a=0, b=0

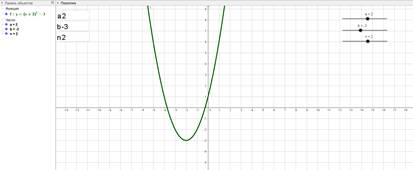
Функция y=(x+a) n +b при n=2, a=2, b=3

Рис. 1. Преобразование графика функции y=x 2

Для того чтобы изменить параметры, следует всего лишь ввести значение параметра и нажать клавишу «Enter» или передвинуть ползунок в соответствующее положение, при этом график моментально отображает заданное преобразование. Это позволяет наглядно и оперативно показывать преобразования графика, не тратя время на лишние построения. Преимуществами применения GeoGebra при построении данного графика являются: точность построения, чего невозможно добиться при изображении графика на обычной доске, а также возможность моментального изменения функции (например, квадратной на кубической или четвертой степени и т.д.), не тратя время на новые построения (рис. 2) [6].

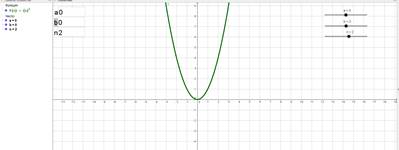
Функция y=(x+a) n +b при n=2, a=0, b=0

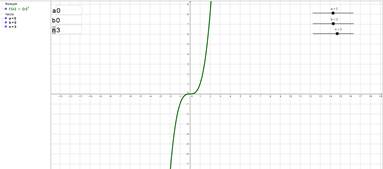
Функция y=(x+a) n –b при n=3, a=0, b=0

Рис. 2. Преобразование графика функции y=x n

Соответственно тут же можно показать преобразования данного графика при изменении соответствующих параметров.

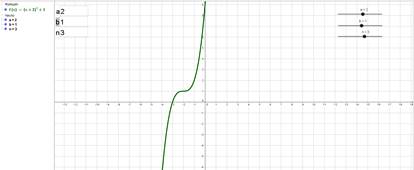
Рис. 3. Функция y=(x+a) n –b при n=3, a=2, b=1

Так же можно изобразить график любой функции. Например, нужно показать преобразование функции y=sinx. Выполним преобразование вида y=sin2x+1. Для того чтобы построить график этой функции, надо сначала построить график функции y=sinx, затем переместить ее на 1 единицу вверх по оси ординат, а умножение аргумента на 2 сжимает синусоиду в два раза.

Для построения данного графика необходимо построить график функции y=sinax+b при начальных значениях a=0 и b=0, затем, изменяя значения параметров a и b, следить за преобразованиями графика данной функции. Пошаговое изменение параметров позволяет выявить как ведет себя график при том или ином значении параметра, что способствует усвоению влияния параметров преобразования на графике и свойствах самой функции. Таким образом, становится понятно, что для получения графика y=sin2x+1 необходимо сделать два преобразования (рис. 4):

— умножение на 2 – сжимает синусоиду в два раза;

— прибавление 1 – поднимает синусоиду на одну единицу.

Проделав данные преобразования, получаем график искомой функции, попутно рассмотрев свойства и графики промежуточных функций. Данную заготовку также можно использовать для рассмотрения других преобразований, не тратя время на дополнительные построения, что экономит время на занятии и при подготовке к нему. Использование GeogGebra придает красочность и точность чертежу.

Рассматривая данные примеры, учащиеся сами могут прийти к выводу, что все преобразования можно разделить на:

— растяжение от оси Ox или сжатие к оси Ox;

— преобразование симметрии относительно оси Ox;

— параллельный перенос вдоль оси Ox;

— растяжение от оси Oy или сжатие к оси Oy;

— преобразование симметрии относительно оси Oy;

— параллельный перенос вдоль оси Oy.

Таким образом, рассмотрение данных примеров сходится к нахождению основной функции и выявлению преобразований, произведенных над ней [7].

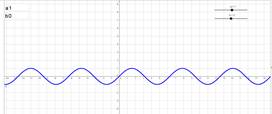
Функция y=sinax+b, при a=1, b=0

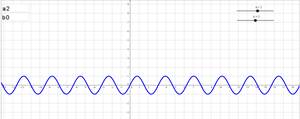
Функция y=sinax+b, при a=2, b=0

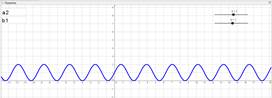
Функция y=sinax+b, при a=2, b=1

Рис. 4. Преобразование графика функции y=sinx

Построив таким образом несколько графиков, можно скрывать с чертежа и возвращать назад на экран сразу несколько изображений посредством панели объектов, которая находится в левой части окна программы.

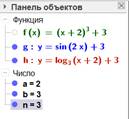
Рис. 5. Панель объектов программы GeoGebra

Данная функции программы GeoGebra позволяет сравнить график логарифмической функции с другими, например с показательной. И учащиеся наглядно видят, что логарифмическая и показательная функции являются взаимно обратными (рис. 6).

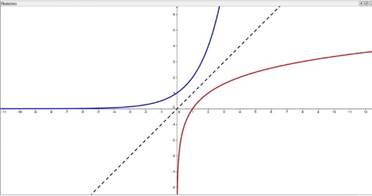
Рис. 6. Взаимно обратные функции

Очевидно, что подобным образом можно рассматривать и другие функции. При этом на полотно графики удобно выводить по одному, чтобы учащиеся сами приходили к выводу [8].

Знакомство с новым материалом, таким образом, становится более увлекательным и наглядным, учащиеся с удовольствием участвуют в проведении урока и отмечают изменившиеся свойства функции.

Использование программы GeoGebra ускоряет процесс обучения, позволяет точно и наглядно изображать преобразования графиков различных функций и дает возможность учащимся участвовать в процессе обучения, при этом экономя время на лишние построения. Также следует отметить, что данная методика развивает не только математические познания, но и навыки использования новых информационных технологий, что является важным критерием для современного выпускника. Использование GeoGebra не следует ограничивать только при проведении лекции, можно дать домашнее задание: построение различных графиков функции и их преобразований в программе GeoGebra, что будет способствовать закреплению изученного материала.

После изучения новой темы обучающиеся переходят ко второму этапу тестирования с применением сервиса UzTest (рис. 7), имеющего средства диагностики решений, которые позволяют оценить уровень усвоения нового материала и подобрать соответствующие индивидуальные задания (рис. 8).

Выполнение индивидуальных заданий позволяет оценить результаты самостоятельной деятельности обучающегося и определить уровень освоения новой темы и сформированности самостоятельной деятельности.

Рис. 7. Пример теста в среде UzTest

Измерение эффективности обучения осуществлялось:

• на основе балльно-рейтинговой системы оценивания знаний;
• по результатам процентного соотношения правильно решённых задач к общему числу предложенных задач [9].

При этом сравнивались два класса учащихся, один из которых пользовался облачными технологиями и программой GeoGebra в обучении, а второй – нет.

Оценка эффективности методов обучения с применением перечисленных технологий происходила в сравнении с традиционными методами и заключалась в измерении результатов обучения, учитывая и затраты времени учащихся.

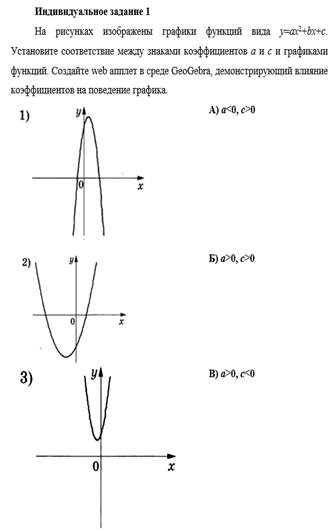
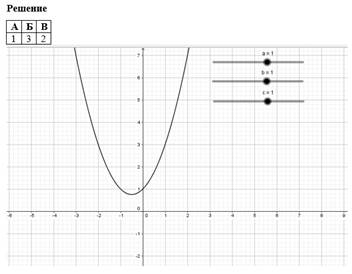
Рис. 8. Пример индивидуального задания

Результаты проведенного эксперимента показали, что применение облачных технологий и возможностей программы GeoGebra позволяет повысить объективность контроля знаний учащихся — на 20-25%, а эффективность практических занятий по математическим дисциплинам не менее чем на 30%. Успеваемость в экспериментальных классах, применяющих в обучении данные технологии, выше в среднем на 15-20%.

Таким образом, применение возможностей программы GeoGebra облегчает организацию самостоятельной деятельности обучающихся и контроль над ее результатами, а также повышает усвоение материала и наглядность построения графиков, что способствует повышению уровня образования. При этом созданный сайт и заготовки можно использовать неоднократно на протяжении всего учебного года и с различными группами учащихся, добавляя новые страницы на сайт со ссылками на файлы заданий. Следовательно, описанная методика является эффективной и мощной педагогической технологией для всего учебного процесса.

Источник: science-education.ru