Аннотация: В статье рассматривается опыт использования программного пакета GeoGebra при обучении геометрии будущих учителей математики. Рассмотрены достоинства и недостатки программы, а также механизмы её использования в учебном процессе. Приведён план специализированного модуля для освоения программы.
Ключевые слова: обучение математике, обучение геометрии, системы динамической геометрии, GeoGebra, методика обучения математике
The use of GeoGebra in teaching geometry to future mathematics teachers.
Ovsyannikova Tatiana Lvovna
Cand. Sci. (Ped.), Associate professor, Orel State University named after I.S. Turgenev (Russia, Oryol)
Abstract: This article describes the experience of using the software package GeoGebra in teaching geometry to future teachers of math, the advantages and disadvantages of the program, as well as the mechanisms of its use in the educational process, the plan of a specialized module for the development of the program GeoGebra.
Инструкция по работе в программе Geogebra
Keywords: teaching mathematics, teaching geometry, systems of dynamic geometry, GeoGebra, methods of teaching mathematics
Современные технологии обучения математике во многом определяются программным обеспечением, используемым в образовательном процессе. Действительно, сложно представить реальную практическую математическую задачу, при решении которой решающий будет лишён возможности использовать вычислительную технику и программное обеспечение.
Программное обеспечение не всегда позволяет полностью автоматизировать процесс решения математической задачи – в частности, в тех случаях, когда требуется построение математической модели, доказательство или исследование. Тем не менее, и в этом случае (в особенности – при решении геометрических задач) весьма желательна визуализация модели (в частности, построение чертежа), поскольку наглядность позволяет лучше понять проблему, упростить поиск вариантов решения (буквально «увидеть» подходы к решению). Здесь уместно вспомнить хрестоматийное высказывание К.Ф. Гаусса: «Математика – наука для глаз, а не для ушей». Во многих случаях важно не просто визуализировать модель, но проследить её поведение в динамике – при различных значениях одного или нескольких параметров, выявив и рассмотрев случаи, приводящие к неодинаковым результатам.
Программные продукты, реализующие для геометрических задач принципы наглядности и динамичности, называют системами динамической геометрии (СДГ). Использование СДГ при обучении математике позволяет:
– обеспечить высокую наглядность при изучении курсов элементарной, аналитической, дифференциальной и проективной геометрии;
– быстро и просто визуализировать аналитически заданные функции, в том числе параметрические (например, с целью локализовать области поиска решений или определить соответствующий геометрический образ).
Практически любая СДГ позволяет быстро и точно выполнять чертежи на плоскости и в трёхмерном пространстве, а также проводить исследования путём ручного или автоматического перемещения отдельных точек или изменения численных значений параметров. В сегменте СДГ существуют несколько десятков специализированных программных пакетов.
GeoGebra за 19 минут
Однако большинство из них не обладает высокой функциональностью (например, ограничены планиметрией: GeoNext, KSEG и др.), либо не поддерживают русский язык (C.a.R., Cabri, Cinderella, Dr. Geo, FreeGeo Mathematik, GeoProof, Geometria, Geometrix, Geometry Pad, GeomSpace, GEUP, Tabulae, WIRIS и т.п.), что препятствует успешному внедрению в условиях обучения в России. Для большинства программных продуктов этого сегмента уже несколько лет как прекращена дальнейшая разработка и поддержка (среди них – достаточно широко использовавшиеся в России пакеты The Geometer’s Sketchpad, (GSP), известный в России как «Живая Математика» и российский пакет «1С. Математический конструктор»). Это произошло главным образом вследствие широчайшего распространения пакета GeoGebra.
Главные достоинства пакета GeoGebra:
– простота и удобство графического интерфейса;
– возможность установки на различные операционные системы (даже на планшеты и смартфоны) и наличие онлайн-версии (впрочем, в онлайн-версии и при установке на мобильных гаджетах не поддерживается ввод команд, не представленных в графическом интерфейсе);
– наличие обширной (хотя не очень хорошо структурированной) базы примеров, открытой для добавления материалов пользователями.
В числе недостатков пакета GeoGebra можно отметить следующие:
– недостаточная документированность: система команд, не представленных в графическом интерфейсе, достаточно обширна, но не всегда интуитивно понятна, её возможности неочевидны неподготовленному пользователю программы (например, самостоятельное освоение построения параметрических кривых может вызвать у студентов некоторые трудности);
– неполная русифицированность оффлайновой программы и отсутствие русскоязычной версии официального сайта;
– отсутствие макросов и импорта формул в разметке TeX;
– отсутствие поддержки SCORM (в отличие, например, от пакета «1С. Математический конструктор»);
– непоследовательность интерфейса при переходе в 3D режим (например, теряется возможность построения ряда плоских фигур непосредственно в пространстве);
– невозможность перевода следа в линию;
– отсутствие поддержки проективных преобразований и неевклидовых геометрий.
Программа GeoGebra имеет также алгебраический модуль (существенно уступающий по функциональности системам компьютерной алгебры), табличный процессор и статистический модуль (также не очень мощный), но её геометрические возможности достаточны для большинства задач курсов элементарной, аналитической, проективной и дифференциальной геометрии.
В последние годы в России были опубликованы ряд книг и статей, рассматривающих отдельные аспекты использования пакета GeoGebra [1-6], но пока ещё отсутствуют учебные пособия, системно рассматривающие пакет как основной инструмент для выполнения построений при изучении геометрии в школе и вузе.
Отдельно можно отметить важность обучения основам работы в системах динамической геометрии будущих учителей математики. Опыт автора показывает, что учителя математики, освоившие программу GeoGebra в процессе обучения в вузе, практически всегда применяют её в своей дальнейшей педагогической деятельности, а также являются «узлами» распространения программы в общеобразовательных школах.
Основными механизмами использования пакета GeoGebra при обучении будущих учителей математики представляются следующие:
– выдача раздаточного материала, выполненного в программе GeoGebra;
– демонстрация на экране статического чертежа, выполненного в программе GeoGebra;
– демонстрация на экране динамического чертежа (с поворотом, с переходом между 2D и 3D, с изменением положения отдельных точек и т.д.);
– пошаговое построение преподавателем чертежа в программе GeoGebra в режиме реального времени (или выдача видеоролика с записью процесса построения для самостоятельного изучения);
– выдача преподавателем инструкции по построению файла в программе GeoGebra – как для освоения интерфейса программы и приёмов работы в ней, так и для самостоятельного выполнения построений и преобразований с целью доказательства теорем или рассмотрения приёмов решения задач;
– самостоятельное выполнение учащимися чертежей и визуализирующих иллюстраций при решении задач (здесь могут быть выделены несколько типовых сценариев: а) иллюстрирующие построения; б) графический эксперимент с целью поиска доказательства; в) исследование количества различных решений задачи; г) проведение численной проверки результатов вычислений, произведённых аналитически);
– проведение практикумов по работе в программе GeoGebra;
– реализация преподавателем тестовых заданий в виде апплетов программы GeoGebra (достаточно много таких заданий имеется в базе примеров на сайте проекта GeoGebra);
– поиск в базе примеров на сайте проекта GeoGebra чертежей и моделей, соответствующих рассматриваемой задаче, их анализ, а также доработка (русификация, анимация и т.п.) – такой вариант может быть уместен при выполнении достаточно сложных заданий.
Выполнение чертежа в программе GeoGebra, как правило, не является окончательным решением задачи, а лишь важной его составляющей. В некоторых случаях решение задачи может быть записано на плоскости чертежа средствами интерфейса самой программы, но для сложных задач с большим количеством последовательных действий, рассуждений и построений целесообразно выполнение дополнительного файла с решением.
В начале обучения геометрии будущих учителей имеет смысл предусмотреть отдельный модуль, посвящённый интерфейсу программы GeoGebra и повторению курса школьной геометрии – с визуализацией большинства задач при помощи динамических чертежей. Предлагаемый модуль позволит:
– актуализировать школьные знания по геометрии;
– дополнить школьные знания по элементарной геометрии; это важно в первую очередь – для тех студентов, кто изучал геометрию не на профильном, а на базовом уровне (кроме того, в российских учебниках профильного уровня материалы, дополнительные относительно базового минимума весьма существенно различаются);
– обеспечить изучение интерфейса программы и методов построений, достаточное для быстрого освоения последующих модулей, требующих динамических чертежей (аналитической геометрии, проективной геометрии и др.) независимо от того, был ли знаком данный студент на момент начала обучения с программой GeoGebra или другими системами динамической геометрии;
– научить будущего учителя самостоятельному созданию динамических чертежей для использования в профессиональной деятельности.
Например, последовательность этих занятий может быть такой:
Занятие 1. Тема: «Интерфейс и простейшие построения».
На этом занятии студенты изучают меню, особенности построения прямых, окружностей, треугольников, четырёхугольников, возможности использования ползунков, ввод текста на поле чертежа.
Занятие 2. Тема: «Задачи на построение циркулем и линейкой».
Студенты систематизируют умения и навыки, приобретённые в школе, решая, например, следующие задачи:
2.1. Постройте треугольник по трём сторонам.
2.2. Постройте окружность, касающуюся двух данных параллельных прямых и проходящую через данную точку.
2.3. Дана прямая и две точки А и В по одну сторону от неё. Найдите на прямой такую точку С, чтобы прямые АС и ВС были наклонены к прямой под равными углами.
2.4. В данный треугольник впишите квадрат так, чтобы две вершины квадрата принадлежала одной из сторон треугольника, а две других – двум другим сторонам.
2.5. Постройте равносторонний треугольник, у которого одна вершина совпадает с данной точкой, а две другие лежат на двух данных окружностях.
Занятие 3. Тема: «Анимация изображений и список команд».
Можно предложить следующие задачи.
3.1. Определите, какую траекторию будет описывать середина гипотенузы подвижного прямоугольного треугольника, сумма катетов которого равна 5.
3.2. Сделайте иллюстрацию к теореме: «Если секущая и касательная проведены из одной точки, то квадрат касательной равен произведению секущей на её внешнюю часть».
3.3. Постройте чертёж, демонстрирующий правило параллелограмма при сложении векторов.
x 2 — 7 x +10 = a x 2 — 7 x +10 = a 3.4. Найдите количество решений уравнения |х²-7|х|+10|=a в зависимости от значения параметра а.
Занятие 4. Тема: «Построения в 3D».
Для освоения построений в 3D следует предложить задачи на построение двугранных углов, сечений многогранников, вписанных и описанных многогранников. Например, следующие задачи.
4.1. Дан куб АВСDА1В1С1D1. Постройте сечение куба, проходящее через середины сторон АВ и ВС параллельно ВD1.
4.2. Постройте чертёж к задаче: «В правильной четырёхугольной пирамиде двугранный угол при ребре основания равен α. Найдите двугранный угол при боковом ребре».
4.3. Найдите площадь правильного треугольника, вписанного в окружность, являющуюся сечением сферы радиусом R плоскостью, проходящей на расстоянии a от центра сферы.
4.4. Постройте цилиндр и вписанный в него конус. Покажите, что объём конуса втрое меньше, чем цилиндра.
4.5. В правильную треугольную призму вписан шар, касающийся трёх граней и обоих оснований призмы. Найдите отношение поверхности шара к полной поверхности призмы.
Занятие 5. Итоговое занятие, предполагающее выполнение индивидуального проекта и модульной контрольной работы.
В качестве индивидуального задания будущим учителям можно предложить выполнить динамические чертежи к планиметрическим и стереометрическим задачам – например, из наборов ЕГЭ – что позволит обеспечить уникальность заданий для каждого студента: для ЕГЭ по математике (профильного уровня) образца 2018 года это задачи (3, 6, 8 и в особенности, 14 и 16).
GeoGebra является сравнительно удобным инструментарием и для других разделов математики: алгебры, анализа, математической статистики. Среди проектов, выполненных в программе GeoGebra, достаточно много посвящено теории замощения (тесселяции), имеются проекты, иллюстрирующие теорию графов, фракталы (например, множество Мандельброта) и хаотическую динамику, представляют интерес визуализации задач механики и оптики, имеющих геометрическую основу.
Навыки, полученные в программе GeoGebra, могут быть полезны и при освоении пакетов компьютерной алгебры, специализированных пакетов для численных методов и статистической обработки данных.
1. Безумова О.Л. Обучение геометрии с использованием возможностей GeoGebra. – Архангельск: КИРА, 2011, 140 с.
2. Колпакова Д.С. GeoGebra как средство визуализации решения задач на уроках геометрии в 7 классе. // Молодой учёный. 2018. №11. С. 164-167
3. Ларин С.В. Компьютерная анимация в среде GeoGebra на уроках математики: учебное пособие. – М.: Лабиринт, 2015. 192 с.
4. Овсянникова Т.Л. Использование программы GeoGebra на уроках геометрии в школе // Педагогические и психологические технологии в условиях модернизации образования. – Самара: НИЦ АЭТЕРНА, 2017. С. 166-170.
5. Садовничий Ю.В., Туркменов Р.М. Методические особенности использования интерактивной геометрической среды GeoGebra при изучении темы «решение нестандартных уравнений» // Вестник Российского университета дружбы народов. Серия: Информатизация образования. 2015. С. 78-85.
6. Танкевич Л.М., Шкляр А.Е. GeoGebra как средство решения стереометрических задач // Молодой учёный. 2018. №11. С. 53-57.
Источник: scipress.ru
Обзор и сравнительный анализ динамических сред «Живая математика», «Математический конструктор» и «GeoGebra»
Фунтиков, Р. А. Обзор и сравнительный анализ динамических сред «Живая математика», «Математический конструктор» и «GeoGebra» / Р. А. Фунтиков. — Текст : непосредственный // Молодой ученый. — 2018. — № 33 (219). — С. 8-11. — URL: https://moluch.ru/archive/219/52350/ (дата обращения: 13.06.2023).
В статье проводится краткий обзор и сравнительный анализ трёх динамических сред: Живая математика, Математический конструктор, GeoGebra; выделяются их преимущества и имеющиеся недостатки.
Ключевые слова: динамическая среда, Живая математика, Математический конструктор, GeoGebra
Перед началом использования в своей практической деятельности различных интерактивных и динамических сред учитель оказывается перед выбором этой среды. Под динамической средой будем понимать программу, позволяющую создавать динамические компьютерные чертежи и модели, исходные данные которых можно изменять, не влияя на весь алгоритм построения, а также просматривать их и работать с ними.
Сегодня наиболее популярными и распространёнными среди преподавателей программами динамической геометрии, на наш взгляд, являются Живая математика, Математический конструктор (МК) и GeoGebra. Проведём краткий обзор и сравнительный анализ каждой из этих сред, выделим их преимущества и имеющиеся недостатки.
Живая математика представляет собой среду моделирования и динамического преобразования чертежей, графиков и других объектов; позволяет решать широкий круг задач при изучении геометрии, алгебры, тригонометрии и математического анализа. Сформирована на основе программы Geometry’s Sketchpad v.4[1], переведена на русский язык и адаптирована Институтом новых технологий; может быть установлена на операционные системы (ОС): Windows, MacOS. Эта динамическая среда не является свободно распространяемым программным обеспечением (ПО): лицензия на одно рабочее место составляет 5 050 рублей[2]. Существует бесплатная демоверсия программы (устанавливается сроком на 10 дней), однако её минусом является возможность установки только на компьютер с операционной системой Windows.
Живая математика имеет полный набор возможностей для выполнения построений на плоскости, их преобразований и дальнейшей работы с ними, то есть практически полностью охватывает планиметрический материал. Предлагаемые создателями программы методические рекомендации это подтверждают — работе на плоскости посвящена большая часть предлагаемых материалов: от элементарных построений (точка, прямая, луч, отрезок, простейшие фигуры и пр.) до построения довольно сложных моделей, которые в той или иной степени можно использовать для наглядной демонстрации при доказательстве некоторых теорем из курса геометрии за 7–9 класс.
Что касается работы со стереочертежами, то возможности Живой математики довольно узки и специфичны. В среде отсутствует 3D-полотно, что, на первый взгляд, делает невозможными построение пространственных фигур и работу с ними. Тем не менее, построить объёмное тело (тело вращения и пр.), динамически изменяемое, всё-таки можно.
Однако это построение будет довольно трудоёмким и времязатратным. Опишем этот процесс. Для создания объёмного тела нужно провести дополнительные построения, которые затем можно скрыть. Подробно останавливаться на описании данного подготовительного процесса не будем, лишь покажем, какой объём подготовительной работы необходимо проделать для начала работы со стереочертежом. На рисунке 1 показаны все дополнительные построения для задания системы координат и 3D-полотна.
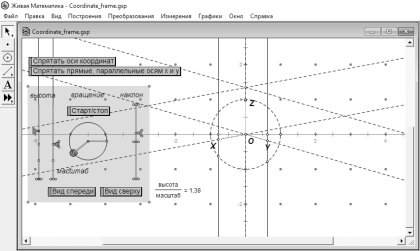
Рис. 1. 3D-полотно в среде Живая математика
Чтобы построить точку в заданной системе координат, необходимо создать числовые параметры, равные координатам данной точки, после чего применить к ним инструмент Точка по координатам. Задав точки-вершины будущего пространственного тела, нужно соединить их отрезками.
Такой подход нам кажется неуместным, поскольку привязка к системе координат и выполнение построений по координатам не всегда точны и удобны в работе. Кроме того, изменения положения тела с помощью описанных выше шкал, также является неудобным.
Математический конструктор представляет собой российскую разработку в области интерактивных динамических сред для образования. Разработчик программы — фирма 1С, которая, начиная с 1996 года, занимается созданием образовательных мультимедийных продуктов. Программа позволяет создавать интерактивные модели, объединяющие конструирование, динамическое варьирование, эксперимент, и может быть использована на всех этапах математического образования.
Среда Математический конструктор не является свободно распространяемым ПО: стоимость лицензии составляет 980 рублей[3] (одну лицензию можно использовать для установки программного обеспечения на неограниченное число устройств). Возможность установки на ОС: Windows, Linux, MacOS, IOS, Android. Также есть возможность работать в среде онлайн — на сайте производителя, однако возможности онлайн-версии продукта довольно ограничены.
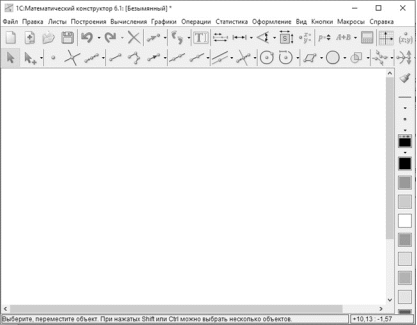
Рис. 2. Рабочее окно среды Математический конструктор
Как и предыдущая среда, МК, на наш взгляд, больше приспособлен для работы с плоскими объектами. И её возможности в этой области довольно широки — динамические геометрические построения, измерения и вычисления, функции и графики, создание заданий с автоматизированной проверкой и т. д.
В целом, интерфейс среды несложен и интуитивно понятен. Имеется необходимый набор инструментов для выполнения построений. На рисунке 2 представлено рабочее окно МК версии 6.1. В верхней части расположена панель инструментов, в правой части — элементы дизайна (позволяют выбрать цвет и стиль для построений), основную часть занимает рабочее поле (полотно).
Программа МК позволяет создавать и изменять интерактивные чертежи и модели, которые объединяют конструирование, динамическое варьирование, эксперименты, и может быть использована на всех этапах математического образования и, кроме того, в проектной деятельности учащихся.
Однако возможности этой программы для работы с пространственными объектами и стереочертежами ограничены. В ней отсутствует интерактивное 3D-полотно. Возможности работы со стереометрическими объектами пользователь может обеспечить самостоятельно.
GeoGebra[4] является динамическим программным обеспечением, визуализирующим связь между алгеброй, которая изучает буквенно-числовые выражения и равенства и неравенства этих выражений, и геометрией, которая, в свою очередь, изучает фигуры, их свойства, взаимное расположение относительно друг друга и других объектов на плоскости или в пространстве, взаимопревращения и т. д.
Разработана Маркусом Хоэнвартером (Markus Hohenwarter) австрийским математиком и профессором Университета Йоханнеса Кеплера (JKU) в Линце. Начиная с 2002 года, программа практически ежегодно завоёвывает множество образовательных наград в Европе и в США [2].
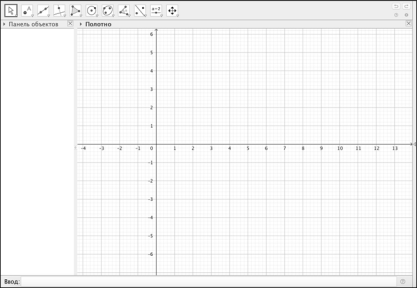
Рис. 3. Рабочее окно среды GeoGebra
Среда GeoGebra распространяется бесплатно, что позволяет беспрепятственно устанавливать её на ПК дома и в школах. Она имеет удобный и эргономичный[5] интерфейс, переведена на многие языки мира; является кроссплатформенной, то есть может быть установлена на различные операционные системы, такие как Windows, Linux, MacOS. Кроме того, есть возможность установить программу на смартфоны и планшеты, работающие под управлением операционных систем iOS и Android OS, а при необходимости — работать онлайн на сайте. На рисунке 3 представлено рабочее окно среды GeoGebra.
С одной стороны, GeoGebra представляет собой интерактивную систему геометрии. Пользователь может сделать конструкции точек, векторов, отрезков, прямых, многоугольников и конических сечений, а также функции и их динамические изменения.
С другой стороны, уравнения и координаты могут быть введены непосредственно. Таким образом, GeoGebra может работать с переменными чисел, векторов и точек, есть возможность находить производные и интегралы от функций и пр.
На основе проведённого выше анализа трёх динамических сред математического моделирования, на наш взгляд, наиболее удобной для работы учителя представляется среда GeoGebra.
- Живая математика. Сборник методических материалов. — М.: Институт Новых Технологий. — 176 с.
- Сайт среды GeoGebra [Электронный ресурс] URL: https://www.geogebra.org/about (дата обращения: 10.08.2018)
- Сайт среды Математический конструктор [Электронный ресурс] URL: http://obr.1c.ru/mathkit/ (дата обращения: 10.08.2018)
- Фунтиков Р. А. Построение эллипса, гиперболы и параболы как конических сечений и линий плоскости в динамической среде GeoGebra. Курсовая работа. М: МПГУ, 2017. — 33 с.
[1] Разработана в 1963 году фирмой Key Curriculum Press (USA).
[2] Информация взята на официальном сайте производителя математической среды Живая математика – Институт Новых Технологи и представлена по состоянию на 10 августа 2018г.
[3] Информация взята на официальном сайте производителя математической среды Математический конструктор – 1C.Образовательные программы и представлена по состоянию на 10 августа 2018г.
[4] От первых и последних букв соответственно в словах GEOmetry и alGEBRA.
[5] Эффективный в использовании, подходящий.
Основные термины (генерируются автоматически): Живая математика, Математический конструктор, среда, выполнение построений, динамическая среда, построение, рабочее окно среды, динамическое варьирование, краткий обзор, математическое образование.
Источник: moluch.ru
Для чего предназначена программа GeoGebra 6.0.450
GeoGebra – это математическое ПО, разработанное для различных образовательных учреждений. Программа написана на языке Java, поэтому для её корректной работы потребуется скачать и установить пакет от Java.
Инструменты для работы с математическими объектами и выражениями
GeoGebra предоставляет широкие возможности для работы с геометрическими фигурами, алгебраическими выражениями, таблицами, графами, статистическими данными и арифметикой. Все функции включены в один пакет для удобства. Также есть средства для работы с различными функциями, например, графиками, корнями, интегралами и т.д.
Конструирование стереометрических чертежей
В данной программе предусмотрена возможность работать в 2-х и 3-х мерном пространстве. В зависимости от выбранного пространства для работы, вы получите двумерную или трёхмерную фигуру соответственно.
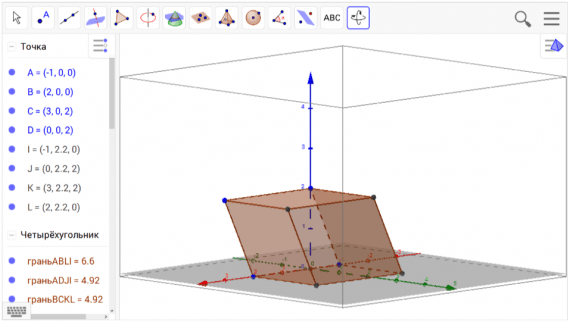
Геометрические объекты в GeoGebra формируются при помощи точек. Каждой из них можно задать те или иные параметры, провести через них линию. С готовыми фигурами тоже можно производить различные манипуляции, например, отмечать на них углы, производить измерение длины линий и сечения углов. Через них также можно проложить сечения.
Независимое построение объектов
В GeoGebra есть также функция выноса рисунка, которая позволяет делать построение объектов отдельно от основной фигуры. Например, вы можете построить какой-нибудь многогранник, а отдельно от него вынести какой-либо его компонент – угол, линию или несколько линий и углов. Благодаря этой функции можно наглядно показывать и рассказывать об особенностях какой-либо фигуры или её части.
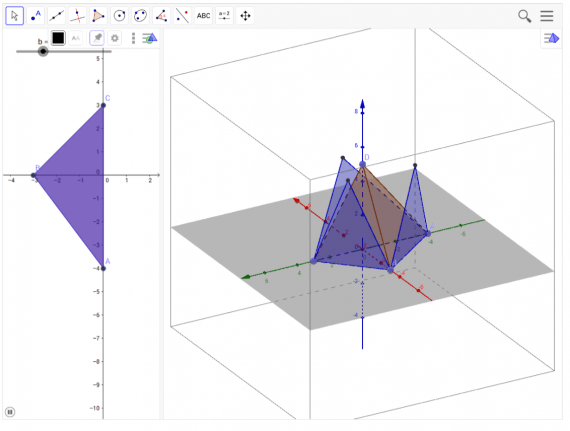
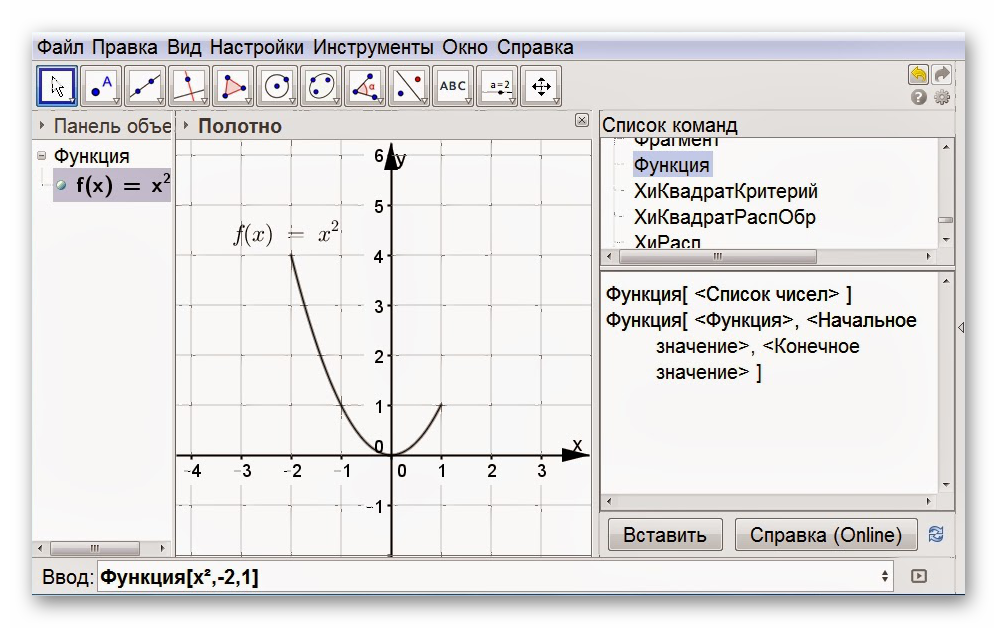
Построение графиков функции
В ПО встроен функционал, необходимый для создания различных графиков функций. Для управления ими можно использовать как специальные ползунки, так и прописывать определённые формулы. Вот простой пример:
Возобновление работы и поддержка сторонних проектов
В программе можно возобновить работу с проектом после закрытия. При необходимости можно открывать проекты, которые были скачаны с интернета и вносить туда свои корректировки.
Сообщество GeoGebra
На данный момент программа активно разрабатывается и совершенствуется. Разработчики создали специальный ресурс – GeoGebra Tube, где пользователи ПО могут делится своими предложениями, рекомендациями, а также уже готовыми проектами. Как и сама программа, все проекты, представленные на данном ресурсе, абсолютно бесплатны и их можно копировать, адаптировать под свои нужды и использовать без каких-либо ограничений в некоммерческих целях.
На данный момент на ресурсе выложено более 300 тысяч проектов и это число постоянно растёт. Единственный недостаток – это то, что большая часть проектов на английском языке. Но нужный проект можно скачать и перевести на ваш язык уже на компьютере.
Достоинства
- Удобный интерфейс, переведённый на русский язык;
- Большой функционал по работе с математическими выражениями;
- Возможность работы с графикой;
- Наличие собственного комьюнити;
- Кроссплатформенность: GeoGebra поддерживается практически всеми известными платформами – Windows, OS X, Linux. Есть приложение для Android и iOS смартфонов/планшетов. Также имеется браузерная версия, доступная в магазине приложений Google Chrome.
Недостатки
- Программа находится на стадии разработки, поэтому иногда могут встречаться баги;
- Многие проекты, которые выкладываются в сообществе, на английском языке.
GeoGebra больше подходит для создания более продвинутых графиков функции, чем те, которые изучаются в стандартном школьном курсе, поэтому школьным учителям лучше поискать более простые аналоги. Однако преподавателям ВУЗов такой вариант придётся очень кстати. Но благодаря своему функционалу программа может быть использована для показа наглядной демонстрации школьникам. Помимо различных фигур, линий, точек и формул, презентацию в данной программе можно разнообразить при помощи картинок стандартных форматов.
Источник: lumpics.ru