Стандартный язык Pascal не располагает средствами разработки и поддержки библиотек программиста (в отличие, скажем, от языка Fortran и других языков программирования высокого уровня), которые компилируются отдельно и в дальнейшем могут быть использованы как самим разработчиком, так и другими. Если программист имеет достаточно большие наработки, и те или иные подпрограммы могут быть использованы при написании новых приложений, то приходится эти подпрограммы целиком включать в новый текст.
В Turbo Pascal это ограничение преодолевается за счет, во-первых, введения внешних процедур, во-вторых, разработки и использования модулей. В настоящей публикации на примерах рассмотрим работу с теми и другими программными единицами.
Начнем с внешних подпрограмм.
Такой механизм предусматривает, что исходный текст каждой процедуры или функции хранится в отдельном файле и при необходимости с помощью специальной директивы компилятора включается в текст создаваемой программы.
Покажем это на примере задач целочисленной арифметики, где аргументы, результаты и промежуточные величины являются целыми (Integer, Word, LongInt и т.д.). Вот несколько таких задач.
Подпрограммы (процедура)
1. Дано натуральное число n. Найти сумму первой и последней цифры этого числа.
2. Дано натуральное число n. Переставить местами первую и последнюю цифры этого числа.
3. Дано натуральное число n. Дописать к нему цифру k в конец и в начало (если это возможно, т.е. результат не выйдет за диапазон допустимых значений), или сообщить о невозможности выполнения операции.
4. Найти наибольшую цифру в записи данного натурального числа.
5. Дано натуральное число n. Переставить его цифры так, чтобы образовалось максимальное число, записанное теми же цифрами.
При решении каждой из этих задач может быть использована функция, возвращающая количество цифр в записи натурального числа.
Вот возможный вариант такой функции:
Function Digits(N : LongInt) : Byte;
Var Kol : Byte;
Begin
Kol := 0;
While N <> 0 Do Begin Kol := Kol + 1; N := N Div 10 End;
Digits := Kol
End;
Сохраним этот текст в файле с расширением .inc (это расширение внешних подпрограмм в Turbo Pascal), например, digits.inc.
Еще необходима функция возведения натурального числа в натуральную степень.
Function Power(A, N : LongInt) : LongInt;
Var I, St : LongInt;
Begin
St := 1;
For I := 1 To N Do St := St * A;
Power := St
End;
Попробуем использовать функции при решении задачи номер один.
Внешние процедуры создаются и внедряются в использующие их программы аналогично функциям, и мы не будем подробно на этом останавливаться.
Далее речь пойдет о модулях: их структуре, разработке, компиляции и использовании.
Модуль — это набор ресурсов (функций, процедур, констант, переменных, типов и т.д.), разрабатываемых и хранимых независимо от использующих их программ. В отличие от внешних подпрограмм модуль может содержать достаточно большой набор процедур и функций, а также других ресурсов для разработки программ. Обычно каждый модуль содержит логически связанные между собой программные ресурсы.
Разработка ЧПУ программы и подпрограммы.
В основе идеи модульности лежат принципы структурного программирования. Существуют стандартные модули Turbo Pascal, которые обычно описываются в литературе по данному языку.
Модуль имеет следующую структуру:
После служебного слова Unit записывается имя модуля, которое (для удобства дальнейших действий) должно совпадать с именем файла, содержащего данный модуль. Поэтому (как принято в MS DOS) имя не должно содержать более 8 символов.
В разделе Interface объявляются все ресурсы, которые будут в дальнейшем доступны программисту при подключении модуля. Для подпрограмм здесь указывается лишь полный заголовок.
В разделе Implementation реализуются все подпрограммы, которые были ранее объявлены. Кроме того, здесь могут содержаться свои константы, переменные, типы, подпрограммы и т.д., которые носят вспомогательный характер и используются для написания основных подпрограмм. В отличие от ресурсов, объявленных в разделе Interface, все, что дополнительно объявляется в Implementation, уже не будет доступно при подключении модуля. При написании основных подпрограмм достаточно указать их имя (т.е. не нужно полностью переписывать весь заголовок), а затем записать тело подпрограммы.
Наконец, раздел инициализации (который часто отсутствует) содержит операторы, которые должны быть выполнены сразу же после запуска программы, использующей модуль.
Приведем пример разработки и использования модуля. Поскольку рассмотренная ниже задача достаточно элементарна, ограничимся листингом программы с подробными комментариями.
Задача. Реализовать в виде модуля набор подпрограмм для выполнения следующих операций над обыкновенными дробями вида P/Q (P — целое, Q — натуральное): 1) сложение; 2) вычитание; 3) умножение; 4) деление; 5) сокращение дроби; 6) возведение дроби в степень N (N — натуральное); 7) функции, реализующие операции отношения (равно, не равно, больше или равно, меньше или равно, больше, меньше).
Дробь представить следующим типом:
Type Frac = Record
P : Integer;
Q : 1.. High(LongInt)
End;
Используя этот модуль, решить задачи:
1. Дан массив A — массив обыкновенных дробей. Найти сумму всех дробей, ответ представить в виде несократимой дроби. Вычислить среднее арифметическое всех дробей, ответ представить в виде несократимой дроби.
2. Дан массив A — массив обыкновенных дробей. Отсортировать его в порядке возрастания.
Unit Droby;
Interface
Type
Natur = 1..High(LongInt);
Frac = Record
P : LongInt;
Q : Natur
End;
Procedure Sokr(Var A : Frac);
Procedure Summa(A, B : Frac; Var C : Frac);
Procedure Raznost(A, B : Frac; Var C : Frac);
Procedure Proizvedenie(A, B : Frac; Var C : Frac);
Procedure Chastnoe(A, B : Frac; Var C : Frac);
Procedure Stepen(A : Frac; N : Natur; Var C : Frac);
Function Menshe(A, B : Frac) : Boolean;
Function Bolshe(A, B : Frac) : Boolean;
Function Ravno(A, B : Frac) : Boolean;
Function MensheRavno(A, B : Frac) : Boolean;
Function BolsheRavno(A, B : Frac) : Boolean;
Function NeRavno(A, B : Frac) : Boolean;
Implementation
Function NodEvklid(A, B : Natur) : Natur;
Begin
While A <> B Do
If A > B Then
If A Mod B <> 0 Then A := A Mod B Else A := B
Else
If B Mod A <> 0 Then B := B Mod A Else B := A;
NodEvklid := A
End;
Procedure Sokr;
Var M, N : Natur;
Begin
If A.P <> 0 Then
Begin
If A.P < 0 Then M := Abs(A.P)
Else M := A.P;
N := NodEvklid(M, A.Q); A.P := A.P Div N; A.Q := A.Q Div N
End
End;
Procedure Summa;
Begin
C.Q := (A.Q * B.Q) Div NodEvklid(A.Q, B.Q);
C.P := A.P * C.Q Div A.Q + B.P * C.Q Div B.Q;
Sokr(C)
End;
Procedure Raznost;
Begin
C.Q := (A.Q * B.Q) Div NodEvklid(A.Q, B.Q);
C.P := A.P * C.Q Div A.Q — B.P * C.Q Div B.Q;
Sokr(C)
End;
Procedure Proizvedenie;
Begin
C.Q := A.Q * B.Q;
C.P := A.P * B.P;
Sokr(C)
End;
Procedure Chastnoe;
Begin
C.Q := A.Q * B.P;
C.P := A.P * B.Q;
Sokr(C)
End;
Procedure Stepen;
Var I : Natur;
Begin
C.Q := 1; C.P := 1; Sokr(A);
For I := 1 To N Do Proizvedenie(A, C, C)
End;
Function Menshe;
Begin Menshe := A.P * B.Q < A.Q * B.P End;
Function Bolshe;
Begin Bolshe := A.P * B.Q > A.Q * B.P End;
Function Ravno;
Begin Ravno := A.P * B.Q = A.Q * B.P End;
Function BolsheRavno;
Begin BolsheRavno := Bolshe(A, B) Or Ravno(A, B) End;
Function MensheRavno;
Begin MensheRavno := Menshe(A, B) Or Ravno(A, B) End;
Function NeRavno;
Begin NeRavno := Not Ravno(A, B) End;
Begin
End.
Дадим некоторые рекомендации по разработке модулей:
1) спроектировать модуль, т.е. выделить основные и вспомогательные подпрограммы, другие ресурсы;
2) каждую подпрограмму целесообразно отладить отдельно, после чего «вклеить» в текст модуля.
Сохраним текст разработанной программы в файле DROBY.PAS и откомпилируем наш модуль. Для этого можно воспользоваться внешним компилятором, поставляемым вместе с Turbo Pascal. Команда будет выглядеть так: TPC DROBY.PAS. Если в тексте нет синтаксических ошибок, получим файл DROBY.TPU, иначе будет соответствующее сообщение с указанием строки, содержащей ошибку. Другой способ компиляции модуля — в среде программирования Turbo Pascal выбрать в пункте меню Run подпункты Make или Build (при этом должна быть включена компиляция на диск).
Теперь можно подключить модуль к программе, где планируется его использование.
Для примера решим задачу суммирования массива дробей.
Program Sum;
Uses Droby;
Var A : Array[1..100] Of Frac;
I, N : Integer;
S : Frac;
Begin
Write(‘Введите количество элементов массива: ‘);
ReadLn(N);
S.P := 0; S.Q := 1;
For I := 1 To N Do
Begin
Write(‘Введите числитель ‘, I, ‘-й дроби: ‘); ReadLn(A[I].P);
Write(‘Введите знаменатель ‘, I, ‘-й дроби: ‘); ReadLn(A[I].Q);
Summa(A[I], S, S);
End;
WriteLn(‘Ответ: ‘, S.P, ‘/’, S.Q)
End.
Вторую задачу предлагаем решить читателю самостоятельно.
Как видно из примера, для подключения модуля используется служебное слово USES, после чего указывается имя модуля и происходит это сразу же после заголовка программы. Если необходимо подключить несколько модулей, они перечисляются через запятую.
При использовании ресурсов модуля совсем не нужно знать, как работают его подпрограммы. Достаточно обладать информацией, как выглядят их заголовки и какое действие эти подпрограммы выполняют. По такому принципу осуществляется работа со всеми стандартными модулями. Поэтому, если программист разрабатывает модули не только для личного пользования, ему необходимо сделать полное описание всех доступных при подключении ресурсов. В таком случае возможна полноценная работа с таким продуктом.
Ещё несколько слов о видимости объектов модуля. Если в программе, использующей модуль, имеются идентификаторы, совпадающие с точностью до символа с идентификаторами модуля, то они «перекрывают» соответствующие ресурсы модуля. Тем не менее, даже в такой ситуации доступ к этим ресурсам модуля может быть получен таким образом: ..
В заключение приведем набор заданий, позволяющих получить определенные навыки в разработке модулей.
I. Реализовать в виде модуля набор подпрограмм для выполнения следующих операций над комплексными числами: 1) сложение; 2) вычитание; 3) умножение; 4) деление; 5) вычисление модуля комплексного числа; 6) возведение комплексного числа в степень n (n — натуральное).
Комплексное число представить следующим типом:
Используя этот модуль, решить задачи:
1. Дан массив A — массив комплексных чисел. Получить массив C, элементами которого будут модули сумм рядом стоящих комплексных чисел.
2. Дан массив A[M] — массив комплексных чисел. Получить матрицу B[N, M], каждая строка которой получается возведением в степень, равную номеру этой строки, соответствующих элементов данного массива A.
II. Реализовать в виде модуля набор подпрограмм для выполнения следующих операций с квадратными матрицами: 1) сложение двух матриц; 2) умножение одной матрицы на другую; 3) нахождение транспонированной матрицы; 4) вычисление определителя матрицы.
Матрицу описать следующим образом:
Const NMax = 10;
Type Matrica = Array [1..NMax, 1..Nmax] Of Real;
Используя этот модуль, решить следующие задачи:
1. Решить систему линейных уравнений N-го порядка (2N<=10) методом Крамера.
2. Задан массив величин типа Matrica. Отсортировать этот массив в порядке возрастания значений определителей матриц.
III. Реализовать в виде модуля набор подпрограмм для выполнения следующих операций над векторами на плоскости: 1) сложение; 2) вычитание; 3) скалярное умножение векторов; 4) умножение вектора на число; 5) длина вектора.
Вектор представить следующим типом:
Type Vector = Record X, Y : Real End;
Используя этот модуль, решить задачи:
1. Дан массив A — массив векторов. Отсортировать его в порядке убывания длин векторов.
2. С помощью датчика случайных чисел сгенерировать 2N целых чисел. N пар этих чисел задают N точек координатной плоскости. Вывести номера тройки точек, которые являются координатами вершин треугольника с наибольшим углом.
IV. Реализовать в виде модуля набор подпрограмм для выполнения следующих операций над натуральными числами в P-ичной системе счисления (2P<=9): 1) сложение; 2) вычитание; 3) умножение; 4) деление; 5) перевод из десятичной системы счисления в P-ичную; 6) перевод из P-ичной системы счисления в десятичную; 7) логическая функция проверки правильности записи числа в P-ичной системе счисления; 8) функции, реализующие операции отношения (равно, не равно, больше или равно, меньше или равно, больше, меньше).
P-ичное число представить следующим типом:
Type Chislo = Array [1..64] Of 0..8;
Используя этот модуль, решить задачи:
1. Возвести число в степень (основание и показатель степени записаны в P-ичной системе счисления). Ответ выдать в P-ичной и десятичной системах счисления.
2. Дан массив A — массив чисел, записанных в P-ичной системе счисления. Отсортировать его в порядке убывания. Ответ выдать в P-ичной и десятичной системах счисления.
V. Реализовать в виде модуля набор подпрограмм для выполнения следующих операций над натуральными числами в шестнадцатеричной системе счисления: 1) сложение; 2) вычитание; 3) умножение; 4) деление; 5) перевод из двоичной системы счисления в шестнадцатеричную; 6) перевод из шестнадцатеричной системы счисления в десятичную; 7) функция проверки правильности записи числа в шестнадцатеричной системе счисления; 8) функции, реализующие операции отношения (равно, не равно, больше или равно, меньше или равно, больше, меньше).
Используя этот модуль, решить задачи:
1. Возвести число в степень (основание и показатель степени записаны в шестнадцатеричной системе счисления). Ответ выдать в шестнадцатеричной и десятичной системах счисления.
2. Дан массив A — массив чисел, записанных в шестнадцатеричной системе счисления. Отсортировать его в порядке убывания. Ответ выдать в шестнадцатеричной и десятичной системах счисления.
VI. Определим граф как набор точек, некоторые из которых соединены отрезками, подграф — граф, подмножество данного графа. Реализовать в виде модуля набор подпрограмм, определяющих: 1) число точек в графе; 2) число отрезков в графе; 3) число изолированных подграфов в графе (подграфов, не соединенных отрезками); 4) диаметр графа — длину максимальной незамкнутой линии в графе (длина каждого звена — единица); 5) граф — объединение двух графов; 6) подграф — пересечение двух графов; 7) подграф — дополнение данного графа до полного (графа с тем же количеством вершин, что и в заданном, и с линиями между любыми двумя вершинами); 8) число отрезков, выходящих из каждой вершины графа; 9) при запуске должны инициализироваться переменные: Full_Graph — полный граф с числом вершин NumberOfVertix, Null_Graph — граф без отрезков с числом вершин NumberOfVertix.
Граф представить как объект
Const NumberOfVertix = 50;
Type Graph = Array[1..NumberOfVertix, 1..NumberOfVertix] Of Boolean;
Используя модуль, решить задачу: найти все правильные графы из N вершин (граф правилен, если из всех вершин выходит равное количество отрезков).
VII. Реализовать в виде модуля набор подпрограмм для работы с длинными целыми числами (числами, выходящими за диапазон допустимых значений любого целого типа): 1) сложение; 2) вычитание; 3) умножение; 4) нахождение частного и остатка от деления одного числа на другое; 5) функции, реализующие операции отношения (равно, не равно, больше или равно, меньше или равно, больше, меньше).
Длинное число представить следующим типом:
Type Tsifra = 0..9; Chislo = Array [1..1000] Of Tsifra;
Используя этот модуль, решить задачи:
1. Возвести число в степень (основание и показатель степени — длинные числа).
2. Дан массив длинных чисел. Упорядочить этот массив в порядке убывания.
VIII. Реализовать в виде модуля набор подпрограмм для выполнения операций с многочленами от одной переменной (первый многочлен степени m, второй — степени n): 1) сложение; 2) вычитание; 3) умножение; 4) деление с остатком; 5) операции отношения (равно, не равно); 6) возведение в натуральную степень k одного из многочленов; 7) вычисление производной от многочлена; 8) вычисление значения в точке x0.
Многочлен представить следующим типом:
Type Mnogochlen = Array [1..500] Of Integer;
Используя этот модуль, решить задачи:
1. Найти наибольший общий делитель многочленов P(x) и Q(x).
IX*. Реализовать в виде модуля набор подпрограмм для работы с длинными действительными числами (числами, выходящими за диапазон допустимых значений любого действительных типа или не представленных в памяти ЭВМ): 1) сложение; 2) вычитание; 3) умножение; 4) нахождение частного от деления одного числа на другое с заданным количеством знаков после запятой; 5) функции, реализующие операции отношения (равно, не равно, больше или равно, меньше или равно, больше, меньше); 6) тригонометрические функции, где аргументом и значениями являются длинные действительные числа (указание: использовать разложение соответствующей функции в ряд).
Длинное действительное число представить следующим типом:
Type Tsifra = 0..9; Chislo = Array [1..1000] Of Tsifra;
LongReal = Record
Znak : 0..1;
Ts, Dr : Chislo
End;
Используя этот модуль, решить задачи:
1. Возвести число в степень (основание — длинное действительное, показатель степени — длинное целое число).
2. Дан массив длинных действительных чисел. Упорядочить этот массив в порядке возрастания.
Источник: www.examen.ru
Разработка алгоритмов различной структуры с помощью программных средств
Практика программирования показала необходимость научно обоснованной методологии разработки и документирования алгоритмов и программ. Алгоритм может быть предназначен для выполнения его человеком или автоматическим устройством. Создание алгоритма, пусть даже самого простого, — процесс творческий. Он доступен исключительно живым существам. Эта методология должна касаться анализа исходной задачи, разделения ее на достаточно самостоятельные части и программирования этих частей по возможности независимо друг от друга.
Введение.
Разработка алгоритмов.
Понятие алгоритма и его свойства.
Виды представления алгоритмов.
Линейные алгоритмы.
Ветвящиеся алгоритмы.
Циклические алгоритмы.
Используемые программные средства.
Pascal.
Excel.
Система MathCad.
Решение задач.
Задание № 1.
Задание № 2.
Задание № 3.
Задание № 4.
Задание № 5.
Задание № 6.
Задание № 7.
Задание № 8.
Задание № 9.
Задание № 10.
Задание № 11.
Задание № 12.
Заключение.
Список литературы.
Работа содержит 1 файл
Например, алгоритмами являются правила выполнения арифметических операций в позиционной системе счисления, описание передвижения человека в городе от одной точки до другой, рецепт приготовления кулинарного блюда или лекарства, алгоритм деления отрезка прямой или угла пополам и т.д.
Алгоритмами не являются процесс рисования картины художником, процесс решения задачи, процесс воспитания человека и т.д.
Алгоритмы можно представить в разных формах. Различают:
- Словесноепредставление алгоритмов.
Словесный способ не имеет широкого распространения по следующим причинам: такие описания строго не формализуемы; страдают многословностью записей; допускают неоднозначность толкования отдельных предписаний.
- Представление алгоритма в виде программы на алгоритмическом языке.
В дальнейшем для записи алгоритмов будем использовать алгоритмический язык Pascal.
- Представление алгоритма в виде блок-схемы.
Это способ описания представляет собой изображение логико- математической структуры алгоритма, при которой все этапы процесса обработки данных представляются с помощью определенного набора геометрических фигур (блоков), имеющих строго определенную конфигурацию в соответствии с характером выполняемых действий (см. таблицу 1).
Таблица 1. Основные графические обозначения блоков программ.
| Наименование | Обозначение | Функции |
| Процесс | Выполнение операции или группы операций, в результате которых изменяется значение, форма представления или расположение данных | |
| Вход-выход | Преобразование данных в форму, пригодную для обработки (ввод) или отображения результатов обработки (вывод) | |
| Решение | Выбор направления выполнения алгоритма в зависимости от некоторых перемененных условий | |
| Предопределенный процесс | Использование ранее созданных и отдельно написанных программ (подпрограмм) | |
| Документ | Вывод данных на бумажный носитель | |
| Магнитный диск | Ввод-вывод данных, носителем которых служит магнитный диск | |
| Пуск-останов | Начало, конец, прерывание процесса обработки данных | |
| Соединитель | Указание связи между прерванными линиями, соединяющими блоки | |
| Межстраничный соединитель | Указание связи между прерванными линиями, соединяющими блоки, расположенные на разных листах | |
| Комментарий | Связи между элементом схемы и пояснениями |
Представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов.
Он занимает промежуточное место между естественным и формальным языками.
С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.
В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя. Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова , смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются. Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций.
Примером псевдокода является школьный алгоритмический язык в русской нотации ( школьный АЯ ), описанный в учебнике А.Г. Кушниренко и др. «Основы информатики и вычислительной техники», 1991.
Простейшим способом построения новых алгоритмов является последовательное исполнение команд исполнителя и других алгоритмов, написанных для данного исполнителя ранее. Такие алгоритмы называются линейными. Запись команд для исполнителя осуществляется на алгоритмических языках операторами. Для записи линейных алгоритмов используются операторы ввода, вывода, присваивания, оператор процедуры.
Оператор ввода предназначен для приема (получения) от человека исходных данных и размещения их в памяти компьютера. Форма записи этого оператора в Pascal может быть одной из трех:
— read(список скалярных переменных);
— readln(список скалярных переменных);
При выполнении этого оператора компьютер остановится и будет ждать, когда пользователь (человек, работающий за компьютером) введет столько констант, сколько переменных указано в списке оператора. Вводимые константы разделяются одним или несколькими пробелами и заносятся в специальный буфер — буфер клавиатуры. Признаком окончания ввода является нажатие клавиши Enter.
Код этой клавиши, как и введенные константы, заносится в буфер клавиатуры. После нажатия клавиши Enter компьютер продолжит исполнение оператора ввода. Первая константа пересылается в первую переменную списка, вторая — во вторую и т.д. Если пользователь ввел меньше констант, чем переменных в списке, то ожидание окончания ввода будет продолжаться.
По окончании ввода в буфере клавиатуры останется признак нажатия клавиши Enter. Чтобы его убрать из буфера, в операторе используется суффикс ln.
Оператор ввода readln заставит компьютер ожидать до тех пор, пока в буфере клавиатуры не появится признак нажатия клавиши Enter.
Оператор вывода предназначен для передачи данных из оперативной памяти компьютера и преобразования их в форму, удобную для восприятия человеком. Его можно записать в одной из трех форм:
— write(список выражений);
— writeln(список выражений);
Если сравнивать этот оператор с оператором ввода, то можно заметить много общего в их устройстве. Прежде всего, и тот и другой операторы существуют в трех формах, начинаются со служебного символа, который может иметь суффикс ln, далее может следовать список объектов, в котором объекты перечисляются через запятую. В операторе ввода объектами могут быть только переменные, тогда как в операторе вывода объектом может быть выражение, что является общим случаем по сравнению с переменной.
При выполнении оператора вывода сначала вычисляются значения выражений из списка, а затем выражения выводятся в порядке их следования в списке на экран с того места, где находился курсор. По окончании вывода курсор остается в следующей свободной позиции. Если в записи оператора присутствует суффикс ln, то по окончании вывода курсор автоматически переводится в первую позицию следующей строки.
Для выражений в списке оператора вывода можно указать размерность вывода. Для данных целого типа размерность задается в виде: данное:число, где число указывает количество позиций, которое должно занять значение на экране. Если количество позиций окажется меньше, чем нужно для вывода, то компьютер автоматически добавит недостающие позиции.
Для данных типа real размерность задается в виде: данное:число1:число2, где число 1 задает общее количество позиций для представления значения данного, а число 2 указывает количество позиций в дробной части. Если ширина поля не указана, то она определяется компьютером. Оператор присваивания предназначен для изменения содержимого оперативной памяти. Старое значение при этом стирается и записывается новое. На Паскале этот оператор записывается так: переменная:=выражение.
Исполняется оператор в два этапа:
1) вычисляется значение выражения, записанное справа;
2) вычисленное значение пересылается в переменную слева.
Ветвящимся называется алгоритм, в котором в зависимости от выполнения некоторого условия выполняется та или иная группа действий. Условие задается логическим выражением и принимает два значения: false (ложь) или true (истина). В Pascal ветвящиеся алгоритмы записываются с помощью условных операторов. Полный условный оператор записывается так:
then оператор1
else оператор2.
Выполняется данный оператор следующим образом: если условие принимает значение «истина», то управление передается на оператор1, если же нет, то на оператор2.
Компилятор Паскаля всегда выбирает первый из приведенных вариантов – каждому else соответствует ближайший предшествующий if. Если требуется реализация второго варианта, можно использовать операторные скобки begin…end. В общем случае, чтобы четко определить, что чему подчинено, используйте begin…end аналогично круглым скобкам в арифметических выражениях.
Структура ветвления обеспечивает в зависимости от результата проверки условия (да или нет) выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.
Структура ветвление существует в четырех основных вариантах (см. таблицу 2).
Таблица 2. Виды структуры ветвления.
то действия
то действия 1
иначе действия 2
при условие 1: действия 1
при условие 2: действия 2
при условие N: действия N
при условие 1: действия 1
при условие 2: действия 2
при условие N: действия N
иначе действия N+1
Циклическим называется такой алгоритм, в котором некоторая группа действий повторяется неоднократно. Группа действий, повторяемая в цикле, называется его телом. Однократное выполнение тела цикла называется шагом.
Чтобы алгоритм не зациклился (не стал бесконечным), циклом надо управлять. Для этого используется специальная величина — параметр цикла.
Параметр (переменная) цикла — это такая величина, которая изменяется от шага к шагу и по значению которой определяется, продолжать исполнение цикла или его закончить.
Источник: www.stud24.ru
Научиться создавать программы, преобразовывать в подпрограммы и научиться использовать подпрограммы в других приложениях.
2.2.1. Использование CASE-структуры в создаваемых приложениях.
2.2.2. Применение цикла типа For-Do в своих программах.
2.2.3. Изменение свойства графического элемента управления «Кнопка».
2.2.4. Обрабатывание нажатия кнопок.
2.2.5. Использование редактора формул для написания кода программы.
2.2.6. Создание подпрограммы и сохранение их в виде отдельного виртуального инструмента.
2.2.7. Оформление иконки полученной подпрограммы и установление связи иконки с используемыми в подпрограмме параметрами.
2.2.8. Изменение свойства подпрограммы и сохранение их в виде отдельных файлов или в составе библиотеки.
2.2.9. Использование созданную подпрограмму в других приложениях.
Основные теоретические сведения
В LabVIEW реализовано шесть вариантов реакций на нажатие кнопки: Switch When Pressed (Реагирует на нажатие); Switch When Released (Реагирует на отжатие); Switch Until Released (Реагирует на нажатие и отжатие); Latch When Pressed (Изменяет управляемое значение при нажатии и обеспечивает автовозврат не раньше, чем произойдет чтение в программе); Latch When Released (Изменяет управляемое значение только после отпускания кнопки и обеспечивает автовозврат); Latch Until Released (Изменяет управляемое значение при нажатии и обеспечивает автовозврат не раньше, чем произойдет чтение в программе или будет отпущена кнопка). LabVIEW – это иконизированное представление какого-либо алгоритма со своим графическим интерфейсом или без него. Создание подпрограммы по своей сути не будет отличаться от написания программ, составленных ранее.
Порядок выполнения работы
2.4.1 Создадим элементарную программу, которая позволит, в зависимости от положения тумблера, получать различный результат вычислений. Если тумблер находится в выключенном состоянии, то значение входного параметра будет умножаться на 10, а в противном случае — меняться не будет.
Приступим к реализации задачи. Создадим новый VI.Формируем на панели графический интерфейс (рис. 23)

Рисунок 23 – Графический интерфейс
Элементы графического интерфейса, определяющие входные параметры размещаем слева, а выходные, т.е. результат — справа.
Теперь реализуем условный алгоритм. Переходим в окно редактирования диаграмм. Устанавливаем в это окно CASE структуру, которая находится в Functions >> Structures >> Case. Изменяем ее размеры. Заметим, что по умолчанию состояние определено как True (истина).
Соединяем элементы диаграммы как показано на рисунке 24.
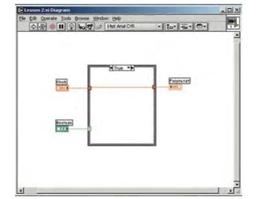
Рисунок 24 – Последовательность соединения элементов диаграммы
Переключаем режим CASE-структуры на False (ложь). Для этого необходимо подвести указатель мыши к одной из стрелок структуры (левая/правая) и нажать левую кнопку. Состояние изменится. Согласно заданию реализуем алгоритм умножения значения входного параметра на 10.
Для этого необходимо установить необходимые компоненты в окно редактирования диаграмм и соединить их (рис. 25).
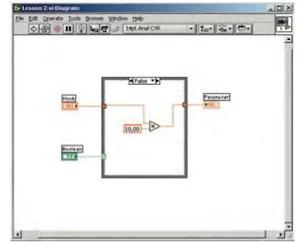
Рисунок 25 – Окно редактирования диаграмм
Переходим на интерфейсную панель и запускаем программу на выполнение в циклическом режиме.
2.4.2 Напишем программу, которая генерирует последовательность случайных чисел и выводит их в виде графика. Кроме того, по однократному нажатию на кнопку должна производиться запись выборки чисел. Графический интерфейс должен включать, как необходимый и достаточный минимум, три графических объекта: окно отображения графика, кнопку записи данных на диск и кнопку останова выполнения программы. В результате, должна визуально получиться похожая «лицевая» часть программы (рис. 26):
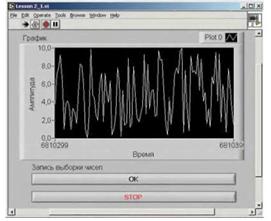
Рисунок 26 – Пример «лицевой» части программы
В процессе выполнения задания воспользуемся дополнительными функциями, связанными с нажатием на интерфейсные кнопки/переключатели. Речь идет о реакции (поведении) кнопки на нажатие, т.е. возвращается ли кнопка после нажатия в исходное состояние или же остается в нажатом состоянии и т.д.
В нашей программе нужно установить для обеих кнопок такие опции реакции на нажатие, чтобы кнопки возвращались в предыдущее положение. Если этого не сделать для первой кнопки (записи данных на диск), то после нажатия на кнопку во время работы программы, будет циклически «выскакивать» меню записи файла на диск, т.е. в результате получится, что осуществить остановку программы будет невозможно. Для реализации этого небольшого нововведения необходимо подвести указатель мыши к одной из кнопок и нажать правую кнопку мыши. В выпадающем меню выбрать Mechanical Action, а в нем Latch When Released
Такую же операцию можно проделать и для кнопки остановки.
Теперь остается реализовать алгоритм программы. В результате получим следующую диаграмму (рис. 27):
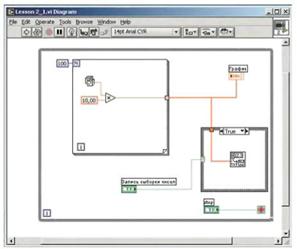
Рисунок 27 – Диаграмма, полученная при реализации алгоритма программы
Из приведенных состояний программы видно, что генерируются выборки случайных чисел (по 100 значений в каждой), результат выводится в виде графика, а запись осуществляется посредством нажатия на кнопку. Следует отметить, что реализация CASE-структуры выполнена так, что при нажатии (т.е. когда условие «Тrue»), вызывается диалоговое меню записи файла на диск и осуществляется запись данных. Если же условие «False», то запись не происходит.
В некоторых ситуациях обычная синтаксическая запись выражения гораздо более удобна и выглядит нагляднее, чем эквивалентная графическая диаграмма. Особенно это актуально при написании математических выражений, вычисляемых по определенной формуле. Для этой цели в LabVIEW существует механизм Formula Node (Формульный узел или Редактор Формул). Formula Node относится к еще одной разновидности структур. Поэтому он находится в (Functions) >> Structures >> Formula Node.
2.4.3 Напишем новую программу, которая будет строить графическую зависимость амплитуды от текущего значения переменной цикла. Редактор формул должен будет реализовывать следующую зависимость:
Результат = Амплитуда * SIN (Константа * Текущее значение переменной цикла)
Установим Formula Node в окно редактирования диаграмм. Для того чтобы можно было использовать этот «черный квадрат», нужно подвести указатель мыши к левой стороне прямоугольника и нажать правую кнопку мыши.
В выпадающем меню выбрать опцию Add Input, которая добавляет входной параметр узла. Ввести имя входного параметра «Амплитуда» (только латинские символы), например, Ampl.
Аналогично добавляем еще один входной параметр, соответствующий переменной цикла. Называем его i. Для добавления выходного параметра необходимо нажать правой клавишей мыши на правой стороне рамки редактора формул, выбрать опцию Add Output и ввести имя выходного параметра у. Чтобы ввести формулу, необходимо сначала переключиться в режим редактирования текста: Tools >> Edit Text, затем установить курсор внутрь окна редактора формул и ввести ее. Для размещения формулы в середине окна редактора формул нужно перед первым символом нажать несколько раз Enter
Создаем диаграмму, т.е. устанавливаем необходимые компоненты и делаем соответствующие связи.
Графический интерфейс составьте по своему усмотрению. Запускаем программу на исполнение.
2.4.3 Усвоив принципы использования редактора формул, составим программу генерации последовательности случайных чисел. Синтаксические конструкции, которые используется в таких блоках, позаимствованы из языка Си, что упрощает их понимание и использование.
Из приведенной ниже графической диаграммы видно, что синтаксис записи редактора формул очень похож на код языка Си (рис. 28). Во фрагменте программы использованы комментарии, объявления переменной и массива, а также тело самой программы.
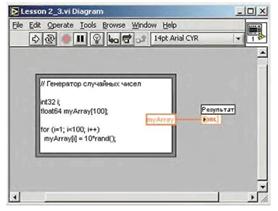
Рисунок 28 – Синтаксис записи редактора формул
Параметрами редактора формул могут быть не только переменные или константы, но и другие типы данных, например, как в данном случае — массив. Написав такую программу и запустив ее на выполнение, получим сгенерированную последовательность из 100 случайных чисел
2.4.4 Составим подпрограмму (графическую диаграмму и интерфейс) как показано на приведенных ниже рисунках 29 и 30:

Рисунок 29 – Графическая диаграмма
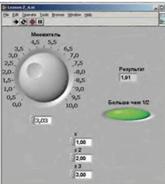
Рисунок 30 – Графический интерфейс
Входными параметрами в примере являются четыре действительных числа, три из которых — основные параметры, а четвертый — множитель. Каждое входное значение умножается на множитель, полученные значения усредняются, т.е. суммируются и делятся на три. Дальше осуществляется элементарная проверка. Если получаемое значение больше чем 0.5, тогда «зажигается» лампочка индикатора (значение «true»).
2.4.5 Теперь создадим уникальную графическую иконку для подпрограммы. Для реализации этого необходимо подвести указатель мыши к установленной по умолчанию иконке в правом верхнем углу интерфейсной панели и сделать двойной щелчок левой клавишей мыши. Появится графический редактор иконок со стандартным набором инструментов для создания желаемого образа. Нажав ОК, увидим, что иконка в правом верхнем углу изменится на желаемую (рис. 31).

Рисунок 31 – Вид измененной иконки
Установим соответствие между функциональными элементами программы и выводами иконки. Для этого необходимо подвести указатель мыши к изображению иконки в правом верхнем углу интерфейсной панели, и нажать правую клавишу мыши. В выпадающем меню следует выбрать опцию Show Connector.
После этого действия иконка изменится и появится несколько, в данном случае шесть, клеток (клемм), которые и будут соответствовать шести параметрам подпрограммы (4-входных и 2-выходных). Чтобы установить соответствие параметров подпрограммы выводам коннекторов, необходимо произвести следующие операции.
Подвести указатель мыши в виде соединительной катушки к первому контакту на иконке коннектора и нажать левую клавишу мыши. Активная клеточка подсветится. Далее следует подвести указатель к первому параметру подпрограммы, а именно «х», и нажать левую клавишу мыши. Цвет клеточки изменится.
Для остальных параметров следует проделать аналогичную операцию, последовательно устанавливая соответствия между графическими элементами и клеммами иконки коннектора. Следует отметить, что цвет клеммы зависит от типа данных элемента. Так, если элемент принимает значения действительного типа, то клемма будет оранжевая, если же это булевый тип — то зеленая. Т.е., каким цветом отображаются эти элементы в окне редактирования диаграмм, такого же цвета и клеммы.
Установив все необходимые соответствия, можно сохранить подпрограмму. Особенностью подпрограмм LabVIEW является то, что они могут функционировать как независимые автономные приложения, так и быть частью основной программы.
Следующим шагом будет сохранение нашей подпрограммы в библиотеке. Библиотека LabVIEW представляет собой составной файл, в котором находятся несколько различных виртуальных инструментов (как правило, объединенных тематически).
Выбрать в меню File опцию Save As… В появившемся меню нужно выбрать желаемую директорию и нажать кнопку New VI Library. Далее следует ввести имя библиотеки, например «ourlib». Потом следует ввести имя самой подпрограммы, например «subsin».
2.4.6 Теперь перейдем к созданию главной программы, в которой будет использоваться написанная подпрограмма. Есть несколько способов вызова иконки подпрограммы в окно редактирования диаграмм:
Первый способ заключается в простом перетягивании иконки, которая находится в правом верхнем углу открытого окна подпрограммы в окно редактирования диаграмм главной программы. Нажав левую клавишу мыши на этой иконке, и удерживая ее в нажатом состоянии, перетащим в окно редактирования диаграмм.
Второй способ — перейдя в окно редактирования диаграмм, в функциональной (Functions) панели необходимо выбрать Select a VI.В появившемся диалоговом окне выбираем созданную ранее библиотеку ourlib. В появившемся окне необходимо выбрать subsinи установить иконку в произвольное место окна редактирования диаграмм
Составьте графическую диаграмму, как показано на рисунке 32.
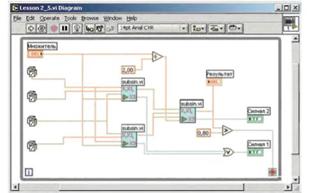
Рисунок 32 – Графическая диаграмма
Суть программы состоит в том, что на входы подпрограмм подаются случайные числа от четырех источников. Далее они обрабатываются и анализируются в соответствии с диаграммой. Результат выводится в виде графической зависимости. Условием завершения программы является превышение выходным параметром значения 0,8.
Задания
2.5.1 Создать свою подпрограмму с расшифровкой и необходимостью использования.
2.5.2 Пояснить алгоритм работы последней программы.
2.5.3 Изменить и зафиксировать значения параметров, когда отсутствуют оба сигнала, передать значение в Excel.
2.5.4 Изменить и зафиксировать значения параметров, когда отсутствует Сигнал1, передать значение в Excel.
2.5.5 Изменить и зафиксировать значения параметров, когда отсутствует Сигнал2, передать значение в Excel.
2.5.6 Изменить и зафиксировать значения параметров, когда присутствуют оба сигнала, передать значение в Excel
2.5.7 Задать отрицательные значения параметров и проверить может ли работать программа, будут ли присутствовать сигналы, ответ пояснить.
Контрольные вопросы
2.6.1 Перечислите основные варианты реакций на нажатие кнопки в среде Lab VIEW. Опишите реакции.
2.6.2 Для чего в Lab VIEW необходимы дополнительные функции связанные
с нажатием кнопки?
2.6.3 Какое действие происходит при реализации CASE-структуры, если условием является «True»?
2.6.4 Какое действие происходит при реализации CASE-структуры, если условием является «False»?
2.6.5 Каким образом устанавливаются соответствия между функциональными элементами программы и выводами иконок?
2.6.6 Какую функцию выполняет опция «Show Connector»?
2.6.7 Отчего зависит цвет клеммы? Что означают данные цвета?
2.6.8 Что собой представляет библиотека Lab VIEW. назовите её основные функции.
2.6.9 Назовите способы вызова иконок подпрограмм в окно редактирования диаграмм. Какой из способов является универсальным и почему?
2.7 Содержание отчета
2.7.1 Цель работы.
2.7.2 Описание экспериментов.
2.7.3 Выполненные задания.
2.7.4 Ответы на контрольные вопросы.
2.7.5 Выводы по работе.
Список используемой литературы
2.8.1 Блюм Питер. LabVIEW. Стиль программирования.- М: ДМК Пресс, 2008.- 400 с.
2.8.2 Федосов В. П., Нестеренко А. К. Цифровая обработка сигналов в LabVIEW. – М: ДМК Пресс, 2007. – 256 с.
2.8.3. Джеффри Тревис LabVIEW для всех.М.: ДМК пресс, ПриборКомплект, 2005. – 544 с.
2.8.4. Визильтер Ю. В., Желтов С. Ю., Князь В. А., Ходарев А. Н. Обработка и анализ цифровых изображений с примерами на LabVIEW и IMAQ Vision. М.: ДМК пресс, ПриборКомплект, 2008. – 464 с.
2.8.5. Суранов А. Я. LabVIEW 8.20 Справочник по функциям. М.: ДМК пресс, ПриборКомплект, 2007. – 536 с.
2.8.6. Бутырин П. А., Васьковская Т. А., Каратаев В. В., Материнкин С. В.
Автоматизация физических исследований и эксперимента: компьютерные измерения и виртуальные приборы на основе LabVIEW 7. М.: ДМК пресс, ПриборКомплект, 2007. – 264 с.
2.8.7. Кучерявский С.В., Суранов А.Я. Основы сетевых технологий. Создание сетевых приложений в среде LabVIEW. Изд-во Алтайского ун-та , 2005. – 49 с.
Лабораторная работа №3
Дата добавления: 2018-05-12 ; просмотров: 428 ; Мы поможем в написании вашей работы!
Источник: studopedia.net