чертежей. Особенно поучителен сам процесс создания соответствующего рисунка.
Применение программ ы « GeoGebra » на различных этапах урока математики
Наименование организации: государственное общеобразовательное учреждение Самарской области основная общеобразовательная школа посёлка Степняки муниципального района Приволжский Самарской области (ГБОУ ООШ пос. Степняки)
Должность автора: учитель математики и информатики
Компьютерные технологии завоевывают все больше доверия и симпатии школьников и учителей математики. Во время дистанционных курсов я познакомилась с компьютерной п рограмм ой « GeoGebra » , которая з а меняет все математические программы, является одной из сам ых популярн ых в мире. У диви тельна простот а и доступност ь этой программы, в ней не надо мучи ться при наборе формул функций, при построении геометрических фигур и т . д .
Эта программа создана в 20 0 1 году и очень бурно развивается. Программа написана Маркусом Хохенвартером на языке Java , работает на большом числе операционных систем. Переведена на 39 языков и в настоящее время активно разрабатывается. Переведена на русский язык в 2013 году. Эта программа — пакет инструментов «на все случаи жизни».
GeoGebra учителю математики. Занятие1.
При работе с этой программой в результате компьютерного моделирования многие математические понятия и теоремы становятся для учащихся «видимыми» и «осязаемыми».
О программе Гео Гебра
GeoGebra позволяет визуализировать математику, проводить эксперименты и исследования при решении математических задач не только геометрического характера. GeoG ebra позволяет создавать на экране компьютера чертежи, которые можно использовать на разных стадиях изучения учебного материала, от живых плакатов до исследовательских чертежей. Особенно поучителен сам процесс создания соответствующего рисунка.
Интерфейс программы GeoGebra ( ГеоГебра ) напоминает классную доску, на которой можно рисовать графики, создавать геометрические фигуры и т.п. В окне программы будет наглядно отображены производимые изменения: если вы измените уравнение, кривая перестроится, изменится масштаб или ее положение в пространстве, уравнение, написанное рядом с кривой, автоматически будет скорректировано, согласно новым значениям.
Программу GeoGebra широко используют в мире миллионы пользователей для обучения алгебре и геометрии. Процесс обучения нагляден благодаря визуальной форме использования приложения.
Возможности программы по математике не ограничиваются только построением графиков. Программу GeoGebra можно будет использовать для интерактивных чертежей при решении геометрических задач. Программа GeoGebra обладает мощными и функциональными возможностями, которые позволяет наглядно и просто обучаться математике. Приложение включает в себя геометрию, алгебру, есть возможность совершать арифметические операции, создавать таблицы, графики, возможна работа со статистикой, работа с функциями, поддерживается создание анимации и т.д.
В программе GeoGebra можно будет создавать различные 2D и 3D фигуры, интерактивные ролики, которые затем можно будет размещать в интернете. У программы богатые возможности работы с функциями за счёт команд встроенного языка (который, кстати, позволяет управлять и геометрическими построениями) .
Применение программы GeoGebra на уроках математики
Интерфейс программы довольно прост и напоминает графический редактор.
1. Полоса меню. Из меню вы можете изменить настройки программы.
2. Панель инструментов. Здесь находятся инструменты для создания объектов. После щелчка по треугольнику в правом нижнем углу кнопки, будут открыты дополнительные инструменты. Операции, доступные в панели инструментов, можно производить с помощью строки ввода.
3. Панель объектов. В Панели объектов отображаются введенные переменные и функции. Вместо имен переменных здесь отображаются их значения. Для того , чтобы увидеть формулу в символьном виде, нужно будет кликнуть по ней правой кнопкой мыши.
4. Кнопки «Отменить» и «Повторить».
5. Строка ввода. Это основной инструмент п ри работе в программе GeoGebra . Здесь вводятся команды и формулы, задаются значения переменных. Справа от строки ввода расположена кнопка «Список команд». С помощью дополнительных команд можно будет вводить команды и отсутствующие на клавиатуре символы.
6. Рабочая область. Все построения в программе производятся в рабочей области. Вы можете изменить масштаб с помощью колесика мыши, перемещать по рабочей области ось координат.
Использование программы на уроках алгебры
1. П ри прохождении тем “Функции и их графики ” ребята должны усвоить алгоритмы построения графиков функций, уметь исследовать поведение функции при изменении некоторых параметров. Рассмотрим простую функцию у=ах + b . Графиком функции является прямая, которую можно построить очень просто. А вот чтобы показать , как меняется график при изменении коэффициент ов а и в, при взятии в знак модуля некоторых слагаемых и самой функции поможет нам программа ГеоГебра.
Покажем эти построения на примере функции у=ах+в : в водим ползунки а и в через панель инструментов. Осуществляется это следующим образом:
1 ) Вызываем команду «Ползунок», нажимаем на рабочую область, появится карточка с названием параметра а , а дальше ОК, и также вызываем параметры в .
2 ) Затем в строку ввода записываем функцию y=ax+b , ( по английскому алфавиту) и нажать на « Enter » .
3 ) Анимация: Щелкнем правой кнопкой мыши по ползунку а и выберем «Анимировать».
Для того чтобы остановить анимацию , зайдем в свойства ползунка , нажмем опять на анимацию.
Опыт использования среды GeoGebra в преподавании математики


Учитель математики первой квалификационной категории:

Учитель математики первой квалификационной категории:
Глушкова Екатерина Владимировна
МОУ Глуховская СШ
Тема:
«Опыт использования среды GeoGebra в преподавании математики».
Формирование у учащихся представлений о научной и целостной картине мира;

Формирование у учащихся представлений о научной и целостной картине мира;
Развитие познавательного интереса, интеллектуальных и творческих способностей учащихся;
Освоение приемов логического мышления;
Проектирование и реализация личной
образовательной траектории учащимися;
5. Овладение ключевыми компетенциями.
Основные идеи школьного курса математики:
Условия возникновения опыта Первоочередная роль математического образования – это развитие мышления
Условия возникновения опыта
Первоочередная роль математического образования – это развитие мышления. Математика – единственный предмет, который профессионально направлен на развитие мозга путем решения задач.
С. Рукшин
Проблема: новый социальный заказ школьному образованию не может быть выполнен в полной мере только средствами традиционной педагогики.
Возникла необходимость в поиске средств и методических решений для соответствия новым
профессиональным компетенциям.
Обновленная нормативная база (ФГОС, Концепция развития математического образования, профессиональный стандарт педагога)
Известная методическая база
(теории, технологии, диагностики)
Недостаточно средств для решения поставленных задач
Необходимость решать новые образовательные задачи: «…Обеспечение роста творческого потенциала учеников, их готовности к применению универсальных учебных действий в жизненных ситуациях…» (ФГОС)
Концептуальная основа опыта Идея изменений: при изучении предмета использовать компьютерные чертежи в среде

Концептуальная основа опыта
Идея изменений: при изучении предмета использовать компьютерные чертежи в среде GeoGebra .
Противоречие: не смотря на высокий развивающий потенциал DGS
их почти не используют в школьном курсе математики и отсутствует
методика их использования.
Цель опыта: подобрать или составить задачи в среде GeoGebra и апробировать их использование на различных этапах урока математики и внеклассных занятиях.
Изучение теоретической базы, курсовая подготовка
В глубине души учителя осознают, что на карете прошлого далеко не уедешь, тем более, когда рядом педагогическое пространство рассекают современные автомобили.
Е. Ямбург
А.Г. Асмолов Ю.К. Бабанский С.Г
А.Г. Асмолов Ю.К. Бабанский
С.Г. Воровщиков Л.С. Выготский П.Я. Гальперин В.В. Давыдов
С.А. Бешенков
Я.А. Ваграменко
А.П. Ершов
С.Н. Поздняков
В.И. Рыжик П.И. Пидкасистый С.Л. Рубинштейн М.Н. Скаткин Н.Ф. Талызина A.B. Хуторской Т.И. Шамова Г.И.
Щукина И.С. Якиманская, др.
Актуальность состоит в необходимости широкого применения систем динамической геометрии (DGS) на уроках математики и во внеурочное время, которые позволяют быстрее, экономичнее и качественнее достигнуть цели…

Актуальность состоит в необходимости широкого применения систем динамической геометрии (DGS) на уроках математики и во внеурочное время, которые позволяют быстрее, экономичнее и качественнее достигнуть цели математического образования. Общей особенностью этих систем является возможность создания и использования динамических чертежей и геометрических конструкций.
Стремительное развитие современных интерактивных геометрических сред и, как следствие, необходимость выявления эффективных путей их использования в образовательном процессе.
Актуальность выбранной темы
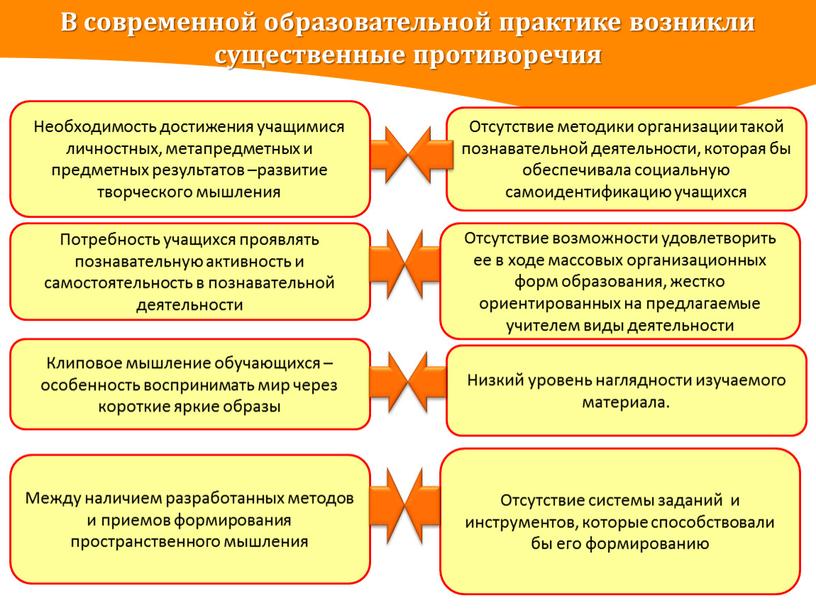
Потребность учащихся проявлять познавательную активность и самостоятельность в познавательной деятельности
Потребность учащихся проявлять познавательную активность и самостоятельность в познавательной деятельности
Отсутствие методики организации такой познавательной деятельности, которая бы обеспечивала социальную самоидентификацию учащихся
Клиповое мышление обучающихся –особенность воспринимать мир через короткие яркие образы
Низкий уровень наглядности изучаемого материала.
Между наличием разработанных методов и приемов формирования пространственного мышления
Отсутствие системы заданий и инструментов, которые способствовали бы его формированию
В современной образовательной практике возникли существенные противоречия
Необходимость достижения учащимися личностных, метапредметных и предметных результатов –развитие творческого мышления
Отсутствие возможности удовлетворить ее в ходе массовых организационных форм образования, жестко ориентированных на предлагаемые учителем виды деятельности
Одной из проблем учащихся является изучение стереометрии

Одной из проблем учащихся является изучение стереометрии.
Школьникам тяжело представлять пространственные фигуры.
Трудности в изучении стереометрии вызваны и тем, что зрительное восприятие геометрических объектов не всегда соответствует тем закономерностям, которыми этот объект обладает.
Проблема возникновения педагогического опыта
Возникает необходимость обеспечения достаточного уровня развития пространственного мышления и усвоения геометрических понятий,
повышения интереса учащихся, эффективного решения наглядности обучения, расширения возможности визуализации учебного материала, индивидуализации процесса обучения.
Цели и задачи педагогического опыта

Цели и задачи педагогического опыта
Изучить возможности геометрической динамической среды GeoGebra и методику применения этой среды на уроках математики.
1. Разработка заданий для формирования понятий курса геометрии средствами компьютерной программы GeoGebra, реализация которых обеспечит развитие пространственного мышления обучающихся, повышение мотивации при изучении наиболее сложных тем и самодиагностику;
2. Подборка прикладных задач математики, которые можно решать с применением среды GeoGebra;
3. Адаптация к условиям собственной практической деятельности.
GeoGebra — это бесплатная, кроссплатформенная динамическая математическая программа для всех уровней образования, включающая в себя геометрию, алгебру, таблицы, графы, статистику и арифметику, в одном удобном…
GeoGebra — это бесплатная, кроссплатформенная динамическая
математическая программа для всех уровней образования,
включающая в себя геометрию, алгебру, таблицы, графы,
статистику и арифметику, в одном удобном для
использования пакете. Она завоевала несколько
образовательных наград в Европе и США.
Официальный сайт программы
www.geogebra.org
Что такое GeoGebra?
Теория опыта: развитие пространственного воображения
Теория опыта: развитие пространственного воображения
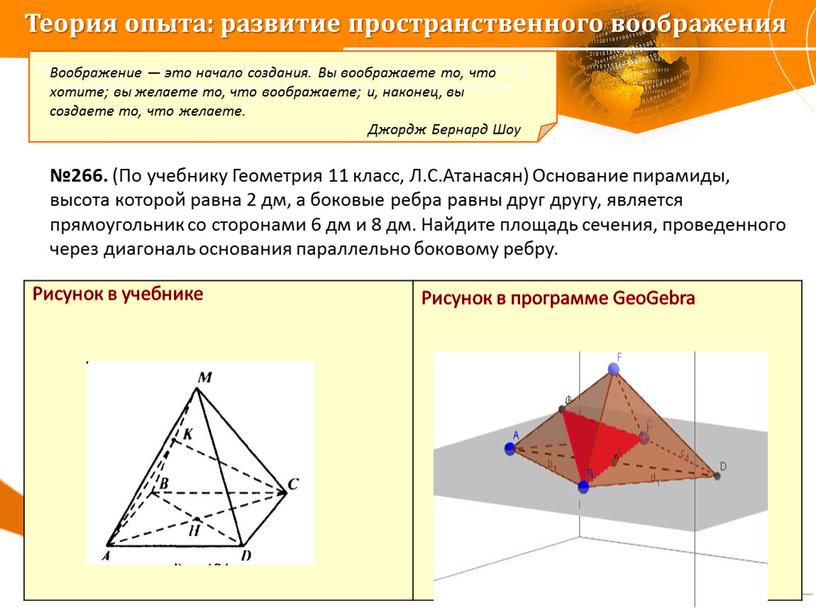
Рисунок в учебнике
Рисунок в программе GeoGebra
Воображение — это начало создания. Вы воображаете то, что хотите; вы желаете то, что воображаете; и, наконец, вы создаете то, что желаете. Джордж Бернард Шоу
Воображение — это начало создания. Вы воображаете то, что хотите; вы желаете то, что воображаете; и, наконец, вы создаете то, что желаете.
Джордж Бернард Шоу
№266. (По учебнику Геометрия 11 класс, Л.С.Атанасян) Основание пирамиды, высота которой равна 2 дм, а боковые ребра равны друг другу, является прямоугольник со сторонами 6 дм и 8 дм. Найдите площадь сечения, проведенного через диагональ основания параллельно боковому ребру.
Применение GeoGebra на уроках математики 1
Применение GeoGebra на уроках математики
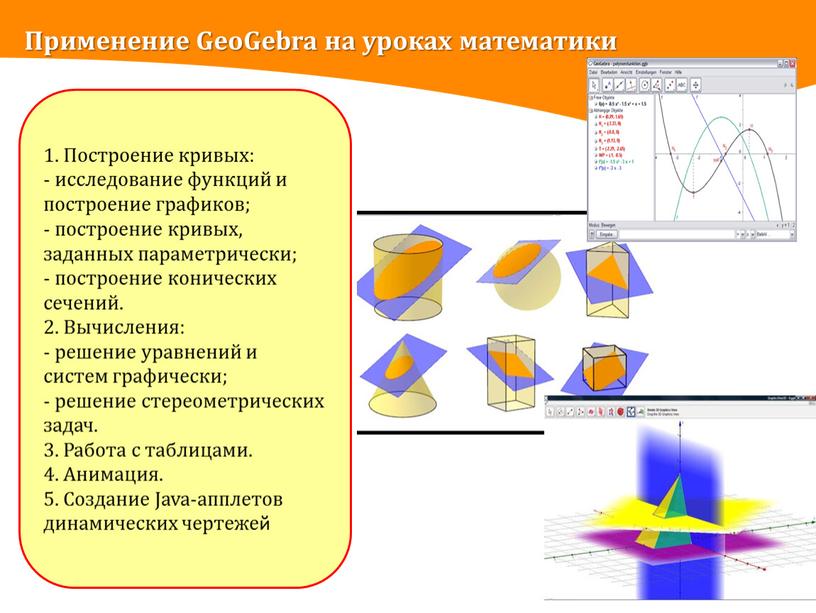
1. Построение кривых:
исследование функций и построение графиков;
построение кривых, заданных параметрически;
построение конических сечений.
2. Вычисления:
решение уравнений и систем графически;
решение стереометрических задач.
3. Работа с таблицами.
4. Анимация.
5. Создание Java-апплетов динамических чертежей
Варианты использования GeoGebra в школьной программе

Варианты использования GeoGebra в школьной программе
Изучение графиков и их применений в курсе алгебры 8-11 кл.
Построение графиков функций и исследование свойств функций по графикам.
Решение уравнений и систем уравнений с помощью графиков.
Решение неравенств и систем неравенств с помощью графиков.
Построение криволинейной трапеции и вычисление ее площади
Основные темы курса стереометрии в 10-11 кл.
1. Параллельность и перпендикулярность прямых и плоскостей в пространстве.
2. Многогранники. Решение задач, построение сечений.
3. Тела вращения. Решение задач.
4. Объемы стереометрических тел. Разные задачи на многогранники и тела вращения
Возможности программы GeoGebra

Возможности программы GeoGebra
Смотреть мой мастер-класс
Планиметрические чертежи в GeoGebra
GeoGebra как конструктор стереометрических чертежей
GeoGebra как построитель графиков функций
GeoGebra как платформа для создания интерактивных иллюстраций и тренажеров
Линейная функция
Тренажер «Линейная функция»
Квадратичная функция и дискриминант
Демонстрация «Тригонометрическая окружность»
Тренажер «Тригонометрия»
Тренажер «Рисунки по координатам»
Задача преподавания геометрии — развить у учащихся три качества: пространственное воображение, практическое понимание и логическое мышление. Следовательно, преподавание геометрии должно включать три тесно связанных, но вместе с тем и противоположных элемента: логику, наглядное представление, применение к реальности
Формируемые УУД Личностные Регулятивные
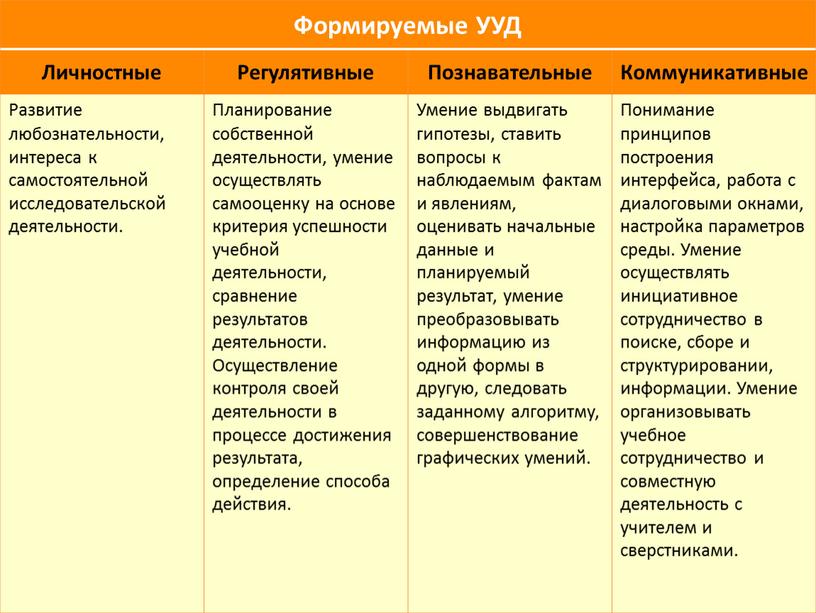
Развитие любознательности, интереса к самостоятельной исследовательской деятельности.
Планирование собственной деятельности, умение осуществлять самооценку на основе критерия успешности учебной деятельности, сравнение результатов деятельности. Осуществление контроля своей деятельности в процессе достижения результата, определение способа действия.
Умение выдвигать гипотезы, ставить вопросы к наблюдаемым фактам и явлениям, оценивать начальные данные и планируемый результат, умение преобразовывать информацию из одной формы в другую, следовать заданному алгоритму, совершенствование графических умений.
Понимание принципов построения интерфейса, работа с диалоговыми окнами, настройка параметров среды. Умение осуществлять инициативное сотрудничество в поиске, сборе и структурировании, информации. Умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.
Источник: znanio.ru
Использование программы GeoGebra на уроках математики как средство подготовки учащихся к ЕГЭ

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №28
Использование программы GeoGebra на
уроках математики как средство
подготовки учащихся к ЕГЭ
GeoGebra
www.geogebra.org
Выполнила учитель математики МБОУ СОШ №28 г. Мытищи Алышова Наталья Сергеевна
2. Что такое GeoGebra?
это бесплатная, кроссплатформенная динамическая
математическая программа для всех уровней образования,
включающая в себя геометрию, алгебру, таблицы, графы,
статистику и арифметику, в одном удобном для
использования пакете. Она завоевала несколько
образовательных наград в Европе и США.
Официальный сайт программы
www.geogebra.org
3. Установка программы
4. Выбор операционной системы
5. Установка программы
6. Программа GeoGebra
7. Пример 1. Решение задачи С4
Дан параллелограмм ABCD, AB=2, BC=3,
угол A равен 60 градусам .
Окружность с центром О касается биссектрисы
угла D и двух сторон
параллелограмма, исходящих из вершины
одного его острого угла.
Найдите площадь четырехугольника ABOD.
Источник: ppt-online.org