Информационный граф программы это

Набор данных есть совокупность данных, передаваемых между двумя вычислительны­ми модулями. На логическом уровне выделяют связи по управле­нию и связи по данным. Такие связи существуют как внутри вычис­лительного модуля, так и между модулями различных уровней вычислительного графа системы обработки. Для любого модуля выделяют входные и выходные данные.

Входные данные отобразим матрицей Н, элемент которой hik=1, если входной набор данных N1i используется вычислительным мо­дулем k. Этот же элемент hik=0, если это не имеет места.

Выходные данные формально отобразим матрицей Е, элемент которой ekj=1, если набор данных N3j получен в результате работы вычислительного модуля k. Элемент матрицы ekj=0 — в противном случае.

Матрица взаимосвязи входных и выходных данных Q=HÄE.

Элемент матрицы qij=1, если входной набор данных N1i исполь­зуется для получения выходного набора данных N3j. Элемент мат­рицы qij=0, если это не имеет места. На рис. 3.26 представлена связь вычислительного модуля ВМk с входным набором данных N1i и выходным набором данных N3j.

Графы, вершины, ребра, инцидентность, смежность

Структура модуля по преобразованию данных задается матрицей Q, связь модуля с набором данных N1i определяется матрицей Н, связь модуля с набором данных N3j — матрицей Е. Матрица Q соответствует ориентированному графу взаимосвязей между данными (этот граф получил название информационного графа системы). Вершинами графа являются родные, промежуточные и выходные наборы данных. Дуги графа отображают информационные связи между этими наборами (рис. 61).

В информационном графе системы можно выделить входные вершины, которые не имеют входных дуг и отображают первичные (входные) наборы данных. В концевых вершинах графа, которые не имеют исходящих дуг, располагаются выходные наборы данных, являющиеся результатами обработки информации и используемые для принятия решения в системе.

В остальных вершинах графа располагаются промежуточные наборы данных, которые являются внутренними по отношению к пользователю и возникают в процес­се вычислений как промежуточный результат. Отметим, что в отличие от вычислительного графа системы информационный граф может иметь контуры и петли, что объясняется необходимостью повторного обращения к отдельным наборам данных. Входные данные являются первичными, поскольку они возникают при изуче­нии производства и характеризуют исходное состояние управля­емой системы. Промежуточные и выходные данные относятся ко вторичным данным. Вторичные данные возникают в результате процесса обработки, т. е. выполнения отдельных процедур над первичными данными.

Вычислительный граф системы обработки и информационный граф системы позволяют формализованно определить инфологическую модель предметной области. В процессе обработки и накоп­ления данных формируются новые наборы данных, при этом можно различать два крайних случая:

1. Формирование набора данных на основе вычислительного алгоритма, т. е. для имеющихся входных наборов данных на основе вычислений получают выходные данные. Последовательность ис­пользования вычислительных модулей для формирования выход­ного набора данных определяется вычислительной граф-схемой ал­горитма в виде ориентированного графа без петель. В вершинах графа располагаются вычислительные модули, а дуги графа отоб­ражают отношение предшествования между ними.

Граф: определение и виды | Информатика

2. Вычисление значений набора данных по имеющимся старым значениям и по совокупности изменений, возникающих в первичном наборе данных. Эти процедуры осуществляются на основе алгорит­мов корректировки набора данных. Корректировка возможна в том случае, если корректируемый набор данных уже ранее был запро­шен и хранится в информационной базе.

Таким образом, в модели накопления данных может быть выяв­лено два основных типа алгоритма нахождения новых наборов: вычислительный алгоритм и алгоритм корректировки набора дан­ных. Реализация вычислительного алгоритма при запросе обычно необходима тогда, когда запрашиваемый набор данных не хранится в информационной базе. При наличии этого набора более удобно использовать алгоритм корректировки. Вычислительный алгоритм реализуется на базе информационного графа системы, алгоритм корректировки базируется на списке изменений, вносимых в первич­ный набор данных.

Независимо от используемого алгоритма вычислительный мо­дуль выполняет определенные процедуры, включающие в себя дей­ствия над данными. На логическом уровне возникает задача специ­фикации действий, т. е. определение входных и выходных наборов данных для действий, а также взаимосвязей между различными действиями.

При этом можно выделить два типа функциональных (логических) элементов: элементы — действия Q и элементы — объекты действий D. Элементы действия Q характеризуются внешними связями и ресурсами. Такой элемент реализует опреде­ленное преобразование над данными с использованием в качестве ресурсов элементов типа Q и элементов типа D.

В качестве объектов действий выступают данные, которые характеризуются именем, типом и значением. Тип определяет множество значений, которые принимают объекты данного типа. Объект действий задается струк­турой, т. е. составом компонентов и связей между ними. Элемент Q взаимодействует с элементами D1, D2, D3 через связи типа: 1 — «вход», 2 — «выход», 3 — «вход — выход» (рис. 62).

Совокупность элементов действий Q и элементов объектов дей­ствий, т. е. данных D, образует информационную схему. Естествен­но, что одни и те же данные могут быть использованы различными элементами действий. На рис. 63 представлена информационная схема, включающая элементы действий Q1…Q­3 и элементы данных D1…D4.

В схеме присутствуют связи типа 1 — «вход» и типа 2 — «выход». Связи первого типа формально записываются в виде D in Q, а второго типа — D out Q. Информационная схема отоб­ражается матрицей

Матрица В построена непосредственно по информационной схеме. Данные D1 используются действиями Q1 и Q2, что соответствует первой строке матрицы. Данные D2 формируются действием Q3 что отображается второй строкой матрицы.

Данные D3 вычисляются действием Q1 и используются действием Q2, что соответствует третьей строке. Данные D4 вырабатываются действием Q2 и исполь­зуются действием Q3 (четвертая строка). Исключим из информаци­онной схемы элементы действия Q и найдем связи по данным, что на логическом уровне соответствует информационному графу си­стемы. Учтем при этом частоту активизации действий. При одиноч­ном запросе суммарное количество действий, использующих дан­ные d­­i, обозначим через zii, а суммарное количество действий, использующих данные dj совместно с данными di, определим как zij. Члены zij, zij являются элементами матрицы Z=B´B t .

Для рассмотренного примера

Полученной матрице будет соответствовать граф, изображен­ный на рис. 64.

В вершинах этого графа располагаются элементы данных D1. D4, Дуги графа отображают суммарное количество дей­ствий, использующих эти данные раздельно и совместно.

Вводя в матрицу Z частоту активизаций действий f, получим матрицу

Элемент матрицы zfij показывает частоту использования данного di с учетом частоты активизации действий. Соответственно элемент zfij отображает частоту совместного использования данных di, dj. По значениям этих частот данные могут объединяться в запи­си, а записи — в массивы. При этом обеспечивается минимизация числа обращений к записям в процессе обработки и корректировки информации.

При известной частоте активизации действий, заданной мат­рицей — строкой f, нетрудно по приведенной выше методике найти ZF. Например, для f=|1 2 5|

На основе полученной матрицы данные могут быть скомпонова­ны в записи с учетом частоты их совместного использования. Учитывая, что в основе современной информационной технологии лежат данные, возникает задача выделения и локализации сильно связанных элементов данных.

Если в информационном графе системы содержится N вершин и граф отображает полносвязанную систему, то максимальное чис­ло связей составит N 2 . Для определения степени связности графа, представленного на рис. 64, найдем коэффициент совместного использования данных di, dj в виде . Элемент sij=1, если данное di всегда используется совместно с данным dj. При sij=0 данные di, dj совместно не используются. Объединяя sij при l≤i≤N, j≤l ≤N, находим матрицу коэффициентов совместного использова­ния данных. Для рассмотренного графа N=4 получаем

Элементы главной диагонали этой матрицы характеризуют вну­треннюю связность элементов данных, остальные элементы матрицы определяют связность их между собой. При sij=0 для i¹j

Получаем разделение данных на независимые компоненты. Коэф­фициент связности , он определяется совокупностью вутренних и внешних связей элементов данных, т. е. ks=ks in+ks оut.

При отсутствии внешних связей ks оut=0, кs=кs in. Внутренняя связность данных может быть определена в виде . В качестве критерия реорганизации информационной схемы используют зачастую относительный коэффициент связности . Объединение отдельных сильно связанных элементов данных позволяет увеличить значение относительного коэффициен­та связности. Этот коэффициент может быть изменен, если перераспределяются функции между элементами действий.

Источник: infopedia.su

Программные инструменты параллелизма

Аннотация: Эта лекция является вводной. В ней рассматриваются такие вопросы, как эволюция вычислительных технологий, последовательная и параллельная модели программирования, парадигмы параллельного программирования, дается обзор программных инструментов, используемых для разработки высокопроизводительных приложений

Ключевые слова: оптимизация, распараллеливание, векторизация

Презентацию к данной лекции Вы можете скачать здесь.

Эволюция вычислительных технологий

От фоннеймановской архитектуры к архитектуре многоядерной

• Фоннеймановская архитектура
• Как эволюционировала архитектура вычислительных систем
• Эволюция программных технологий

Фоннеймановская архитектура последовательная, скалярная. В «классическом» фоннеймановском компьютере параллелизм отсутствует на всех уровнях. Традиционная последовательная модель программирования, ориентированная на SISD архитектуры (по Флинну). Языки последовательного программирования.

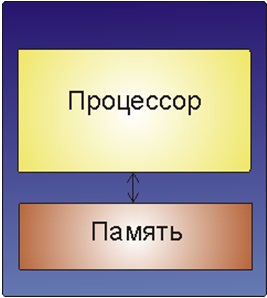
Пользователю нужна производительность. Увеличение производительности позволяет:

• решать новые, более сложные задачи;
• решать старые задачи, но быстрее;
• решать старые задачи, но с более высокой точностью.

Многие расширения фоннеймановской архитектуры используют параллелизм на разном уровне

Вычислительные системы с распределенной памятью (кластеры, MIMD по классификации Флинна) от небольших кластеров до суперкомпьютеров, занимающих первые позиции в рейтинге Top 500 Supercomputers..

Многоядерные архитектуры стали доминирующими

Первые многоядерные процессоры появились на рынке в 2005 году. Сейчас это доминирующий тип архитектур.

Вычислительная система с многоядерным процессором – параллельная вычислительная система с общей памятью, обычно SMP (Symmetric Multiprocessor System).

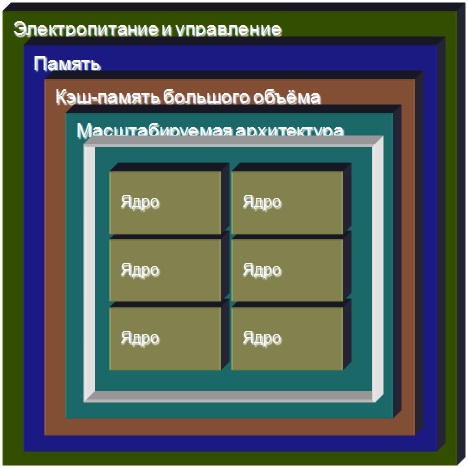
От архитектуры multicore (с небольшой многоядерностью) к архитектуре manycore (с большой многоядерностью)

Архитектура Intel® Many Integrated Core (MIC) – шаг к системам с большой многоядерностью, от 32-ядерного прототипа к системам с десятками, сотнями и т.д. ядер

Параллельное и последовательное программирование

Что происходит с данными внутри программы. Информационный граф программы

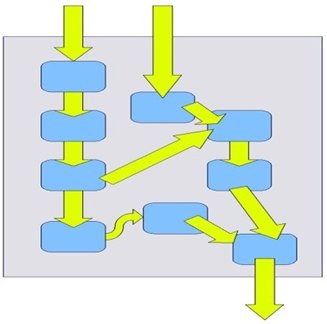
Алгоритм можно представить в виде диаграммы информационного графа.

Информационный граф описывает последовательность выполнения операций и взаимную зависимость между различными операциями или блоками операций.

Узлами информационного графа являются операции, а однонаправленными дугами каналы обмена данными.

Понятие операции может трактоваться расширенно. Это может быть оператор языка, но может быть и более крупный блок программы.

Последовательная и параллельная модели программирования

Традиционной считается последовательная модель программирования. В этом случае в любой момент времени выполняется только одна операция и только над одним элементом данных. Последовательная модель универсальна. Ее основными чертами являются применение стандартных языков программирования (для решения вычислительных задач это, обычно, Fortran и С/С++), хорошая переносимость программ и невысокая производительность.

Основными особенностями параллельной модели программирования являются более высокая производительность программ, применение специальных приемов программирования и, как следствие, более высокая трудоемкость программирования, проблемы с переносимостью программ. Параллельная модель не обладает свойством универсальности.

Параллельная модель программирования

В параллельной модели программирования появляются проблемы, непривычные для программиста, привыкшего заниматься последовательным программированием. Среди них: управление работой множества процессоров, организация межпроцессорных пересылок данных и другие.

Повышенная трудоемкость параллельного программирования связана с тем, что программист должен заботиться:

• об управлении работой множества процессов;
• об организации межпроцессных пересылок данных;
• о вероятности тупиковых ситуаций (взаимных блокировках);
• о нелокальном и динамическом характере ошибок;
• о возможной утрате детерминизма («гонки за данными»);
• о масштабируемости;
• о сбалансированной загрузке вычислительных узлов.

Источник: intuit.ru

8 Распараллеливание программ с использованием моделей вычислительных процессов Модели программ

Свойства программ определяют их информационную структуру, которая характеризует ее элементы и связь их друг с другом. Возможны подходы к изучению информационной структуры:

1. Денотационный – исследование состояния памяти, соответствующих состояний переменных и изменение состояния памяти в ходе выполнения программы.
2. Операционный – исполнение программы представляется в виде набора исполняемых выполняемых операций, связанных между собой. Порождает графовые модели программ.

Графовые модели характеризуются:

1. Множеством вершин, соответствующих действиям в программе.
2. Множеством дуг, определяющих отношения разного вида (по управлению, по данным и т.д.).

Операционный подход определяет два типа данных (блоков) в моделях программ:

• Преобразователи (выполняют действия с данными);
• Распознаватели – определение порядка срабатывания преобразователей.

При обозначении через S – множество преобразователей, R – множество распознавателей, то

Определение видов графовых моделей будет осуществлено применительно к рассмотренному тексту программы:

Для данной программы должны быть определены данные:

Существуют два типа отношений между действиями в программе:

1.Выполнение одного действия непосредственно за другим. Запуск последующего действия выполняется после окончания реализации предшествующего. Такой тип отношений называют связью по управлению. То есть связь по управлению определяется последовательностью запуска операторов программы.

2. Информационный – характеризует использование аргументов для нижестоящих операторов, являющихся результатами операторов предшествующих (отношения связи по данным).

Оба типа отношений упорядочивают множество операторов в программе.

8.1 Граф управления

Вершина графа является оператором (преобразователь либо распознаватель). Между вершинами связей, определяется взаимодействие между операторами, соответствующее отношениям передачи управления.

Информационный граф программы

Основа графа – вершинный преобразователь. В результате граф определяет поток информации между операторами в программе. Дуги определяют отношения информационной зависимости между операторами – вершинами. Таким образом, вершины могут быть связаны дугами, если между ними существует информационная зависимость.

Выводы, связанные с внутренними свойствами программы:

Свойства программы характеризуются либо множеством операторов, либо множеством переменных, идентифицируемых на основе состояния памяти.

Система управляющих связей в программе (связей по управлению), определяющих последовательность или порядок задается в виде графа. Дуга графа определяет передачу управления между операторами. При разделении программы на операторы отсутствует информация о внутренней структуре оператора и структуре памяти.

Формализация представления управляющего графа программы

Задан алфавит символов, сопоставляемых с множеством операторов.

Операторы преобразователи и распознаватели. Функция L(p) сопоставляет некоторой вершине p графа оператор программы:

Через L(p) обозначим оператор а, сопоставляемый с вершиной. Таким образом, граф может быть представлен в виде (G, L). G – множество вершин, L – некоторая разметка графа, сопоставляющая вершине определенные операторы.

Пример управляющего графа программы (рис.8):

Рисунок 8 – Пример управляющего графа

Транзитивные замыкания – метод потокового анализа программы предполагает транзитивные замыкания отношений следования между операторами программы (между вершинами управляющего графа).

При анализе потоков управления определяются отношения обязательного предшествования для операторов программы, вершин графа, то есть какие операторы должны предшествовать рассматриваемому. Аналогично определяются отношения обязательной преемственности (транзитивное замыкание тех вершин графа, которые являются последующими за данным).

Источник: studfile.net