Л огические операторы – это операторы, которые принимают в качестве аргументов логические значений (ложь или истину) и возвращают логическое значение. Как и обычные операторы, они могут быть одноместными (унарными, т.е. принимать один аргумент), двуместными (бинарные, принимают два аргумента), трёхместными и т.д.
Особенностью языка си является то, что в нём нет типа, хранящего булево значение (ложь или истину). В си ложью (логическим нулём) считается целочисленный 0, а любое ненулевое целое будет логической истиной. Например
#include #include void main() < char boolValue = -71; if (boolValue) < printf(«boolValue is true»); >else < printf(«boolValue is false»); >_getch(); >
Логические значения обычно порождаются операторами сравнения (==, !=, >, =. <=).
В языке си представлено три логических оператора: И, ИЛИ и НЕ. Начнём с самого простого
Логическое отрицание
О ператор НЕ (NOT) используется для того, чтобы инвертировать значение аргумента. Т.е., если ему передали истину, то он вернёт ложь, если получил ложь в качестве аргумента, то вернёт истину.
Логические элементы И, ИЛИ, НЕ
| 1 | |
| 1 |
В си отрицание представлено оператором !. Например
#include #include void main() < int i = 0; if (i) < printf(«i is truen»); >if (!i) < printf(«i is not truen»); >if (!!i) < printf(«i is not not truen»); >if (. i) < printf(«i is not not not truen»); >_getch(); >
Как и в обычной логике, здесь действует закон двойного отрицания – отрицание отрицания можно опустить.
Логическое И
О ператор И (AND, логическое умножение) возвращает истину тогда и только тогда, когда оба аргумента являются истиной.
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
В си логическое умножение представлено оператором . Например, задача – в кружок военных спейсмаринов допускаются только совершеннолетние граждане мужского пола. То есть, претендентом может стать только тот, для которого одновременно два условия являются истиной
#define _CRT_SECURE_NO_WARNINGS #include #include void main() < char gender; unsigned int age; printf(«Enter gender (‘M’ or ‘F’)n»); scanf(«%c», printf(«Enter agen»); scanf(«%u», if (gender == ‘M’ age >17) < printf(«Wellcome»); >else < printf(«Go away»); >_getch(); >
Оператор И может применяться последовательно к нескольким аргументам. Для него действует ассоциативный и коммутативный законы. Усовершенствуем программу, будем также вводить рост:
#define _CRT_SECURE_NO_WARNINGS #include #include void main() < char gender; unsigned int age; unsigned int height; printf(«Enter gender (‘M’ or ‘F’)n»); scanf(«%c», printf(«Enter agen»); scanf(«%u», printf(«Enter heightn»); scanf(«%u», if (gender == ‘M’ age >17 height >= 180) < printf(«Wellcome»); >else < printf(«Go away»); >_getch(); >
Также условие могло быть записано
Элементы ИЛИ, И, НЕ в логических схемах РЗА
(gender == ‘M’ age > 17) height >= 180
gender == ‘M’ (age > 17 height >= 180)
(age > 17 height >= 180) gender == ‘M’
Логическое ИЛИ
О ператор логическое ИЛИ (логическое сложение, OR) истинен тогда, когда истиной является хотя бы один его аргумент.
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 | 1 |
В си ИЛИ представлен оператором ||. Например, усовершенствуем программу: теперь пол можно вводить как большой, так и маленькой буквой
#define _CRT_SECURE_NO_WARNINGS #include #include void main() < char genderInput; char gender; unsigned int age; unsigned int height; printf(«Enter gender (‘M’ or ‘F’)n»); scanf(«%c», printf(«Enter agen»); scanf(«%u», printf(«Enter heightn»); scanf(«%u», if (genderInput == ‘M’ || genderInput == ‘m’) < gender = 1; >else < gender = 0; >if ((age > 17 height >= 180) gender) < printf(«Wellcome»); >else < printf(«Go away»); >_getch(); >
Как и в случае оператора И, ИЛИ коммутативен и ассоциативен.
Операторы можно перемешивать друг с другом, создавая сложные операторы
#define _CRT_SECURE_NO_WARNINGS #include #include void main() < char gender; unsigned int age; unsigned int height; printf(«Enter gender (‘M’ or ‘F’)n»); scanf(«%c», printf(«Enter agen»); scanf(«%u», printf(«Enter heightn»); scanf(«%u», if ((age >17 height >= 180) (gender == ‘M’ || gender == ‘m’)) < printf(«Wellcome»); >else < printf(«Go away»); >_getch(); >
Стоит только помнить о том, что оператор отрицания имеет больший приоритет, чем И или ИЛИ, поэтому будет выполняться в первую очередь. Если может случиться ситуация, когда порядок выполнения не ясен, определите его с помощью скобок.
Пример: закон де-Моргана. Чтобы сменить И на ИЛИ (или наоборот), необходимо инвертировать значения всех операндов, заменить И на ИЛИ (или ИЛИ на И) и инвертировать конечный результат. В случае с нашим условием
(age > 17 height >= 180) (gender == ‘M’ || gender == ‘m’)
Рассмотрим сначала кусок
(age > 17 height >= 180)
Меняем все значения на обратные
(!(age > 17) !(height >= 180))
заменяем оператор на ||
(!(age > 17) || !(height >= 180))
и инвертируем ответ
!(!(age > 17) || !(height >= 180))
Как видим, результат тот же. Очевидно, что
!(age > 17)
Таким образом, изменим условие
Поменяем таким же образом вторую скобку
(gender == ‘M’ || gender == ‘m’)
!(gender != ‘M’ gender != ‘m’)
Теперь можно применить это же правило и для всего выражения
Порядок выполнения логических операторов
Р ассмотрим выражение
где a, b, c, d – логические значения. Всё выражение равно истине тогда и только тогда, когда все операнды истинны. Если хотя бы один из операндов ложь, то остальные уже не важны. Поэтому, для оптимизации работы, вычисление происходит слева направо и останавливается, как только был найден первый операнд, равный нулю.
В си оператор присваивания может возвращать значение. Иногда он используется непосредственно в условии:
#define _CRT_SECURE_NO_WARNINGS #include #include #include void main() < int a = 0; int *p = if (a (p = (int*) malloc(sizeof(int) * 2))) < printf(«memory was allocated»); >free(p); _getch(); >
В данном случае, оператор malloc не будет выполнен, так как первый операнд a равен 0 (соответственно, всё выражение равно нулю). Таким образом, оператор free попытается очистить память, которую не может очистить (т.к. p продолжит ссылаться на a). Если же мы поменяем a = 1, то всё отработает без проблем.
То же самое происходит и при выполнение ||. Выражение
выполняется слева направо до тех пор, пока не встретит первое ненулевое значение. После этого выполнение останавливается, так как известно, что всё выражение равно истине.
Очевидно, что это касается не только оператора присваивания, но и любого другого вызова функции. Например, в этом случае функции foo будет вызвана, bar нет.
#define _CRT_SECURE_NO_WARNINGS #include #include #include int foo() < printf(«foon»); return 0; >int bar() < printf(«barn»); return 0; >void main() < int a = 0, b = 1; if (a || foo() || b || bar()) < printf(«OKn»); >_getch(); >
Вывод – не используйте присваивания и вызовов функций (особенно, если они изменяют состояние программы) внутри условий.

Всё ещё не понятно? – пиши вопросы на ящик
Источник: learnc.info
Логические операции в C++
Так как в предыдущей статье, я впервые использовал логическую операцию, расскажу, какие они бывают, сколько их и как ими пользоваться.
В С++ существует три логические операции:
- Логическая операция И , нам уже известная;
- Логическая операция ИЛИ || ;
- Логическая операция НЕ ! или логическое отрицание.
Логические операции образуют сложное (составное) условие из нескольких простых (два или более) условий. Эти операции упрощают структуру программного кода в несколько раз. Да, можно обойтись и без них, но тогда количество ифов увеличивается в несколько раз, в зависимости от условия. В следующей таблице кратко охарактеризованы все логические операции в языке программирования С++, для построения логических условий.
| И | a == 3 b > 4 | Составное условие истинно, если истинны оба простых условия | |
| ИЛИ | || | a == 3 || b > 4 | Составное условие истинно, если истинно, хотя бы одно из простых условий |
| НЕ | ! | !( a == 3) | Условие истинно, если a не равно 3 |
Сейчас следует понять разницу между логической операцией И и логической операцией ИЛИ , чтобы в дальнейшем не путаться. Пришло время познакомиться с типом данных bool –логический тип данных. Данный тип данных может принимать два значения: true (истина) и false (ложь). Проверяемое условие в операторах выбора имеет тип данных bool . Рассмотрим принцип работы следующей программы, и все будет понятно со всеми этими логическими операциями.
// or_and_not.cpp: определяет точку входа для консольного приложения. #include «stdafx.h» #include using namespace std; int main(int argc, char* argv[]) < bool a1 = true, a2 = false; // объявление логических переменных bool a3 = true, a4 = false; cout << «Tablica istinnosti log operacii » << endl; cout << «true false: » << ( a1 a2 ) << endl // логическое И << «false true: » << ( a2 a1 ) << endl << «true true: » << ( a1 a3 ) << endl << «false false: » << ( a2 a4 ) << endl; cout << «Tablica istinnosti log operacii ||» << endl; cout << «true || false: » << ( a1 || a2 ) << endl // логическое ИЛИ << «false || true: » << ( a2 || a1 ) << endl << «true || true: » << ( a1 || a3 ) << endl << «false || false: » << ( a2 || a4 ) << endl; cout << «Tablica istinnosti log operacii !» << endl; cout << «!true: » << ( ! a1 ) << endl // логическое НЕ
Строки 9 и 10 вам должны быть понятны, так как здесь инициализируются переменные типа bool . Причем каждой переменной присваивается значение true или false . Начиная с 9-й строки и заканчивая 20-й , показано использование логических операций. Результат работы программы (см. Рисунок 1).
CppStudio.com
Tablica istinnosti log operacii true false: 0 false true: 0 true true: 1 false false: 0 Tablica istinnosti log operacii || true || false: 1 false || true: 1 true || true: 1 false || false: 0 Tablica istinnosti log operacii ! !true: 0 !false: 1 Для продолжения нажмите любую клавишу . . .
Рисунок 1 — Логические операции С++
Наверное, у вас возникает вопрос, «А что это за нолики и единички?». Если есть вопрос, то на него нужно ответить. Отвечаю: «Нолик-это представление логического значения false (ложь), ну а единички – это логическое true (истина)». Коротко поясню некоторые моменты. Составное условие с использованием логического И истинно только в том случае, когда истинны оба простых условия.
Во всех остальных случаях составное условие ложно. Составное условие с использованием логического ИЛИ ложно только в том случае, когда ложные оба простых условия. Во всех остальных случаях составное условие истинно.
Логическое отрицание НЕ является унарной операцией, и она не комбинирует два условия, в отличие от логических операций И и ИЛИ , которые являются бинарными операциями. Логическое отрицание позволяет перевернуть смысл условия, что в некоторых случаях очень удобно. Условие с логическим отрицанием истинно в том случае, если это же условие ложно без отрицания, и наоборот.
Источник: cppstudio.com
Логические элементы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и их таблицы истинности
Электронные логические схемы широко используются в калькуляторах, компьютерах, телефонных станциях и во всех приложениях, где задействованы системы с двумя состояниями.
Система с двумя состояниями имеет только два уровня в любой точке, они называются «включено» или «выключено», «да» или «нет», «вверх» или «вниз» и так далее. Логические элементы — это небольшие электронные подсистемы, которые выполняют логические решения НЕ, И, ИЛИ и т. д., встроенные в любое цифровое электронное оборудование.
Цифровые схемы — это тип электронных схем, в которых сигналы обычно имеют два уровня напряжения и обозначаются цифрами 0 и 1, что позволяет использовать алгебру логики, поэтому эти схемы называются логическими схемами.
Л огические схемы являются основными элементами современной электроники. Благодаря пониженной чувствительности к помехам цифровые схемы обеспечивают лучшие результаты и меньшую интенсивность отказов. Логические элементы можно использовать во многих электронных проектах.
Используя логические элементы и полагаясь на логическую алгебру, мы можем создавать и проектировать различные системы, такие как системы сигнализации, цифровые радиоприемники или даже компьютер.
Логические схемы включают логические элементы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ. Булевы функции, используемые в логических схемах, представляют собой математические модели логических схем.

Что такое логические элементы
Электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными, называется логическим элементом. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня.
Операнды в данном случае подаются в двоичной системе счисления — на вход логического элемента поступают сигналы в форме напряжения высокого или низкого уровня, которые и служат по сути входными данными. Так, напряжение высокого уровня — это логическая единица 1 — обозначает истинное значение операнда, а напряжение низкого уровня 0 — значение ложное. 1 — ИСТИНА, 0 — ЛОЖЬ.
Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления. Для всех видов логических элементов, независимо от их физической природы, характерны дискретные значения входных и выходных сигналов.
Все цифровые логические схемы можно отнести к одной из двух категорий: либо к комбинационным (также называемым комбинаторными), либо к последовательным логическим схемам.
Выходной логический уровень комбинационной схемы зависит только от текущих логических уровней на входах схемы. И наоборот, последовательные логические схемы имеют характеристику памяти, из-за чего выход последовательной схемы зависит не только от текущих входных условий, но и от текущего состояния выхода схемы.
Основным строительным блоком комбинационных схем является логический элемент. Тремя простейшими функциями логических элементов являются НЕ, И и ИЛИ.
Логический элемент — это базовый строительный блок логических схем, который выполняет логическую функцию. Обычно он имеет один или несколько входов и один выход. Значение на выходе логического члена является функцией входных значений. Используя логические элементы И, ИЛИ и НЕ, можно реализовать любую логическую схему и, следовательно, любую цифровую систему.
Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных.
Логическая функция — это функция, которая возвращает логические значения для конечного числа входных параметров. Она используется в математической логике, в области теории управления, в цифровой и микропроцессорной технике. Параметры булевой функции являются булевыми переменными.
Логическую функцию можно задать с помощью словесного описания, таблицы истинности, аналитически в виде алгебраического выражения (логического уравнения) или графически с логическими символами.
С уществуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.
Логические элементы реализуют элементарные логические функции. Они используются для построения логических схем большей сложности.

В зависимости от устройства схемы элемента, от ее электрических параметров, логические уровни (высокие и низкие уровни напряжения) входа и выхода имеют одинаковые значения для высокого и низкого (истинного и ложного) состояний.

Традиционно логические элементы выпускаются в виде специальных радиодеталей — интегральных микросхем
Логические операции, такие как конъюнкция, дизъюнкция, отрицание и сложение по модулю (И, ИЛИ, НЕ, исключающее ИЛИ) — являются основными операциями, выполняемыми на логических элементах основных типов.
Используя логические элементы И, ИЛИ и НЕ, можно реализовать любую логическую схему и, следовательно, цифровую систему. Члены И и ИЛИ дополняют друг друга с помощью члена НЕ. Это значит, что их можно подменять друг другом удобным способом. Любая цифровая система может быть реализована только с помощью логических элементов И-ИЛИ или НЕ-ИЛИ или И и НЕ или ИЛИ и НЕ (всегда достаточно элементов с двумя входами).
Далее рассмотрим каждый из этих типов логических элементов более внимательно.
Логический элемент «И» — конъюнкция, логическое умножение, AND
«И» — логический элемент, выполняющий над входными данными операцию конъюнкции или логического умножения. Данный элемент может иметь от 2 до 8 (наиболее распространены в производстве элементы «И» с 2, 3, 4 и 8 входами) входов и один выход.
Условные обозначения логических элементов «И» с разным количеством входов приведены на рисунке. В тексте логический элемент «И» с тем или иным числом входов обозначается как «2И», «4И» и т. д. — элемент «И» с двумя входами, с четырьмя входами и т. д.
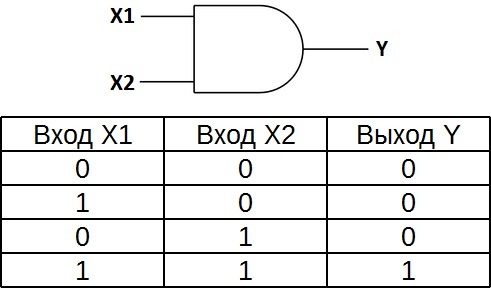
Таблица истинности для элемента 2И показывает, что на выходе элемента будет логическая единица лишь в том случае, если логические единицы будут одновременно на первом входе И на втором входе. В остальных трех возможных случаях на выходе будет ноль.
На западных схемах значок элемента «И» имеет прямую черту на входе и закругление на выходе. На отечественных схемах — прямоугольник с символом «https://electricalschool.info/electronica/1918-logicheskie-jelementy-i-ili-ne-i-ne-ili.html» target=»_blank»]electricalschool.info[/mask_link]