Вообщем нужно написать программу на паскале, которая решает систему нелинейных алгебраических уравнений и строит графики. Программа по большому счёту уже сделана, но есть небольшие косяки. Поэтому и прошу помочь. Задание:
графически и численно решить систему нелинейных алгебраи-ческих уравнений, на примере поиска точек пересечения двух функций. Исходные данные: график строится по исходным данным, определяемым в виде констант в программе: а) координаты верхнего левого угла прямоугольника, в котором должен быть расположен график; б) размеры прямоугольника; в) количество линий координатной сетки по каждой из осей; г) диапазон изменения аргумента;
Вот исходники (вместе со всеми модулями):
А вот так должна в идеале выглядеть эта программа:
res.rar Модули Consts, Types, Draw1 и Mathem1 врятли нужно менять Недочёты в Draw2, Mathem2 или самой программе, из за этого график и вылазиет за границы. Почти ко всем дествиям программы есть комментарии. Заранее благодарю!
Код к задаче: «Графическое решение системы нелинейных алгебраических уравнений»
Листинг программы
7 класс, 35 урок, Графическое решение уравнений
<*********** Процедуры и функции для работы с графикой *************>unit Draw2; interface uses consts,types,graph,crt,sysutils; < Нарисовать оси >procedure DrawAxis(var Rect;Xo,Yo,Color:word); < Рисование граничных значений по углам рамки >procedure DrawBounds(Xmin,Xmax,Ymin,Ymax:real;var Rect:trect;Color:word); < Рисование координатной сетки >procedure DrawGridLines(NgrX,NgrY:word;var Rect:trect;Color:word); < Вывод координат точек пересечения >procedure WriteCoord(var RootMas;K:word;var Rect;Color:word); implementation < Нарисовать оси >procedure DrawAxis(var Rect;Xo,Yo,Color:word); var oldcolor:word; begin oldcolor:=getcolor; setcolor(color); line(Xo,OriginY,Xo,OriginY+Ny); line(OriginX,Yo,OriginX+Nx,Yo); setcolor(oldcolor); end; < Рисование граничных значений по углам рамки >procedure DrawBounds(Xmin,Xmax,Ymin,Ymax:real;var Rect:trect;Color:word); begin outtextxy(rect.origin.x,rect.origin.y+rect.size.y+15,floattostr(Xmin)); outtextxy(rect.origin.x+rect.size.x,rect.origin.y+rect.size.y+15,floattostr(Xmax)); outtextxy(rect.origin.x-30,rect.origin.y+rect.size.y,floattostr(Ymin)); outtextxy(rect.origin.x-30,rect.origin.y,floattostr(Ymax)); end; < Рисование координатной сетки >procedure DrawGridLines(NgrX,NgrY:word;var Rect:trect;Color:word); var oldcolor:word; dx,dy,x0,y0,x1,y1:word; begin oldcolor:=getcolor; setcolor(color); dx:=round(rect.size.x/ngrx); dy:=round(rect.size.y/ngry); y1:=rect.origin.y+rect.size.y; x0:=rect.origin.x; while x0 procedure WriteCoord(var RootMas;K:word;var Rect;Color:word); begin end; end.
Источник: studassistent.ru
Программа для решения уравнения графически
Решение системы уравнений графическим методом средствами MS Excel
Цели и задачи.
Решение системы линейных уравнений графическим методом. 7 класс.
- Развитие приемов умственной деятельности, формирование и развитие функционального мышления учащихся, развитие познавательных потребностей учащихся, создание условий для приобретения опыта работы учащихся в среде ИКТ.
- Достижение сознательного усвоения учебного материала учащимися, работа над повышением грамотности устной речи, правильного использования компьютерных терминов.
- Научить применять возможности MS Excel в повседневной жизни, в познавательной деятельности.
- Закрепить навыки создания таблиц и диаграмм.
- Научить решать систему уравнений графическим методом, исследовать график функции.
Оборудование урока: компьютеры, мультимедиа проектор.
Программное обеспечение: Windows XP, пакет программ MS Office 2003.
Тема нашего урока тесно связана с математикой разделы “Графики функций” и “Решение систем уравнений”. Поэтому нам понадобятся ранее полученные навыки. Но мы постараемся упростить нашу задачу с помощью применения современных вычислительных средств.
Запишите в тетради тему урока и укажите дату.
Назовите мне кого из класса сегодня нет.
Давайте вспомним, что такое уравнение, и как его можно решить графически.
Назовите, пожалуйста, что в математике называют уравнением, решением уравнения и системой уравнений.
(Учащиеся приводят определения)
Уравнение – это математическое выражение, содержащее неизвестную величину (переменную) и 0 с правой стороны от знака =.
Система уравнений – несколько связанных уравнений, имеющих одинаковые обозначения неизвестных величин (переменных).
Решением уравнения – называют такое значение неизвестной величины, при подстановке которого левая часть выражения принимает значение 0. И мы получаем верное равенство.
Но, с другой стороны, подобное выражение можно представить как функцию с зависимой и независимой величинами. Если мы слева от знака = поставим Y, а справа заданное выражение. Y – зависимая величина, Х – независимая величина. В этом случае Решением уравнения является точка пересечения графика функции с осью ОХ.
Для решения уравнения графическим методом необходимо рассчитать значения функции в ключевых точках с координатой Х (Х меняется в диапазоне допустимых значений), нанести эти точки на систему координат, построить график функции и определить координаты точки пересечения графика с осью ОХ.
Это достаточно сложная задача. Нужно достаточно много вычислений и аккуратное построение графика функции. Также мы заранее не можем сказать, из какого диапазона чисел необходимо брать значения Х.
Но эту задачу может взять на себя ЭВМ.
Система уравнений: Калькулятор графического метода
Инструкции: Используйте этот калькулятор для решения системы двух линейных уравнений графическим методом. Пожалуйста, введите два действительных линейных уравнения в поля ниже:
Подробнее о графическом методе решения линейных систем
Системы линейных уравнений очень часто встречаются в различном контексте алгебры. Чаще всего в базовых курсах алгебры встречаются системы 2 на 2, которые состоят из двух линейных уравнений и двух переменных.
Такие системы «два на два» часто появляются при решении задач со словами, задач на пропорции и задач на присваивание с ограничением. Естественно, более крупные системы (с большим количеством переменных и уравнений) также распространены, здесь мы сосредоточимся только на системах 2×2, потому что их мы можем изобразить графически.
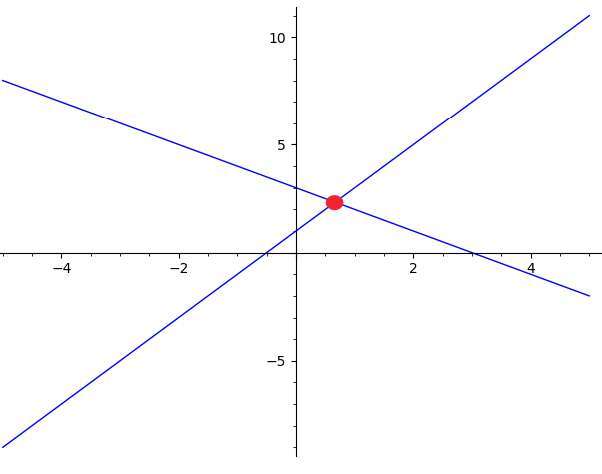
Как пользоваться графическим методом
Графический метод состоит в представлении каждого из линейных уравнений в виде линии на графике. Затем нам нужно найти точки пересечения двух прямых , используя наблюдение, что точка пересечения прямой (если она существует) будет решением системы.
Что произойдет, если перекрестка не существует? Это было бы в случае, если линии параллельны, но не являются одной и той же линией, и в этом случае пересечения нет. Правило понятно: когда между линиями нет пересечения, у системы нет решения.
Возможен и третий случай: прямые могут быть параллельными, но на самом деле идентичными (то есть это одна и та же линия). Итак, сколько у вас точек пересечения? Да, вы правы: у вас есть бесконечные точки пересечения, а значит, у вас есть бесконечные решения.
Решение систем уравнений путем графического отображения ответов
Итак, методология проста: вы начинаете с линейной системы, и первое, что вы делаете, это график двух линейных уравнений .
Затем вы смотрите на график и оцениваете, пересекаются ли линии только в одной точке (что происходит, если линии имеют разные наклоны, и в этом случае у вас есть уникальное решение).
Если нет, посмотрите, параллельны ли они и различны, и в этом случае решений нет. В противном случае, если две прямые равны, то у нас есть бесконечные решения.
Как решить систему уравнений на графическом калькуляторе?
Все системы работают по-разному. В этом случае с этим графическим калькулятором все, что вам нужно сделать, это ввести два линейных уравнения, даже если они не полностью упрощены. Калькулятор сначала попытается вывести линии на пересечение наклона и предоставит вам график и приблизительную оценку решения.
Различные калькуляторы дают разные результаты, но большое преимущество этого калькулятора в том, что он обеспечивает все этапы процесса.
Как вы пишете системы уравнений из графика?
Линейные функции однозначно связаны. То есть одно линейное уравнение связано только с одним линейным уравнением и только с одной линией, и наоборот, линия связана только с одним линейным уравнением и одним линейным уравнением.
Итак, чтобы написать системы уравнений с графика, нужно работать с каждой линией отдельно. Возьмите одну линию и определите две точки на линии. С этими двумя точками вы можете вычислить наклон линии .
Затем, с наклоном линии и точкой пересечения по оси y, вы можете запишите уравнение прямой в виде точки пересечения .
Источник: mathcracker.com