Сегодня мы начинаем говорить о теории графов. Это не структура данных и не метод решения задача. Графы – это способ представления и обработки данных в виде не просто множества объектов заданного класса, но и с учетом связей между ними.
Теория графов — один из обширнейших разделов дискретной математики, широко применяется в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических цепей, коммуникации, психологии, социологии, лингвистике, других областях знаний. Теория графов систематически и последовательно изучает свойства графов, о которых можно сказать, что они состоят из множеств точек и множеств линий, отображающих связи между этими точками. Основателем теории графов считается Леонард Эйлер (1707-1882), решивший в 1736 году известную в то время задачу о кёнигсбергских мостах.
Графы строят для того, чтобы отобразить отношения на множествах . Пусть, например, множество A = — множество людей, а каждый элемент будет отображён в виде точки. Множество B = — множество связок (прямых, дуг, отрезков — пока не важно). На множестве A задано отношение знакомства между людьми из этого множества. Строим граф из точек и связок.
BP2-3-1-07 Простейшая реализация графа
Связки будут связывать пары людей, знакомых между собой. Естественно, число знакомых у одних людей может отличаться от числа знакомых у других людей, а некоторые вполне могут и не быть ни с кем знакомы (такие элементы будут точками, не соединёнными ни с одной другой). Вот и получился граф!
То, что мы сначала назвали «точками», следует называть вершинами графа, а то, что называли «связками» — рёбрами графа.
Теория графов не учитывает конкретную природу множеств A и B. Существует большое количество самых разных конкретных задач, при решении которых можно временно забыть о специфическом содержании множеств и их элементов. Эта специфика никак не сказывается на ходе решения задачи, независимо от её трудности! Например, при решении вопроса о том, можно ли из точки a добраться до точки b, двигаясь только по соединяющим точки линиям, неважно, имеем ли мы дело с людьми, городами, числами и т.д. Но, когда задача решена, мы получаем решение, верное для любого содержания, которое было смоделировано в виде графа. Не удивительно поэтому, что теория графов — один из самых востребованных инструментов при создании искусственного интеллекта: ведь искусственный интеллект может обсудить с собеседником и вопросы любви, и вопросы музыки или спорта, и вопросы решения различных задач, причем делает это без всякого перехода (переключения), без которого в подобных случаях не обойтись человеку.
А теперь строгие математические определения графа.
2. Основные понятия теории графов.
Графом называется система объектов произвольной природы (вершин) и связок (рёбер), соединяющих некоторые пары этих объектов.
Пусть V – (непустое) множество вершин, элементы v∈V – вершины. Граф G = G(V) с множеством вершин V есть некоторое семейство пар вида: e = (a, b), где a,b∈V, указывающих, какие вершины остаются соединёнными. Каждая пара e = (a, b) — ребро графа. Множество U — множество рёбер e графа. Вершины a и b – концевые точки ребра e.
Графы, вершины, ребра, инцидентность, смежность
Графы как структура данных. Широким применением теории графов в компьютерных науках и информационных технологиях обусловлено добавлением к вышеизложенным определениям понятия графа как структуры данных. В компьютерных науках и информационных технологиях граф определяется как нелинейная структура данных.
Что же тогда — линейная структура данных и чем от них отличаются графы? Линейные структуры данных характеризуются тем, что связывают элементы отношениями типа «простого соседства». Линейными структурами данных являются, например, массивы, таблицы, списки, очереди, стеки, строки. В противоположность им нелинейные структуры данных — такие, в которых элементы располагаются на различных уровнях иерархии и подразделяются на три вида: исходные, порождённые и подобные. Итак, граф — нелинейная структура данных.
Слово граф греческого происхождения, от слов «пишу», «описываю». То есть, любой граф описывает отношения. И наоборот: любое отношение можно описать в виде графа.
Ориентированные и неориентированные графы.
Графы, в которых все рёбра являются звеньями (порядок двух концов ребра графа не существенен), называются неориентированными.
Графы, в которых все рёбра являются дугами (порядок двух концов ребра графа существенен), называются ориентированными графами.
Неориентированный граф может быть представлен в виде ориентированного графа, если каждое его звено заменить на две дуги, имеющие противоположные направления.
Связный граф — граф , содержащий ровно одну компоненту связности . Это означает, что между любой парой вершин этого графа существует как минимум один путь .
Граф заданного типа называют полным, если он содержит все возможные для этого типа рёбра (при неизменном множестве вершин). Так, в полном обыкновенном графе каждая пара различных вершин соединена ровно одним звеном.
Деревом называется связный граф без циклов. Любые две вершины дерева соединены лишь одним маршрутом:
Смежность вершин графа — это когда две вершины графа соединены ребром.
Зададимся вопросом: можно ли поместить слона в компьютер? Ответ: можно, если слона смоделировать в виде графа, в котором вершинами являются части его тела, а рёбра соединяют те части тела, которые соединены в слоне как биологическом объекте. При этом получившийся граф должен быть представлен в памяти компьютера в понятном компьютеру виде.
3. Способы представления графа в памяти компьютера.
В связи с широким применением графов в программировании и информационных технологиях вообще возникает вопрос о представлении графа в виде структуры данных. Различные способы представления графов в памяти компьютера отличаются объёмом занимаемой памяти и скоростью выполнения операций над графами.
Наиболее часто используются две такие структуры данных — матрица смежности и список инцидентности.
Матрицы смежности
Матрица смежности позволяет установить множество вершин, соседних с заданной (то есть рассматриваемой в конкретной задаче), не прибегая к полному просмотру всей матрицы. Матрицы смежности обычно представляются двумерным массивом размера n x n, где n — число вершин графа.
Матрица смежности S — это квадратная матрица, в которой и число строк, и число столбцов равно n — числу вершин графа. В ячейки матрицы смежности записываются некоторые числа в зависимости от того, соединены соответствующие вершины рёбрами или нет, и от типа графа.
Списки инцидентности
Графы значительного объёма целесообразно хранить в памяти компьютера в форме списков инцидентности.
Список инцидентности одной вершины графа включает номера вершин, смежных с ней.
Ссылки на начало этих списков образуют одномерный массив, индексами которого служат номера вершин графа.
Преимущества и недостатки каждого способа.
Матрицы смежности целесообразнее использовать, когда:
- число вершин графа невелико;
- число рёбер графа относительно большое;
- в алгоритме часто требуется проверять, соединены ли между собой две вершины;
- в алгоритме используются фундаментальные понятия теории графов, например, связность графа.
Из-за последнего обстоятельства матрицы чаще используются в теоретических исследованиях графов.
Списки инцидентности целесообразнее использовать, когда:
- число вершин графа велико;
- число рёбер графа относительно невелико;
- граф формируется по какой-либо модели;
- во время действия алгоритма часто требуется модифицировать граф;
- в алгоритме часто используются локальные свойства вершин, например, окрестности вершин.
Итоги занятия.
Сегодня мы начали знакомиться с целым разделом математики и программирования – теорией графов. Разобрались, что такое граф, из чего он состоит, поговорили, какие бывают графы, и, самое главное, научились сохранять граф в памяти компьютера.
А на следующем занятии попробуем разобрать на логические болтики и винтики очень нужную в хозяйстве вещь — автомобильный навигатор!
Источник: teletype.in
Структуры данных: Графы II
Это вторая часть моей статьи о графах в серии статей о структурах данных. В первой части мы узнали о терминологии графов, типах графов и некоторых реальных применениях графовых структур данных. В этой части цикла мы рассмотрим представление графов, а также построим граф в коде Javascript.
Представление графов
Представление графов связано с тем, как графы могут быть записаны/реализованы в коде. Два наиболее распространенных способа представления графа — через список смежности или матрицу смежности
Список смежности
Список смежности очень прост: это список всех вершин со списком их ребер (смежных вершин). Список может быть любой линейной или итерируемой структурой данных (массивы, карты, связанные списки, очереди). Ниже приведены примеры графов, использующих список смежности.
Направленный граф

Неориентированный граф

Взвешенный граф

Плюсы
- При использовании на разреженных графах (графы с небольшим количеством ребер между вершинами) он занимает мало памяти.
- Его легко понять и реализовать.
- Он быстро создает и удаляет ребра и вершины.
Минусы
- Он менее эффективен по времени при проверке смежности вершин друг с другом.
Матрица смежности
Матрица смежности — это квадратная матрица, строки и столбцы которой равны количеству вершин в графе, а ребра представлены пересечениями между строками и столбцами. Ребра обозначаются цифрой 1, если они есть, и 0, если их нет. Взвешенные ребра обозначаются их весом. Ниже приведены примеры графов, использующих матрицу смежности.
Направленный граф

Неориентированный граф

Взвешенный граф

На приведенных выше изображениях видно, что пересечения AxA, BxB, CxC, DxD и ExE все равны 0; это потому, что в этих графах нет самопетли. Самопетля — это вершина в графе, которая указывает на саму себя.
Плюсы
- Очень экономит время при работе с плотными или полными графами (графы с большим количеством ребер между вершинами называются плотными, а графы со всеми возможными ребрами — полными).
Минусы
- Медленно создает и удаляет ребра и вершины.
- Он намного сложнее, чем список смежности.
- При использовании для разреженных графов (большинство графов являются разреженными) занимает мало памяти.
Реализация на Javascript
Вступление
Как оказалось тема алгоритмов интересна Хабра-сообществу. Поэтому я как и обещал, начну серию обзоров «классических» алгоритмов на графах.
Так как публика на Хабре разная, а тема интересна многим, я должен начать с нулевой части. В этой части я расскажу что такое граф, как он представлен в компьютере и зачем он используется. Заранее прошу прощения у тех кто это все уже прекрасно знает, но для того чтобы объяснять алгоритмы на графах, нужно сначала объяснить что такое граф. Без этого никак.
Основы
В математике, Граф — это абстрактное представление множества объектов и связей между ними. Графом называют пару (V, E) где V это множество вершин, а E множество пар, каждая из которых представляет собой связь (эти пары называют рёбрами).
Граф может быть ориентированным или неориентированным. В ориентированном графе, связи являются направленными (то есть пары в E являются упорядоченными, например пары (a, b) и (b, a) это две разные связи). В свою очередь в неориентированном графе, связи ненаправленные, и поэтому если существует связь (a, b) то значит что существует связь (b, a).
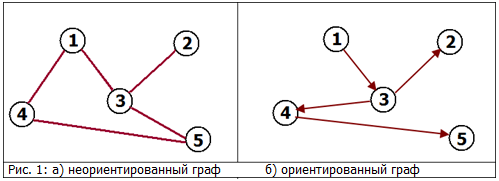
Неориентированный граф: Соседство (в жизни). Если (1) сосед (3), то (3) сосед (1). См рис. 1.а
Ориентированный граф: Ссылки. Сайт (1) может ссылаться на сайт (3), но совсем не обязательно (хотя возможно) что сайт (3) ссылается сайт (1). См рис. 1.б
Степень вершины может быть входящая и исходящая (для неориентированных графов входящая степень равна исходящей).
Входящая степень вершины v это количество ребер вида (i, v), то есть количество ребер которые «входят» в v.
Исходящая степень вершины v это количество ребер вида (v , i), то есть количество ребер которые «выходят» из v.
Это не совсем формальное определение (более формально определение через инцидентность), но оно вполне отражает суть
Путь в графе это конечная последовательность вершин, в которой каждые две вершины идущие подряд соединены ребром. Путь может быть ориентированным или неориентированным в зависимости от графа. На рис 1.а, путем является например последовательность [(1), (4), (5)] на рис 1.б, [(1), (3), (4), (5)].
У графов есть ещё много разных свойств (например они могут быть связными, двудольными, полными), но я не буду описывать все эти свойства сейчас, а в следующих частях когда эти понятия понадобятся нам.
Представление графов
Существует два способа представления графа, в виде списков смежности и в виде матрицы смежности. Оба способа подходят для представления ориентированных и неориентированных графов.
Матрица смежности
Этот способ является удобным для представления плотных графов, в которых количество рёбер (|E|) примерно равно количеству вершин в квадрате (|V| 2 ).
В данном представлении мы заполняем матрицу размером |V| x |V| следущим образом:
A[i][j] = 1 (Если существует ребро из i в j)
A[i][j] = 0 (Иначе)
Данный способ подходит для ориентированных и неориентированных графов. Для неориентированных графов матрица A является симметричной (то есть A[i][j] == A[j][i], т.к. если существует ребро между i и j, то оно является и ребром из i в j, и ребром из j в i). Благодаря этому свойству можно сократить почти в два раза использование памяти, храня элементы только в верхней части матрицы, над главной диагональю)
Понятно что с помощью данного способа представления, можно быстро проверить есть ли ребро между вершинами v и u, просто посмотрев в ячейку A[v][u].
С другой стороны этот способ очень громоздкий, так как требует O (|V| 2 ) памяти для хранения матрицы.
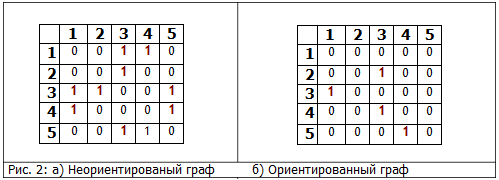
На рис. 2 приведены представления графов из рис. 1 с помощью матриц смежности.
Списки смежности
Данный способ представления больше подходит для разреженных графов, то есть графов у которых количество рёбер гораздо меньше чем количество вершин в квадрате (|E| В данном представлении используется массив Adj содержащий |V| списков. В каждом списке Adj[v] содержатся все вершины u, так что между v и u есть ребро. Память требуемая для представления равна O (|E| + |V|) что является лучшим показателем чем матрица смежности для разреженных графов.
Главный недостаток этого способа представления в том, что нет быстрого способа проверить существует ли ребро (u, v).
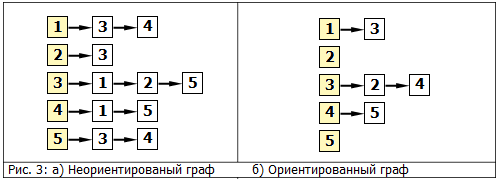
На рис. 3 приведены представления графов из рис. 1 с помощью списков смежности.
Применение
Те кто дочитал до этого места, наверное задали себе вопрос, а где же собственно я смогу применить графы. Как я и обещал я буду стараться приводить примеры. Самый первый пример который приходит в голову это социальная сеть. Вершинами графа являются люди, а ребрами отношения (дружба). Граф может быть неориентированным, то есть я могу дружить только с теми кто дружит со мной.
Либо ориентированным (как например в ЖЖ), где можно добавить человека в друзья, без того чтобы он добавлял вас. Если же он да добавит вас вы будете «взаимными друзьями». То есть будет существовать два ребра: (Он, Вы) и (Вы, Он)
Ещё одно из применений графа, которое я уже упоминал это ссылки с сайта на сайт. Представим Вы хотите сделать поисковую систему и хотите учесть на какие сайты есть больше ссылок (например сайт A), при этом учитывать сколько сайтов ссылается на сайт B, который ссылается на сайт A. У вас будет матрица смежности этих ссылок. Вы захотите ввести какую то систему подсчёта рейтинга, которая делает какие то подсчёты на этой матрице, ну, а дальше… это Google (точнее PageRank) =)
Заключение
Это небольшая часть теории которая понадобится нам чтобы для следующих частей. Надеюсь вам было понятно, а главное понравилось и заинтересовало читать дальнейшие части! Оставляйте свои отзывы и пожелания в комментариях.
В следующей части
BFS — Алгоритм поиска в ширину
Библиография
Кормен, Лайзерсон, Риверст, Штайн — Алгоритмы. Построение и анализ. Издательство Вильямс, 2007.
Словарь терминов теории графов
Граф — статья в английской Википедии
Статья это кросс-пост из моего блога — «Programing as is — записки программиста»
Источник: habr.com