В условиях применения сквозных компьютерных технологий, когда информация с компьютера передается непосредственно на станок по локальной сети, чертежи теряют свое ведущее положение, которое они занимали в традиционном проектировании. Тем не менее во всех машиностроительных САПР обычно имеются средства разработки чертежей и часто средства подготовки другой конст-рукторской документации (спецификаций и др.). Эти средства используются:
1) для создания дополнительного архива на бумажных носителях;
2) для передачи конструкторской документации на производство, где компьютерные технологии еще не применяются;
3) для обеспечения станочника наглядными материалами, позволяющими выполнять визуальный контроль процесса изготовления изделия.
В основе современного автоматизированного проектирования машиностроительных изделий лежит математически точное объемное геометрическое моделирование [6, 18]. Системы геометрического моделирования (наиболее развитые в CAD) позволяют создать информационную среду, подобную реальной среде, в которой создаются и изменяются физические модели. Они обеспечивают решение ряда проблем, связанных с использованием физических моделей в процессе проектирования (измерение, манипулирование) и позволяют рассматривать процесс проектирования как постепенную детализацию формы по мере развития идей разработчика. Кроме того, математически точные геометрические модели играют определяющую роль на всех последующих этапах жизненного цикла изделия, служат основой для оформления различной проектной документации.
Объём бетона и газоблока в SketchUp за 5 минут
Параметрическое моделирование (parametric modeling) заключается в том, что проектировщик определяет форму заданием геометрических ограничений и некоторых размерных параметров. Примерами ограничений являются параллельность двух граней, касательность двух линий и т.д. К размерной параметризации относят не только возможность свободного переназначения размеров формы (адаптивная параметризация), но и установление соотношений между размерами в виде математических уравнений (принудительная параметризация).
Системы геометрического моделирования делят на каркасные, поверхностные, твердотельные и гибридные (немногообразные).
В системах каркасного моделирования (wireframe modeling systems) форма объекта представляется в виде набора характеризующих ее линий и узловых точек. Соответствующее математическое описание каркасной модели представляет собой набор уравнений кривых, координат точек, условий принадлежности точек кривым и не содержит сведений о внешних поверхностях и объеме моделируемого объекта.
В системах поверхностного моделирования (surface modeling systems) математическое описание включает в себя не только сведения о ребрах и узлах, но и данные о поверхностях. Деталь, построенная методами поверхностного моделирования, представляется пустотелой оболочкой, состоящей из большого числа элементарных участков – патчей.
Патчи поверхности могут объединяться в одну поверхность или разбиваться на части. Из поверхности можно удалить часть ее патчей. В процессе модификации поверхности могут быть разрезаны, разбиты, сглажены, сопряжены, продлены. Считается, что методами поверхностного моделирования можно достоверно представить изделия сколь угодно сложной формы. Визуальная поверхностная модель объекта позволяет оценить эстетичность проекта, а математическое описание позволяет построить программу обработки детали на станке с ЧПУ (рисунок 2).
Проектирование кухни в SketchUp + EasyKitchen | Kitchen Design in SketchUp + EasyKitchen

Рисунок 2 – Моделирование обработки сложной
поверхности на станке с ЧПУ
Некоторые способы получения сложного контура поверхности:
· по вспомогательным пересекающимся или непересекающимся линиям;
· построение одной полилинией;
· построение в результате топологических операций;
· построение в результате применения к элементам преобразований (сдвиг, поворот, копирование массивом и т.д.).
Редактирование сложных контуров включает в себя следующие функции:
· добавление, удаление и изменение положения вершин контура;
· геометрическое перестроение сегментов контура (отсечение и дотягивание до указанных границ, удаление указанной части сегмента, рассечение в указанных точках и т.д.);
· геометрическое перестроение контура в целом (добавление или удаление отверстий, растягивание или сжатие в заданном направлении или масштабе, создание скруглений и фасок и т.д.).
Системы твердотельного моделирования (solid modeling systems) предназначены для работы с объектами, состоящими из замкнутого объема или монолита (solid). Твердое тело (solid-модель) характеризуется многогранным представлением и может быть отображено в виде прозрачного или непрозрачного объема, границы которого состоят из совокупности линий ребер и поверхностей граней. Математическое описание объекта, созданного в системе твердотельного моделирования, содержит сведения, по которым система может определить, где находится какая-либо точка: внутри объема, снаружи него или на его границе. Результаты твердотельного моделирования могут быть использованы:
· для контроля взаимного расположения деталей и работы механизма;
· для автоматизации подготовки конструкторской документации;
· для расчета инерционно-массовых характеристик изделия;
· для последующего проектирования обработки на станках с ЧПУ;
· для последующего моделирования условий нагружения в CAE-системе.
Функции моделирования, поддерживаемые большинством систем твердотельного моделирования, могут быть разделены на пять основных групп [6]:
1. Функции создания примитивов (primitive creation function) и булевские операторы (Boolean operations). Функции создания примитивов позволяют строить простейшие объекты (базовые тела, такие как параллелепипед, цилиндр, шар, конус, шар, клин, тор) указанием соответствующих значений их параметров.
Булевские операторы позволяют создавать так называемые составные тела путем комбинирования примитивов: твердотельные модели рассматриваются как множества точек, к которым применяются булевские операции теории множеств. Большинством систем твердотельного моде-лирования поддерживаются следующие булевские операции: сложение, вычитание и пересечение множеств. В итоге базовые тела образуют конструктивные элементы сложного тела. Таким образом, функции моделирования первой группы позволяют проектировщику быстро создавать форму, близкую к окончательной форме детали.
2. Функции создания объемных тел путем перемещения поверхностей. Обеспечивают создание тел сложной внешней формы кинематическим способом. Это так называемые функции заметания (swinging) и скиннинга (skinning). Функция заметания позволяет создавать объемное тело путем подъема (выдавливания, экструдии) или вращения некоторого профиля по заданному направлению. Функция скиннинга создает объемное тело, натягивая поверхность на заданные поперечные сечения.
3. Функции, предназначенные для редактирования существующей формы. Обычно это функции скругления (rounding), плавного сопряжения (blending) и лифтинга (lifting). Скругление или плавное сопряжение используется для модифицирования существующей модели, состоящей в замене острого ребра или вершины гладкой криволинейной поверхностью. Частный случай скругления с добавлением, а не удалением материала называется выкружкой (filleting). Лифтингом называется операция поднятия всей грани объемного тела или ее части в заданном направлении.
4. Функции моделирования границ (boundary modeling). Позволяют манипулировать вершинами, ребрами и гранями твердого тела. Данные операции аналогичны функциям систем поверхностного моделирования и служат в основном для создания сложных контуров заметания или скиннинга, а также изменения формы уже существующего тела. Например, перемещение вершины, замена прямого ребра криволинейным и т.п.
5. Функции объектно-ориентированного моделирования (feature-based modeling) или моделирования при помощи свободных форм. Позволяют создавать объемные тела, используя привычные элементы форм, получаемые в результате конкретного процесса производства. Таким образом, информация о методе построения контуров и тел в дальнейшем будет определять как способ внесения изменений в геометрическую модель изделия, так и проектирование технологии ее обработки, например, в процессе фрезерования. Однако к настоящему времени еще не создана программная среда, заранее определяющая методологию проектирования в зависимости от типа изделия.
Одной из важных характеристик твердого тела является история его создания. Содержательная часть истории создания включает описание всех элементов, используемых для построения тела, параметры и последовательность выполненных операций. История создания имеет иерархическую структуру.
На нижнем уровне размещаются геометрические примитивы (плоские или объемные), параметры примитивов. На всех последующих уровнях могут размещаться сборки тел, полученные в результате преобразования объектов нижнего уровня, а также промежуточные результаты топологических операций над отдельными конструктивными элементами. На верхнем уровне истории находится результирующее тело, например, деталь или сборка результирующих тел, например, узел или агрегат (рисунок 3).

Рисунок 3 – Сборочная модель вентиля и иерархия ее создания
Модификация модели зависит от способа ее построения и базируется на истории создания твердого тела. Основные правила модификации составного трехмерного тела:
· если при его построении использовались другие тела, то редактировать надо либо значения параметров конструктивных элементов, либо топологические операции;
· если при построении сложного тела использовались образующие линии, то редактировать необходимо геометрию этих линий.
Часто решающим фактором является умение конструктора использовать тот или иной метод редактирования.
Гибридные (немногообразные) системы моделирования (nonmanifold modeling system) позволяют использовать каркасные, поверхностные и твердотельные модели одновременно в одной и той же среде моделирования, расширяя диапазон доступных моделей сверх возможностей любой из упомянутых систем.
Источник: studopedia.su
ТЕХНОЛОГИИ, ИНЖИНИРИНГ, ИННОВАЦИИ
Измеритель диаметра, измеритель эксцентриситета, автоматизация, ГИС, моделирование, разработка программного обеспечения и электроники, БИМ

Геометрическое проектирование с помощью C3D Solver: экскурс профессионалов
Опубликовано 08.01.2017 автором kornelik

В статье описаны подходы, применяемые при разработке пользовательского инструментария для проектирования моделей и узлов с изменяемым взаимным положением и задания геометрических ограничений движения элементов и узлов. Вместе с тем разобрана классификация элементов и узлов по типу «трансляции» ограничений подчиненным объектам и по характеру ограничений. Задача была решена в САПР К3 с использованием параметрического ядра C3D Solver. C3D Solver дает возможность разработчикам программного обеспечения устанавливать зависимости между различными элементами геометрической модели.
Воспользуйтесь нашими услугами
- Наша продукция
- Презентации по направлениям
- Инжиниринг
- Консалтинг
- Металлообработка
- Моделирование
- Разработки
C3D Solver связывает элементы геометрической модели с помощью размеров и ограничений и обеспечивает сохранение заданных связей при изменении размеров, параметров модели, перемещении отдельных элементов модели или внесении иных изменений в геометрию модели.

Связи между объектами описываются геометрическими ограничениями, которые могут быть как размерными, задающими углы и расстояния, так и логическими, задающими совпадение, параллельность, перпендикулярность, касание. Геометрические ограничения могут накладываться на двумерные (2D) и трехмерные (3D) объекты.
Области применения C3D Solver:
- двумерные параметрические эскизы с управляющими размерами и ограничениями;
- позиционирование тел сборочной единицы с помощью сопряжений и размеров;
- перестроение модели с сохранением сопряжений после внесения изменений в модель;
- моделирование механизмов.
Постановка задачи
Одной из основных задач систем автоматизации проектных работ является решение геометрических задач, связанных с изменяемым взаимным положением узлов деталей и механизмов. Такого рода задачи обусловлены ужесточением требований, предъявляемых к модели конструкции. В рамках применения CALS-технологий необходимо свести к минимуму натурное создание опытных образцов и автоматизировать все этапы жизненного цикла изделий и конструкций [1]. Одним из этапов жизненного цикла изделий является не только геометрическое, но и кинематическое проектирование.
В общем случае, задача моделирования движения частей механизмов сводится к задаче удовлетворения ограничений, поскольку все основные кинематические связи выражаются через набор геометрических ограничений, таких как совпадение, соосность, параллельность, перпендикулярность и т. д. Каждая кинематическая пара из такой системы ограничений имеет свою относительную степень свободы. При этом отдельный узел считается условно неподвижным, а сочленяемые с ним – условно подвижными. Все соединения в совокупности с учетом, что детали конструкции не должны сталкиваться, оставляют каждой детали механизма определенные рамки движения, как например, диапазон возможного перемещения одной детали относительно другой, ограничение угла поворота при вращении одной детали относительно другой и пр.
Однако реальные объекты проектирования имеют существенно более сложную структуру, чем отдельные узлы или сочленения. Зачастую ограничения на движения тех или иных элементов конструкции определяются совокупностью узлов и механизмов. При этом на различных участках движения ограничения от одного из узлов оказывают более существенное влияние, чем ограничения от других узлов. На рисунке 1 приведен пример обычной мебельной дверки в закрытом положении, и в открытом положении. Этот пример показывает, что в каждой конкретной точке траектории движения на элементы накладываются ограничения свободного перемещения.
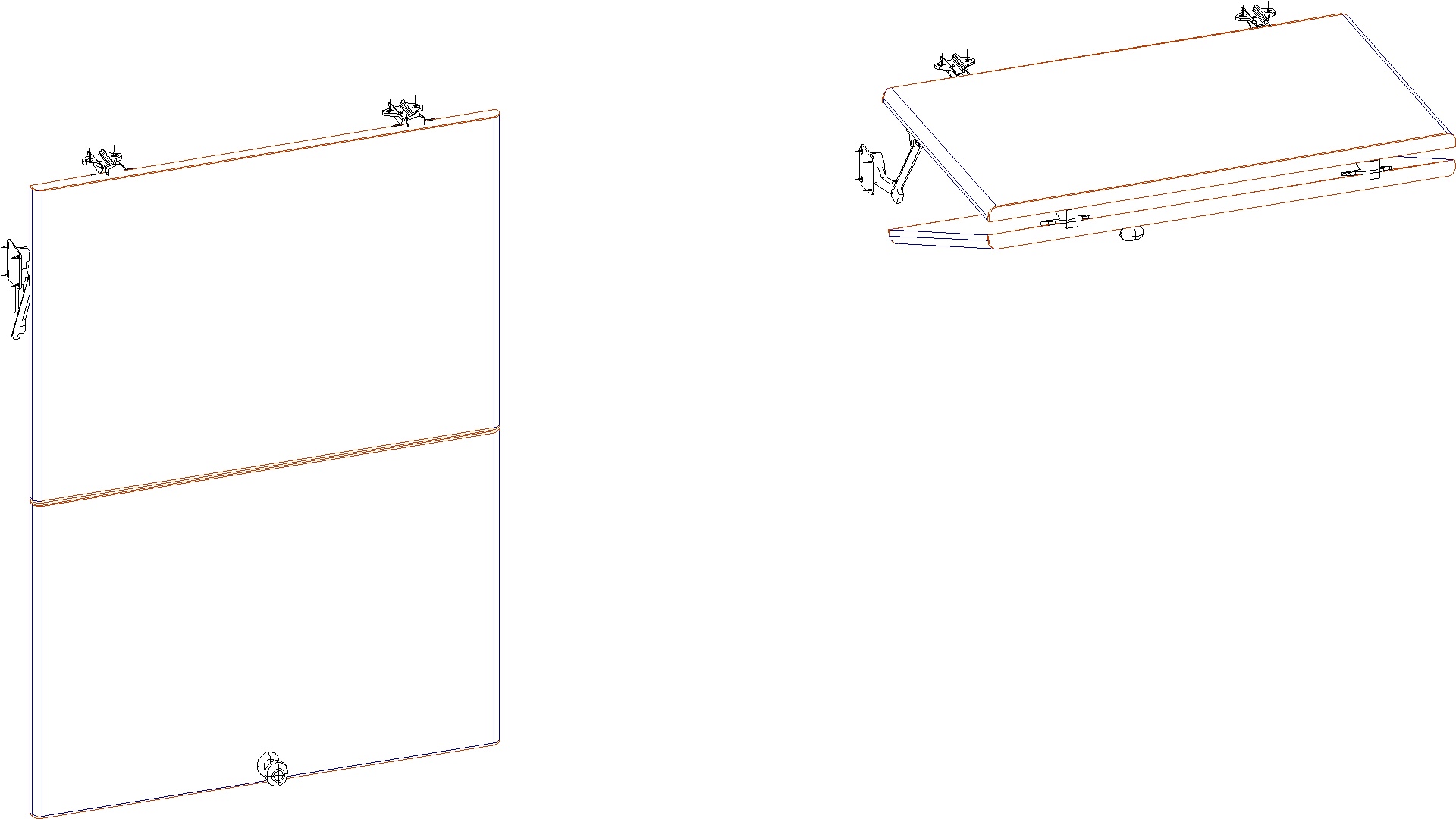
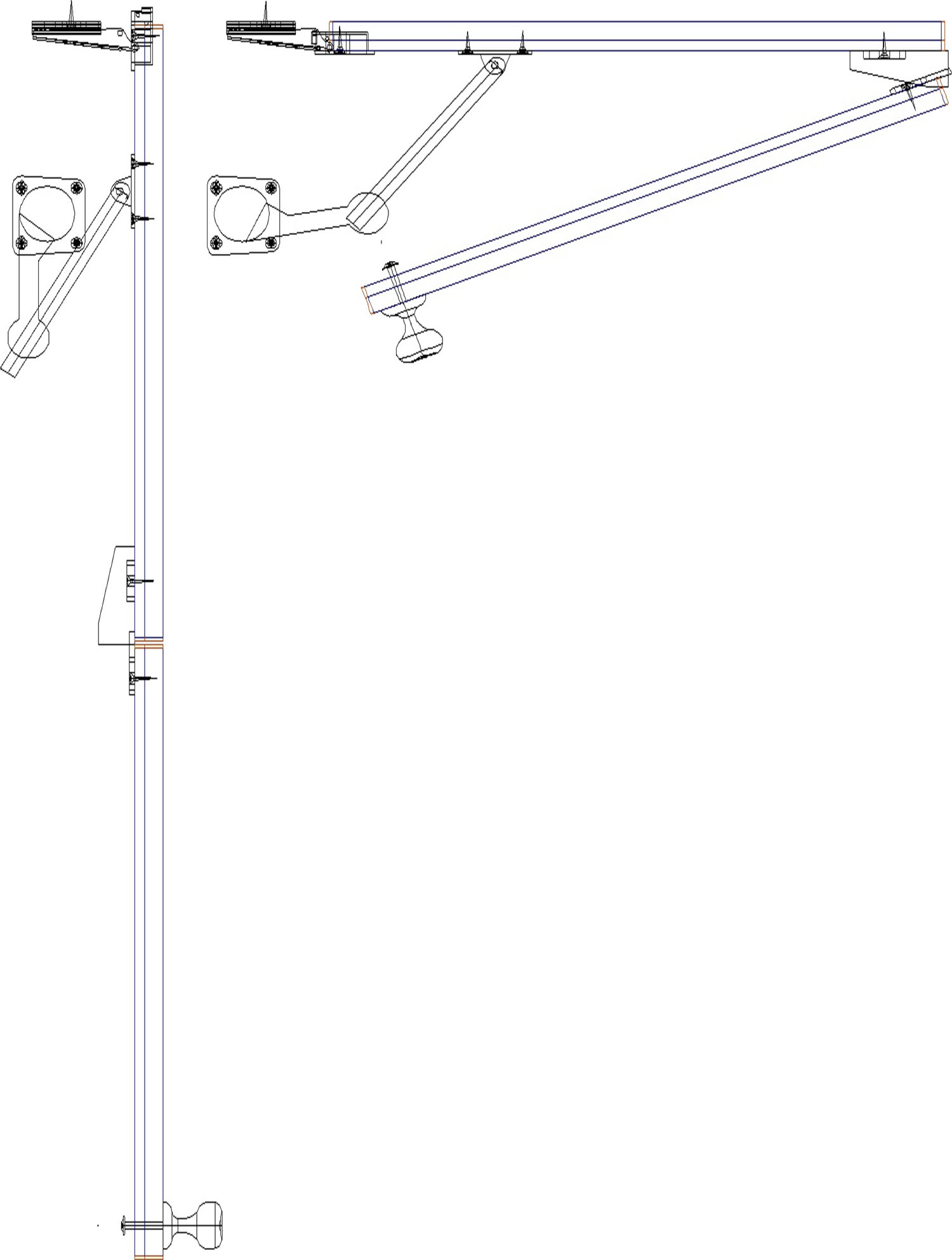
Рис. 1. Пример движения с ограничениями
Как видно, движение верхней створки дверки определяется двумя узлами – верхними петлями и подъемным механизмом. Причем, характер движения под влиянием каждого из механизмов в отдельности, не сводим к совокупному влиянию. Так, например, если бы не было петель на верхней створке, сама створка могла бы совершать любое плоскопараллельное движение, ограничиваемое только диапазоном выдвижного механизма подъемника. Ограничения на угол поворота подъемника не существует. Использование же только петель без подъемника не наложит ограничений на угол поворота (строго говоря, петли имеют ограничение на угол поворота, но этот угол обычно составляет не меньше 110 градусов, в то время как на рисунке угол отрывания меньше 90 градусов).
Что же касается нижней створки и ограничений в ее перемещении, то на нее оказывается гораздо более сложное влияние. На нее, помимо верхней створки, влияют петли, соединяющие створки.
Анализ существующих типовых кинематических улов и механизмов показал, что в подавляющем большинстве используются механизмы рычажного типа. Геометрические основы систем моделирования таких механизмов описаны в работе Турлапова В.Е. [2].
Классификация ограничений и объектов
В реальных сборочных конструкциях таких взаимоограничений может быть достаточно много. При этом положение объектов вычисляется не только в начальном и конечном положении, но и во всех промежуточных положениях тоже. Решить эту задачу в САПР К3 помогает параметрическое ядро C3D Solver, входящее в состав C3D Toolkit от компании C3D Labs [4].
Однако C3D Solver – это инструмент разработчика, а не конечного пользователя САПР. В системе К3 инструментарий решателя выведен на уровень пользователя. Задание ограничений на движение представляет собой запись информации в пользовательские атрибуты объектов.
Геометрические ограничения являются средством моделирования кинематических соединений. Например, шарнирное соединение, в котором участвует кинематическая пара дверной петли, оставляет подвижной части единственную степень свободы вращения. На языке ограничений такой механизм описывается двумя условиями – совпадение плоских граней и соосность цилиндрических граней. Таким образом, каждый узел механизма сообщает геометрическому решателю свое описание.
Ниже будет рассмотрена концепция моделирования, которая опирается на определенный порядок организации сборки, где одни узлы кинематической цепочки подчинены другим. Несмотря на иерархический характер сборки, C3D Solver может обрабатывать такие модели, как вариационные, где все детали, участвующие в системе ограничений, равноправны, что в частности позволяет решить обратную кинематическую задачу. Например, если приложить воздействие к дверной ручке, точно задав ей координаты в пространстве модели, можно вычислить положение остальных деталей сборки.
В САПР К3 объекты, подверженные влиянию ограничений на движение, делятся на три основных типа:
- Сам по себе объект, который сам в себе содержит ограничение и сам же их «отрабатывает»;
- Подчиненный объект – объект, который сам в себе информации о движении не содержит, а только лишь «отрабатывает» информацию, полученную извне;
- Главный объект – объект, который сам не движется, но содержит и передает информацию о движении подчиненным объектам.
Также в САПР К3 представлены элементарные типы кинематических ограничений. Более сложные ограничения представляют собой совокупность элементарных.
Так, в приведенном выше примере, объект «мебельная ручка» является подчиненным, поскольку сама ручка информацию о движении не содержит и только «отрабатывает» движение, полученное от других объектов. А объект «верхняя петля» (вернее, неподвижная часть петли) сама не движется, а «транслирует» информацию о движении другим объектам.
Также каждый объект, участвующий в перемещении, имеет следующие общие характеристики:
- Общее (для данного объекта) время начала движения;
- Общее (для данного объекта) время окончания движения;
- Направление движения времени (объект «открывается» или «закрывается);
- Количество «движений» – общее количество сдвигов и поворотов данного объекта.
Таким образом, каждый из объектов, участвующих в перемещении, может «присоединиться» к общему движению в тот или иной момент времени. При этом объект может совершать достаточно сложное движение из нескольких сдвигов и перемещений.

Рис. 2. Примеры кинематических ограничений
Решение поставленной задачи значительно упрощается при использовании параметрического подхода. В данном случае кинематические ограничения узлов нижних уровней формируют ограничения узлов верхних уровней структурного объекта. При этом использование механизмов репараметризации и депараметризации [3] позволяет динамически контролировать и вносить изменение в общую параметрическую модель объектов.
Математический аппарат
Положение каждого элемента и узла характеризуется его матрицей.
Существует три элементарных матричных преобразования – преобразование сдвига на вектор, преобразование поворота на угол, преобразование масштабирования. В нашем случае используются только преобразование сдвига и преобразование поворота.
C математической точки зрения, любое изделие представляет собой граф сборки [1], на который наложены параметрические связи [3] – см. рисунок 3.
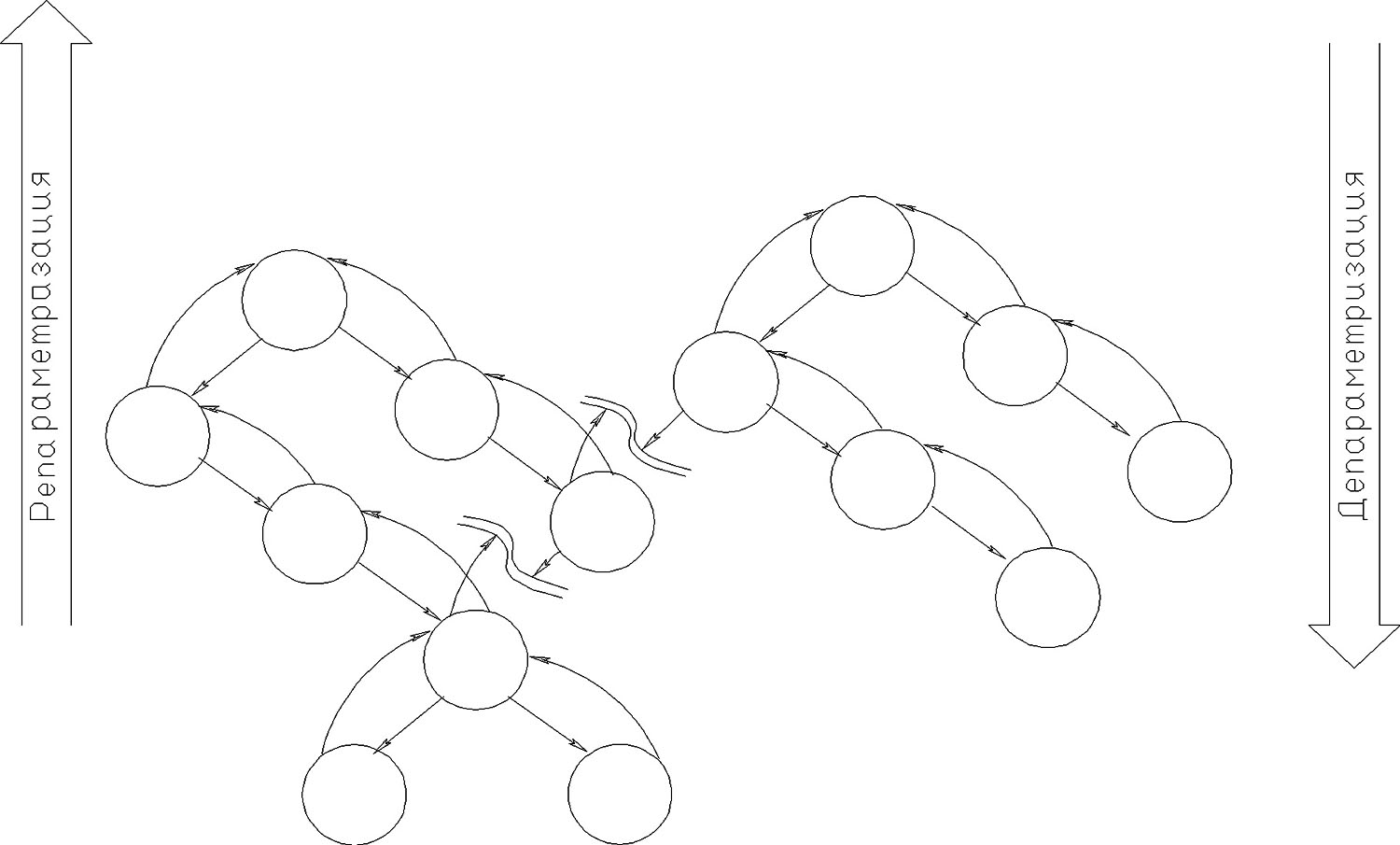
Рис. 3. Граф сборки модели
Данное утверждение целиком и полностью справедливо для формирования геометрии модели. В вершинах графа содержатся private и public параметры каждого отдельного узла.
Если же речь идет о формировании кинематической модели, то вершины графа также содержат набор кинематических ограничений и «транслируют» эти ограничения согласно концепции депараметризации и репараметризации. Ребра графа – это формирование матриц преобразования узлов более нижних уровней в зависимости от преобразования родительского узла и кинематических ограничений [2].
Изменение положения объекта – это, по сути, изменение его матрицы. С математической точки зрения, задача сводится и вычислению матрицы каждого из объектов.
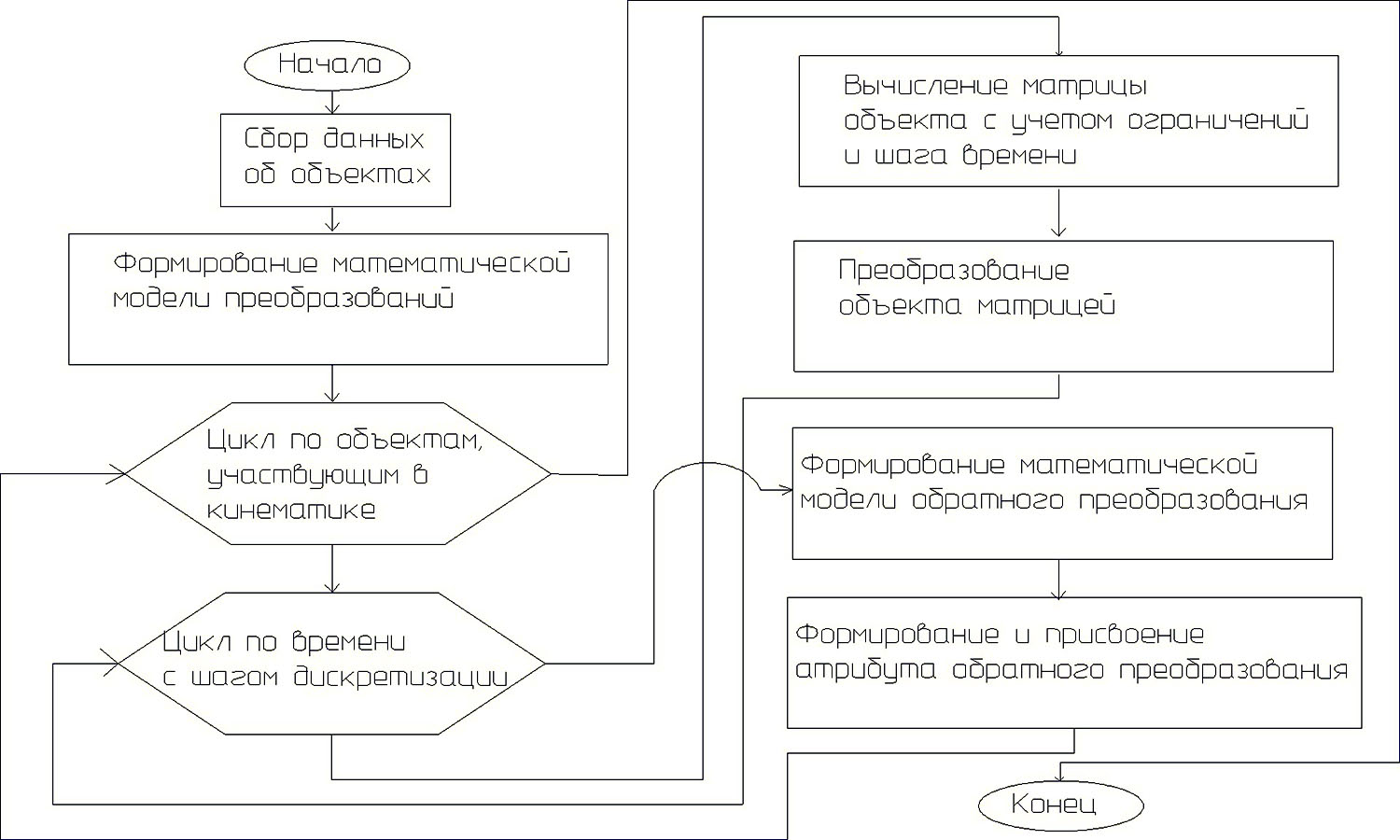
Рис. 4. Краткая блок-схема алгоритма
Стоит отдельно отметить, что задание таких элементарных движений в системе К3 доступно пользователю. Однако, на практике такое задание может показаться достаточно трудоемким. Плюс, дополнительную сложность создает то, в какой системе координат нужно осуществлять преобразование. Строго говоря, все преобразования должны выполняться в системе координат «родительского» объекта, поскольку детали и узлы перемещаются не относительно себя, а относительно более крупного узла, куда они входят. А вот задавать сами параметры удобней в системе координат узла…
С целью упрощения решения этих задач, разработчиками К3 написан алгоритм на макроязыке программы, которые производит преобразование параметров перемещения деталей и узлов из собственной локальной системы координат в систему координат родительского узла. Дополнительно к этому стоит отметить, что в САПР К3 разработчиками внесена достаточно большая библиотека типовых узлов и деталей с заданными ограничениями на движение элементов.
На практике при работе в САПР К3, конечному пользователю нет необходимости знать и понимать значение атрибута, содержащего информацию о перемещении того или иного объекта или его части. С точки зрения пользователя, в К3 реализован набор пользовательских функций, которые назначают, читают, изменяют возможные параметры движения объектов или узлов, накладывая ограничения на суммарное движение.
Выводы
В статье показано устройство модели САПР применительно к проектированию частей механизмов с изменяемым взаимным положением. Рассмотрено практическое применение модуля C3D Solver в САПР К3 моделирования сборочных конструкций и анализа их кинематики. Также разобрана классификация элементов и узлов по типу «трансляции» ограничений подчиненным объектам и по характеру ограничений. Показан пример использования методики для решения прикладной задачи, приведена классификация объектов по типу движения и по типу «трансляции» движения зависимым объектам.
Литература
1. Ротков С.И. Разработка средств геометрического моделирования и компьютерной графики пространственных объектов для CALS-технологий. Дисс. Докт. Техн.
Наук, Нижний Новгород, 05.01.01, ННГАСУ, 1999 год, 300 стр.
2. Турлапов В.Е. Геометрические основы систем моделирования кинематики пространствен-ных рычажных механизмов Дисс. Докт. Техн. Наук, М., МАИ,05.01.01, 2003 год, 280 стр.
3. Ермаков Е.С. Принципы многоуровневой параметризации при формировании объектов. Дисс. канд. Техн. наук, Ижевск, ИжГТУ, 05.13.12, 2008 г., 150 стр.
4. Сайт разработчика C3D Solver, компании C3D Labs.
Авторы: Е.Ермаков, Центр ГеоС, руководитель отдела; С.Митин, НИИМ ННГУ им. Н.И.Лобачевского, зав. лабораторией; С. Ротков, ННГАСУ, заведующий кафедрой инженерной геометрии, компьютерной графики и автоматизированного проектирования; А.Максименко, C3D Labs, руководитель разработки C3D Solver.
Воспользуйтесь нашими услугами
- Наша продукция
- Презентации по направлениям
- Инжиниринг
- Консалтинг
- Металлообработка
- Моделирование
- Разработки
Источник: integral-russia.ru
Обзор САПР на геометрическом ядре C3D
В предыдущих статьях о геометрическом ядре C3D мы разбирали его внутреннее устройство (структура ядра, модуль визуализации) и объясняли, чем оно отличается от API CAD-системы (статья). Проявить свои качества ядро, как инструмент разработчика САПР, может только в продуктах, написанных на его основе.
Сейчас на нашем ядре выпущено более 20 коммерческих и внутрикорпоративных САПР. В обзоре мы расскажем, что это за продукты, какую роль в них выполняет ядро и в чем особенности его применения. Многие продукты, упомянутые в обзоре, уже засветились на Хабре. Мы будем давать ссылки на статьи о них.
CAD/Проектирование
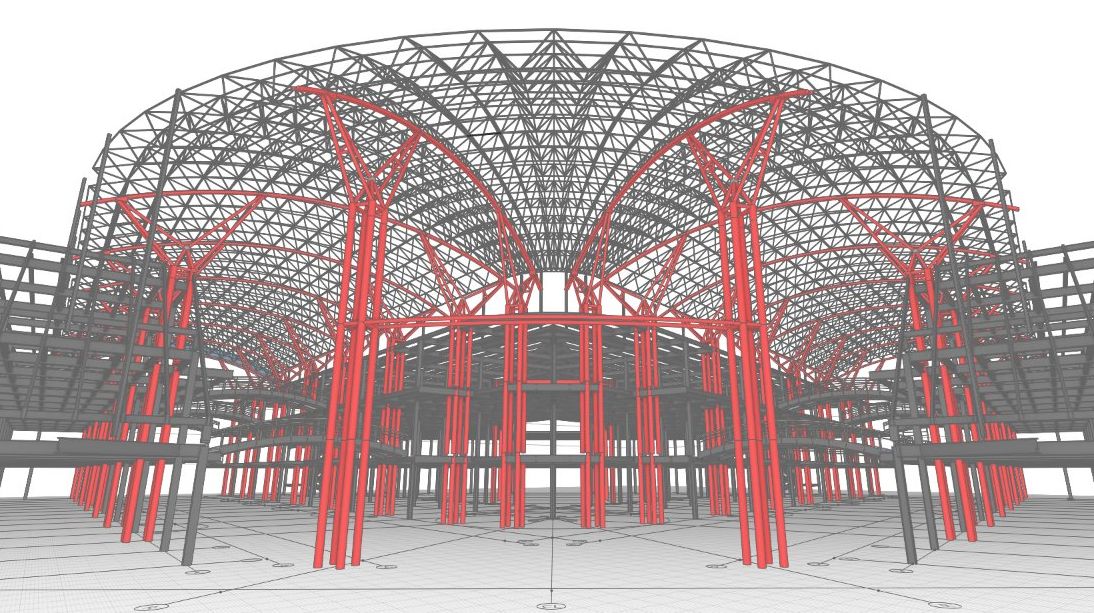
Первым мы всегда называем КОМПАС-3D, с которого, собственно, и началась история ядра. Сегодня с системой работают более 520 000 пользователей (с учетом коммерческих, домашних, учебных лицензий). В течение 12 лет ядро развивалось как внутренний компонент КОМПАС-3D и свою начальную функциональность получило из требований его разработчиков. Трехмерное моделирование было реализовано инструментами C3D Toolkit (геометрическое ядро, параметрический решатель, конвертеры), за исключением визуализации – 3D-движок появился у нас только два года назад. Сейчас КОМПАС-3D продолжает влиять на ядро: самые насущные задачи – это моделирование сложных форм и рост производительности.
В последней версии ядра C3D Modeler мы добавили новые частные случаи построения скругления и скругление трех граней. Вообще скругления остаются одной из самых сложных задач для геометрических ядер, т.к. охватить все варианты их построения невозможно.
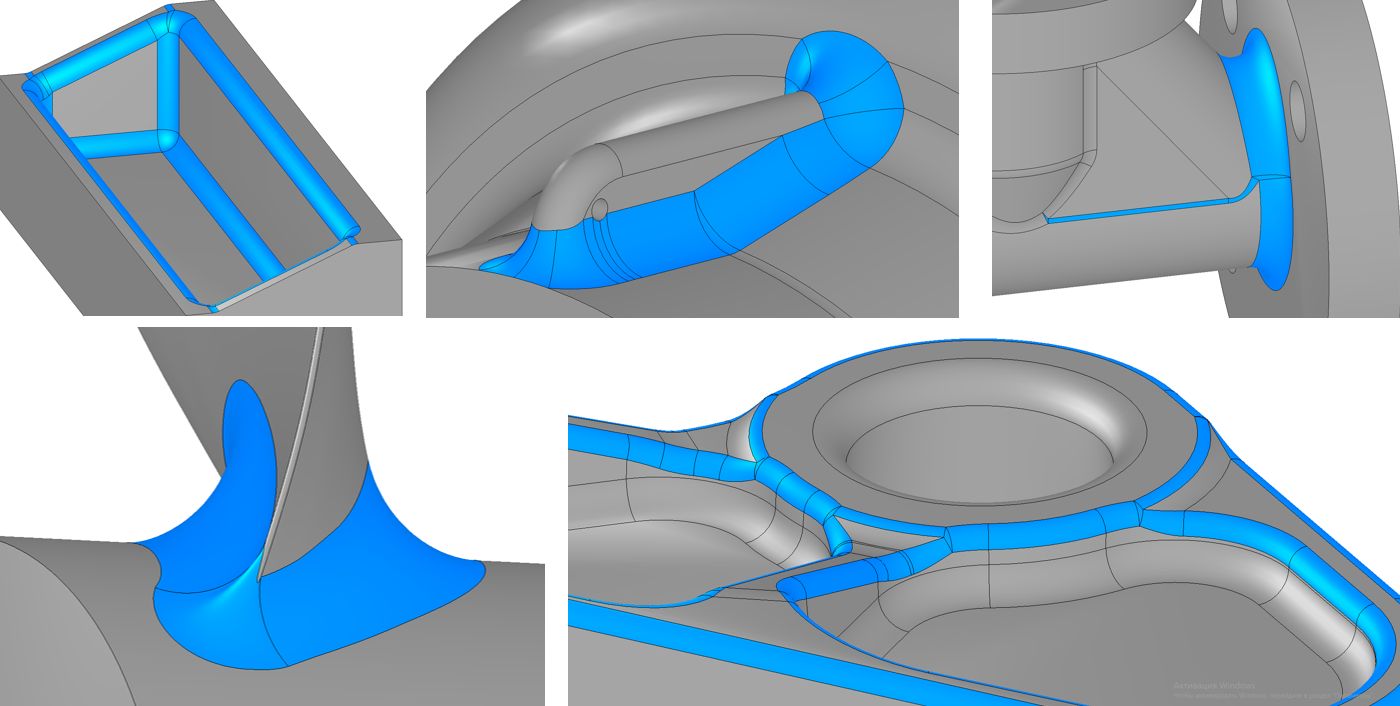
Частные случаи построения скругления
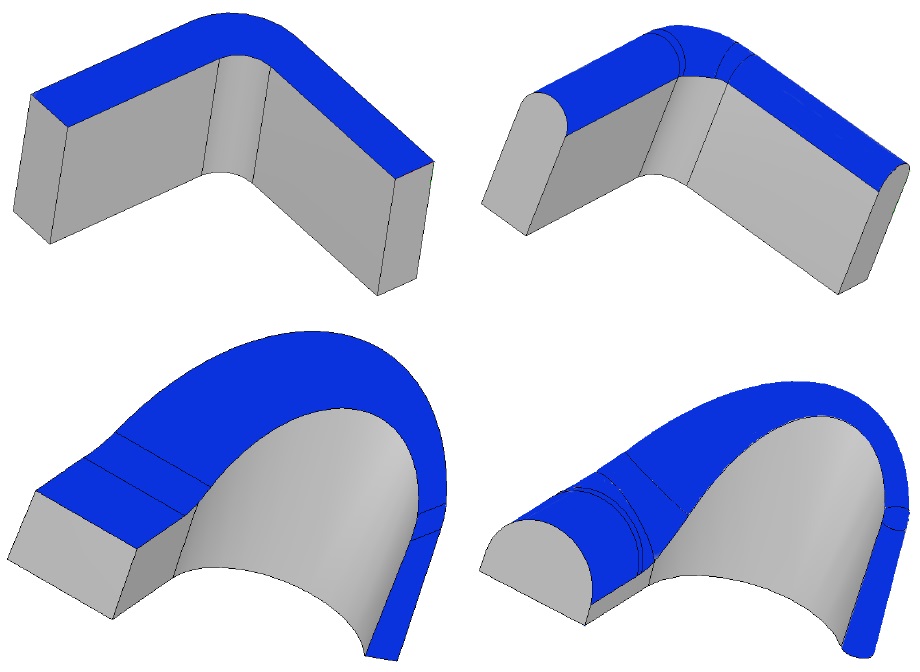
Скругление трех граней (или полное скругление)
Напрямую с геометрическим ядром работают и некоторые приложения КОМПАС-3D. В статье приведен пример приложения «Валы и механические передачи 3D», где с помощью ядра создаются точные модели элементов механических передач (конических, гипоидных и др.).
Еще одна хорошо известная САПР, в которой с недавних пор присутствует ядро C3D Modeler, это nanoCAD. В статье о новой платформе nanoCAD Plus 10 dows описал, как работает модуль 3D-моделирования: подключение геометрического ядра – C3D или ACIS – происходит по выбору пользователя, при этом наше ядро установлено по умолчанию.
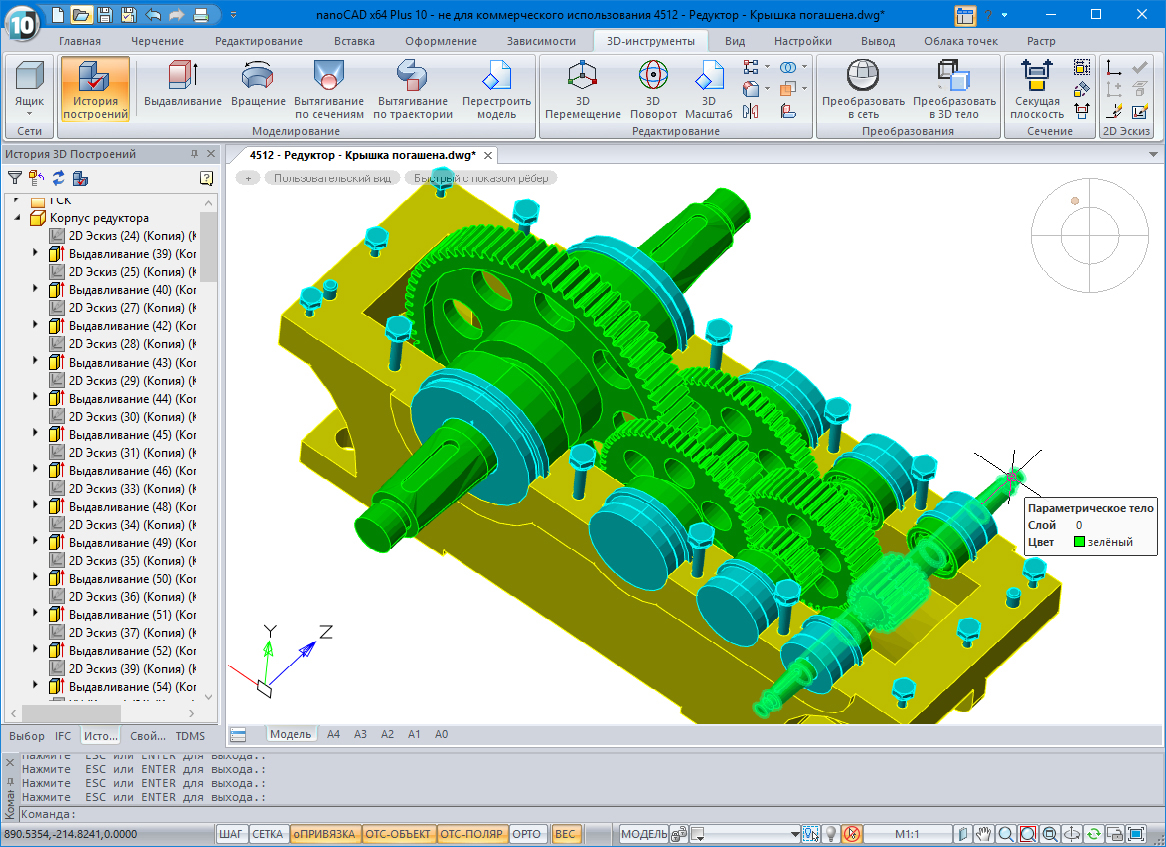
nanoCAD Plus с модулем 3D-моделирования на C3D
Чтобы перевести на C3D операции, которые раньше выполнялись на ACIS, потребовалось преодолеть не один барьер. Смена 3D-ядра влечет за собой изменение данных ассоциативных ссылок, изменение ориентации граней и ребер, изменение типа геометрии ребер, изменение топологии тела при построении, изменение топологии тела при смене формата 3D-модели, отклонения геометрии сложных поверхностей. Все это разработчики «Нанософт» сумели победить.
EDA/Проектирование электроники
Если механические САПР перешли к парадигме трехмерного проектирования довольно давно, то для САПР электронных устройств 3D становится мейнстримом только сейчас. Мировые и российские разработчики находятся здесь примерно в равных позициях с точки зрения возможностей своих продуктов. И что приятно для нас – и те, и другие работают с нашим ядром.
Год назад компания Altium, разработчик популярного во всем мире Altium Designer (преемника P-CAD), лицензировала C3D Toolkit, и в ближайшее время должна выйти новая версия Altium Designer, в которой 3D-моделирование выполнено уже нашими инструментами.
Параллельно с Altium российская компания «Эремекс» разрабатывает систему проектирования печатных плат Delta Design, опираясь на геометрическое ядро C3D Modeler.

Модель печатной платы в Delta Design
Для Delta Design нам пришлось решать проблему визуализации печатных плат с большим количеством слоев и компонентов – ускорять в ядре операции с регионами.
CAE/Инженерный анализ и расчеты
Инженерам-проектировщикам промышленных объектов хорошо знакома компания «НТП Трубопровод» и ее продукты СТАРТ, ПАССАТ, Штуцер-МКЭ. С 2014 года в программе ПАССАТ, выполняющей прочностные расчеты сосудов и аппаратов, на ядре C3D Modeler создаются все элементы 3D-модели, а это довольно большой список: цилиндрические обечайки и конические переходы, приварные днища и отъемные крышки, укрепление отверстий, врезки в обечайки и выпуклые днища, фланцевые соединения и т.д.
Ядро также отвечает за расчет геометрических характеристик (объем, площадь поверхности, центр тяжести, момент инерции), а конвертеры C3D Converter – за экспорт моделей в форматы ACIS, IGES, Parasolid и STEP.

ПАССАТ
В этом году «НТП Трубопровод» подключил ядро к своему второму продукту Штуцер-МКЭ (расчеты на прочность узлов врезки в оборудование), но пока не для всех геометрических операций. Из-за особенностей моделей возникли сложности с булевыми операциями и проекцией кривых на поверхность. В основном, в нашем ядре Штуцер-МКЭ хранит кривые и строит скругления.
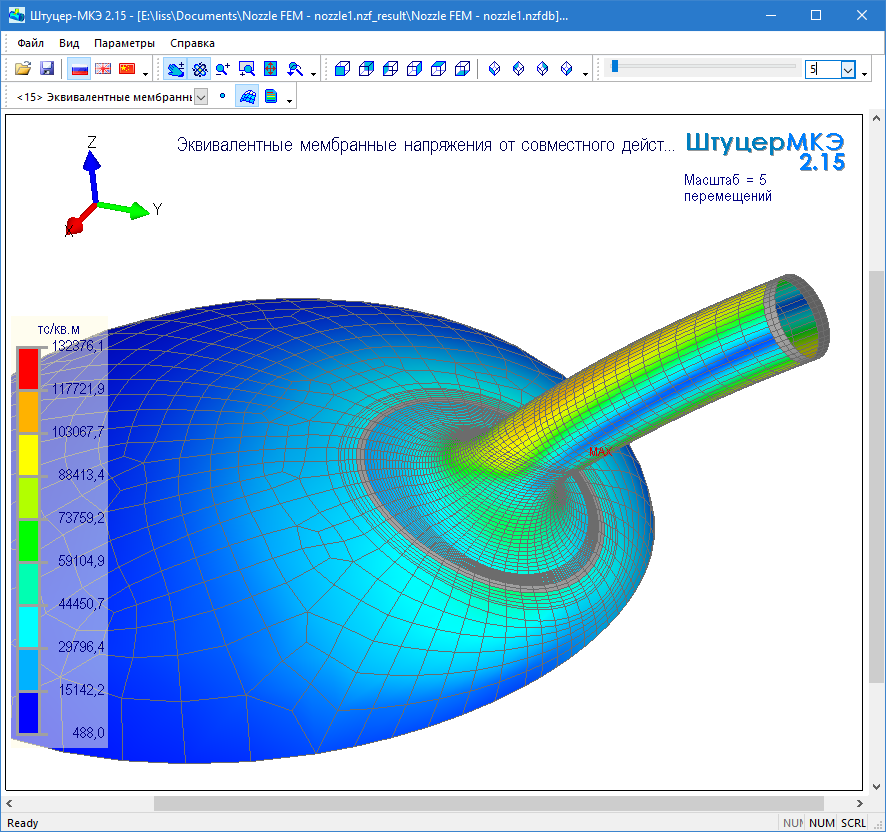
Штуцер-МКЭ
В разработке расчетного ПО использует ядро C3D и ядерный центр РФЯЦ-ВНИИТФ Госкорпорации «Росатом». О назначении продукта мы рассказывать не имеем права, но несколько скриншотов показать можно.
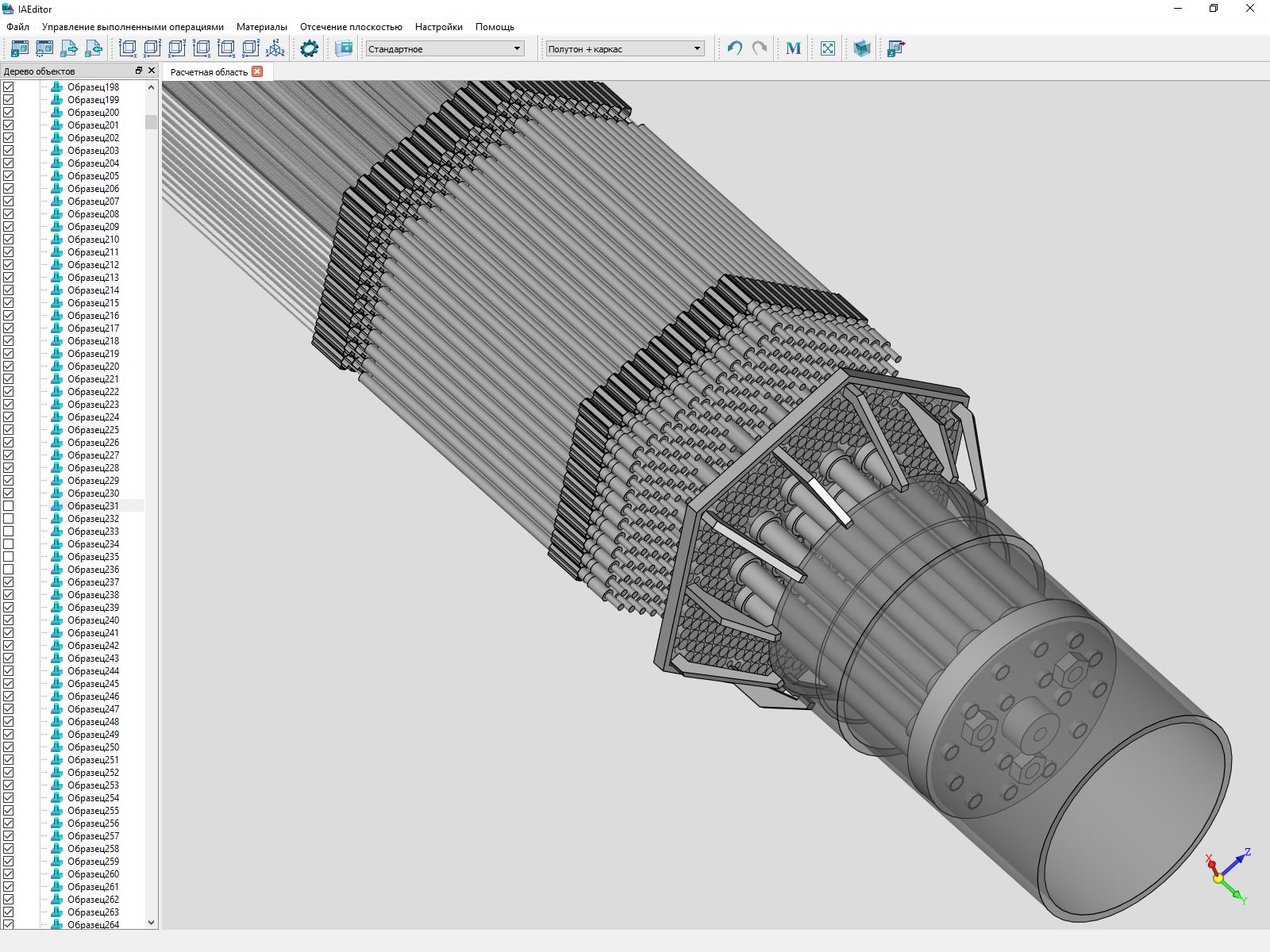
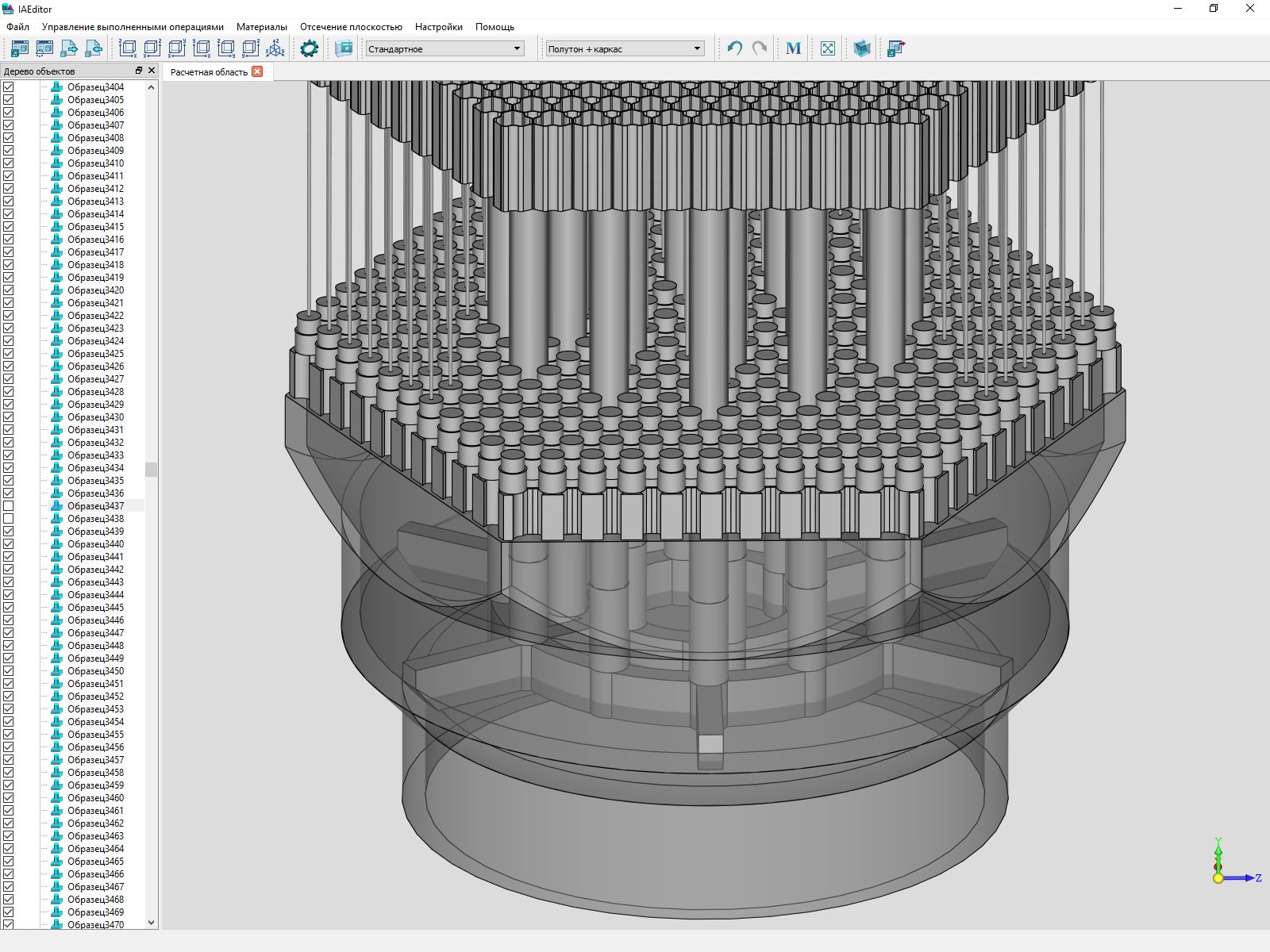
Сначала наши компоненты использовались в этом продукте только для моделирования геометрии и импортаэкспорта готовой геометрии через обменные форматы, а визуализацию разработчики делали на собственных компонентах. Но год назад они перешли на наш движок C3D Vision. По их оценке, улучшилось качество и возросла скорость вывода элементов сцены. Теперь от нас ждут инструментов для создания, вывода и работы с 2D-сценой.
AECCloud/Мобильные и облачные приложения
Среди наших заказчиков пока мало приверженцев облачных технологий, но если они решатся зайти на эту дорогу, то такой опыт у нас тоже есть.
Например, на ядре C3D Modeler реализован КОМПАС:24, Android-просмотрщик моделей КОМПАС-3D (статья ).
Новосибирская компания ЛЕДАС интегрировала ядро со своей облачной платформой LEDAS Cloud Platform (LCP). Платформа переносит САПР-приложения в web-среду и предоставляет в браузере функции хранения и управления данными, визуализации, навигации, коммуникации и совместной работы.
По запросу одного американского заказчика мы сделали параметрический решатель C3D Solver для JavaScript. Продукт, написанный на его основе, может не только функционировать в браузере, но и производить геометрические расчеты на стороне клиента. Насколько мы знаем, подобного решения нет ни у одного разработчика в мире.
PDM/Управление инженерными данными
Для удобства работы и обмена информацией в PDM-системах формируется вторичное представление документов (копия в нейтральном формате). Для этого могут использоваться VRML, eDrawings, 3D PDF. Разработчики ЛОЦМАН:PLM за 15 лет попробовали разные варианты и в прошлом году остановились на нашем просмотрщике C3D Viewer (статья). Он позволяет просматривать 3D-модели и выполнять аннотирование.
Кстати функционал аннотирования был разработан по заказу команды ЛОЦМАН:PLM и входит в платную Enterprise-версию продукта. Базовый C3D Viewer остается бесплатным (скачать его можно здесь).
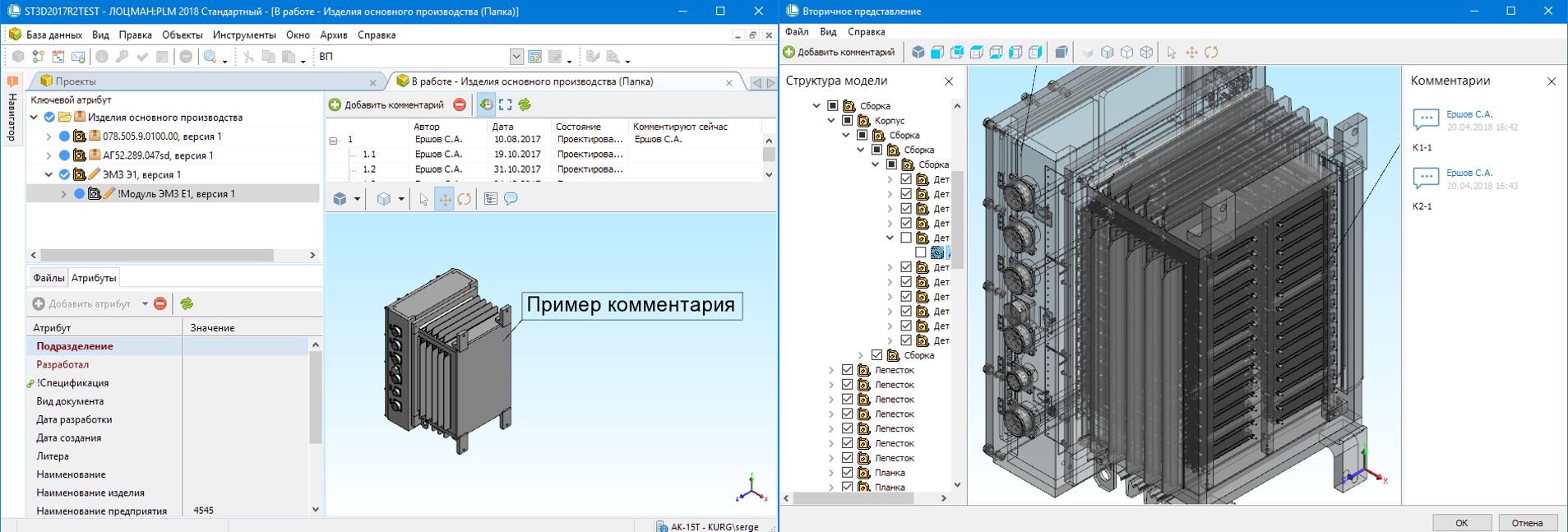
Вторичное представление в ЛОЦМАН:PLM
CAM/Производство
Обычно в системах подготовки управляющих программ для станков с ЧПУ геометрическое ядро играет важную, но не ключевую роль: оно работает в препроцессоре, обеспечивая импорт геометрической модели из CAD-систем и доработку геометрии перед программированием обработки. По сути, ядро нужно для насыщения CAM-систем CAD-функционалом, востребованным технологами. Не обойтись без 3D-ядра и разработчикам интегрированных CAD/CAM решений.
В Мордовском государственном университете давно сложилась команда по CAM-направлению. Сначала они написали «Модуль ЧПУ. Токарная обработка» на API КОМПАС, а позднее – «Модуль ЧПУ. Фрезерная обработка» для 2,5 и 3-координатной обработки непосредственно на ядре C3D. Их путь отличается от традиционного подхода CAM-разработчиков к ядру.
Приложение интегрировано в рабочее пространство КОМПАС-3D и использует CAD-модель, созданную в КОМПАС, в качестве источника геометрической информации. С помощью функций C3D моделируются пространственные области удаления материала, их вычитание из заготовки, построение трехмерных траекторий. Специфика применения C3D для задач CAM состоит в том, что такие сложные операции геометрического моделирования, как построение оболочек, нахождение кривых пересечения, булевы операции, не являются конечными объектами моделирования (как в системах CAD), а являются элементарными кирпичиками для реализации высокоуровневых алгоритмов, специфичных для области CAM. Это накладывает дополнительные требования к согласованию точности результатов, полученных через ядро, с общей точностью вычислений в рамках высокоуровневых задач.
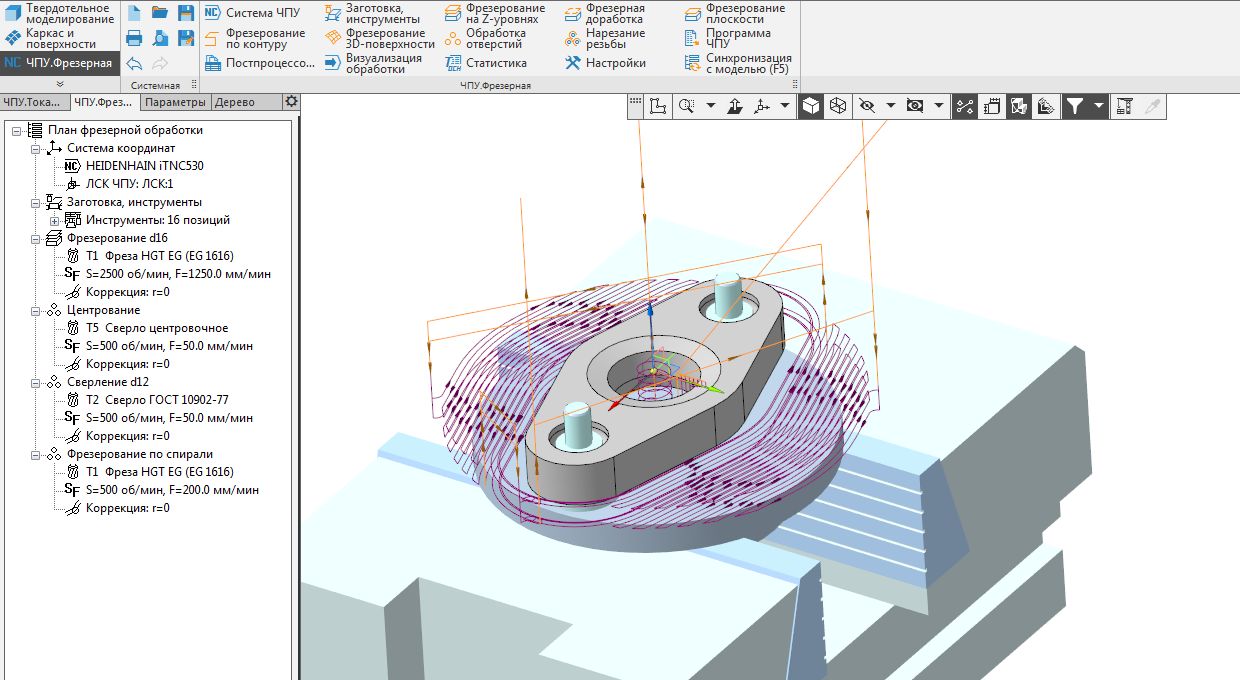
Модуль ЧПУ. Фрезерная обработка
Заинтересованные разработчики могут самостоятельно протестировать C3D Toolkit. Все компоненты предоставляются бесплатно на три месяца, с документацией, по заявке на нашем сайте.
- Блог компании АСКОН
- CAD/CAM
Источник: habr.com