О параметрах-переменных часто говорят, что подпрограмма возвращает их значения, подчеркивая тем самым, что они являются или могут являться выходными данными некоторого вычислительного процесса.
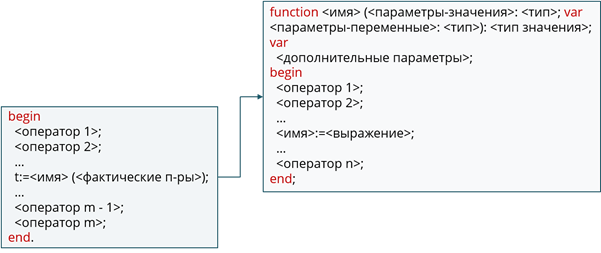
Распространены подпрограммы, требующие возврата всего одного выходного параметра, являющегося скаляром (то есть, единственным значением, а не вектором или матрицей). В этих случаях вместо подпрограммы-процедуры используется подпрограмма-функция, возвращающая скалярный результат своей работы в основную программу. Поэтому для функции в ее заголовке необходимо указать тип возвращаемого результата, а в теле функции должен присутствовать хотя бы один оператор присваивания, в левой части которого записывается имя функции:
(Список формальных параметров) :
var описания локальных переменных;
Здесь Выражение1 должно иметь тот же тип, что и указанный в заголовке ТипРезультата, а оператор Имя:=Выражение1; не обязан быть последним в теле функции. Поскольку результат выполнения функции возвращается в основную программу через ее имя, то обращение к функции записывается аналогично стандартным функциям в виде операнда-выражения, стоящего справа от знака присваивания:
35 Функции (def) в Python. Определение и вызов функции
Выражение2 может состоять только из вызова функции вида Имя (список фактических параметров) или включать этот вызов как часть более сложного выражения., переменная Результат должна соответствовать типу функции. В записи выражения должны быть соблюдены все изученные ранее правила соответствия типов.
Все, сказанное выше о согласовании формальных и фактических параметров, а также о параметрах-значениях и переменных, в полной мере относится и к функциям.
Фактически, стандартные подпрограммы Паскаля также делятся на функции и процедуры, в зависимости от способа их вызова. Так, writeln относится к стандартным процедурам, а sin — к функциям. Правда, некоторые из стандартных подпрограмм имеют переменное число параметров, что запрещено пользовательским подпрограммам.
Формально при использовании функций не запрещено возвращать более одного значения через дополнительные параметры-переменные, подобные тем, что мы изучили для процедур. Можно сказать, что функции в Паскале — это процедуры, способные возвращать дополнительное скалярное значение. Во многих других языках программирования специального разделения на процедуры и функции нет.
Чтобы окончательно уяснить не-синтаксические различия между функциями и процедурами, обобщим их в табл. 18.2.
Табл. 18.2. Различия между процедурами и функциями
| Процедура | Функция |
| Вызывается отдельным оператором | Вызывается из выражения справа от знака присваивания |
| Использует параметры-значения и переменные | Использует параметры-значения и переменные, дополнительно доступен параметр-переменная с именем, совпадающим с именем функции |
Напишем и вызовем простейшую функцию, находящую максимальный из двух своих вещественных аргументов:
Python. Команды print() input()
if a>b them max:=a
Вызвать эту функцию мы могли бы различными способами:
С помощью функции вычислили максимальное из значений x, y и записали его в переменную r.
Максимальное из значений x, y, z записали в переменную t.
Последний вызов иллюстрирует, что, как и стандартные функции, функции, написанные программистом, могут вызываться из сколь угодно сложных выражений — при условии, что будут соблюдаться правила соответствия параметров. Написанную нами функцию max нетрудно было бы реализовать и в виде процедуры:
procedure max (a,b:real; var c:real);
Однако, при вызове этой процедуры постоянно пришлось бы передавать «лишний» параметр c, служащий только для хранения возвращаемого значения.
3.4.2. Функции
Понятие функции в языке Бейсик близко знакомому вам понятию функции в математике. Определим функцию одного аргумента.
ИмяФункции (Аргументфункции)
ИмяФункции — это имя либо уже имеющейся в языке (встроенной) функции, либо функции, определяемой программистом. В первом случае — это служебное слово языка. Во втором случае имя строится по правилам, которые ничем не отличаются от правил построения имени переменной.
АргументФункции — это либо число, либо переменная, либо выражение (арифметическое, строковое, логическое).
В информатике говорят, что функция возвращает своё значение, если задано значение её аргумента. Это означает, что в системе есть специальная программа, которая вычисляет значение этой функции.
Аналогично функции одного аргумента можно определить и функцию нескольких аргументов.
Синтаксис функции нескольких аргументов таков:
ИмяФункции (СписокАргументовФункции)
Аргументы в СпискеАргументовФункции отделяются друг от друга запятой.
Встроенные функции бывают нескольких видов. Математические функции в Visuа1 Ваsiс есть набор встроенных математических функций. Наиболее распространённые из них:
Аbs(х) – абсолютная величина числа х;
CInt(х) – целое число, ближайшее к числу х;
Cos(х) – косинус числа х;
Fix(х) – целое число, равное числу х без дробной части;
Int(х) – наибольшее целое число, не превышающее х;
Sin(х) – синус числа х;
Sqr(x) – квадратный корень из числа х;
Log(x) – логарифм натуральный числа x , и т. д.
Где может возникнуть потребность в таких функциях, как Int(х) и ей подобных? Приведём один из примеров использования этой функции.
Пусть решается такая задача. Трое студентов сообща заработали определённую сумму денег S и хотят честно (поровну) разделить эту сумму. Очевидно, что каждый из них должен получить сумму S1, равную S/3. Пусть эта элементарная задача — часть более серьёзной задачи, которая решается на компьютере. Будет получен такой, например, результат: S1 = 233.3333333.
рублей.
Очевидно, что результат желательно округлить так, чтобы он сохранял только два знака после запятой (ведь речь идёт о рублях, а меньше сотой доли рубля значения не бывает). При этом используется такой приём:
S2 = Iпt(S1 * 100)/100,
где S1 — неокруглённый результат; S2 — результат с указанным округлением.
Финансовых функций в Visuа1 Ваsiс больше десятка. Приведём пример только одной из них. Это функция, которая решает задачу о банковском кредите. Её синтаксис следующий:
Ртt(ПроцСтавка, ЧислоПлатежей, СуммаКредита).
Она возвращает размер разового (например, ежемесячного) платежа (со знаком минус), если известны: Процентная Ставка, общее Число Платежей (например, число месяцев) и Сумма Кредита.
Системные функции. К системным функциям относятся функции, действие которых напрямую зависит от работы системы Visuа1 Ваsiс. К таким функциям относятся две:
– функция InputВох — для ввода данных пользователем через системное окно;
Источник: studfile.net
Вспомогательные алгоритмы и подпрограммы: функции
В этом видеоуроке учащиеся продолжат рассматривать подпрограммы в языке Паскаль и познакомятся с понятием функции, узнают, для чего они применяются и как описываются в программировании. Будут рассмотрены локальные и глобальные параметры подпрограмм.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет.
Получите невероятные возможности
1. Откройте доступ ко всем видеоурокам комплекта.
2. Раздавайте видеоуроки в личные кабинеты ученикам.
3. Смотрите статистику просмотра видеоуроков учениками.
Получить доступ
Конспект урока «Вспомогательные алгоритмы и подпрограммы: функции»
· Описание и вызов функций.
· Применение функций при написании программ.
Функцией называется подпрограмма, которая при выполнении принимает на вход любое количество параметров, а по завершении работы возвращает одно значение заданного типа, содержащееся в переменной, название которой совпадает с названием функции.
В программах на языке Pascal, функции, как и процедуры, описываются в разделе описания подпрограмм. Описание функции начинается со служебного слова function. После него, через пробел, следует имя функции, которое не должно совпадать с именем программы или с именами переменных.
После него через пробел в скобках следует описание формальных параметров, которые оформляются, как и в процедуре. Сначала через запятую перечисляются параметры-значения одного типа. Через двоеточие после них указывается тип параметров. Параметры разных типов разделяются точкой с запятой. Дальше со служебного слова var начинается описание параметров-переменных.
Они описываются также, как и параметры-значения. После описания формальных параметров через двоеточие указывается тип значения, возвращаемого функцией. После него следует точка с запятой. На следующей строке, если нужны дополнительные переменные, следует раздел описания промежуточных параметров функции. Дальше, между логическими скобками, следует блок операторов функции.
После служебного слова end следует точка с запятой.
Важно: в программном блоке функции, переменной, название которой соответствует названию функции, хотя бы один раз должно быть присвоено какое-либо значение.
Так же, как и процедура, функция может не иметь формальных параметров, если все входные данные задаются через глобальные параметры.
Вызов функции в операторном блоке программы происходит лишь в составе какого-либо оператора. При этом указывается имя функции, после которого, в скобках, следуют её фактические параметры. При вызове функции, также как и в случае с процедурой, важно чтобы количество, порядок следования и тип её фактических параметров совпадали с формальными параметрами в её описании.
При выполнении программы, в которой содержится функция, выполняются сначала операторы, следующие до содержащего вызов функции. При выполнении этого оператора вычисляется значение функции. Для этого фактические параметры, указанные при вызове, подставляются на места формальных параметров, указанных в описании функции.
После этого выполняются операторы, содержащиеся в её операторном блоке. Так как в операторном блоке функции, переменной соответствующей функции присваивается какое-либо значение, это значение подставляется в оператор содержащий вызов функции. После чего его выполнение завершается и начинают выполняться операторы, следующие в теле программы после него.
Принцип работы вызова функции
Задача: Написать программу, которая определяет является ли целое n, заданное пользователем, простым числом Мерсенна. 4 ≤ n ≤ 2 000 000 000.
Числами Мерсенна называются числа вида 2 p – 1. Числа Мерсенна названы так в честь французского математика Марена Мерсенна, который изучал эти числа. Он также являлся учителем Блеза Паскаля, в честь которого назван изучаемый нами язык программирования.
Простыми числами Мерсенна называются числа Мерсенна, которые являются простыми и у которых p – также простое число. Простым называется число, которое не делится нацело ни на одно число кроме единицы и себя самого.
Данную задачу можно разделить на две подзадачи: в начале определим является ли заданное n числом Мерсенна. Если это число Мерсенна – определим является ли оно простым. Однако первую подзадачу можно также разбить на две подзадачи.
Сначала мы должны определить, можно ли представить число n + 1 в виде 2 p . Если число можно представить в указанной форме, то нам остаётся определить не делится ли n на какое-нибудь число кроме 1 и себя самого. Для решения этой подзадачи мы опишем логическую функцию prost. Для решения первой подзадачи мы опишем логическую функцию, которую назовём Mersenn.
Начнём написание программы для решения этой задачи. Назовём её число Мерсенна. Для решения задачи нам понадобится переменная для хранения числа n. По условию задачи, это число будет принимать значение на промежутке от 4 до 2 000 000 000, поэтому зададим его принадлежащим к целочисленному типу integer. Запишем логические скобки.
Тело программы будет начинаться с оператора writeln, выводящего на экран сообщение о том, что это программа, определяющая, является ли целое n простым числом Мерсена. Дальше будет следовать оператор write с запросом на ввод n и оператор readln для его считывания.
Для определения истинности высказывания о том, является ли n числом Мерсена, мы позже опишем логическую функцию Mersenn. Поэтому сейчас запишем условный оператор, условием которого будет значение этой функции, с параметром n. После служебного слова then в нём будет следовать ещё один условный оператор, который будет проверять, является ли n простым числом.
Для определения истинности высказывания об этом мы позже опишем логическую функцию prost. В качестве условия укажем её значение также с параметром n. В этом условном операторе, после слова then запишем оператор write, который выводит на экран сообщение о том, что заданное n является простым числом Мерсенна.
После служебного слова else запишем такой же оператор вывода, выводящий сообщение о том, что заданное n не является простым числом Мерсенна. Запишем служебное слово else для внешнего условного оператора. После него будет следовать такой же оператор вывода, как и предыдущий, поэтому просто скопируем его. На этом мы завершили описание основной программы.
program chislo_Mersenna;
writeln (‘Программа, определяющая, является ли целое n простым числом Мерсенна.’);
if Mersenn (n)
then if prost (n)
then write (n, ‘ является простым числом Мерсенна.’)
else write (n, ‘ не является простым числом Мерсенна.’)
else write (n, ‘ не является простым числом Мерсенна.’);
Теперь опишем функцию определения истинности высказывания о том, что n является числом Мерсенна. Как мы помним, мы назвали её Mersenn, и она будет иметь один формальный параметр, назовём его также n. Как и в основной программе оно будет целочисленного типа integer.
Так же нам потребуется промежуточная переменная p, которая будет хранить степень двойки в указанном представлении числа n, поэтому для её хранения нам будет достаточно целочисленного типа byte. Напишем логические скобки. Сначала для удобства расчёта p увеличим значение n на 1. Присвоим переменной p значение ноль, так как мы её ещё не рассчитывали.
Затем запишем оператор цикла с предусловием while. Его условием будет: n mod 2 = 0. В самом цикле мы будем значение переменной p увеличивать на 1, а n делить без остатка на 2. Таким образом, по окончании работы цикла, если n будет равно единице, то его удалось представить в виде 2 p , в противном случае этого сделать нельзя.
Запишем условный оператор, который проверяет равно ли n единице, если это так – присвоим переменной Mersenn значение true. В противном случае запишем оператор присваивания переменной Mersenn значения false. На этом описание функции Mersenn будет завершено.
function Mersenn (n: integer): boolean;
while n mod 2=0 do
then Mersenn:=true
else Mersenn:=false;
Теперь разберёмся, как определить является ли целое число n простым. Так как простым является число, которое не делится ни на одно целое число кроме 1 и себя самого, нам достаточно проверить делимость числа n на все числа на промежутке от 2 до n – 1. Но этот промежуток можно сократить. Очевидно, что
n = * ,
следовательно, если при разложении n на два множителя один из них будет больше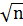 
, то второй будет меньше его. Значит нам достаточно проверить делимость n на все числа до 
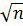. Так же мы можем, единожды проверив делимость n на 2, больше не проверять его делимость на чётные числа, так как если хотя бы один из делителей числа является чётным, то и само число должно быть чётным. И наконец, если мы нашли хотя бы один делитель числа Эн проверку можно остановить.
Опишем логическую функцию проверки того, является ли число n простым. Мы назвали функцию prost. Так как функция Mersenn содержит вызов функции prost, то она должна находится выше. У неё будет всего один аргумент – число n. Как и в основной программе зададим его принадлежащим к типу integer.
Сама же функция будет логического типа boolean. Так же нам понадобится промежуточная переменная, в которой бы будем перебирать множители, назовём её i. Она так же будет принадлежать к типу integer, и ещё одна промежуточная логическая переменная – t. Запишем операторный блок функции.
Он будет начинаться с того, что мы проверим не делится ли n без остатка на 2 и результат присвоим переменной t. Так как мы проверили делимость n на 2 – присвоим переменной i значение следующего предполагаемого делителя, то есть 3. Дальше запишем оператор цикла с предусловием while с условием продолжения работы: i sqrt (n).
Так как функция извлечения квадратного корня sqrt является вещественной, то при расчёте результата возможна погрешность, поэтому добавим к sqrt (n) единицу. Второй частью условия продолжения работы цикла будет то, что t = true, то есть что мы ещё не нашли ни одного делителя n. В теле цикла будет больше одного оператора, поэтому напишем логические скобки.
В цикле мы сначала запишем условный оператор с условием: n mod i = 0. Если это условие выполняется, то i является делителем n, а значит n не является простым числом и мы присвоим переменной t значение false. После проверки мы увеличим значение i на 2, чтобы пропустить чётное число, и перейти сразу к следующему за ним нечётному числу.
Таким образом по завершении работы цикла переменная t будет содержать значение истинности высказывания о том, что число n является простым. Присвоим это значение переменной функции prost. На этом работа функции будет завершена.
function prost (n: integer): boolean;
t:=n mod 2<>0;
if n mod i=0
Источник: videouroki.net