2. «Интерфейс» функции описан в ее заголовке функции. В нем имеется имя функции, по которому она известна далее в программе, формальные (входные) параметры и результат.
3. Имя функции -идентификатор.
4. Результат функции — это выходная переменная, которую формирует функция и значение которой используется затем в том месте программы, где она вызывается. Результат, как любая другая переменная, должен быть определенного типа. В данном случае -вещественное число -минимальный элемент массива. Сразу огорчим: массив не может быть результатом функции, только простые переменные.
5. После имени функции в круглых скобках идет список формальных параметров, разделенных запятыми. Формальные параметры -это тоже переменные особого рода, что видно из заголовка -их синтаксис в перечислении напоминает определение обычных переменных. Как и все другие переменные они имеют тип и могут быть обычными переменными и массивами. Формальные параметры содержат входные данные функции, передаваемые при ее вызове и могут использоваться только самой функцией в процессе ее работы.
[C++ Урок 1] Структура программы
6. Вслед за заголовком идет тело функции -нечто, заключенное в фигурные скобки. Тело функции -это и есть выполняемое функцией законченное действие (алгоритм), представленное в виде операторов и операций над переменными.
7. После открывающейся скобки в теле функции присутствуют определения локальных переменных. Это переменные, которые «известны» только данной функции и являются ее собственностью. Более того, они создаются в памяти при входе в тело функции и исчезают при выходе. Локальными переменными пользуется функция при необходимости иметь собственные данные.
Fore kc .ru
Рефераты, дипломы, курсовые, выпускные и квалификационные работы, диссертации, учебники, учебные пособия, лекции, методические пособия и рекомендации, программы и курсы обучения, публикации из профильных изданий
Источник: www.matrikclab.ru
Презентация на тему Тема Функции и структура программы Лекция 23.09.13г. 1
Лекция 23.09.13г.Функции и модульность программыМодульность в языках программирования — принцип, согласно которому программное средство (ПС) – программа, библиотека, web-приложение и др. разделяется на отдельные сущности, называемые модулями. Модульность позволяет упростить задачи
- Главная
- Разное
- Тема Функции и структура программы Лекция 23.09.13г. 1
Слайды и текст этой презентации
Слайд 1Тема
Функции и структура программы
Лекция 23.09.13г.

Слайд 2Лекция 23.09.13г.
Функции и модульность программы
Модульность в языках программирования — принцип,
согласно которому программное средство (ПС) – программа, библиотека, web-приложение и
др. разделяется на отдельные сущности, называемые модулями. Модульность позволяет упростить задачи проектирования ПС и распределения процесса разработки ПС между группами разработчиков, а также позволяет реализовать методологию повторного использования кода.
Python 3. Архитектура программ. Работа с пакетами(модулями)
При разбиении ПС на модули для каждого модуля указывается реализуемая им функциональность, а также связи с другими модулями. Роль модулей могут играть структуры данных, библиотеки функций, классы, сервисы и другие программные единицы, реализующие некоторую функциональность и предоставляющие интерфейс к ней.
В языке С модульность поддерживается функциями, препроцессоными командами, многофайловой структурой программы и заголовочными файлами.

Слайд 3Лекция 23.09.13г.
Функции и модульность программы
Функции разбивают большие вычислительные задачи на
более мелкие и позволяют инкапсулировать («упрятать» в оболочку) детали реализации
некоторой функциональности, предоставив пользователям («клиентам») формат обращения к этой функциональности (интерфейс). Это делает программу в целом более ясной и облегчает внесение в нее изменений.
Пример: функция, преобразующая символьное изображение числа, записанное в строке, в само число.
//atoi_.c
#include
int atoi_(char s[]) int i, n, sign;
for (i = 0; isspace(s[i]); i++) ;
sign = (s[i] == ‘-‘) ? -1 : 1;
if (s[i] == ‘+’ || s[i] == ‘-‘)
i++;
for (n = 0; isdigit(s[i]); i++)
n = 10 * n + (s[i] — ‘0’);
return sign * n;
>
//Ex025.c
#include
#include
int atoi_(char[]);
int main() int n = atoi_(» -347ab»);
printf(«n = %dn», n);
system(«PAUSE»);
return 0;
>

Слайд 4Лекция 23.09.13г.
Определение функции
Для того, чтобы использовать функцию, ее необходимо определить,
т.е. описать её интерфейс (объяснить, как функцией можно воспользоваться) и
привести программный код, раскрывающий, как функция работает (записать реализацию функции на языке программирования).
Определение любой функции имеет следующую форму:
тип_возвращ_знач имя_функции(список_объявлений_арг) объявления и операторы
>
Различные части этого определения могут отсутствовать, но обязательными являются: имя_функции, пара круглых скобок и пара фигурных скобок, т.е. «минимальная» функция определяется так: fun()<> Это – «пустышка», которая не принимает никаких аргументов и ничего не делает (имеет пустое «тело»). Подобные функции могут использоваться в качестве «заглушек» при разработке программ.
Если при объявлении функции не указан тип возвращаемого значения, то по умолчанию подразумевается тип int.

Слайд 5Лекция 23.09.13г.
Функции и программы
Любая программа является набором определений
типов,
переменных
и
функций.
Функции обмениваются данными посредством передачи аргументов и возвращения
значений, а также через внешние переменные.
Функции могут следовать друг за другом в файле исходного кода в любом порядке, и текст программы можно разбивать на любое количество файлов, но при этом запрещается разбивать текст функции между файлами.
Функция не может быть определена внутри другой функции
В результате своей работы функция может возвратить в вызывающую ее функцию результат – некоторое значение, тип которого объявлен перед именем функции. Для этого в теле функции должен присутствовать хотя бы один оператор возврата вида: return выражение; Вызывающая функция может игнорировать (т.е. не использовать) возвращаемое значение.
Существует еще одна форма оператора возврата: return; В этом случае в вызывающую функцию ничего не передается, а при определении функции в качестве типа возвращаемого значения указывается void.
Тело функции может не содержать оператора возврата return ; при этом возврат из функции происходит при достижении конца блока (закрывающей скобки > ).

Слайд 6Лекция 23.09.13г.
Аргументы передаются по значению
Все аргументы в функцию передаются по
значению, т.е. функция получает значения своих аргументов в виде временных
переменных, а не оригиналов. Следовательно, все действия функции со своими аргументами никак не отражаются на переменных, переданных функции при вызове. Исправить это положение можно с помощью указателей.
Пример: функция, производящая «обмен значениями» двух переменных.
//Ex026_err.c – Err.
#include
#include
void swap(int a, int b) int c = a;
a = b; b = c;
>
int main() int x = 5, y = 7;
printf(«x = %d, y = %dn»,x,y);
swap(x, y);
printf(«x = %d, y = %dn»,x,y);
system(«PAUSE»);
return 0;
>
//Ex026_ok.c – Ok.
#include
#include
void swap(int *a, int *b) int c = *a;
*a = *b; *b = c;
>
int main() int x = 5, y = 7;
printf(«x = %d, y = %dn»,x,y);
swap(y);
printf(«x = %d, y = %dn»,x,y);
system(«PAUSE»);
return 0;
>

Слайд 7Лекция 23.09.13г.
Функция main
Программа может использовать любое количество функций при одном
условии: в программе обязательно должна присутствовать в точности одна функция
с именем main («главная» функция), т.к. запуск программы на выполнение операционной системой производится всегда через эту функцию (т.е. main начинает выполняться первой).
Функция main всегда имеет тип возвращаемого значения int, через это значение ОС уведомляется об успешности или не успешности завершения программы (т.н. «код завершения»). А т.к. int подразумевается «по умолчанию», то тип возвращаемого значения для main часто не указывают.
Существует две формы main:
без аргументов – main() и
с аргументами – main(int argc, char *argv[])
Вторая форма main позволяет при вызове программы из командной строки передать в нее произвольное количество строковых аргументов (об этом позже).

Слайд 8Лекция 23.09.13г.
Пример программы с модульной структурой
Разработать программу нахождения корня нелинейного
уравнения f(x)=0 методом деления отрезка пополам:
Даны: отрезок [a, b], на
котором предположительно находится корень; точность определения нуля функции – epsy и точность определения корня – epsx.

Слайд 9Лекция 23.09.13г.
Программа нахождения корня
//Ex020_2013.c — корень нелинейного уравнения
#include
#include
#include
double fun(double x) < return cos(x); >
double bisec(double a, double
Слайд 10Лекция 23.09.13г.
Создание отдельных модулей
Разместим каждую из функций – fun() и
bisec() в отдельных файлах и создадим для них заголовочные (интерфейсные)
// fun.c
#include
double fun(double x) return cos(x);
>

Слайд 11Лекция 23.09.13г.
Создание отдельных модулей
// bisec.c
#include
#include
#include
#include «fun.h» //
подключение модуля
double bisec(double a, double b, double epsx, double epsy)
Слайд 12Лекция 23.09.13г.
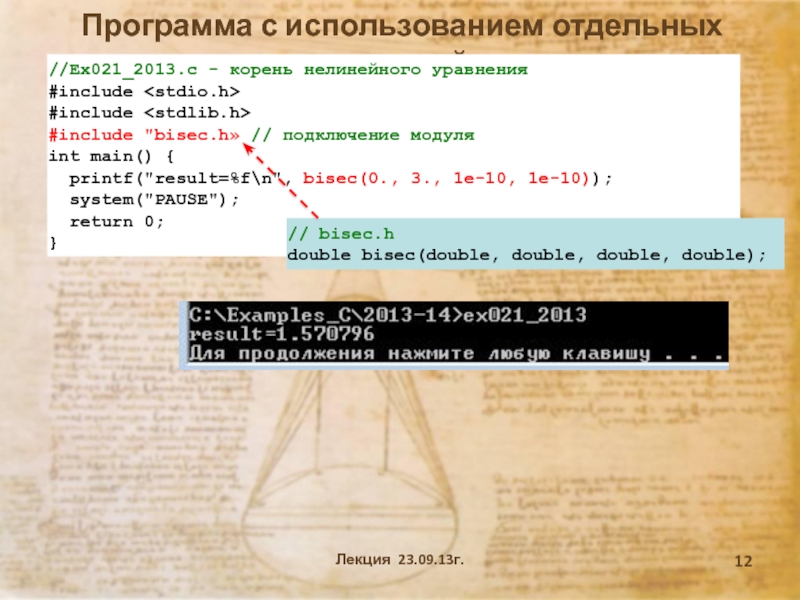
Программа с использованием отдельных модулей
//Ex021_2013.c — корень нелинейного уравнения
#include
#include
#include «bisec.h» // подключение модуля
int main() printf(«result=%fn», bisec(0.,
3., 1e-10, 1e-10));
system(«PAUSE»);
return 0;
>
// bisec.h
double bisec(double, double, double, double);
Слайд 13Лекция 23.09.13г.
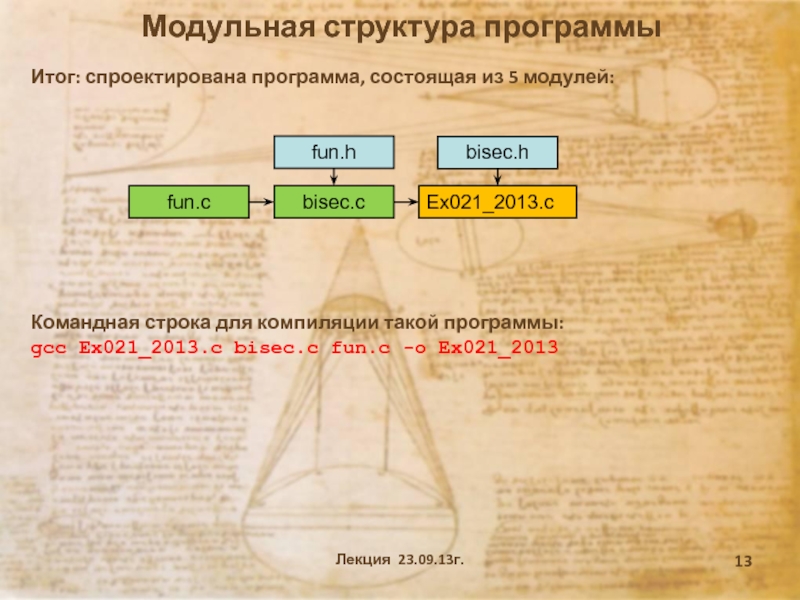
Модульная структура программы
Итог: спроектирована программа, состоящая из 5 модулей:
bisec.h
Ex021_2013.c
bisec.c
fun.c
Командная
строка для компиляции такой программы:
gcc Ex021_2013.c bisec.c fun.c -o Ex021_2013
fun.h
Слайд 14Лекция 23.09.13г.
Рекурсия
Рекурсия — процесс повторения чего-либо самоподобным способом. Например, вложенные
отражения, производимые двумя точно параллельными друг другу зеркалами, являются одной
из форм бесконечной рекурсии.
Наиболее общее применение рекурсия находит в математике и информатике. Здесь она является методом определения функций, при котором определяемая функция применена в теле своего же собственного определения. При этом бесконечный набор случаев (значений функции) описывается с помощью конечного выражения, которое для некоторых случаев может ссылаться на другие случаи, если при этом не возникает циклов или бесконечной цепи ссылок. Фактически это способ определения множества объектов через самого себя с использованием ранее заданных частных определений.

Слайд 15Лекция 23.09.13г.
Примеры рекурсии в математике
Факториал целого неотрицательного числа n определяется
так :
n! = n * (n-1)! , 0! = 1.
Числа
Фибоначчи: Fn = Fn-1 + Fn-2, F1 = F2 = 1.
Практически все геометрические фракталы задаются в форме бесконечной рекурсии, например, треугольник Серпинского:

Слайд 16Лекция 23.09.13г.
Рекурсия в программировании
В программировании рекурсия — вызов функции из
неё же самой, непосредственно (простая рекурсия) или через другие функции
(сложная или косвенная рекурсия), например, функция A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.
Преимущество рекурсивного определения объекта заключается в том, что такое конечное определение теоретически способно описывать бесконечно большое число объектов. С помощью рекурсивной программы возможно описать бесконечное вычисление, причём без явных повторений частей программы.
// генератор чисел Фибоначчи
#include
#include
int fib(int i) if (i
Слайд 17Лекция 23.09.13г.
Рекурсия в программировании
Классический пример рекурсии – вычисление факториала целого
числа:
// рекурсия (факториал)
#include
#include
int fact(int n) return (n>2)
? n * fact(n-1) : n;
>
main() int n;
for(n = 0; n
Слайд 18Лекция 23.09.13г.
Задача о Ханойской башне
Рисунок ниже иллюстрирует древнюю игру, известную
под названием Ханойской башни. Игра начинается, когда n дисков разного
диаметра расположены по возрастанию диаметров на одном из трех стержней. Цель игры — по одному перенести диски, чтобы они в конечном счете были расположены в том же порядке на другом стержне. Не разрешается класть диск большего диаметра на диск меньшего диаметра. Разработать алгоритм, который проделывает эту процедуру за 2n-1 операций, где под операцией подразумевается перемещение диска с одного стержня на другой.
Источник: theslide.ru
Функциональная структура программы
Работа представляет собой программу (реализованную на языке Microsoft Visual Basic 6), основной функцией которой является нахождение формулы производной на основании введенной пользователем исходной формулы, представляющей собой суперпозицию (произвольное сочетание) элементарных функций (предусмотрены программой sin, cos, tg, ctg, arcsin, arccos, arctg, arcctg, ln, exp, +, -, *, /, ^, константы).
Для удобства программа обладает дополнительными функциями: нахождение значения формулы при данных аргументах, приближенное нахождение интеграла, работа с переменными (изменение аргументов), вызов справки.
Программа использует стандартные библиотеки Microsoft Windows (98, XP, 2000), поэтому для корректной работы программы необходимо использовать эту операционную систему.
Техническое задание
Основное окно программы в рабочем режиме показано на рис 1.

o меню команд в верхней части экрана;
o поле для ввода формулы, включающее
o список переменных,
o поле для ввода строки;
o список задач, включающий:
o три кнопки «Производная», «Интеграл», «Значение»;
o два текстовых поля для ввода границ интегрирования;
o текстовое поле для вывода формулы;
o список допустимых функций (объект класса ListBox);
o таблица переменных, включающая:
o таблицу класса MSHFlexGrid библиотеки «MSHFLXGD.OCX»,
o три кнопки управления таблицей «Значение», «Новая переменная», «Сброс».
Выбор команды
· Для выбора команды используется одноуровневое горизонтальное меню.
· Для перемещения по меню используются клавиши навигации и / или мышь.
· Для выбора пункта используется клавиша Enter и / или левая клавиши мыши.
Команды меню
Файл -> Выход
При выходе программа заканчивает свою работу.
Действия -> Производная
Программа анализирует введенную формулу и в соответствующем поле выводит формулу производной. (При введении неверной формулы выводится ошибка).
Действия -> Интеграл
Программа анализирует введенную формулу и в соответствующем поле выводит значение частичных сумм под графиком функции. (При введении неверной формулы выводится ошибка).
Действия -> Значение
Программа анализирует введенную формулу и в соответствующем поле выводит значение функции при аргументах, указанных пользователем. (При введении неверной формулы выводится ошибка).
Справка -> Мне нужна помощь
На экране появляется окно, содержащее руководство пользователя.
Справка -> Об авторе
На экране появляется окно, содержащее информацию о создателе.
Поле для ввода формулы
Текст из этого поля используется в качестве исходной функции пользователя.
Список задач
Команды аналогичны командам меню.
Поле для вывода функции
Это поле служит для выведения конечного результата.
Список допустимых функций
Служит подсказкой пользователю как правильно написать функцию.
Двойной щелчок на элементе добавляет его в поле для ввода формулы.
Таблица переменных
Служит подсказкой пользователю, какие переменные можно использовать;
Двойной щелчок на элементе позволяет изменить значение переменной.
Таблица связана с тремя кнопками.
Значение переменной
Изменить значение выбранной переменной на указанной пользователем.
Новая переменная
Добавляет в таблицу новую переменную, имя которой указал пользователь.
Сброс переменных
Очищает таблицу переменных и создает переменные по умолчанию (x=0, y=0, z=0, t=0).
Введение
Алгоритм программы основан на теории математического анализа. В частности, в основу положены два утверждения:
– Все элементарные функции дифференцируемы на области определения. (Sin, cos, tg, ctg, arcsin, arccos, arctg, arcctg, ln, exp, +, -, *, /, ^, константы и т.д.)
– Суперпозиция дифференцируемых функций дифференцируема: (f (g(x)))’=g’ (x) f’ (g(x)).
Из этих утверждений следует, что любая суперпозиция элементарных функций дифференцируема.
В основу вычисления производной решено положить таблицу элементарных функций, т. к. любой суперпозиции элементарных функций соответствует список последовательных элементарных функций. Работа программы (т.е. выполнение необходимых процедур) сводится к составлению и анализу этой таблицы, а также проверки входных данных.
Например, при вводе функции y(x)=2^2+2sinx и нажатии кнопки «Производная» программа:
– вставляет символ «*» между 2 и sin x;
– берет x после sin в скобки;
– проверяет формулу на наличие синтаксических ошибок;
– составляет таблицу функции, которая выглядит следующим образом:
(https://megalektsii.ru/s25644t11.html» target=»_blank»]megalektsii.ru[/mask_link]