С каждой машиной Тьюринга связаны два конечных алфавита: алфавит входных символов А = 0, a1, …, am> и алфавит состояний Q = q0, q1 . qp > . (С разными машинами Тьюринга могут быть связаны разные алфавиты А и Q.) Состояние q0 называется заключительным, или состоянием останова. Считается, что если машина попала в это состояние, то она заканчивает свою работу. Состояние q1 называется начальным. Находясь в этом состоянии, машина начинает свою работу.
Входное слово размещается на ленте по одной букве в расположенных подряд ячейках. Слева и справа от входного слова находятся только пустые ячейки (в алфавит А всегда входит «пустая» буква а0 — признак того, что ячейка пуста).
Автомат может двигаться вдоль ленты влево или вправо, читать содержимое ячеек и записывать в ячейки буквы своего алфавита. Ниже схематично нарисована машина Тьюринга, автомат которой обозревает первую ячейку с данными.
Автомат каждый раз «видит» только одну ячейку. В зависимости от того, какую букву a1 он видит, а также в зависимости от своего состояния qt, автомат может выполнять следующие действия:
Машина Тьюринга. 2 часть. Решение задач.
- записать новую букву в обозреваемую ячейку;
- выполнить сдвиг по ленте на одну ячейку вправо/влево или остаться неподвижным;
- перейти в новое состояние.
Программа для машины Тьюринга представляет собой таблицу, в каждой клетке которой записана команда.
Клетка (qj, ai) определяется двумя параметрами — символом алфавита и состоянием машины.
Команда представляет собой указание: какой символ записать в текущую ячейку, куда передвинуть головку чтения/записи, в какое состояние перейти машине. Для обозначения направления движения автомата используем одну из трех букв: «Л» (влево), «П» (вправо) или «Н» (неподвижен).
После выполнения очередной команды МТ переходит в состояние q1 (которое может в частном случае совпадать с прежним состоянием qj). Следующую команду нужно искать в к-й строке таблицы на пересечении со столбцом, соответствующим букве, которую автомат видит после сдвига. В процессе работы автомат перескакивает из одной клетки программы, записанной в виде таблицы, в другую, пока не дойдет до клетки, в которой записано, что автомат должен перейти в состояние q0, т.е. остановиться. Будем говорить, что такие клетки содержат команду останова.
Если клеток останова в программе вообще нет или в процессе работы над входным словом МТ никогда не окажется в заключительном состоянии, то считается, что машина Тьюринга неприменима к данному входному слову. Машина Тьюринга применима к входному слову только в том случае, если, начав работу над этим входным словом, она окажется в заключительном состоянии.
Тьюрингом был описан универсальный исполнитель — машина Тьюринга, этот исполнитель способен решить любую алгоритмически разрешимую задачу. Почти одновременно с А.Тьюрингом (1937 г.) американский математик Эмиль Пост предложил иную абстрактную машину, характеризующуюся еще большей простотой, чем машина Тьюринга. Это строгое математическое построение было также предложено в качестве уточнения понятия алгоритма.
Матлогика 31. Машины Тьюринга
В машине Поста в ячейках бесконечной ленты можно записывать всего два знака: 0 и 1 (ставить метку в ячейку или стирать метку). Это ограничение не влияет на ее универсальность, так как любой алфавит может быть закодирован двумя знаками. Кроме ленты, в машине Поста имеется каретка (головка чтения/записи), которая:
- умеет двигаться вперед, назад и стоять на месте;
- умеет читать содержимое, стирать и записывать 0 или 1;
- управляется программой.
Как и машина Тьюринга, машина Поста может находиться в различных состояниях, но каждому состоянию соответствует не строка состояния с клетками, а некоторая команда одного из следующих шести типов (все строки в программе пронумерованы):
1. Записать 1 (метку), перейти к i-й строке программы;
- Записать 0 (стереть метку), перейти к i-й строке программы;
- Сдвиг влево, перейти к i-й строке программы i;
- Сдвиг вправо, перейти к i-й строке программы;
- Останов;
- Если 0, то перейти к i, иначе перейти к j.
Состояние машины — это состояние ленты и положение головки чтения/записи. Тезис Поста заключается в том, что: «Всякий алгоритм представим в форме машины Поста». Отсюда следует другое формальное определение алгоритма.
Алгоритм (по Посту) — программа для машины Поста, приводящая к решению поставленной задачи. Тезис Поста невозможно строго доказать, так же, как и тезис Тьюринга.
Источник: studfile.net
Правила выполнения программы машины Тьюринга
Во-первых, надо записать на ленту входное слово, к которому будет применена программа. Входное слово – это конечная последовательность символов, записанных в соседних клетках ленты; внутри входного слова пустых клеток быть не должно, а слева и справа от него должны быть только пустые клетки. Пустое входное слово означает, что все клетки ленты пусты.
Во-вторых, надо установить автомат в состояние q 1 (указанное в таблице первым) и поместить его под первым символом входного слова (рисунок 13.4).
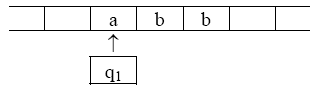
Рисунок 13.4 – Второй шаг выполнения программы
Если входное слово пустое, то автомат может смотреть в любую клетку, т.к. все они пусты.
После этих предварительных действий начинается выполнение программы. В таблице отыскивается ячейка на пересечении первой строки (т. к. автомат находится в состоянии q 1) и того столбца, который соответствует первому символу входного слова (это необязательно левый столбец таблицы), и выполняется такт, указанный в этой ячейке. В результате автомат окажется в новой конфигурации. Теперь такие же действия повторяются, но уже для новой конфигурации: в таблице отыскивается ячейка, соответствующая состоянию и символу этой конфигурации, и выполняется такт из этой ячейки. И так далее.
Когда завершается выполнение программы? Введём понятие такта останова. Это такт, который ничего не меняет: автомат записывает в видимую клетку тот же символ, что и был в ней раньше, не сдвигается и остается в прежнем состоянии, т. е. это такт S, N, q для конфигурации < S, q >. Попав на такт останова, МТ, по определению, останавливается, завершая свою работу.
В целом возможны два исхода работы МТ над входным словом:
1) первый исход – «хороший»: это когда в какой-то момент МТ останавливается (попадает на такт останова). В таком случае говорят, что МТ применима к задан ному входному слову. А то слово, которое к этому моменту получено на ленте, считается выходным словом, т.е. результатом работы МТ, ответом.
В момент останова должны быть выполнены следующие обязательные условия:
– внутри выходного слова не должно быть пустых клеток (отметим, что во время выполнения программы внутри обрабатываемого слова пустые клетки могут быть, но в конце их уже не должно остаться);
– автомат обязан остановиться под одним из символов выходного слова (под каким именно – не играет роли), а если слово пустое – под любой клеткой ленты.
2) Второй исход – «плохой»: это когда МТ зацикливается, никогда не
попадая на такт останова (например, автомат на каждом шаге сдвигается вправо и потому не может остановиться, т.к. лента бесконечна). В этом случае говорят, что МТ неприменима к заданному входному слову. Ни о каком результате при таком исходе не может идти и речи.
Отметим, что один и тот же алгоритм (программа МТ) может быть применимым к одним входным словам (т.е. останавливаться) и неприменимым к другим (т. е. зацикливаться). Таким образом, применимость/неприменимость зависит не только от самого алгоритма, но и от входного слова. На каких входных словах алгоритм должен останавливаться? На, так сказать, хороших словах, т.е. на тех, которые относятся к допустимым исходным данным решаемой задачи, для которых задача осмысленна. Но на ленте могут быть записаны любые входные слова, в том числе и те, для которых задача не имеет смысла; на таких словах поведение алгоритма не фиксируется, он может остановиться (при любом результате), а может и зациклиться.
Источник: studopedia.su
Если означенная клетка в программе машины тьюринга оказывается пустой то машина


Главное меню
Соглашение
Регистрация

Английский язык
Астрономия
Белорусский язык
Информатика
Итальянский язык
Краеведение
Литература
Математика
Немецкий язык
Обществознание
Окружающий мир
Русский язык
Технология
Физкультура
Для учителей
Дошкольникам
VIP — доступ
Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться

Получение сертификата
о прохождении теста
Источник: testedu.ru