Как решать 2 задание ЕГЭ по информатике и получить высший балл? Нужно заранее изучить таблицы истинности и законы алгебры логики. Решить эту задачу можно двумя способами – с помощью языков программирования Pascal или Pyton.
Важная информация
В этом обзоре мы поговорим о том, как делать 2 задание в ЕГЭ по информатике. Чтобы вы успешно справились с поставленной задачей, необходимо понимать, какие именно навыки будут проверяться.
От ученика требуется умение строить таблицы истинности и логические схемы. Решение 2 задания ЕГЭ по информатике (через Питон или иным способом) предполагает знание следующих областей предмета:
- Операции «импликация» и «эквивалентность»;
- Примеры законов алгебры логики;
- Эквивалентные преобразования логических выражений;
- Построение логического выражения с данной таблицей истинности;
- Логические функции;
- Логические уравнения;
- Дизъюнктивная нормальная форма.
И ещё несколько слов о том, как решать второе задание ЕГЭ по информатике. Чтобы успешно справиться с поставленной задачей, вам необходимо владеть умением анализировать алгоритмы с использованием таблиц. А также уметь строить математические объекты информатики, в том числе логические формулы. И уметь систематизировать знания, относящиеся к математическим объектам информатики.
Задание 2 | ЕГЭ по информатике | ДЕМО-2023
Для выполнения задания не требуется специализированное программное обеспечение, среднее время решения – 3 минуты. Максимальный балл за верный ответ – один.
Прежде чем смотреть на примерах, как решается это задание, вы должны запомнить важную информацию – обозначение функций вам еще пригодится.
| Логическая функция | Представление в Питоне или Паскале |
| ¬ или отрицание | not() |
| ∧ логическое умножение | and |
| ∨ логическое сложение | or |
| A ⟶ B следование | not(A) or B |
| ≡ или равносильность | = = |
На самом деле, это база, без которой не обойтись. Этих простых логических функций достаточно, чтобы суметь выстроить правильный алгоритм автоматического решения задачи. Что уже, давайте перейдём к практике, готовы?

На Паскале
Итак, во второй части нашего обзора вас ждёт подробный разбор, как решать 2 номер ЕГЭ по информатике. Давайте сначала посмотрим на условие задачи (это реальный пример из экзаменационной работы прошлых лет).
Миша заполнял таблицу истинности логической функции F
Но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
| F | |||
| 1 | 1 | 1 | |
| 1 | |||
| 1 | 1 |
Задание 2 | ЕГЭ по информатике | ДЕМО-2022
Определите, какому из столбцов таблицы соответствует каждая из переменных w, x, y, z.
Первым делом разберёмся, как строится решение 2 задачи ЕГЭ по информатике на Паскале.
Итак, открываем PascalABC.NET и вводим следующее значение:
Writeln (‘x, y, z, w‘);
for var x:=false to true do
for var y:=false to true do
for var z:=false to true do
for var w:=false to true do
if not (not y or (x=w)) and (not z or x) then
После этого запускаем и смотрим, что появится в окне вывода – становится понятнее, как решать вторую задачу ЕГЭ по информатике:
| x, | y, | z, | w, |
| False | True | False | True |
| True | True | False | False |
| True | True | True | False |
Напомним, что 0 – это False, а 1 – соответственно, True. Давайте сопоставим таблицы:
- В четвёртом столбце мы видим два нуля – нам подходит вариант w или z;
- В третьем столбце мы видим две единицы – подходят варианты x и y.
Соотносим другие данные и получаем такую последовательность букв в ответе: wxyz.
Вот вам подробный разбор 2 задания ЕГЭ по информатике. Как видите, с помощью языка программирования можно быстро найти правильный ответ – программа посчитает все за вас, вам нужно приложить лишь немного усилий.

На Питоне
Сейчас давайте поговорим о том, как быстро решать 2 задание ЕГЭ по информатике на Питоне. Это ещё один вариант, которым может воспользоваться ученик, который хочет сэкономить время на решении этой задачи.
В третьей часть обзора разберём несколько измененную задачу с другим ответом (также из демо-версии прошлых лет). Итак, начинаем решение 2 номера ЕГЭ по информатике через Питон.
Миша заполнял таблицу истинности функции
Но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцов таблицы соответствует каждая из переменных w, x, y, z.
| F | |||
| 1 | 1 | ||
| 1 | 1 | 1 | |
| 1 | 1 |
Определите, какому из столбцов таблицы соответствует каждая из переменных w, x, y, z.
Приступаем к решению второго задания ЕГЭ по информатике на Python. Делаем следующее:
for x in range(0, 2):
for y in range(0, 2):
for w in range(0, 2):
for z in range(0, 2):
if not( not(( x == (not(y)) )) or ((x and w) == z) ):
В результате мы получим следующую таблицу истинности:
| x | y | z | w |
| 1 | 1 | ||
| 1 | 1 | 1 | |
| 1 | 1 | ||
| 1 | 1 |
Заканчиваем разбор второго задания ЕГЭ по информатике соотнесением данных:
- Сначала вычеркиваем последнюю строку из таблицы истинности;
- Сразу видно, что второй столбец – переменная z;
- В третьем столбце x – на основании того, что у этой переменной есть два значения False и одно – True;
- В первом столбце ставим y, так как у нее есть две единицы;
- По остаточному принципу для последнего столбца остается переменная w.
Соответственно, ответ на это задание – yzxw.

Надеемся, вам стало понятнее, как выполнять 2 задание в ЕГЭ по информатике. В целом, если вы умеете пользоваться таблицами истинности и логическими схемами, всё будет хорошо – вы обязательно справитесь с этим вопросом и получите заслуженный бал.
Источник: udalenking.ru
ЕГЭ по информатике 2022 — Задание 2 (Ай да Питон!)

Продолжаем наш видеокурс по подготовке к ЕГЭ по информатике 2023. Сегодня разоблачим второе задание!
Кто незнаком с основными логическими операциями, можете посмотреть прошлогоднюю статью по заданию 2 из ЕГЭ по информатике.
В этой статье будут раскрыты методики решения 2 задания через язык программирования Питон.
Будем перебирать для каждой логической переменной все возможные варианты в программе. А логическая переменная всего два значения может принимать: 1 или 0 (истину или ложь). Таким образом, если к примеру у нас 4 переменные, мы получим 2 4 =16 различных комбинаций.
Кто знаком с мощнейшим методом для 2 задания из ЕГЭ по информатике, о котором я рассказывал в прошлогодней статье, тот поймёт, что мы будем применять тот же самый мощнейший метод, но автоматизированный с помощью питона.
Получить доступ к статьям из видеокурса
по подготовке к ЕГЭ по информатике 2023
Стоимость: 1200 499 рублей
Источник: code-enjoy.ru
Разбор 2 задания из ЕГЭ по информатике 2023

Логические выражения несколько отличаются от обычных математических. Например, Выражение 1 + 1 = 1 не имеет никакого смысла с точки зрения математики, но абсолютно верно с точки зрения логики. Логика оперирует понятиями Истина и Ложь, или True и False, или 1 и 0. Поэтому логическая сумма двух истинных высказываний также является истинной.
Цель урока: научиться строить таблицы истинности и логические схемы сложных логических выражений и решать задание №2 из ЕГЭ по информатике 2023.
Задачи урока:
- повторить определение логических операций;
- повторить таблицы истинности простых логических выражений,
- вспомнить порядок выполнения логических операций,
- записать законы алгебры логики,
- научиться упрощать сложные логические выражения,
- изучить понятия нормальной дизъюнктивной и нормальной конъюнктивной формы.
Кастинг на самого харизматичного преподавателя информатики!
Станьте звездой онлайн-вебинаров по ЕГЭ в Skysmart от Skyeng и получайте средний доход 200 000 ₽.

Повторяем определение логических операций
В алгебре логики изучаются логические операции, производимые над высказываниями. Такие высказывания могут быть истинными или ложными. Применяя к простым высказываниям логические операции, можно строить составные высказывания.
Повторим основные логические операции (буквами A, B или C будем обозначать элементарные логические высказывания):
Отрицание (инверсия, логическое НЕ) — это логическая операция, которая делает ложное высказывание истинным, а истинное — ложным.
Обозначение: ¬A, или not(A), или НЕ(A), или
Таблица истинности:
| A | |
| 1 | |
| 1 |
Логическое сложение (дизъюнкция, логическое ИЛИ) — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно, и ложно тогда и только тогда, когда оба простых логических выражения ложны.
Обозначение: A ∨ B, или A or B, или A ИЛИ B, или A + B
Таблица истинности:
| A | B | A+B |
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 | 1 |
Логическое умножение (конъюнкция, логическое И) — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложное выражение ложно.
Обозначение: A ∧ B, или A and B, или A И B, или A * B
Таблица истинности:
| A | B | A * B |
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
Логическое следование (импликация) — это сложное логическое выражение, которое истинно во всех случаях, кроме того случая, когда из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое (А) является условием, а второе (В) является следствием.
Обозначение: A → B
Таблица истинности:
| A | B | A → B |
| 1 | ||
| 1 | 1 | |
| 1 | ||
| 1 | 1 | 1 |
Логическая эквивалентность (равносильность) — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Обозначение: A ≡ B
Таблица истинности:
| A | B | A ≡ B |
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
Логическая операция XOR (сложение по модулю 2 или исключающее ИЛИ) — это логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …».
Обозначение: A ⊕ B
Таблица истинности:
| A | B | A ⊕ B |
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
Вспоминаем порядок выполнения логических операций
Порядок выполнения логических операций в сложном логическом выражении:
- Инверсия
- Конъюнкция
- Дизъюнкция
- Импликация
- Эквивалентность
Для изменения указанного порядка выполнения логических операций используются скобки.
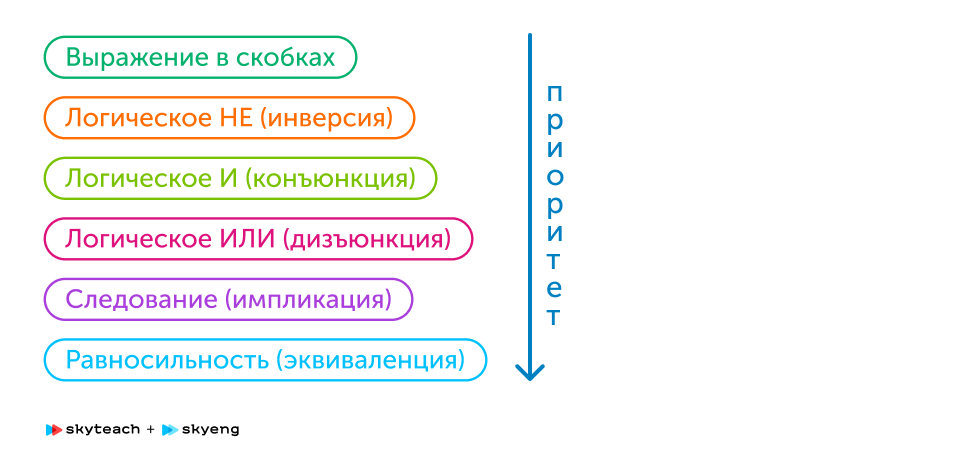
Законы алгебры логики — это некоторые стандартные преобразования логических выражений, при которых сохраняется равносильность.
1. Законы поглощения констант
2. Законы поглощения переменных
3. Законы идемпотентности
4. Закон двойного отрицания
= А
5. Закон противоречия
A * = 0
6. Закон исключенного третьего
A + = 1
7. Законы коммутативности
8. Законы ассоциативности
(A * B) * C = A * (B * C)
(A + B) + C = A + (B + C)
9. Законы дистрибутивности
A * (B + C) = (A * B) + (A * C)
A + (B * C) = (A + B) * (A + C) — обратите особое внимание!
10. Законы де Моргана
Правило для запоминания: «Крыша упала, знак поменяла (+ на *, * на +)».
11. Законы поглощения
12. Закон преобразования импликации
A → B = + B — импликация из A в B равна «не A плюс B»
Учимся упрощать сложные логические выражения
После этого можно тренироваться в упрощении логических выражений.
Логическое выражение будем обозначать буквой F. В качестве упрощения логического выражения удобно заменить логические символы конъюнкции и дизъюнкции на * и +, а затем можно избавиться и от импликации (при использовании программного метода импликацию в логическом выражении заменяют на выражение <=).
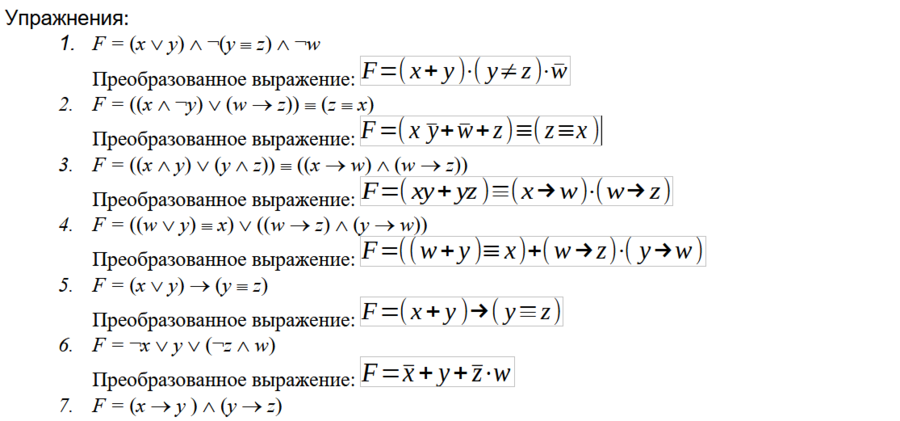
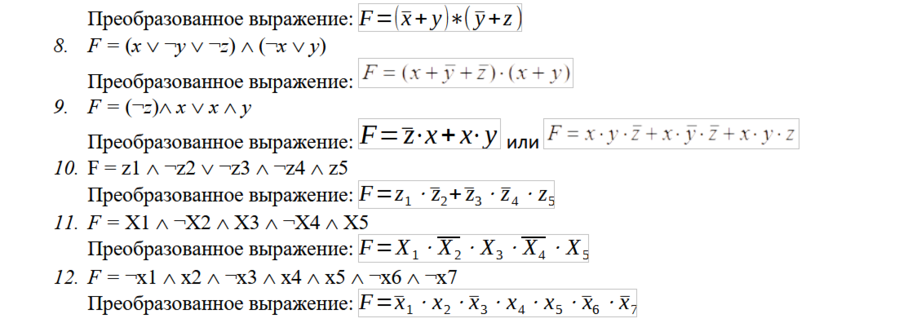
А как преподают компьютерные курсы в Skysmart? Какие есть направления для преподавания? Подробности по ссылке!

Практикуемся выполнять задание №2 ЕГЭ
Теперь можно переходить к изучению тонкостей и особенностей решения задания №2 по информатике.
На это задание по рекомендации ФИПИ требуется 3 минуты. Чтобы успешно справиться с ним, необходимо уметь строить таблицы истинности и логические схемы.
Строим таблицы истинности и логические схемы
Таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных. Если известна только часть таблицы истинности, соответствующее логическое выражение однозначно определить нельзя, поскольку частичной таблице могут соответствовать несколько разных логических выражений (не совпадающих для других вариантов входных данных).
Количество разных логических функций, удовлетворяющих неполной таблице истинности, равно , где k — число отсутствующих строк.
Например, полная таблица истинности выражения с тремя переменными содержит 2 3 = 8 строчек; если заданы только 6 из них, то можно найти 2 8−6 = 2 2 = 4 разные логические функции, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся).
Очень хорошей помощью в решении этого задания будет полная таблица истинности данного в условии логического выражения.
Полную таблицу истинности легче всего составить в табличном редакторе (Excel) или с использованием языка программирования (Python).
После получения полной таблицы истинности остается провести анализ на соответствие строк данной в условии части таблицы строкам составленной. При анализе строк особое внимание следует обратить на значение выражения в таблице истинности.
Если выражение равно 0, то нужно постараться привести данное в условие выражение к виду A + B + C + … . Логическая сумма A + B + C + … равна 0 (выражение ложно) тогда и только тогда, когда все слагаемые одновременно равны нулю, а в остальных случаях равна 1 (выражение истинно).
Если выражение равно 1, то приводите выражение к виду A · B · C · … . Логическое произведение A · B · C · … равно 1 (выражение истинно) тогда и только тогда, когда все сомножители одновременно равны единице, а в остальных случаях равно 0 (выражение ложно).
И еще два факта, которые пригодятся при анализе: логическое следование (импликация) А → В равно 0 тогда и только тогда, когда A (посылка) истинна, а B (следствие) ложно; эквивалентность А º B равна 1 тогда и только тогда, когда оба значения одновременно равны 0 или одновременно равны 1.
Используем 3 способа решения задания
Способы решения задания:
- ручной;
- с помощью электронных таблиц;
- с помощью языка программирования (Python).
Ручной способ решения
При ручном способе решения особенно важно сначала упростить выражение, данное в условии задачи, то есть привести логическое выражение к такому виду, который будет удобнее анализировать.
Например, если в условии представлена часть таблицы истинности, в которой значение выражения равно 1 — то можно постараться привести логическое выражение к нормальной дизъюнктивной форме (ДНФ — произведение нескольких литералов). Тогда выражение будет истинным, только если каждый литерал (сомножитель) будет истинен.
Если же в таблице истинности логическое выражение равно 0 — приводим выражение к нормальной конъюнктивной форме (КНФ — сумма нескольких литералов). В этом случае выражение будет ложным, только если каждый литерал (слагаемое) ложен.
После преобразования логического выражения производится анализ данной в условии таблицы истинности (или ее фрагмента) и для каждого столбца находится его значение (x, y и т. д.)
Решение с помощью электронных таблиц
При использовании электронных таблиц самым сложным является ввод в ячейку таблицы выражения, данного в условии в нотации, соответствующей программе. Чаще всего в качестве программ электронных таблиц используются электронные таблицы пакетов Libre Office, Open Office или Microsoft Office (Excel). Последняя — наиболее распространенная, поэтому здесь будем говорить про нее.
Шаг 1. Сначала количество столбцов в электронной таблице равно количеству переменных логического выражения. Каждый столбец обозначается по именам переменных логического выражения.
Шаг 2. Затем добавляется количество строк электронной таблицы, равное , где k — количество переменных логического уравнения.
Шаг 3. После этого создается еще один столбец электронной таблицы, в первой строке которого (не заголовка) записывается формула, соответствующая логическому выражению. Растянув эту формулу при помощи маркера автозаполнения на все строки таблицы, получаем полную таблицу истинности выражения.
Таблица функций электронной таблицы Excel и их соответствия логическим операциям:
| Логическая операция | Строка Excel |
| Инверсия | =ЕСЛИ(A2=1;0;1) |
| Дизъюнкция | =ЕСЛИ(ИЛИ(A2=1;B2=1);1;0) |
| Конъюнкция | =ЕСЛИ(И(A2=1;B2=1);1;0) |
| Импликация | =ЕСЛИ(И(A2=1;B2=0);0;1) |
| Эквивалентность | =ЕСЛИ(A2=B2;1;0) |
Решение с помощью языка программирования (Python)
При использовании программы на языке Python можно описать функцию, например так:
def f(arg):
x, y, z, w = arg
return (здесь записывается логическое выражение),
а затем, используя полный переборный алгоритм, перебрать значения 0 и 1 для каждой переменной во вложенных циклах и провести проверку истинности выражения:
print (‘x y w z’) # заголовок таблицы (в алфавитном порядке)
k = 0, 1 # k — кортеж констант (0 — False, 1 — True)
for x in k:
for y in k:
for w in k:
for z in k:
if f(x, y, w, z) == 1:
print(x, y, w, z) # если F = 1
Или просто вывести таблицу истинности print(x, y, w, z), не используя условный оператор во внутреннем цикле.
Полученную таблицу истинности остается проанализировать вручную и записать единственно верный ответ.
Для того чтобы записать логическое выражение на Python, воспользуйтесь следующей таблицей:
| Обозначение | Название | Оператор в Python |
| ∧ | конъюнкция | and |
В Python логическое значение True воспринимается как 1, а False — как 0, благодаря этому можно использовать обычное умножение *
| ∨ | дизъюнкция | or |
В Python логическое значение True воспринимается как 1, а False — как 0, благодаря этому можно использовать обычное сложение +
| ¬ | отрицание | not() |
| ≡ | тождество | == |
| ⊕ | строгая дизъюнкция | != |
| → | импликация | not(a) or b или not a or b или a |
Желаем вашим ученикам высоких баллов по ЕГЭ!
Источник: skyteach.ru