т.е. как отношение времени решения задач на скалярной ЭВМ к времени выполнения параллельного алгоритма (величина n применяется для параметризации вычислительной сложности решаемой задачи и может пониматься, например, как количество входных данных задачи).
Эффективность использования процессоров параллельным алгоритмом при решении задачи определяется соотношением: (величина эффективности определяет среднюю долю времени выполнения алгоритма, в течение которой процессоры реально задействованы для решения задачи).
Из приведенных соотношений можно показать, что в наилучшем случае и .
При практическом применении данных показателей для оценки эффективности параллельных вычислений следует учитывать два важных момента:
1. При определенных обстоятельствах ускорение может оказаться больше числа используемых процессоров — в этом случае говорят о существовании сверхлинейного ускорения. Несмотря на парадоксальность таких ситуаций (ускорение превышает число процессоров), на практике сверхлинейное ускорение может иметь место.
Лукьяненко Д.В. — Параллельные вычисления — 4.Эффективность и масштабируемость параллельных программ
Одной из причин такого явления может быть неодинаковость условий выполнения последовательной и параллельной программ. Например, при решении задачи на одном процессоре оказывается недостаточно оперативной памяти для хранения всех обрабатываемых данных и тогда становится необходимым использование более медленной внешней памяти (в случае же использования нескольких процессоров оперативной памяти может оказаться достаточно за счет разделения данных между процессорами).
Еще одной причиной сверхлинейного ускорения может быть нелинейный характер зависимости сложности решения задачи от объема обрабатываемых данных. Так, например, известный алгоритм пузырьковой сортировки характеризуется квадратичной зависимостью количества необходимых операций от числа упорядочиваемых данных. Как результат, при распределении сортируемого массива между процессорами может быть получено ускорение, превышающее число процессоров. Источником сверхлинейного ускорения может быть и различие вычислительных схем последовательного и параллельного методов.
2. При внимательном рассмотрении можно обратить внимание, что попытки повышения качества параллельных вычислений по одному из показателей (ускорению или эффективности) могут привести к ухудшению ситуации по другому показателю, ибо показатели качества параллельных вычислений являются часто противоречивыми. Так, например, повышение ускорения обычно может быть обеспечено за счет увеличения числа процессоров, что приводит, как правило, к падению эффективности. И наоборот, повышение эффективности достигается во многих случаях при уменьшении числа процессоров (в предельном случае идеальная эффективность легко обеспечивается при использовании одного процессора). Как результат, разработка методов параллельных вычислений часто предполагает выбор некоторого компромиссного варианта с учетом желаемых показателей ускорения и эффективности.
При выборе надлежащего параллельного способа решения задачи может оказаться полезной оценка стоимости вычислений, определяемой как произведение времени параллельного решения задачи и числа используемых процессоров:
Параллельное программирование. Лекция 16b. Эффективность параллельных программ
В связи с этим можно определить понятие стоимостно-оптимального параллельного алгоритма как метода, стоимость которого является пропорциональной времени выполнения наилучшего последовательного алгоритма.
Оценка качества параллельных вычислений предполагает знание наилучших (максимально достижимых) значений показателей ускорения и эффективности, однако получение идеальных величин для ускорения и для эффективности может быть обеспечено не для всех вычислительно трудоемких задач.
1. Закон Амдаля. Достижению максимального ускорения может препятствовать существование в выполняемых вычислениях последовательных расчетов, которые не могут быть распараллелены. Пусть f есть доля последовательных вычислений в применяемом алгоритме обработки данных, тогда в соответствии с законом Амдаля ускорение процесса вычислений при использовании p процессоров ограничивается величиной:
Закон Амдаля характеризует одну из самых серьезных проблем в области параллельного программирования (алгоритмов без определенной доли последовательных команд практически не существует). Однако часто доля последовательных действий характеризует не возможность параллельного решения задач, а последовательные свойства применяемых алгоритмов. Поэтому доля последовательных вычислений может быть существенно снижена при выборе более подходящих для распараллеливания методов.
Следует отметить также, что рассмотрение закона Амдаля происходит в предположении, что доля последовательных расчетов f является постоянной величиной и не зависит от параметра n, определяющего вычислительную сложность решаемой задачи. Однако для большого ряда задач доля f=f(n) является убывающей функцией от n, и в этом случае ускорение для фиксированного числа процессоров может быть увеличено за счет увеличения вычислительной сложности решаемой задачи. Данное замечание может быть сформулировано как утверждение, что ускорение Sp=Sp(n) является возрастающей функцией от параметра n (данное утверждение часто именуется эффект Амдаля).
2. Закон Густавсона – Барсиса. Оценим максимально достижимое ускорение исходя из имеющейся доли последовательных расчетов в выполняемых параллельных вычислениях:
где τ(n) и π(n) есть времена последовательной и параллельной частей выполняемых вычислений соответственно.
Закон Густавсона – Барсиса: Sp = g+(1–g)p = p+(1–p)g.
За счет увеличения числа входных данных величина g может быть пренебрежимо малой, обеспечивая получение идеального возможного ускорения Sp=p.
Источник: cyberpedia.su
Настройка и ускорение программ в OpenMP
При распараллеливании программ, написанных с использованием OpenMP, надо стремиться к максимально большей независимости параллельных потоков друг от друга. При этом следует избегать ситуаций, когда одни параллельные потоки используют данные из других. Если таких ситуаций нет, то говорят, что параллельные потоки независимы по данным.
Таким образом, при разработке параллельных программ с применением OpenMP важно, анализируя параллельные алгоритмы , находить в них зависимости по данным и стараться устранять их по мере возможности. Часто зависимости по данным между петлями циклов могут быть исключены с помощью модификации алгоритмов. Ниже представлен пример цикла с зависимостью по данным между петлями цикла .
DO I = 2 , 5 A (I) = C * A (I -1) ENDDO
Далее представлено элементарное распараллеливание этого цикла :
c$omp parallel sections c$omp section A (2) = C * A (1) c$omp section A (3) = C * C * A (1) c$omp section A (4) = C * C * C *A (1) c$omp section A (5) = C * C * C * C * A (1) c$omp end sections nowait
Рассмотрим еще один пример программы с циклом, петли которого содержат зависимости по данным. Исходный фрагмент этой программы приведен в примере 6.4.
В примере 6.5 представлен пример распараллеленной версии программы. При распараллеливании вычисления индексов массивов были устранены операторы вычисления индексов по рекуррентным формулам.
Еще один характерный пример фрагмента программы с зависимостью по данным приведен в примере 6.6.
Распараллеливание этого фрагмента можно осуществить путем применения директивы OpenMP reduction к циклу do .
i1 = 0 i2 = 0 do i =1, n i1 = i1 + 1 B(i1) = … i2 = i2 + i A(i2) = … enddo
6.4. Пример фрагмента программы с циклом, петли которого содержат зависимости по данным
c$omp parallel do do i =1, n B( i ) = … A((i**2 +i)/2) = … enddo
6.5. Пример фрагмента программы с зависимостью по данным
do i = 1, n xsum = xsum + a (i) xmu1 = xmu1 * a (i) xmax = max (xmax, a (i)) xmin = min (xmin, a (i)) enddo
6.6. Пример фрагмента программы с зависимостью по данным
Из сказанного выше следует, что для эффективного распараллеливания циклов нужно по возможности обеспечить независимость петель вложенных циклов. При этом надо иметь в виду, что циклы с условными выходами, пример которых показан во фрагменте программы (пример 6.7), не распараллеливаются.
При распараллеливании вложенных циклов надо стремиться к вынесению независимых по данным петель циклов на верхний уровень и проводить распараллеливание только на этом уровне. Пример такого цикла приведен во фрагменте программы (пример 6.8). Распараллеливание такого цикла возможно только на самом верхнем уровне, т. е. по индексу k .
do i = 1, n a (i) = b (i) + c (i) if (a(i) .GT. amax) then a(i) = amax goto 100 endif enddo 100 continue
6.7. Пример нераспараллеливаемого цикла с условным переходом
do k = 1, n do j = 1, n do i = 1, n a (i, j) = a (i, j) + b (i, k) * c (k, j) enddo enddo enddo
6.8.
Пример цикла с независимостью по данным, вынесенной на верхний уровень
Эффективность параллельных программ и масштабируемость
После создания работающей параллельной программы обычно возникает проблема оценки ее эффективности. Под эффективностью параллельной программы понимают оценку ускорения, которое удается получить при переходе от последовательной версии программы к параллельной. Понятно, что такая оценка будет зависеть от числа параллельных процессоров.
Под масштабируемостью параллельной программы понимают изменение этой оценки в зависимости от числа параллельных процессоров.
Впервые теоретическая оценка эффективности параллельных программ предложена в работе [6.9]. В настоящее время эта оценка известна как закон Амдала, согласно которому максимальное ускорение A на параллельной вычислительной системе, содержащей p процессоров, удовлетворяет следующему неравенству
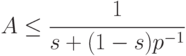
Здесь s — суммарная доля последовательных блоков в параллельной программе. Понятно, что 0
Из закона Амдала следует, что при числе параллельных процессоров, стремящемся к бесконечности, максимальное ускорение A не превысит величины 1/s вне зависимости от качества реализации параллельной части программы. При этом, если половина программы представляет из себя последовательную часть s=1/2 , то ускорить такую программу более чем в два раза не удастся при любом числе параллельных процессоров.
Еще одна интересная оценка, следующая из закона Амдала: для того чтобы ускорить программу на 8 параллельных процессорах, например в четыре раза, необходимо обеспечить, чтобы последовательная часть программы не превышала 1/7 части программы.
Таким образом, из закона Амдала видно, что при наличии в параллельных программах даже весьма незначительных последовательных частей происходит весьма существенное снижение быстродействия таких программ.
Источник: intuit.ru
1.2. Оценка эффективности параллельной программы
Само понятие эффективности параллельного алгоритма или программы всегда необходимо рассматривать в тесной связи с основной целью распараллеливания. Все задачи, решаемые на МВС, условно можно разделить на две группы:
- задачи, решение которых на однопроцессорных компьютерах в принципе возможно, однако требует больших временных затрат (осредненная оценка здесь примерно такова: задачу целесообразно распараллеливать, если время ее решения на современной однопроцессорной машине превышает 5-7 суток); к этой же группе следует отнести задачи, которые необходимо решать многократно на различных наборах исходных данных;
- задачи, для решения которых требуются вычислительные ресурсы, существенно превышающие возможности однопроцессорной техники (при этом во внимание принимается не только общий объем вычислений, но и необходимое количество оперативной и дисковой памяти).
Соответственно, с точки зрения конечного пользователя параллельная программа для решения задачи первой группы будет эффективна, если она позволит добиться существенного выигрыша по времени (в пять и более раз). В то же время при решении задач второй группы на первое место выходит оценка равномерности загрузки ресурсов многопроцессорной системы. Решение задач первой группы осуществляется, как правило, на МВС с небольшим количеством процессоров, и здесь все большее распространение получают вычислительные кластеры, собранные на основе традиционных одно- или двухпроцессорных персональных компьютеров. Для решения задач второй группы применяются мощные суперкомпьютеры, входящие в список самых высокопроизводительных вычислительных систем в мире Top-500 (http://www.top500.org), которые состоят из сотен и тысяч процессоров. В данном пособии мы будем ориентироваться на решение задач первой группы. Каким же образом можно оценить положительный эффект от перехода с последовательной программы к параллельной? Вернемся к примеру, рассмотренному в предыдущем параграфе. Проведем оценку общего времени вычислений для последовательной и параллельной программы. Пусть производительность одного процессора в рассматриваемых нами системах равна 
операций в секунду. Будем считать, что время, затрачиваемое процессором на выполнение операций сложения и умножения, одинаково. В последовательной программе выполняется 64 операции умножения и 32 операции сложения. Таким образом, общее время вычислений (без учета времени вывода результатов на экран) составит 
. Несложно убедиться, что для современных процессоров это время оказывается весьма и весьма малым. В самом деле, для приближенной оценки реальной (не пиковой!) производительности современных процессоров можно использовать величину, равную половине его тактовой частоты * ) . Так, если в нашем распоряжении имеется процессор класса Pentium 4 с тактовой частотой 3,2 ГГц, то его среднюю производительность можно оценить как 
GFlops (миллиардов операций с плавающей точкой в секунду). Подставляя данное значение производительности в приведенную выше формулу получим, что с решением нашей последовательной задачи указанный процессор справится за 6010 -9 с или 60 нс. Теперь оценим время, за которое выполнится наш параллельный алгоритм. В этом случае у нас имеется два типа операций: последовательные и параллельные. Параллельно у нас выполняются первая операция суммирования и две операции умножения (всего 96 операций, выполняющиеся параллельно на 32 процессорах), а последовательно (на нулевом процессоре) выполняются последние операции сложения (всего 31 операция). Таким образом, время работы параллельной программы будет складываться из времени работы ее параллельной и последовательной частей: 
раза быстрее, чем ее последовательный аналог. Отношение времени выполнения последовательной программы 
ко времени выполнения параллельной программы на
процессорах
называетсяускорением при использовании 
процессоров: 
. На практике эту величину вычислить можно не всегда, поскольку последовательной программы может просто не быть. Поэтому достаточно часто используется оценка ускорения вида 
, где 
– время выполнения параллельной программы на одном процессоре (в большинстве случаев оно превышает
в силу уже упоминавшегося повышения количества операций в параллельном алгоритме по сравнению с последовательным). Для рассматриваемого примера получим 
Видно, что оценка 
оказалась более оптимистичной (почти на треть), чем более аккуратная оценка
. Можно получить теоретическую оценку максимально возможного ускорения 
. Пусть
– общее количество операций в параллельной программе (предполагается, что
не зависит от числа процессоров
),
– доля этих операций, выполняемых последовательно,
– как и прежде, производительность отдельного процессора. Тогда справедливы оценки: 
. Данная оценка может оказаться весьма грубой, поскольку не учитывает время, затрачиваемое на передачу данных между процессорами. Таким образом, в общем случае имеем 
. Это соотношение носит название закона Амдаля. Из закона Амдаля следует, что для получения больших ускорений доля последовательных операций в параллельной программе должна быть весьма малой. Пусть мы хотим получить ускорение в 50 раз на 100-процессоорной системе. Тогда из закона Амдаля следует, что величина 
должна быть порядка 0,01, т.е. программа должна быть распараллелена на 99%! Добиться такого уровня распараллеливания в практических задачах бывает достаточно сложно. Другим важным параметром, с помощью которого оценивается качество параллельной программы, является эффективность использования процессоров: 
. Данный параметр показывает среднюю загруженность процессоров при работе параллельной программы. Для нашего примера имеем 
Таким образом, почти 90 % времени процессоры МВС будут простаивать. Следует отметить, что оценка 
(или
) является средней. В нашем примере нулевой процессор будет загружен на 100 %, поскольку он работает постоянно, в то время как время работы остальных процессоров составит порядка 8,8 % этого времени. 
Теперь обратимся к другому, возможно, самому важному вопросу, на который необходимо обращать внимание при написании параллельной программы – на организацию обмена данными. Во всех предыдущих оценках мы пренебрегали временем передачи данных. Тем не менее, оно может оказаться весьма значительным. Так, если мы запустим параллельную программу нашего примера, скажем, наAlpha-кластере УГАТУ, то мы не только не получим ожидаемого ускорения, но время работы параллельной программы окажется примерно в 30 000 раз больше, чем последовательного аналога! Причиной этого будут временные задержки при передаче данных. В общем случае время передачи данных зависит от многих факторов: пропускной способности сети передачи данных, параметров коммутирующего оборудования, принятой схемы маршрутизации, топологии вычислительной системы, количества и типа передаваемых данных, используемых для коммуникации функций и т.д. Так, уже упоминавшийся Alpha-кластер УГАТУ имеет топологию “звезда”, коммуникационную среду Fast Ethernet 100 Мбит/с и коммутатор со временем латентности 
равным (100-300)10 -6 с. В рассматриваемой нами простейшей параллельной программе у нас имеется 31 передача целочисленного значения от каждого ненулевого процессора нулевому. Соответственно, время собственно передачи данных (без учета времени подготовки сообщения и передачи служебной информации) составит 
нс. В приведенной формуле 
– размер передаваемого сообщения (количество элементов определенного типа),
– битовый размер типа,
– пропускная способность сети коммуникации. Между двумя последовательными передачами коммутатор дает случайную задержку, называемую временем латентности: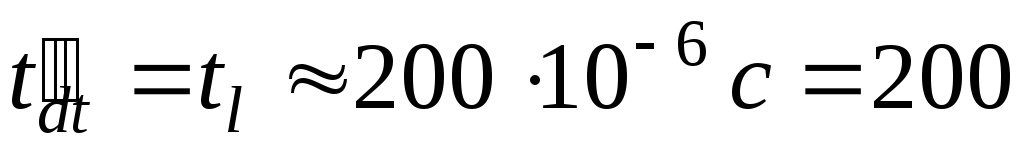 
мкс. Таким образом, общее время передачи можно оценить как сумму среднего времени латентности и времени собственно передачи данных: 
. Для нашего примера 
, поскольку
. Всего осуществляется
передача, поэтому суммарное время, затрачиваемое на коммуникации в параллельной программе, равно мкс = 
с. Общее время выполнения параллельной программы 
складывается из времени расчетов
и времени коммуникаций
: 
. Производительность процессора Alpha-кластера оценивается как 
GFlops, поэтому время выполнения последовательной программы будет оцениваться величиной 
с. Следовательно, в рассматриваемом примере время расчетов
, поэтому
. Обратим внимание на то, что время работы всей последовательной программы оказывается сопоставимо со временем передачи одного числа. Таким образом, для ускорения имеем 
, т.е. получаем уже упоминавшейся ранее результат. Как же можно повысить эффективность рассмотренной параллельной программы? Очевидно, что необходимо уменьшить количество передач данных, а для этого необходимо ввести новые способы коммуникации. Они будут подробно рассмотрены в последующих главах настоящего пособия, здесь же ограничимся замечанием, что в MPI существуют функции, позволяющие не только выполнять операции сборки данных на одном процессоре, но и сразу производить их суммирование. Разобранный пример позволяет сформулировать ряд требований, выполнение которых является необходимым для написания любой параллельной программы:
- объем вычислений, выполняемых на отдельном процессоре МВС, должен существенно превышать время, затрачиваемое на передачу данных с этого процессора; для программы в целом должно выполняться условие
;
- количество передач данных должно быть сведено к минимуму;
- доля последовательного кода в параллельной программе
должна быть как можно меньше; - объем вычислений на каждом процессоре должен быть примерно одинаковым, что обеспечит равномерную загрузку процессоров.
Источник: studfile.net