В декабре 1958 г. Верховный Совет СССР принял Закон об укреплении связи школы с жизнью и о дальнейшем развитии системы народного образования в СССР и в первом же номере журнала «Математика в школе» за 1959 г. в порядке обсуждения была опубликована статья «О перестройке программ по математике в свете новых задач школы». В ней, в частности, предлагалось внести ряд изменений в построение курса арифметики, прежде всего построить его таким образом, чтобы «основное внимание в нем уделялось не обыкновенным дробям, как это имеет место в настоящее время, а десятичным». [1] Авторы статьи утверждали, что навыки действий над десятичными дробями имеют большую практическую ценность, чем навыки действий над обыкновенными дробями (не считая самых простейших), что учащиеся владеют десятичными дробями значительно менее уверенно, чем обыкновенными и делали вывод: «Чтобы десятичным дробям могло быть уделено внимание на протяжении всего прохождения курса арифметики, целесообразно изучать их в V классе не после обыкновенных дробей, а перед ними». При этом предлагалось вводить десятичные дроби «не как частный случай обыкновенных, а в результате естественного продолжения принципа десятичной нумерации». Такой подход, по мнению авторов статьи, облегчал в известной мере изучение обыкновенных дробей и способствовал облегчению всего курса арифметики, «не снижая его общего научного уровня».
КАК НАУЧИТЬСЯ СЧИТАТЬ ДРОБИ / ВСЕГО 3 ПРАВИЛА
В следующем номере журнала Е.С.Березанская, Г.Б.Гуревич и А.П.Дицман указали на противоречивость аргументации, приведенной в статье, и дали подтвердившийся позднее прогноз: «Вопреки мнению авторов предлагаемая ими последовательность изучения курса арифметики приведет к снижению его научного уровня, так как сведется к заучиванию правил, а не к ясному представлению о сущности выполняемых операций».
Обсуждение проекта новой программы в Московском математическом обществе показало, что большинство выступавших положительно оценили усиление внимания авторов проекта к вычислениям с десятичными дробями, однако возражения против изменения традиционного порядка изучения дробей высказали К.П.Сикорский, Г.В.Давыдов, А.Г.Курош. Интересно высказывание П.С.Александрова по теме дискуссии: «…вести разговор о перенесении центра тяжести с простых дробей на десятичные, или обратно, это все равно, что при изучении таблицы умножения «перенести центр тяжести» на 2 и 5 и оставить на заднем плане умножение на 3 и 7, чтобы твердо знали, что 2х5 — это 10 и не совсем твердо, что 3х7 — это 21. Не может быть сомнений в том, что человек, окончивший среднюю школу, должен уметь складывать не только десятичные дроби, но и простые. И спорить об этом, по меньшей мере, несерьезно». [2]
Мудрый академик оказался неправ: спорить и серьезно отстаивать прежний порядок изучения дробей было необходимо. Тогда не отстояли — теперь восстанавливаем с большим трудом, когда прежние традиции почти утрачены, когда не только учителя, но и авторы учебников не придают значения нормальной логике развития материала в учебнике.
Как объяснить дроби? Что такое дробь? простое объяснение дробей. Как объяснить ребенку доли?
Заметим, что в России уже издавалась «Арифметика» В.Я.Буняковского (СПБ, 1852), в которой десятичные дроби были объединены с целыми числами в одном понятии «десятичных чисел», и действия с ними рассматривались до изучения действий над обыкновенными дробями. Специальная математическая комиссия при главном начальнике военно-учебных заведений, во главе которой в то время стоял М.В.Остроградский, поддержала такой порядок изучения дробей, считая, что это упростит изложение арифметики [3, с. 310]. Но предложенный порядок изучения дробей не закрепился в отечественной школьной практике.
В конце 50-х годов XX в. вместо анализа зарубежного опыта, причин, по которым этот подход не закрепился в практике отечественной школы, и поиска возможностей для совершенствования имевшихся тогда курсов арифметики была предпринята механическая перестановка разделов, которая привела не к упрощению, а к усложнению изложения материала, связанного с десятичными дробями. Чтобы в этом убедиться, давайте заглянем в первый же учебник арифметики под редакцией Н.Х.Спатару, появившийся на новой волне в 1960 г. [4]
Здесь после повторения действий с натуральными числами без всякого разговора об обыкновенных дробях вводятся десятичные дроби: «Число, которое содержит десятичные доли единицы, записанное по правилу записи натуральных чисел с помощью запятой, отделяющей целые единицы от десятых долей единицы, называется десятичной дробью». Дальше десятичные дроби сравнивают, складывают, вычитают и округляют. Изложение материала разворачивается достаточно неэкономно «от частного к общему». Изучается умножение десятичной дроби на 10, 100, 1000 и т.д., деление десятичной дроби на 10, 100, 1000 и т.д., умножение десятичной дроби на натуральное число (но не наоборот!), нахождение одной десятичной доли данного числа, нахождение десятичной дроби данного числа (чтобы найти десятичную дробь числа, нужно отбросить запятые, перемножить полученные натуральные числа и в произведении отделить справа запятой столько десятичных знаков, сколько их было вместе в данных числах). Заметьте, это все до нахождения, например, 2/3 числа.
Затем вводятся понятие процента и нахождение нескольких процентов числа. Только после этого дается умножение натурального числа на десятичную дробь (умножить на десятичную дробь, значит найти такую часть числа, которая выражена десятичной дробью) и умножение десятичной дроби на десятичную дробь (чтобы умножить одну десятичную дробь на другую, нужно опустить у дробей запятые, умножить полученные натуральные числа и в произведении отделить запятой столько цифр справа, сколько их было у множимого и множителя вместе [после запятой. — А. Ш.]). Наконец, определяется деление десятичной дроби на натуральное число и на десятичную дробь.
Позднее, при подготовке нового учебника Н.Я.Виленкина и др. описанную систему изложения материала упростили, введя ограниченный объем сведений об обыкновенных дробях перед изучением десятичных дробей. Этот порядок изучения дробей сохранился в учебнике до наших дней.
Дроби в каком классе изучают
Одну из сложных и важных тем раскрывает программа математики для пятиклассников – это дроби. Новизна этого раздела и его практическое значение вызывают большой интерес у детей при изучении.
Эта объемная тема вмещает в себе такие разделы: обыкновенные дроби, вычитание и сложение дробей с идентичными знаменателями, десятичные и неправильные дроби, а также арифметические операции с ними (вычитание, сложение, деление, умножение), сложение дробей с целыми числами и разными знаменателями.
Еще до изучения всех видов дробных чисел у ребенка имеется уже некоторый опыт в наблюдении частей целых объектов. На практике он сталкивался с необходимостью разделить целый объект на равные частички, например, расчертить школьную доску, отрезать четверть веревки, разрезать булочку, апельсин на четыре ровные части, разделить пополам шоколадку.
При прохождении данной темы, школьники встречаются со многими новыми возможностями и особенностями такого вида чисел, которые отличают дробные числа от натуральных: возможность, запись, название.
Виды дробей
Простое или обыкновенное дробное число – представлено в виде рациональных чисел, которые записаны как соотношение одного числа к другому. Делимое — принято считать числителем, делитель – знаменателем. Если знаменатель будет больше числителя, то это будет правильной дробью. Если же, знаменатель будет меньше или же равен числителю – это есть неправильная дробь.
Записывать неправильную дробь следует, как сложение правильной дроби и числа натурального ряда. Запись правильной дроби с обыкновенным числом – это есть смешанная дробь, подразумевает сумму этих чисел.
Десятичная дробь представлена дробным числом со знаменателем, где степень — число натуральное. Главной особенностью дроби есть то, что можно умножить (разделить) числитель и так же знаменатель на одно и то же число, которое не есть нулем. Эта особенность позволяет сводить дробные числа к общему знаменателю, что необходимо для выполнения арифметических действий (сравнение, сложение, вычитание).
Изучение всех видов дробей расширяет математическое представление о числах. Дети узнают, что, есть не только обыкновенные числа, а и дробные. Во время изучения дробей учитель показывает то общее, что присуще всем числам, и особенное, присуще только дробям. Все это формирует логическое мышление, умение видеть причинные связи, а так же внимание и наблюдательность.
О нас
Сайт был создан для старейшего журнала «Сельская новь». На данный момент мы сохранили анонсы номеров Сельской нови, но начинаем развивать тему фермерства в России
Читать далее.
Контакты
Наш адрес: 117105, г. Москва, Варшавское шоссе, д. 17, стр. 5
Телефон: 8 (495) 958 66 66
Облако тегов
Источник: www.novsel.ru
Как объяснить дроби ребенку?

Тема дробей — одна из самых непростых для школьников. Понять их неподготовленному ребенку, а тем более выполнять с ними операции, может быть достаточно сложно. Но даже самая трудная задача может стать простой и понятной, если правильно к ней подойти. Для детей нужно использовать фантазию, наглядность и элементы игры. А также – сохранять спокойствие и терпеливо объяснять, даже если это потребуется сделать много раз.
Как объяснить суть дробей ребенку?
Слово «дробь» будто говорит само за себя — оно означает дробление, деление. В школьной программе к изучению дробей приступают только в 5 классе, освоив все действия с целыми числами. Но знакомство с ними целесообразно начинать заранее, еще в старшем дошкольном возрасте. Это формирует пространственные представления у детей и тренирует логическое мышление.
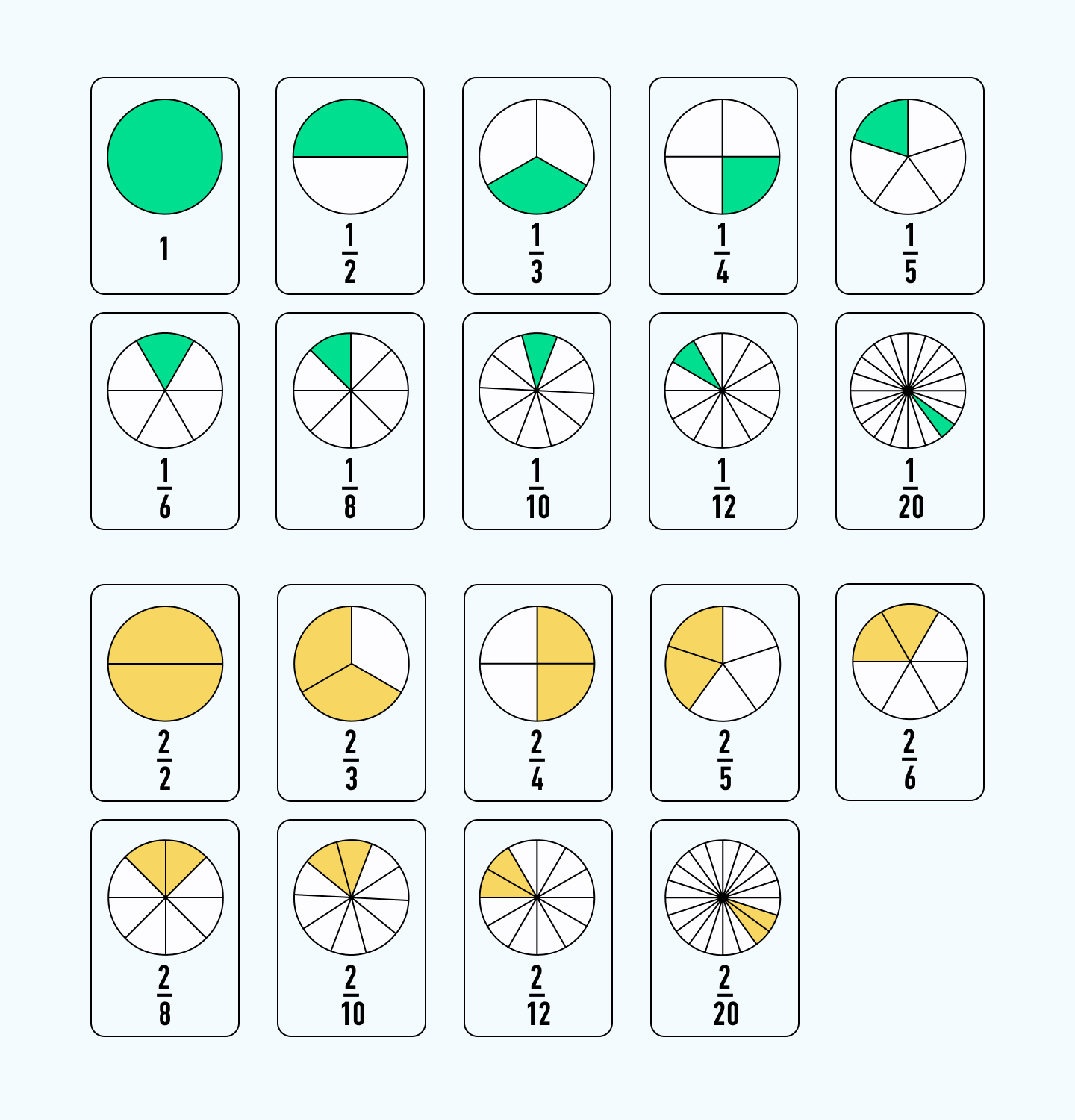
Для начала нужно объяснить ребенку понятие долей. Это очень легко сделать на наглядных повседневных примерах. Самый простой и доступный — еда. Например, пирог — целый. Разделить его можно на несколько одинаковых частей. Один кусочек такого пирога и будет называться одной долей из всех возможных.
Поделив пирог на четыре части, один кусочек называют одной четвертой частью.
Таким образом делить можно все, что угодно: яблоки, апельсины, плитки шоколада, конфеты в коробке и т. д. Еще один прекрасный наглядный материал для изучения дробей — кубики конструктора Lego. С их помощью можно поделить целое на равные части очень легко. Дети быстро запоминают форму кубиков, и им не требуется постоянно пересчитывать количество выступающих элементов на них.
Если ребенок увидит практическое применение дробей и востребованность их в реальной жизни, ему будет проще понять их и осознать важность получения математических знаний и навыков.
Что нужно знать о дробях?
1. Дробь — число нецелое, оно обозначает количество долей целого.
2. Дробь меньше целого.
3. Чем на большее число долей поделено целое, тем эти доли меньше и наоборот — чем долей меньше, тем они, соответственно, больше.
Для обозначения долей в математике используют понятие обыкновенная дробь. С ее помощью можно записать абсолютно любое необходимое количество долей.
Обыкновенная дробь представляет собой две части, именуемые числителем и знаменателем. Записываются они разделенными горизонтальной чертой либо наклонной вправо линией. Знаменатель пишется внизу либо справа от дробной черты, он показывает общее количество частей от целого, на которое оно было поделено. А числитель пишется вверху или слева от дробной черты и показывает, сколько долей целого сейчас взяли.
Вернемся к нашему пирогу. Очевидно, что разделить его реально на сколько угодно равных частей. В зависимости от того, на сколько частей его разделили, меняется и знаменатель дроби. У пирога, разделенного одной прямой линией на две части, знаменатель будет равен 2, у разделенного на три части — 3 и т. д. Числитель же, в свою очередь, показывает, сколько частей сейчас взято. Если взяли только одну часть из двух, то получится дробь 1/2, только две из трех — 2/3 и т. д.
Что такое смешанные дроби?
В математике выделяют дроби правильные и неправильные. Правильные — те, у которых числитель меньше знаменателя. Например: 1/3, 2/5, 4/12. Но бывает и так, что числитель становится больше знаменателя. Если объяснять предметно, то взято больше частей пирога, чем было тех, на которые он поделен.
Такое вполне возможно и в жизни, и в математике.
У таких дробей можно отделить целую часть и оставшуюся после этого дробную. То есть будет видно, сколько взято целых пирогов и плюс определенное количество его частей. Нужно хорошо представить себе описанное, или даже проверить на практике, а не просто заучивать формулы. Тогда сокращение дробей будет выполняться ребенком осмысленно и безошибочно.
Для того чтобы трансформировать неправильную дробь в смешанное число, следует сперва числитель поделить на знаменатель. В результате почти всегда получим целое число и какой-то остаток. Целое число и нужно записать, как целую часть. А остаток — отправить в числитель дробной части. Неизменным остается только знаменатель.
Неправильными называют и дроби с одинаковым числом над и под дробной чертой: 6/6, 12/12 и т. д. Очевидно, что превратить их можно в 1. Наглядно это взято столько кусочков пирога, на сколько он и был поделен, т. е. целый пирог.
Примеры:
- 14/5 = (5*2+4) / 5 = 2 4/5
- 21/6 = (6*3+ 3) / 6 = 3 3/6
Задание:
Выделите целую часть из неправильных дробей:
Можно провести противоположную процедуру — превратить смешанное число в неправильную дробь. Эта операция часто применяется в математических вычислениях, поэтому будет полезным узнать о ней. Для этого нужно сперва умножить целую часть и знаменатель. Затем получившееся число прибавить к числителю, а знаменатель оставить прежним.
Примеры:
- 3 1/8 = (3*8+1) / 8 = 25/8
- 7 4/9 = (7*9+4) / 9 = 67/9
Задание:
1. Преобразовать в смешанное число неправильную дробь:
2. Выполнить обратную первой задачу — смешанное число превратить в неправильную дробь:
Десятичные дроби
Дроби, в знаменателях которых есть числа, кратные десяти — 10, 100, 1000 и т. д. — в математике можно обозначать следующим образом. Сначала пишется целая часть, а потом числитель из дробной части, отделенный запятой.
Например, 5 4/10 попробуем записать в виде десятичной дроби. Пишем целую часть (5), ставим запятую и далее пишем числитель дробной части (4). Получаем: 5,4. Читается эта дробь так: «пять целых и четыре десятых». Число, представленное в таком виде, именуется десятичной дробью.
Существуют также десятичные дроби без целой части. Например: 7/100. Как быть в таком случае? Чтобы записать подобную дробь, пишут ноль, ставят запятую и далее записывают числитель дроби — 0,07. Такая дробь читается как «ноль целых, семь сотых».
Десятичные дроби очень удобны, они используются в точных вычислениях. Десятичная система исчисления применяется человечеством с самых древних времен. Она интуитивна понятна и проста.
Задание:
Преобразовать следующие дроби в десятичные:
Сокращение дробей
Сокращение дробей выполняют для того, чтобы их упростить. Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей. Чтобы разобраться с этим, рассмотрим пару таких примеров.
Пример 1. Сократить дробь 8/12
Решение будет следующим. Наибольшее число, на которое делятся и 8, и 12, — это 4. Поэтому, чтобы сократить дробь, просто поделим ее числитель и знаменатель на 4:
8/12 = 8:4 / 12:4 = 2/3
Пример 2. Сократить дробь 10/25
Решение. Наибольшее число, на которое делятся и 10, и 25, — это 5. Потому, чтобы сократить дробь, поделим ее числитель и знаменатель на 5:
10/25 = 10:5 / 25:5 = 2/5
Несократимой называется дробь, у которой числитель и знаменатель имеют только один общий делитель — единицу.
Задание:
Сократите следующие дроби:
Сложение дробей
Сначала разберем сложение дробей с одинаковыми знаменателями. В этом случае операция предельно простая. Складываются числители дробей, а знаменатель остается прежним.
Примеры:
- 1/7 + 2/7 = 3/7
- 3/8 + 5/8 = 8/8 = 1
Задание:
Выполни сложение дробей с одинаковыми знаменателями:
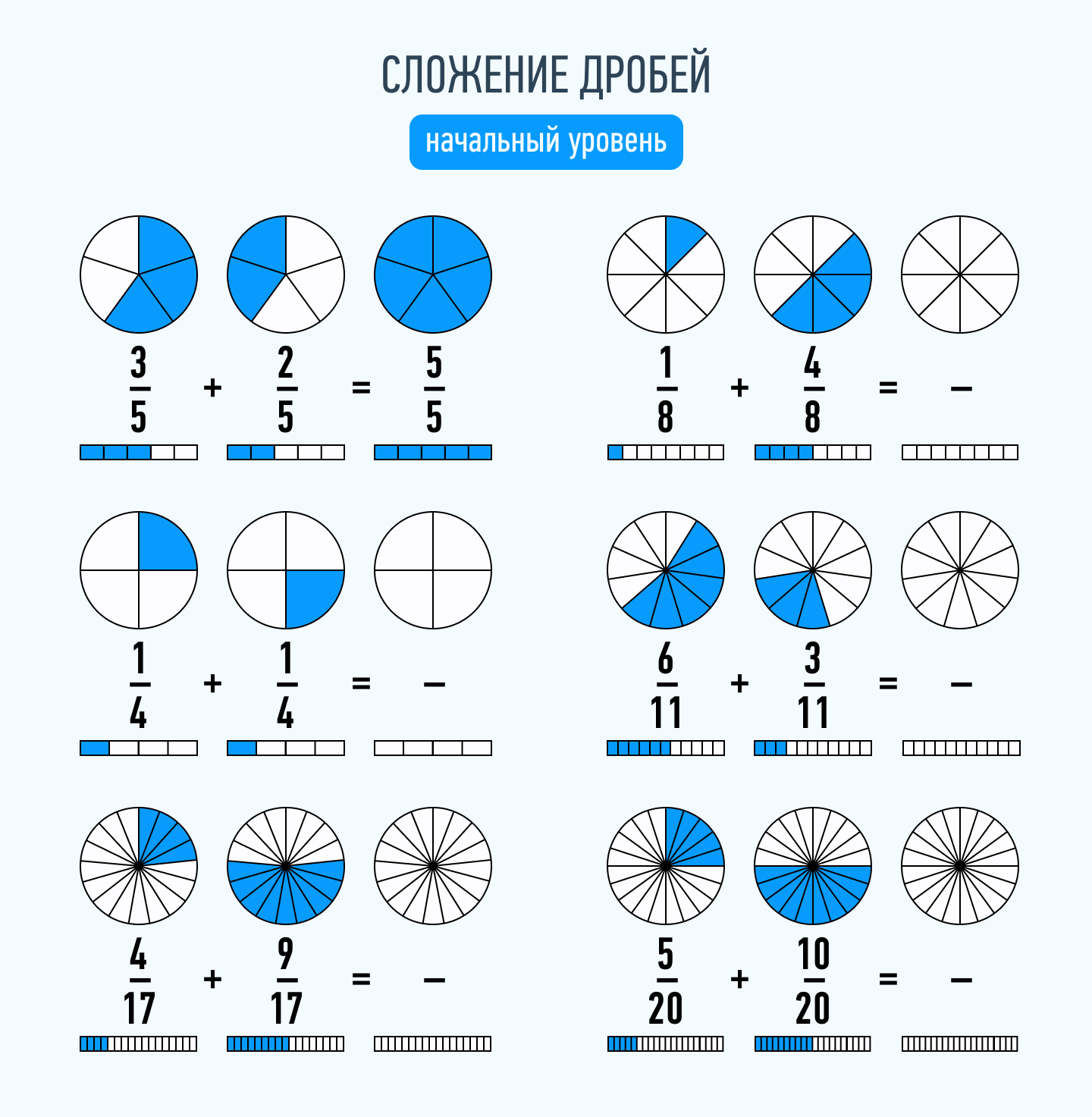
Но все усложняется, если нужно сложить дроби с разными знаменателями. В этом случае необходимо привести дроби к наименьшему общему знаменателю. Чтобы это сделать, необходимо найти наименьшее общее кратное. Это такое число, которое делится на оба эти числа без остатка. Например: 3/7 + 2/6.
Наименьшее общее кратное для чисел 7 и 6 будет 42.
Далее ищем дополнительные множители для каждой из дробей. Для этого найденное на предыдущем этапе наименьшее общее кратное делим по очереди на знаменатель каждой из дробей:
- 42 / 7 = 6 — это будет дополнительный множитель для 3/7;
- 42 / 6 = 7 — это, соответственно, дополнительный множитель для 2/6.
Обе части каждой из наших дробей, и числитель и знаменатель, умножаем на свой, определенный выше, множитель:
- 3*6 / 7*6 = 18/42;
- 2*7 / 6*7 = 14/42.
Складываем полученные дроби аналогичным образом, как уже разобранные выше дроби с одинаковыми знаменателями:
- 18/42 + 14/42 = 32/42
Если это возможно, то дробь сокращают. Если дробь получилась неправильная, то следует целую часть из нее выделить.
Задание:
Выполни сложение дробей с разными знаменателями:
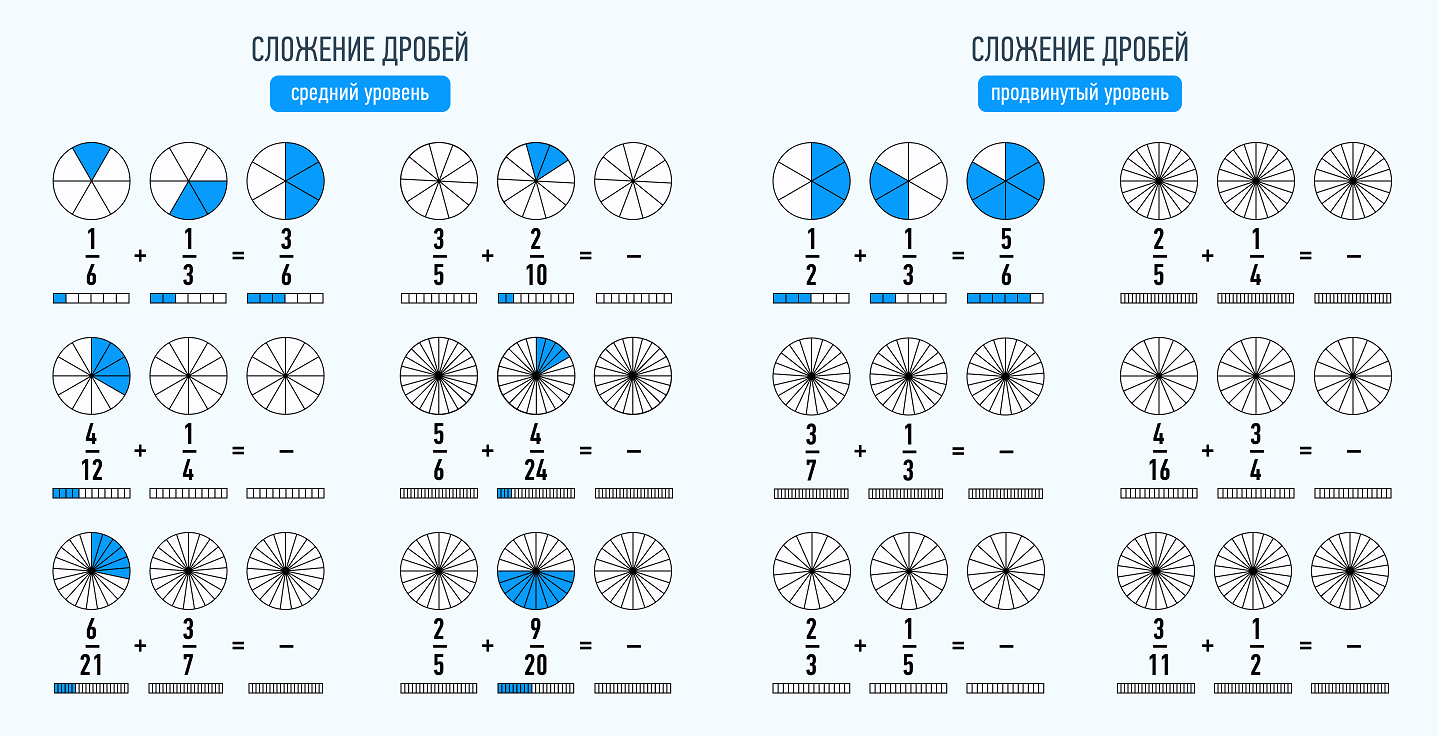
Вычитание дробей
Эта операция проводится аналогично сложению. Чтобы вычесть две дроби с одинаковыми знаменателями, нужно найти разность их числителей, а знаменатель оставить тем же.
Пример:
7/9 — 2/9 = (7-2) / 9 = 5/9
Задание:
Выполни вычитание дробей с одинаковыми знаменателями:
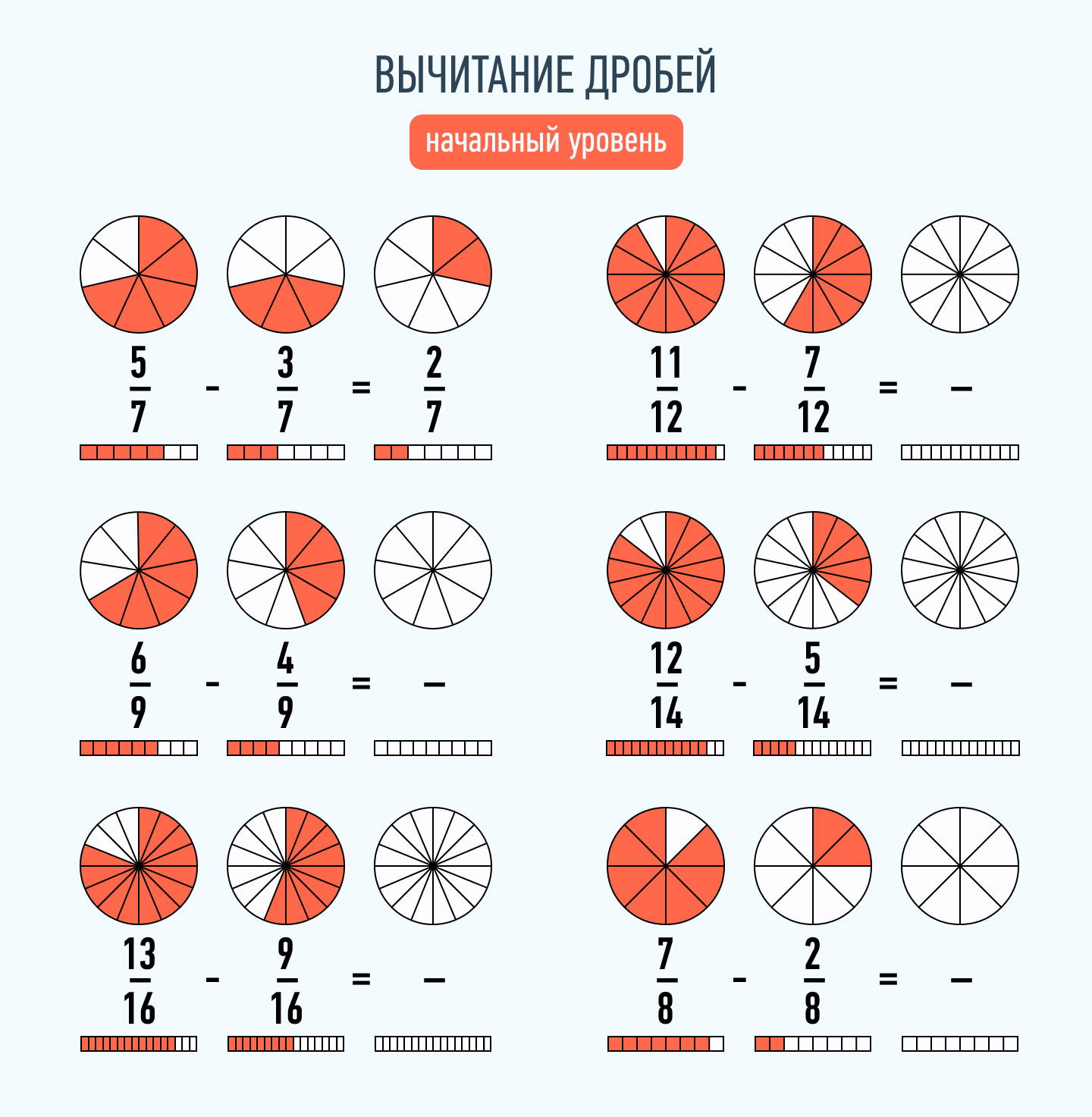
Для дробей с разными знаменателями также придется найти наименьшее общее кратное и дополнительные множители. Затем, по аналогии со сложением, произвести вычитание.
Пример:
6/7 — 8/10 = (6*10-8*7) / 70 = (60-56) / 70 = 4/70
Задание:
Выполни вычитание дробей с разными знаменателями:
Умножение дробей
Существует два варианта умножения дробей. Рассмотрим каждый из них в деталях.
Умножение обыкновенных дробей
В этом случае числители обеих дробей перемножаются — это будет новый числитель. Знаменатели обеих дробей также перемножаются — это будет новый знаменатель.
Пример:
2/5 * 3/4 = (2*3) / (5*4) = 6/20 = 3/10
Если это возможно, то следует сократить дроби перед перемножением. Это облегчит дальнейшие действия.
Пример:
24/35 * 25/36 = (24*25) / (35*36) = (2*5) / (7*3) = 10/21
Умножение смешанных дробей
Чтобы это сделать, необходимо превратить дроби в неправильные и далее действовать по алгоритму, приведенному в первом пункте.
Пример:
4 2/7 * 5 3/5 = 30/7 * 28/5 = (30*28) / (7*5) = (6*4) / (1*1) = 24/1 = 24
Задание:
Выполните умножение дробей:
- 5/7 * 6/8;
- 6/11 * 2/3;
- 2 3/7 * 4 5/9;
- 4 6/7 * 7 9/10.
Деление дробей
Освоив умножение, с делением также можно справиться легко. Правило деления дробей заключается в следующем: при делении одной дроби на другую нужно первую перемножить на обратную (перевернутую) вторую дробь. Или, иными словами, числитель первой умножить на знаменатель второй (это будет новый числитель), а знаменатель первой умножить на числитель второй (это будет новый знаменатель).
Пример:
4/7 : 2/5 = 4/7 * 5/2 = 20/14 = 10/7 = 1 3/7
Бывают ситуации, когда дробь нужно разделить на целое число. В этом случае следует представить дробь как неправильную. Числителем у нее будет это целое число, а знаменателем просто единица. Далее действовать нужно по уже знакомому правилу деления дробей из предыдущего случая.
Пример:
5/9 : 2 = 5/9 : 2/1 = (5*1) / (9*2) = 5/18
Задание:
Выполните деление дробей:
- 6/11 : 3;
- 7/15 : 2;
- 9/12 : 4.
Сравнение дробей
Если сравниваются дроби с одинаковыми знаменателями, то очевидно, что большей будет та, числитель у которой больше.
Пример:
Если сравниваются дроби с одинаковыми числителями, то большей будет та, знаменатель у которой меньше.
Пример:
1/2 > 1/8, так как числители одинаковы, а в знаменателе 8 больше 2.
Дроби же с разными знаменателями так просто не сравнишь. Нужно сперва определить их общий знаменатель и привести к нему обе дроби. Правила этой операции были приведены выше. Получим дроби, сравнить которые можно очень легко.
Пример:
Сравниваем дроби 2/5 и 1/10. Для этого приводим их к общему знаменателю — 10. Получаем 4/10 и 1/10. Теперь сравниваем дроби, уже имеющие одинаковые знаменатели: 4/10 > 1/10.
Есть один секрет, который нужно запомнить. Если одна из сравниваемых дробей неправильная, то она всегда больше правильной. Если подумать и вспомнить свойства дробей, то все становится понятно. Ведь неправильная дробь всегда будет больше единицы, тогда как правильная, наоборот, всегда будет меньше.
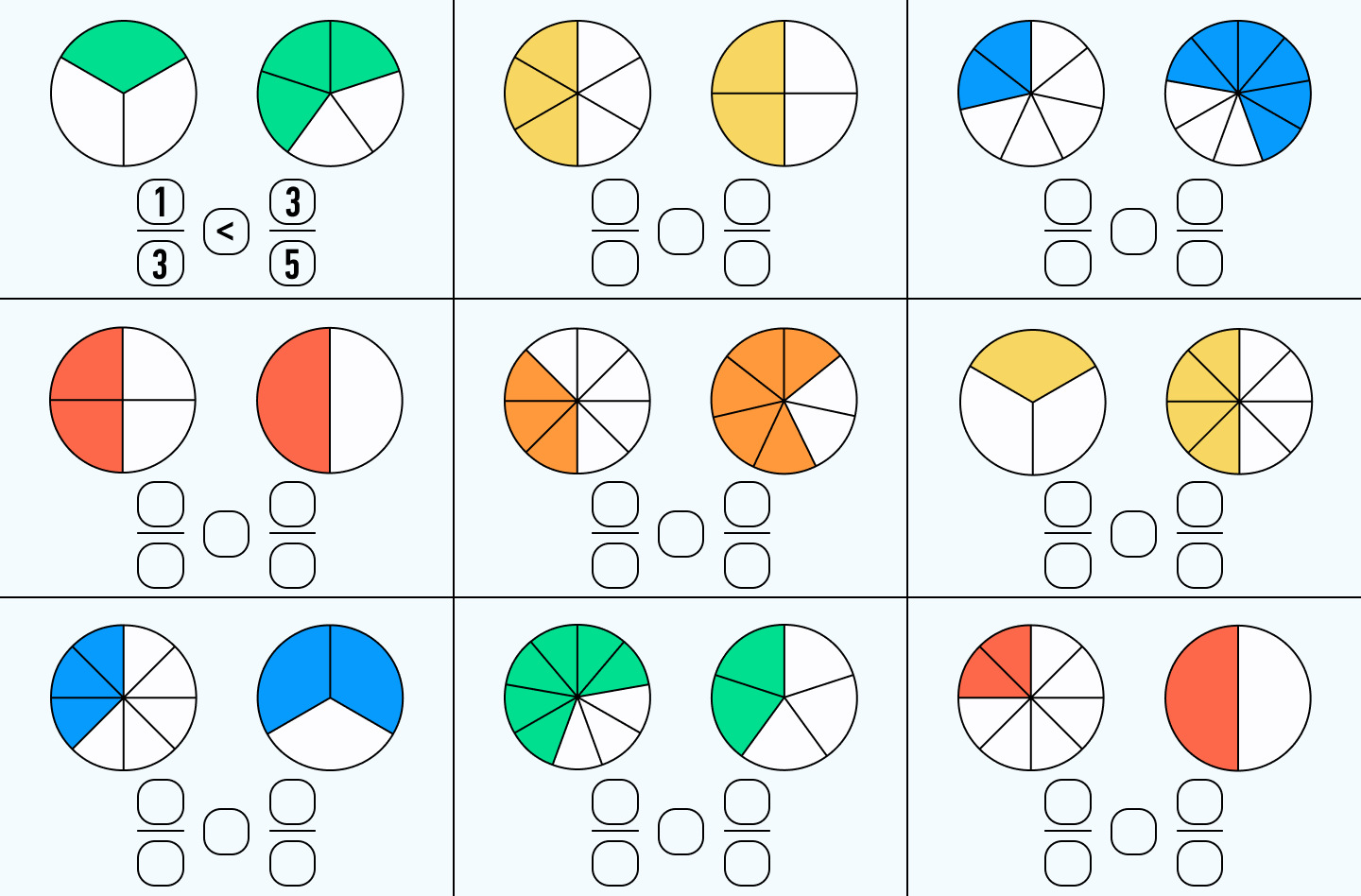
Задание:
Определите, какие дроби изображены на рисунке, и сравните их:
Итак, мы рассмотрели дроби, правила всех действий с ними. Надеемся, что наши объяснения и рекомендации будут очень полезны. Начинайте знакомить детей с дробями еще до школы. Хорошо усвоив эти понятия, ребенок без труда справится затем и с записью дробей, и с действиями с ними.


Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
- Таблица умножения для детей
- Как объяснить ребенку состав числа?
Источник: umnazia.ru