Как известно, универсальные вычислительные машины могут быть запрограммированы для решения самых разнородных задач — в этом заключается одна из основных их особенностей, имеющая огромную практическую ценность. Один и тот же компьютер, в зависимости от того, какая программа находится у него в памяти, способен осуществлять арифметические вычисления, доказывать теоремы и редактировать тексты, управлять ходом эксперимента и создавать проект автомобиля будущего, играть в шахматы и обучать иностранному языку.
Однако успешное решение всех этих и многих других задач возможно лишь при том условии, что компьютерные программы не содержат ошибок, которые способны привести к неверным результатам. Можно сказать, что требование отсутствия ошибок в программном обеспечении совершенно естественно и не нуждается в обосновании. Но как убедиться в том, что ошибки, в самом деле, отсутствуют?
Вопрос не так прост, как может показаться на первый взгляд. К неформальным методам доказательства правильности программ относят отладку и тестирование, которые являются необходимой составляющей на всех этапах процесса программирования, хотя и не решают полностью проблемы правильности.
Оценка сложности алгоритмов | О большое | Алгоритмы и структуры данных
Существенные ошибки легко найти, если использовать соответствующие приемы отладки (контрольные распечатки, трассировки). Тестирование – процесс выполнения программы с намерением найти ошибку, а не подтвердить правильность программы. Суть его сводится к следующему.
Подлежащую проверке программу неоднократно запускают с теми входными данными, относительно которых результат известен заранее. Затем сравнивают полученный машиной результат с ожидаемым.
Если во всех случаях тестирования налицо совпадение этих результатов, появляется некоторая уверенность в том, что и последующие вычисления не приведут к ошибочному итогу, т.е. что исходная программа работает правильно. Мы уже обсуждали понятие правильности программы с точки зрения отсутствия в ней ошибок.
С интуитивной точки зрения программа будет правильной, если в результате ее выполнения будет достигнут результат, с целью получения которого и была написана программа. Сам по себе факт безаварийного завершения программы еще ни о чем не говорит: вполне возможно, что программа в действительности делает совсем не то, что было задумано.
Ошибки такого рода могут возникать по различным причинам. В дальнейшем мы будем предполагать, что обсуждаемые программы не содержат синтаксических ошибок, поэтому при обосновании их правильности внимание будет обращаться только на содержательную сторону дела, связанную с вопросом о том, достигается ли при помощи данной программы данная конкретная цель.
Целью можно считать поиск решения поставленной задачи, а программу рассматривать как способ ее решения. Программа будет правильной, если она решит сформулированную задачу. Метод установления правильности программ при помощи строгих средств известен как верификация программ.
В отличие от тестирования программ, где анализируются свойства отдельных процессов выполнения программы, верификация имеет дело со свойствами программ. В основе метода верификации лежит предположение о том, что существует программная документация, соответствие которой требуется доказать.
Доказательство корректности ациклических программ
Документация должна содержать: спецификацию ввода-вывода (описание данных, не зависящих от процесса обработки); свойства отношений между элементами векторов состояний в выбранных точках программы; спецификации и свойства структурных подкомпонентов программы; спецификацию структур данных, зависящих от процесса обработки. К такому методу доказательства правильности программ относится метод индуктивных высказываний, независимо сформулированный К. Флойдом и П. Науром.
Суть этого метода состоит в следующем: 1) формулируются входное и выходное высказывания: входное высказывание описывает все необходимые входные условия для программы (или программного фрагмента), выходное высказывание описывает ожидаемый результат; 2) предполагая истинным входное высказывание, строится промежуточное высказывание, которое выводится на основании семантики операторов, расположенных между входом и выходом (входным и выходным высказываниями); такое высказывание называется выведенным высказыванием; 3) формулируется теорема (условия верификации): из выведенного высказывания следует выходное высказывание; 4) доказывается теорема; доказательство свидетельствует о правильности программы (программного фрагмента). Доказательство проводится при помощи хорошо разработанных математических методов, использующих исчисление предикатов первого порядка.
Условия верификации можно построить и в обратном направлении, т.е., считая истинным выходное высказывание, получить входное высказывание и доказывать теорему: из входного высказывания следует выведенное высказывание. Такой метод построения условий верификации моделирует выполнение программы в обратном направлении.
Другими словами, условия верификации должны отвечать на такой вопрос: если некоторое высказывание истинно после выполнения оператора программы, то, какое высказывание должно быть истинным перед оператором? Построение индуктивных высказываний помогает формализовать интуитивные представления о логике программы.
Оно и является самым сложным в процессе доказательства правильности программы. Это объясняется, во-первых, тем, что необходимо описать все содержательные условия, и, во-вторых, тем, что необходимо аксиоматическое описание семантики языка программирования.
Важным шагом в процессе доказательства является доказательство завершения выполнения программы, для чего бывает достаточно неформальных рассуждений. Таким образом, алгоритм доказательства правильности программы методом индуктивных высказываний представляется в следующем виде: 1) Построить структуру программы. 2) Выписать входное и выходное высказывания.
3) Сформулировать для всех циклов индуктивные высказывания. 4) Составить список выделенных путей. 5) Построить условия верификации. 6) Доказать условие верификации. 7) Доказать, что выполнение программы закончится. Этот метод сравним с обычным процессом чтения текста программы (метод сквозного контроля).
Различие заключается в степени формализации. Преимущество верификации состоит в том, что процесс доказательства настолько формализуем, что он может выполняться на вычислительной машине. В этом направлении в восьмидесятые годы проводились исследования, даже создавались автоматизированные диалоговые системы, но они не нашли практического применения.
Для автоматизированной диалоговой системы программист должен задать индуктивные высказывания на языке исчисления предикатов. Синтаксис и семантика языка программирования должны храниться в системе в виде аксиом на языке исчисления предикатов. Система должна определять пути в программе и строить условия верификации.
Основной компонент доказывающей системы — это построитель условий верификации, содержащий операции манипулирования предикатами, алгоритмы интерпретации операторов программы. Вторым компонентом системы является подсистема доказательства теорем. Отметим трудности, связанные с методом индуктивных высказываний.
Повторим, что трудно построить «множество основных аксиом, достаточно ограниченное для того, чтобы избежать противоречий, но достаточно богатое для того, чтобы служить отправной точкой для доказательства высказываний о программах». Вторая трудность — семантическая, заключающаяся в формировании самих высказываний, подлежащих доказательству. Если задача, для которой пишется программа, не имеет строгого математического описания, то для нее сложнее сформулировать условия верификации. Перечисленные методы имеют одно общее свойство: они рассматривают программу как уже существующий объект и затем доказывают ее правильность. Метод, который сформулировали К. Хоар и Э. Дейкстра основан на формальном выводе программ из математической постановки задачи.
01.04.2015 4.9 Mб 3 Тепляков — 11 000 БУХГАЛТЕРСКИХ ПРОВОДОК.rtf
Ограничение
Для продолжения скачивания необходимо пройти капчу:
Источник: studfile.net
Частичное доказательство правильности алгоритмов
Роберт Андерсон подчеркивает: «целью многих исследований в области доказательства правильности программ является. механизация таких доказательств» [66]. Дэвид Грис указывает, что «доказательство должно опережать построение программы» [67].
Объединив оба требования, получим, что автоматическое доказательство правильности должно опережать построение алгоритма. Нетрудно убедиться, что метод исчисления икон обеспечивает частичное выполнение этого требования.
Из математической логики известно, что логический вывод позволяет применить к аксиомам правила вывода и получить строго доказанные теоремы. Визуальный логический вывод, следуя этой схеме, берет за основу две визуальных аксиомы языка ДРАКОН (аксиому-силуэт и аксиому-примитив). Применяя к ним визуальные правила вывода, получим шампур-схему, т. е. графический каркас дракон-алгоритма.
Презентация на тему Доказательство правильности программ. Структурное программирование
Пример использования структурного программирования Структу́рное программи́рование — методология разработки программного обеспечения, в основе которой лежит представление программы в виде иерархической структуры блоков. Предложена в 1970-х годах Э. Дейкстрой Структурное программирование: Проектирование сверху вниз Функциональное
- Главная
- Информатика
- Доказательство правильности программ. Структурное программирование
Слайды и текст этой презентации
Слайд 1Доказательство правильности программ
Структурное программирование

Слайд 2Пример использования структурного программирования
Структу́рное программи́рование — методология
разработки программного
обеспечения, в основе которой лежит представление программы
в виде
иерархической структуры блоков. Предложена в 1970-х годах Э. Дейкстрой
Структурное программирование:
Проектирование сверху вниз
Функциональное программирование
Структурное кодирование
Задача нахождения НОД.
I. Общая постановка: даны целые a и b, найти их НОД.
Пусть a и b ≠ 0 и есть НОД(a,b). Ноль делится на любое число, поэтому НОД(0, 0) = 0 и
НОД(u, v) = НОД(v, u) и
НОД(u, v) = НОД (-u, v) и
НОД(u, 0) = u
II. Даны целые, неотрицательные a и b, найти их НОД.
Проведем декомпозицию этой задачи. Предположим, что можно привести задачу нахождения НОД(a,b) для b > 0, к задаче нахождения НОД(x,y), где x и y тоже неотрицательные и y
Слайд 3Пример использования структурного программирования
Декомпозиция на
три подзадачи:
положить x = a и y
= b
если y ≠ 0, то а) уменьшить y и изменить x так, чтобы x и y оставались >= 0, и чтобы значение НОД(x,y) оставалось тем же. b) повторить второй этап
если y = 0, положить НОД(a,b) = x
Первая и третья задача уже достаточно просты, а вторая …решена Евклидом:
III. Если (x div y) – целая часть, а (x mod y) – остаток, то x = (x div y) * y + (x mod y)
и если x и y делятся на какое-то число, то на это число будет делиться y и x – (x div y) * y, то есть y и (x mod y)
и НОД(x, y) = НОД(y, x mod y),
так как (x mod y)
Слайд 4
Пример использования структурного программирования
В исходной постановке задачи
только входные данные a и b, мы
ввели в рассмотрение три переменные: x, y и r >= 0 …..
Представим этапы проектирования блок-схемами…
1. — a>0, b>=0 2. — a>0, b>=0
Найти НОД(a, b) положить x = a и y = b
—НОД(a, b) = x — НОД(a, b)= НОД(x, y)
y ≠ 0 нет
НОД(a, b)= НОД(x, y) —
да — НОД(a, b) = x
уменьшить Y и изменить x
с сохранением НОД

Слайд 5
Пример использования структурного программирования
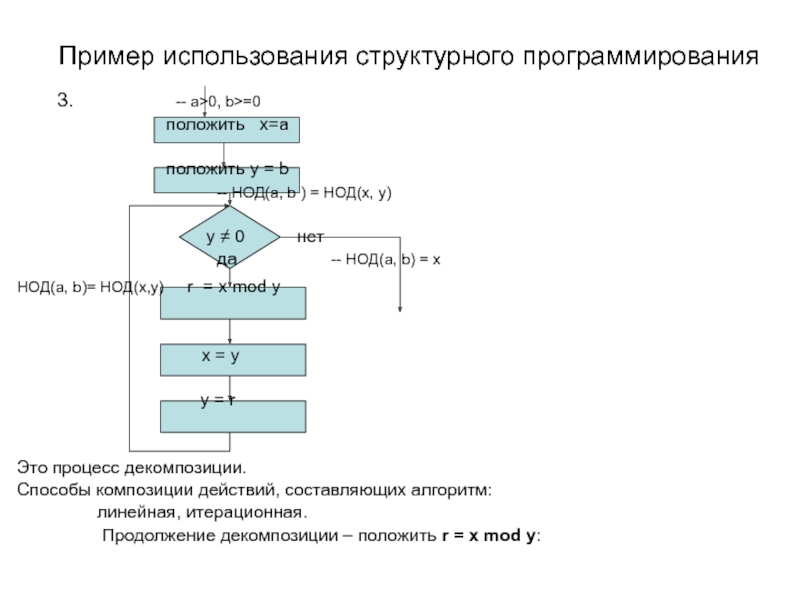
3.
— a>0, b>=0
положить y = b
— НОД(a, b ) = НОД(x, y)
y ≠ 0 нет
да — НОД(a, b) = x
НОД(a, b)= НОД(x,y) r = x mod y
Это процесс декомпозиции.
Способы композиции действий, составляющих алгоритм:
линейная, итерационная.
Продолжение декомпозиции – положить r = x mod y:
Слайд 6
Получение целой части и остатка отделения
—x ≥ 0, y
> 0
положить q = 0
положить r =x
— x = q*y + r, r ≥ 0
r ≥ y нет
x = q*r + y, r ≥ 0— да x = q*y+r, r ≥y —x = q*y+r, 0 ≤ r
Слайд 7Статическая и динамическая структура программы
Каждый алгоритм имеет
статическую и динамическую структуру.
Статическая структура представляется текстом
программы или его
структурной схемой, описывающими действия и проверки, которые
должны быть выполнены для решения конкретной задачи.
Статическая структура, текст не зависит от исходных данных.
Динамическая структура отражает процесс вычислений и
представляет собой последовательность состояний вычислений.
ДС зависит, определяется набором исходных данных, так как от
них зависит последовательность вычислений и переходов в
программе. Текущее состояние вычислений включает в себя
значения всех программных переменных в данный момент
времени и зависит от входных данных и от предыдущих состояний
вычислений.

Слайд 8Спецификация программы и правила вывода
Любой оператор или
изменяет состояние вычислений… или анализирует и принимает
решение…
Любой язык программирования включает в себя некоторое количество простых операторов и методы объединения, композиции их в составные, структурные.
Задача: описать соотношения и правила вывода, которые позволят определить эффект воздействия простого оператора на состояние вычислений и выделить свойства составного оператора из свойств входящих в него простых операторов.
На структурной схеме нахождения div и mod определены состояния вычислений с помощью соотношений, которые должны выполняться для входных и промежуточных величин.
Фундаментальным свойством всех способов композиции является возможность объединения в одну сложную структурную схему с одним входом и одним выходом произвольного количества любых структурных схем.

Слайд 9
Спецификация программы и правила вывода
— P
Спецификация программы:
S
< P>S < Q >(1) -Q
Если соотношение P – истинно перед выполнением S, то после завершения выполнения S, будет истинно выражение Q. …
Если S — это программа, корректность которой мы должны установить, то необходимо доказать нотацию (1), где P – соотношение, которому должны удовлетворять входные данные, а Q – выходные.
Для задачи поиска div и mod:
Слайд 10Спецификация программы и правила вывода
Проектирование должно начинаться
с определения спецификации S , которой
должна удовлетворять проектируемая программа, при каких условиях она должна работать (предусловие P) и какие результаты должны быть получены, каким условиям должны удовлетворять выходные данные (постусловие Q).
Процесс проектирования сверху вниз определяет спецификации Si для компонент программы Si
Проектирование программы осуществляется одновременно с доказательством корректности этих спецификаций.

Слайд 11
Представим блок-схему этого алгоритма как композицию…..
x>=0,
Источник: thepresentation.ru