Наугад выбирают два числа из отрезка [0;1]. Найдите вероятность того, что их сумма заключена между 1/4 и 1.
Пусть два числа это ( x ) и ( y )
Рисуем два отрезка от 0 до 1, т.к из этих отрезков мы берем два числа, получим систему координат
Значит получаем некую область
Рисуем на координатной плоскости

Красная область – оттуда мы должны брать числа ( x ) и ( y ) , чтобы их сумма лежала в указанном отрезке
Нам нужно найти ее площадь и разделить на площадь большого квадрата (S=1)
Ее площадь равна из площадь большого прямоугольного треугольника вычитаем площадь маленького прямоугольного треугольника
Источник: gdz-larin.ru
ЕГЭ по информатике 2021 — Задание 17 (Пишем программу)

Massivy 2
Обновлённую статью по 17 заданию можете посмотреть здесь.
Привет! Сегодня поговорим о 17 задании из ЕГЭ по информатике нового образца 2021.
Это задание так же, как и предыдущее, решается на компьютере. Нужно составить программу на одном из доступных языков программирования при сдаче ЕГЭ по информатике.
Из отрезка [0;1] наудачу выбираются 3 числа. Какова вероятность того, что их сумма не будет превышат
You seem to be using an older version of Internet Explorer. This site requires Internet Explorer 8 or higher. Update your browser here today to fully enjoy all the marvels of this site.

0 Голосов 
Из отрезка [0;1] наудачу выбираются 3 числа. Какова вероятность того, что их сумма не будет превышать единицу?
Лучший ответ

1 Vote 
Решение: обозначим числа, которые мы будем выбирать как (x,y,z). Каждое из этих чисел будем откладывать на одноименной оси на отрезке [0;1]. Получаем, что выбранные три числа это точки в декартовой системе координат с координатами ((x,y,z)) и которые попадают в куб с длиной ребра равной 1.
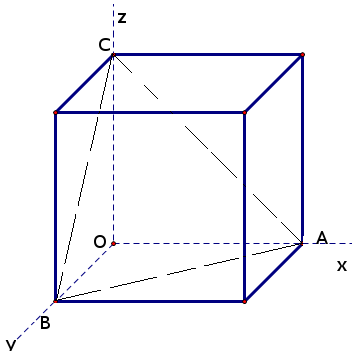
Согласно условия задачи мы должны найти вероятность для точек, для которых выполняется неравенство $$x+y+z leq 1$$
Найдем координаты точек, сумма координат которых не превышает единицу.
Рассмотрим некоторые ключевые точки:
A если координаты (y=z=0), ко координата (x leq 1), получаем координаты вершины (A(1,0,0))
B если координаты (x=z=0), ко координата (y leq 1), получаем координаты вершины (B(0,1,0))
Теория вероятностей | Математика TutorOnline
C если координаты (x=y=0), ко координата (z leq 1), получаем координаты вершины (C(0,0,1))
Рассмотрим плоскость, которая проходит через эти точки. Так как известны точки пересечения плоскости с осями, то уравнение этой плоскости в отрезках на осях равно $$ x+y+z = 1$$ а точки, сумма координат которых меньше 1, будут лежать ниже этой плоскости $$ x+y+z leq 1$$ Получили, что искомые точки — точки, принадлежащие пирамиде (OABC), тогда искомая вероятность будет равна отношению объемов пирамиды и куба $$P = frac>>$$ Объем куба равен (V_ =a^3), т.к. длина ребра равна (a=1 ) => (V_ = 1)
Объем пирамиды равен (V_ =fracS_H), т.к. в основании лежит прямоугольный равнобедренный треугольник, то (S_ = fraca^2), а (H=a=1), получаем (V_ =frac*fraca^2*a = fraca^3 = frac)
Вероятность того, что сумма чисел x,y,z будет не больше 1 равна $$P = frac>> = frac> = frac$$
Ответ: вероятность того, что сумма чисел (x+y+z leq 1) равна (P= frac)
- Задать вопрос
- Посмотреть мои вопросы
- Посмотреть Последние Вопросы
- Посмотреть все вопросы
Источник: seekland.info